6 Biomechanics
Mechanics is a branch of physics that is concerned with the motion and deformation of bodies that are acted on by mechanical forces. Mechanics is one of the oldest physical sciences dating back to Aristotle (384-322 bc) with his organized analysis of animal movement. Leonardo daVinci (1452-1519) worked on the mechanics of the human body, and his detailed anatomic sketches represent the birth of anatomy as a discipline and mechanics as the science governing human motion. Although daVinci wrote extensively on body mechanics, the man generally credited to be the father of modern biomechanics is Giovanni Alphonso Borelli (1608-1679). His book De motu Animalian provided a quantitative graphical solution to a musculoskeletal biomechanics problem (Figure 6-1).1
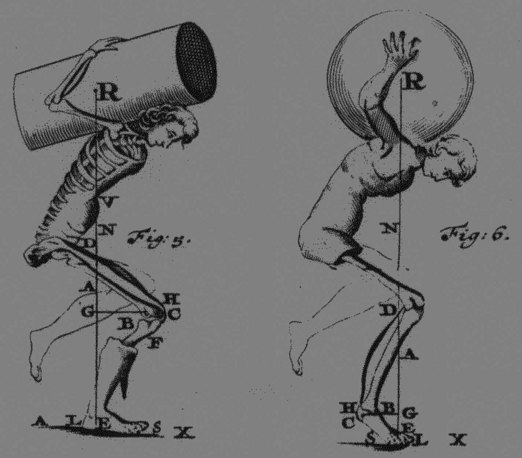
Figure 6-1 Borelli’s quantitative graphical solution to a musculoskeletal biomechanics problem.
(From Borelli GA: De motu animalium, Batavis, 1685, Lugduni.)
Kinematics
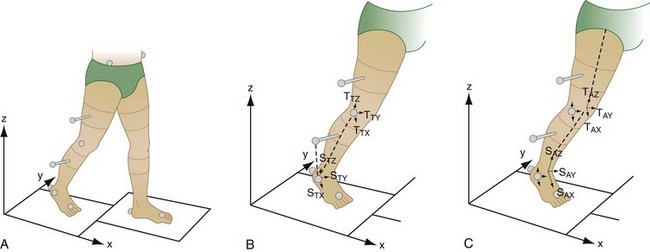
Kinematic techniques have been used to study body movements in both 2-D and 3-D space. The human body is typically modeled as a number of interconnected rigid body segments (Figure 6-2). A coordinate system is affixed to each rigid body segment in order to establish an anatomic coordinate system. External markers are used to define orthogonal coordinate systems whose axes define the position of these body segments. Joint motion is then described as the relative motion of the distal body segment with respect to the proximal body segment. Limb segments are assumed to undergo angular displacement during human movement. However, more sophisticated analyses will also quantify the linear displacement that limb segments may undergo. These measures of relative segmental angles have been used to describe human walking and other activities of daily living.2–7
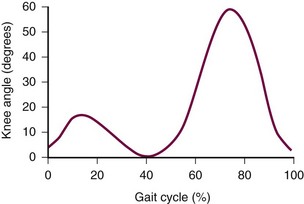
As an example, knee motion in the sagittal plane can be characterized throughout the gait cycle (Figure 6-3). At heel strike, the knee is nearly fully extended (knee flexion of 5 degrees). During midstance, the knee flexes to about 15 degrees, which occurs at 15% of the gait cycle. The knee joint is brought back into extension by midstance. At 50% of the gait cycle, opposite foot contact occurs. The weight is shifted to the opposite limb, and the knee begins flexing. Toe-off occurs at 60% of the gait cycle. Peak knee flexion of 60 degrees occurs during the swing phase. The knee motion can be described as two flexion waves, each starting in relative extension, progressing into flexion, then returning again to extension. The first flexion wave, or stance phase knee flexion, acts as a shock absorber to aid weight acceptance. This curve peaks in early stance at opposite foot-off. The mechanical source for this shock absorber is the eccentrically contracting quadriceps muscles. The second flexion wave is necessary in order to clear the foot in early swing phase. The knee is rapidly flexed beginning just after heel rise to a maximum in swing phase just as the swinging foot passes the opposite limb.
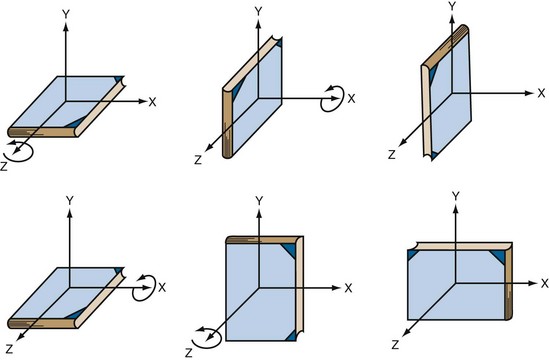
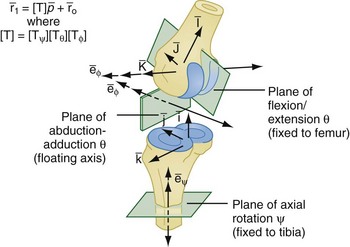
The complexity of kinematic analysis increases substantially when going from planar analysis to 3-D analysis. The complexity of the analysis arises from the technical difficulty that large rigid body rotations cannot be treated as vectors and, hence, do not obey the vectorial principles of transformation, independence, and interchangeability of operations. For finite spatial rotation, the sequence of rotations is extremely important and must be specified for a unique description of joint motion.8,9 For the same amount of rotation, different final orientations will result from different sequences of rotation (Figure 6-4). However, with proper selection and definition of the axes of rotation between two bony segments, it is possible to make finite rotation sequence independent or communitive.8,9 The concept of Eulerian angles has been adopted in the field of orthopedic biomechanics to unify the definition of finite spatial rotation. In the selection of reference axes, one axis is fixed to the stationary segment and another axis is fixed to the moving segment (Figure 6-5). In the knee joint, for example, the flexion/extension angle, Φ, occurs about a medial-laterally directed axis defined by a line connecting the medial and lateral femoral condyles. The axial rotation angle, ψ, is measured about an axis defined by the line along the shaft of the tibia. The third axis, also defined as the floating axis, is orthogonal to the other two axes and defines abduction/adduction, Θ. These rotations match the Eulerian angle description and are thought to be performed in such a way as to bring the moving segment from the reference orientation into the current orientation. The advantage of using this system for description of the spatial rotation of anatomic joints is that the angular rotations do not have to be referred back to the neutral position of the joint because the rotation sequence can be independent. Thus the measurement can be easily obtained and related to anatomic structures.
A complete analysis of total joint movement (i.e., six degrees of freedom) can be obtained using markers embedded in the bone10,11 or dual fluoroscopic imaging techniques.12,13 This general unconstrained movement in 3-D space requires the description of three translations and three rotations to fully describe joint motion. The most commonly used analytic method for description of six degrees-of-freedom displacement of a rigid body is the screw displacement axis (SDA).14–16
Kinetics
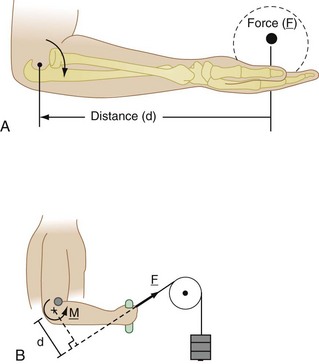
The key quantities in kinetics are force, moment, and torque. Forces represent an interaction between two bodies. Forces can be contact forces (bodies touching each other) or field forces (bodies separated by a distance, such as gravitational, electric, or magnetic forces). Forces are represented by vectors. Vectors are composed of four components: magnitude, direction, sense, and position (also called point of application). According to Newton’s Second Law, force is any action that tends to change the state of rest or state of motion of a body to which it is applied. Forces are represented by vectors. The vector may be resolved into several component forces, usually along specified mutually perpendicular coordinate axes. Conversely, forces can be summed using vectorial addition. A moment represents the turning, twisting, or rotational effect of a force. A moment is a vector. A moment is defined as the product of the force and the perpendicular distance between the line of action of the force and the axis of rotation of the motion that the force produces (Figure 6-6). Its magnitude is the force times the perpendicular distance to the axis of rotation. The direction of the moment is along the axis of rotation (or potential rotation) and thus perpendicular to the plane in which the twisting force is applied. The moment arm, the distance used to calculate the moment, is the shortest distance from the force action line to the actual or potential pivot point of the system, regardless of the state of motion. Skeletal motions are the result of moments applied by muscles that cross the joints on which they act. Moments of a force about an axis measure the tendency of the force to impart to the body a motion of rotation about a fixed axis. A torque is a special type of moment that results when a pair of forces that have equal magnitude, parallel lines of action, and opposite senses act on a body (Figure 6-7). The magnitude of the torque is Fd, where d is the perpendicular distance between the two forces. The resultant force is zero because the two forces are equal and oppose each other.
< div class='tao-gold-member'>
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree