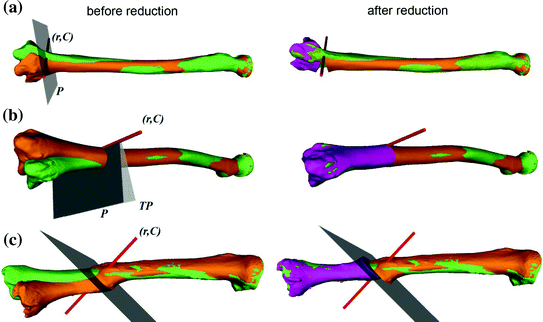
Fig. 1
Template-based planning approach demonstrated for the radius bone. a Pathological radius (orange) and mirrored, contralateral bone (green) serving as the reconstruction template. b Aligning the proximal part (orange) to the goal model reveals the deformity (violet). c The reduction is simulated by subsequently aligning the distal part. The relative transformation T between the proximal and distal bone parts quantifies the amount of reduction (Color figure online)
During this planning stage, potential side-to-side differences between the bones must also be identified and compensated because several studies showed that asymmetry between the left and the right limbs exist for long bones [39–41] such as in length and torsion. Asymmetry in size can be compensated easier for anatomy where the joint is formed by two bones (forearm: radius and ulna; lower leg: tibia and fibula). In such cases, the normal bones of both sides are compared to determine the size differences as demonstrated in Fig. 2. Thereafter, the goal model is first scaled by the same amount before its registration with the pathological bone.


Fig. 2
Compensation of length differences shown for the forearm bones radius and ulna. The normal ulna from the pathological side (pathological radius not shown) is denoted by orange color. The contralateral forearm bones are shown in yellow. The ulnae of both sides are compared to assess the length differences 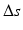 between the left and right forearm. The contralateral radius is scaled by
between the left and right forearm. The contralateral radius is scaled by 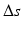 , resulting in the goal model (green bone) used as the reconstruction template (Color figure online)
, resulting in the goal model (green bone) used as the reconstruction template (Color figure online)
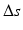 between the left and right forearm. The contralateral radius is scaled by
between the left and right forearm. The contralateral radius is scaled by 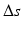 , resulting in the goal model (green bone) used as the reconstruction template (Color figure online)
, resulting in the goal model (green bone) used as the reconstruction template (Color figure online)A computer-planned corrective osteotomy does not involve only determining the optimal reduction, but also additional clinical factors crucial for a successful outcome shall be considered and optimized. After preliminary alignment, the surgeon is able to specify these parameters and constraints; e.g., possible access to the bone, osteotomy site, and type of the implant. Based on such specifications, the optimal surgical parameter values are determined in the planning tool: Besides the correction amount, the optimal selection of the osteotomy type, the position/orientation of the cutting plane(s), and the implant/screws position are important for a successful outcome and subsequent bone healing process.
A fundamental rule of conventional orthopedic planning is that a malunited bone is ideally cut at the apex of the deformity, which is the center of rotational angulation (CORA) [13] or the point of maximal deformity [7]. However, in practice a malunion has to be always regarded as a 3D deformity with 6 DoF to correct, hence restoring the normal anatomy requires one rotation—around a 3D axis often oblique to the anatomical standard planes—and one additional translation along a 3D displacement vector. While the direction r of the rotation axis can be calculated from the rotation matrix 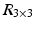 of T [42], the center of rotation, C, can be chosen arbitrarily if no additional constraints are introduced. From the clinical point of view, it is desirable to choose the osteotomy site such that the fragments are minimally displaced after reduction to avoid creating gaps or steps at the osteotomy site. This can be achieved if C is close to the osteotomy site, on the one hand, and if C is only minimally translated after applying T, on the other hand. The latter holds true if
of T [42], the center of rotation, C, can be chosen arbitrarily if no additional constraints are introduced. From the clinical point of view, it is desirable to choose the osteotomy site such that the fragments are minimally displaced after reduction to avoid creating gaps or steps at the osteotomy site. This can be achieved if C is close to the osteotomy site, on the one hand, and if C is only minimally translated after applying T, on the other hand. The latter holds true if 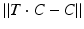 is minimal. Decomposition of T yields the ill-posed minimization problem
is minimal. Decomposition of T yields the ill-posed minimization problem 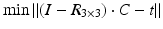 , where t denotes the translational component of T. Further constraints can be introduced since any point on the desired axis would be a valid solution of the equation system
, where t denotes the translational component of T. Further constraints can be introduced since any point on the desired axis would be a valid solution of the equation system 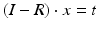 . Additionally defining C as the point on the axis being closest to a reference point p r (e.g., the center of the bone model) yields the equation with a unique solution
. Additionally defining C as the point on the axis being closest to a reference point p r (e.g., the center of the bone model) yields the equation with a unique solution
![$$\left( {\begin{array}{*{20}c} {I - R} \\ r \\ \end{array} } \right) \cdot x = \left( {\begin{array}{*{20}c} t \\ { < p_{r } ,r > } \\ \end{array} } \right)$$” src=”/wp-content/uploads/2016/09/A331438_1_En_7_Chapter_Equa.gif”></DIV></DIV></DIV>where the < > operator denotes the inner product. The resulting axis (<SPAN class=EmphasisTypeItalic>r</SPAN>, <SPAN class=EmphasisTypeItalic>C</SPAN>) can be visualized in the planning application indicating the osteotomy position as demonstrated in Fig. <SPAN class=InternalRef><A href=]() 3.
3.
Get Clinical Tree app for offline access

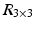 of T [42], the center of rotation, C, can be chosen arbitrarily if no additional constraints are introduced. From the clinical point of view, it is desirable to choose the osteotomy site such that the fragments are minimally displaced after reduction to avoid creating gaps or steps at the osteotomy site. This can be achieved if C is close to the osteotomy site, on the one hand, and if C is only minimally translated after applying T, on the other hand. The latter holds true if
of T [42], the center of rotation, C, can be chosen arbitrarily if no additional constraints are introduced. From the clinical point of view, it is desirable to choose the osteotomy site such that the fragments are minimally displaced after reduction to avoid creating gaps or steps at the osteotomy site. This can be achieved if C is close to the osteotomy site, on the one hand, and if C is only minimally translated after applying T, on the other hand. The latter holds true if 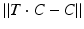 is minimal. Decomposition of T yields the ill-posed minimization problem
is minimal. Decomposition of T yields the ill-posed minimization problem 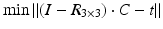 , where t denotes the translational component of T. Further constraints can be introduced since any point on the desired axis would be a valid solution of the equation system
, where t denotes the translational component of T. Further constraints can be introduced since any point on the desired axis would be a valid solution of the equation system 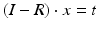 . Additionally defining C as the point on the axis being closest to a reference point p r (e.g., the center of the bone model) yields the equation with a unique solution
. Additionally defining C as the point on the axis being closest to a reference point p r (e.g., the center of the bone model) yields the equation with a unique solution
Fig. 3
Different types of osteotomies planned in 3D. The rotation axis (r, C) and the osteotomy plane(s) are shown in red and grey, respectively. The pathological (orange) and contralateral bone (green) are given before (first column) and after (second column) simulated reduction. The reduced bone fragment is depicted in violet. a Distal radius opening wedge osteotomy. b Closing wedge osteotomy of the radius. c Single cut osteotomy of the tibia (Color figure online)
The type of osteotomy and the orientation of the osteotomy plane directly influence how the bone surfaces will be in contact after reduction. Achieving maximum contact between the cortical bone layers of the fragments is strongly desired to promote healing. Again, the previously calculated axis (r, C) can provide a starting point to improve such contact.
As demonstrated in Fig. 3, a closing or opening wedge osteotomy is indicated if angular deformity is predominant; i.e., if the direction r is considerable different from the direction of the bone long axis. Adding or removing a bone wedge is also indicated if shortening or lengthening of the bone is required, i.e., a translation along the bone length axis between the aligned bone fragments was assessed. Given the osteotomy plane P and transformation T, the wedge is defined by P and 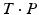 , where the line of intersection between the planes represents the hinge of the wedge. As demonstrated in Fig. 3b, so-called incomplete closing wedge osteotomies can be preoperatively planned if P is oriented such that the line of intersection coincides with (r, C) Incomplete osteotomies are often preferred for bones of the lower limb, promoting bone consolidation and early loading. In this procedure, the bone is not entirely cut but a small cortical bone bridge remains, almost constraining the reduction to a rotation around the bone bridge (i.e., the hinge of the wedge). Vice-versa, the preoperatively planned reduction can be only achieved if the hinge corresponds to (r, C). More examples of this osteotomy type will be given later in Sect. 2.2. Dependent on the position of the hinge, a situation may arise where the wedge type is not clearly defined; i.e., part of the bones overlap while also a gap is created. For such situations, CASPA permits the visualization of the wedge in real time by simultaneously rendering P and
, where the line of intersection between the planes represents the hinge of the wedge. As demonstrated in Fig. 3b, so-called incomplete closing wedge osteotomies can be preoperatively planned if P is oriented such that the line of intersection coincides with (r, C) Incomplete osteotomies are often preferred for bones of the lower limb, promoting bone consolidation and early loading. In this procedure, the bone is not entirely cut but a small cortical bone bridge remains, almost constraining the reduction to a rotation around the bone bridge (i.e., the hinge of the wedge). Vice-versa, the preoperatively planned reduction can be only achieved if the hinge corresponds to (r, C). More examples of this osteotomy type will be given later in Sect. 2.2. Dependent on the position of the hinge, a situation may arise where the wedge type is not clearly defined; i.e., part of the bones overlap while also a gap is created. For such situations, CASPA permits the visualization of the wedge in real time by simultaneously rendering P and 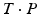 on display. By doing so, the osteotomy plane can be interactively translated until the desired wedge osteotomy can be achieved.
on display. By doing so, the osteotomy plane can be interactively translated until the desired wedge osteotomy can be achieved.
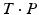 , where the line of intersection between the planes represents the hinge of the wedge. As demonstrated in Fig. 3b, so-called incomplete closing wedge osteotomies can be preoperatively planned if P is oriented such that the line of intersection coincides with (r, C) Incomplete osteotomies are often preferred for bones of the lower limb, promoting bone consolidation and early loading. In this procedure, the bone is not entirely cut but a small cortical bone bridge remains, almost constraining the reduction to a rotation around the bone bridge (i.e., the hinge of the wedge). Vice-versa, the preoperatively planned reduction can be only achieved if the hinge corresponds to (r, C). More examples of this osteotomy type will be given later in Sect. 2.2. Dependent on the position of the hinge, a situation may arise where the wedge type is not clearly defined; i.e., part of the bones overlap while also a gap is created. For such situations, CASPA permits the visualization of the wedge in real time by simultaneously rendering P and
, where the line of intersection between the planes represents the hinge of the wedge. As demonstrated in Fig. 3b, so-called incomplete closing wedge osteotomies can be preoperatively planned if P is oriented such that the line of intersection coincides with (r, C) Incomplete osteotomies are often preferred for bones of the lower limb, promoting bone consolidation and early loading. In this procedure, the bone is not entirely cut but a small cortical bone bridge remains, almost constraining the reduction to a rotation around the bone bridge (i.e., the hinge of the wedge). Vice-versa, the preoperatively planned reduction can be only achieved if the hinge corresponds to (r, C). More examples of this osteotomy type will be given later in Sect. 2.2. Dependent on the position of the hinge, a situation may arise where the wedge type is not clearly defined; i.e., part of the bones overlap while also a gap is created. For such situations, CASPA permits the visualization of the wedge in real time by simultaneously rendering P and 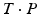 on display. By doing so, the osteotomy plane can be interactively translated until the desired wedge osteotomy can be achieved.
on display. By doing so, the osteotomy plane can be interactively translated until the desired wedge osteotomy can be achieved.If a rotational deformity is predominant, a so-called single cut osteotomy may be preferable to a wedge osteotomy. In this type of osteotomy, a single cut is performed which is pre-calculated such that sliding along and rotation in the cut plane permits reduction as planned [43]. An example of this osteotomy type is given in Fig. 3c. The position and orientation of a single cut osteotomy plane can be derived directly from the calculated reduction, i.e., the plane normal is defined by r. Although the single cut plane can be calculated exactly for any T, the osteotomy can be only applied if the translational component of T along the plane normal is negligible (i.e., below 1 mm) and the tangential translation is small, because otherwise either the bone contact surface would be too small or, worse, a gap between the bone parts would be created.
The inclusion of the osteosynthesis plate model, if available, into the preoperative plan, as demonstrated in Fig. 8a, can help to ensure a proper fitting of the plate. A poor plate fitting may result in less controlled procedure and decreased stability, which may lead to inaccurate reduction, delayed or stalled bone healing, or even implant failure. Inappropriately placed screws are another cause of delayed consolidation, and they may also harm the surrounding soft tissue. The best-fitting implant type can indeed be easily determined in the planning tool and also the optimal position of such implant can already be defined preoperatively. Optimally, the implant also contains the position and direction of the screws. The screw models are used by the surgeon to verify that all screws will be placed sufficiently inside the bone but without penetrating the osteotomy plane or anatomical regions at risk.
In severe deformities, one osteotomy may not be sufficient to achieve a satisfactory result. In such cases, multiple mutually-dependent osteotomies must be performed, resulting in a considerable increase in the complexity of the preoperative plan. As demonstrated in the example case given in Fig. 4, we propose a step-wise approach in such cases. The 14-years-old patient suffered from a posttraumatic malunion of both forearm bones, resulting from a fall four years ago. The deformity was assessed by aligning the distal third of each pathological bone to the contralateral model using ICP (Fig. 4a). Next, mid-shaft osteotomies at the apex of the deformity were performed for both radius and ulna, and the reduction was simulated by registering the proximal parts to the goal models using ICP. As shown in Fig. 4b, the resulting reduction of the radius fragment was not acceptable from a clinical point of view, due to the large gap and cortical surface mismatch on the radius. Therefore, an additional osteotomy was defined in the distal third of the radius and the resulting fragment was manually aligned to the goal model. In a second iteration, the transformation between the bone fragments and the osteotomy sites were fine-tuned in a manual fashion in order to achieve correct aligment by applying only single-cut osteotomies. The final result, given in Fig. 4c, was obtained after recalculating the surgical plan.
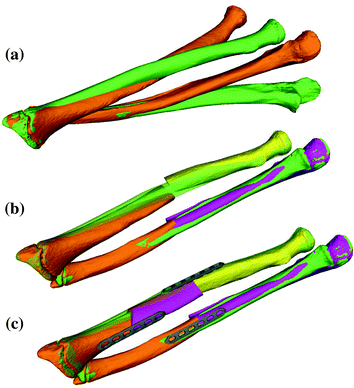

Fig. 4
Stepwise preoperative planning of a triple osteotomy for treating a complex deformity affecting both bones of the forearm. The reconstruction template is shown in green. a First step: radius and ulna were distally aligned to the template. b Second step: for both bones mid-shaft osteotomies were performed. c Third step: final result after an additional radius osteotomy (Color figure online)
2.2 Axis Realignment
Realignment of the lower limb is primarily indicated in patients having a varus- (out-knee) or valgus-deformity (in-knee), resulting in a pathologically deviated weight-bearing line of the leg (i.e., the mechanical axis) [13]. In many cases, the deformity is caused by a congenital defect affecting both limbs and, therefore, the contralateral bone cannot be used as a reconstruction template. Instead, the required correction is determined by realigning the mechanical axis to its anatomically normal position. According to Paley et al. [13], the mechanical leg axis passes not exactly through the knee joint center, but is located 8 ± 7 mm medial to the knee joint center. This deviation is called mechanical axis deviation (MAD) and is measured as the perpendicular distance from the mechanical leg axis to the knee joint center. A malalignment can be considered as pathological if the MAD lies outside of this normal range.
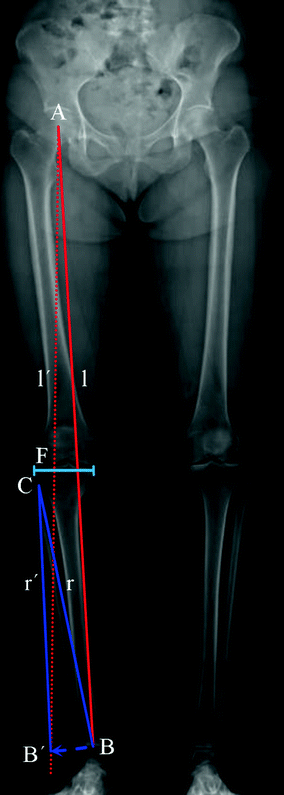
Before describing the 3D method for the preoperative planning of axis realignment procedures, the conventional approach is next briefly summarized. In the conventional preoperative assessment, long-leg standing X-rays are acquired for determining pathological and normal mechanical leg axes, as depicted in Fig. 5. Based on these axes, the position C and opening angle 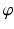 of a corrective osteotomy is calculated using a method described by Miniaci et al. [44]. In a first step, the preoperative mechanical leg axis l is determined as the straight line from the hip joint center A to the upper ankle joint center B. The postoperative axis
of a corrective osteotomy is calculated using a method described by Miniaci et al. [44]. In a first step, the preoperative mechanical leg axis l is determined as the straight line from the hip joint center A to the upper ankle joint center B. The postoperative axis 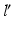 can be calculated by considering the fact that it should pass through a point F on the tibia plateau, at 62 % of the plateau width measured from medial (for varus-deformity). Point F is the so-called Fujisawa point, named after the author of the study [45], in which the optimal intersection point between the mechanical leg axis and the tibial plateau was investigated. The position of the rotation center of the osteotomy C is dependent on the pathology (e.g., closing/opening tibial/femur osteotomy). After the center of the osteotomy C is defined by the surgeon, the angle
can be calculated by considering the fact that it should pass through a point F on the tibia plateau, at 62 % of the plateau width measured from medial (for varus-deformity). Point F is the so-called Fujisawa point, named after the author of the study [45], in which the optimal intersection point between the mechanical leg axis and the tibial plateau was investigated. The position of the rotation center of the osteotomy C is dependent on the pathology (e.g., closing/opening tibial/femur osteotomy). After the center of the osteotomy C is defined by the surgeon, the angle 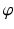 can be calculated. For this purpose, C is connected by the line r with the preoperative upper ankle joint center B. Lastly, the postoperative ankle joint center
can be calculated. For this purpose, C is connected by the line r with the preoperative upper ankle joint center B. Lastly, the postoperative ankle joint center 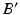 and, correspondingly, the osteotomy angle
and, correspondingly, the osteotomy angle 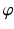 are determined by rotating r around C until it intersects with the postoperative axis
are determined by rotating r around C until it intersects with the postoperative axis 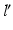 at point
at point 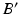 .
.
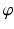 of a corrective osteotomy is calculated using a method described by Miniaci et al. [44]. In a first step, the preoperative mechanical leg axis l is determined as the straight line from the hip joint center A to the upper ankle joint center B. The postoperative axis
of a corrective osteotomy is calculated using a method described by Miniaci et al. [44]. In a first step, the preoperative mechanical leg axis l is determined as the straight line from the hip joint center A to the upper ankle joint center B. The postoperative axis 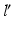 can be calculated by considering the fact that it should pass through a point F on the tibia plateau, at 62 % of the plateau width measured from medial (for varus-deformity). Point F is the so-called Fujisawa point, named after the author of the study [45], in which the optimal intersection point between the mechanical leg axis and the tibial plateau was investigated. The position of the rotation center of the osteotomy C is dependent on the pathology (e.g., closing/opening tibial/femur osteotomy). After the center of the osteotomy C is defined by the surgeon, the angle
can be calculated by considering the fact that it should pass through a point F on the tibia plateau, at 62 % of the plateau width measured from medial (for varus-deformity). Point F is the so-called Fujisawa point, named after the author of the study [45], in which the optimal intersection point between the mechanical leg axis and the tibial plateau was investigated. The position of the rotation center of the osteotomy C is dependent on the pathology (e.g., closing/opening tibial/femur osteotomy). After the center of the osteotomy C is defined by the surgeon, the angle 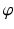 can be calculated. For this purpose, C is connected by the line r with the preoperative upper ankle joint center B. Lastly, the postoperative ankle joint center
can be calculated. For this purpose, C is connected by the line r with the preoperative upper ankle joint center B. Lastly, the postoperative ankle joint center 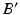 and, correspondingly, the osteotomy angle
and, correspondingly, the osteotomy angle 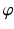 are determined by rotating r around C until it intersects with the postoperative axis
are determined by rotating r around C until it intersects with the postoperative axis 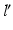 at point
at point 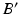 .
.
Fig. 5
Measurement of the pathological mechanical leg axis l and calculation of the realigned normal axis 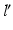 in 2D
in 2D
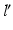 in 2D
in 2DWe have developed a method for quantifying the required 3D osteotomy parameters (i.e., position, rotation axis, and angle). Our approach requires having triangular surface models of the hip, knee, and ankle joints. We apply a CT protocol that scans the regions of interests while skipping the irrelevant mid-shaft regions to reduce radiation exposure. Based on the CT scan, a limb model consisting of the proximal femur, distal femur, patella, proximal tibia, distal tibia, distal fibula and talus, is reconstructed. Thereafter the hip, knee, and ankle joint centers of the limb model have to be determined in 3D before the mechanical axes can be calculated.
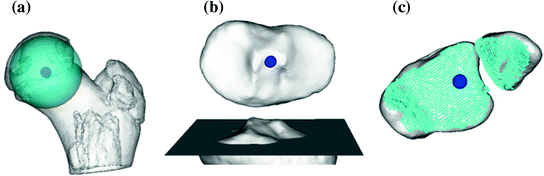
The joint center of the proximal femur A is defined by the center of the best fitting sphere [46], minimizing the distance to a user-selected region of the femoral head points, as demonstrated in Fig. 6a. The bone model of the proximal tibia is used to determine the center of the knee joint and an analytical description of the tibia plateau plane 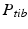 (Fig. 6b), both required for computing the Fujisawa point. We follow Moreland [47] who defined the knee joint center as the midpoint between the intercondylar eminences of the tibial plateau. As for the femur, a least squares approach is applied for finding the plane
(Fig. 6b), both required for computing the Fujisawa point. We follow Moreland [47] who defined the knee joint center as the midpoint between the intercondylar eminences of the tibial plateau. As for the femur, a least squares approach is applied for finding the plane 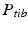 , minimizing the distance to user-selected plateau regions as depicted in Fig. 6b. Lastly, the center of ankle joint B is calculated as demonstrated in Fig. 6c. The ankle center can be anatomically described as the midpoint between the medial and lateral malleolus [47], i.e., the center of the articular surface of both tibia and fibula with respect to the talus bone. Accordingly, we propose a method for calculating the 3D ankle joint center by analyzing the opposing articular surfaces between these bones. First, tibia and fibula points having a small distance to the talus bone are identified, because they are potential candidates for being articular surface points. These candidate points are efficiently found by calculating the closest-point distance to the talus bone model using a KD-tree [38] and considering only points below a user-defined distance threshold. A second criterion is introduced to eliminate false positive candidate points: All candidates, for which the angle between its surface normal vector and the direction vector to its closest point on the talus surface is above a user-defined threshold, are eliminated. Both thresholds are visually determined per case until the entire articular surface is detected as shown in Fig. 6c. Typically the distance and angle thresholds are between 4–8 mm and 40°–70°, respectively. The joint center is finally computed as the center of mass of all selected points on the tibia and fibula surface.
, minimizing the distance to user-selected plateau regions as depicted in Fig. 6b. Lastly, the center of ankle joint B is calculated as demonstrated in Fig. 6c. The ankle center can be anatomically described as the midpoint between the medial and lateral malleolus [47], i.e., the center of the articular surface of both tibia and fibula with respect to the talus bone. Accordingly, we propose a method for calculating the 3D ankle joint center by analyzing the opposing articular surfaces between these bones. First, tibia and fibula points having a small distance to the talus bone are identified, because they are potential candidates for being articular surface points. These candidate points are efficiently found by calculating the closest-point distance to the talus bone model using a KD-tree [38] and considering only points below a user-defined distance threshold. A second criterion is introduced to eliminate false positive candidate points: All candidates, for which the angle between its surface normal vector and the direction vector to its closest point on the talus surface is above a user-defined threshold, are eliminated. Both thresholds are visually determined per case until the entire articular surface is detected as shown in Fig. 6c. Typically the distance and angle thresholds are between 4–8 mm and 40°–70°, respectively. The joint center is finally computed as the center of mass of all selected points on the tibia and fibula surface.
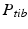 (Fig. 6b), both required for computing the Fujisawa point. We follow Moreland [47] who defined the knee joint center as the midpoint between the intercondylar eminences of the tibial plateau. As for the femur, a least squares approach is applied for finding the plane
(Fig. 6b), both required for computing the Fujisawa point. We follow Moreland [47] who defined the knee joint center as the midpoint between the intercondylar eminences of the tibial plateau. As for the femur, a least squares approach is applied for finding the plane 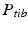 , minimizing the distance to user-selected plateau regions as depicted in Fig. 6b. Lastly, the center of ankle joint B is calculated as demonstrated in Fig. 6c. The ankle center can be anatomically described as the midpoint between the medial and lateral malleolus [47], i.e., the center of the articular surface of both tibia and fibula with respect to the talus bone. Accordingly, we propose a method for calculating the 3D ankle joint center by analyzing the opposing articular surfaces between these bones. First, tibia and fibula points having a small distance to the talus bone are identified, because they are potential candidates for being articular surface points. These candidate points are efficiently found by calculating the closest-point distance to the talus bone model using a KD-tree [38] and considering only points below a user-defined distance threshold. A second criterion is introduced to eliminate false positive candidate points: All candidates, for which the angle between its surface normal vector and the direction vector to its closest point on the talus surface is above a user-defined threshold, are eliminated. Both thresholds are visually determined per case until the entire articular surface is detected as shown in Fig. 6c. Typically the distance and angle thresholds are between 4–8 mm and 40°–70°, respectively. The joint center is finally computed as the center of mass of all selected points on the tibia and fibula surface.
, minimizing the distance to user-selected plateau regions as depicted in Fig. 6b. Lastly, the center of ankle joint B is calculated as demonstrated in Fig. 6c. The ankle center can be anatomically described as the midpoint between the medial and lateral malleolus [47], i.e., the center of the articular surface of both tibia and fibula with respect to the talus bone. Accordingly, we propose a method for calculating the 3D ankle joint center by analyzing the opposing articular surfaces between these bones. First, tibia and fibula points having a small distance to the talus bone are identified, because they are potential candidates for being articular surface points. These candidate points are efficiently found by calculating the closest-point distance to the talus bone model using a KD-tree [38] and considering only points below a user-defined distance threshold. A second criterion is introduced to eliminate false positive candidate points: All candidates, for which the angle between its surface normal vector and the direction vector to its closest point on the talus surface is above a user-defined threshold, are eliminated. Both thresholds are visually determined per case until the entire articular surface is detected as shown in Fig. 6c. Typically the distance and angle thresholds are between 4–8 mm and 40°–70°, respectively. The joint center is finally computed as the center of mass of all selected points on the tibia and fibula surface.
Fig. 6
Determination of the relevant joint parameters. a The center of the femoral head is calculated by the center (dark blue) of the best fitting sphere (cyan). b Knee joint center (dark blue) and tibia plateau plane 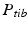 (dark grey). c The ankle joint center (dark blue) is defined as the center of mass of the articular surface (cyan points) (Color figure online)
(dark grey). c The ankle joint center (dark blue) is defined as the center of mass of the articular surface (cyan points) (Color figure online)
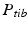 (dark grey). c The ankle joint center (dark blue) is defined as the center of mass of the articular surface (cyan points) (Color figure online)
(dark grey). c The ankle joint center (dark blue) is defined as the center of mass of the articular surface (cyan points) (Color figure online)After the joint centers are calculated, the pathological and corrected mechanical axes l and 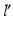 can be calculated in 3D (Fig. 7a–c). As depicted in Fig. 7b, axis l is defined as a straight line from the hip joint center A to the ankle joint center B. Axis
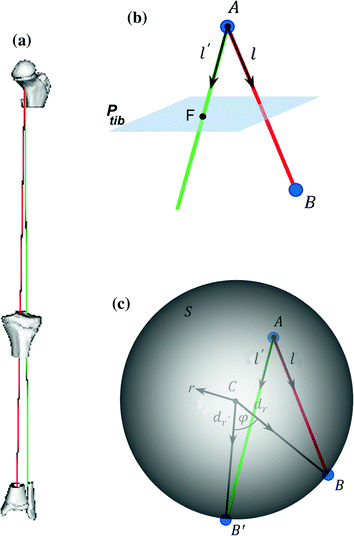
can be calculated in 3D (Fig. 7a–c). As depicted in Fig. 7b, axis l is defined as a straight line from the hip joint center A to the ankle joint center B. Axis 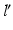 is defined by the direction vector from A, passing through the Fujisawa point F on
is defined by the direction vector from A, passing through the Fujisawa point F on 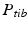 . For performing the desired correction, the osteotomy axis r must be perpendicular to the plane of deformity spanned by l and
. For performing the desired correction, the osteotomy axis r must be perpendicular to the plane of deformity spanned by l and 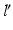 ; i.e.,
; i.e., 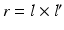 . The postoperative ankle joint center
. The postoperative ankle joint center 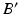 and the osteotomy angle
and the osteotomy angle 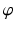 can be calculated by solving the line/sphere intersection problem shown in Fig. 7c. That is, since the length of the leg axis should not change,
can be calculated by solving the line/sphere intersection problem shown in Fig. 7c. That is, since the length of the leg axis should not change, 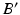 is located on the sphere S with the center C and radius
is located on the sphere S with the center C and radius 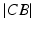 , i.e. at the intersection of axis
, i.e. at the intersection of axis 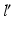 with S. Once
with S. Once 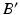 is determined, the osteotomy angle
is determined, the osteotomy angle 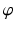 is computed from the angle between the direction vectors
is computed from the angle between the direction vectors 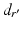 and
and 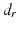 (Fig. 7c).
(Fig. 7c).
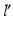 can be calculated in 3D (Fig. 7a–c). As depicted in Fig. 7b, axis l is defined as a straight line from the hip joint center A to the ankle joint center B. Axis
can be calculated in 3D (Fig. 7a–c). As depicted in Fig. 7b, axis l is defined as a straight line from the hip joint center A to the ankle joint center B. Axis 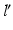 is defined by the direction vector from A, passing through the Fujisawa point F on
is defined by the direction vector from A, passing through the Fujisawa point F on 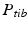 . For performing the desired correction, the osteotomy axis r must be perpendicular to the plane of deformity spanned by l and
. For performing the desired correction, the osteotomy axis r must be perpendicular to the plane of deformity spanned by l and 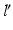 ; i.e.,
; i.e., 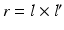 . The postoperative ankle joint center
. The postoperative ankle joint center 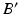 and the osteotomy angle
and the osteotomy angle 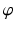 can be calculated by solving the line/sphere intersection problem shown in Fig. 7c. That is, since the length of the leg axis should not change,
can be calculated by solving the line/sphere intersection problem shown in Fig. 7c. That is, since the length of the leg axis should not change, 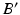 is located on the sphere S with the center C and radius
is located on the sphere S with the center C and radius 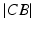 , i.e. at the intersection of axis
, i.e. at the intersection of axis 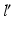 with S. Once
with S. Once 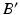 is determined, the osteotomy angle
is determined, the osteotomy angle 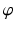 is computed from the angle between the direction vectors
is computed from the angle between the direction vectors 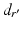 and
and 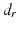 (Fig. 7c).
(Fig. 7c).
Fig. 7




Measurement of the pathological mechanical leg axis l and calculation of the realigned normal axis 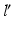 in 3D. a Mechanical leg axis before (red) and after (green) realignment. b Calculation of the Fujisawa point F for determining the direction of the postoperative leg axis
in 3D. a Mechanical leg axis before (red) and after (green) realignment. b Calculation of the Fujisawa point F for determining the direction of the postoperative leg axis 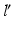 . c Calculation of the postoperative ankle joint center
. c Calculation of the postoperative ankle joint center 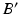 (Color figure online)
(Color figure online)
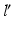 in 3D. a Mechanical leg axis before (red) and after (green) realignment. b Calculation of the Fujisawa point F for determining the direction of the postoperative leg axis
in 3D. a Mechanical leg axis before (red) and after (green) realignment. b Calculation of the Fujisawa point F for determining the direction of the postoperative leg axis 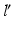 . c Calculation of the postoperative ankle joint center
. c Calculation of the postoperative ankle joint center 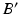 (Color figure online)
(Color figure online)Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








