Fig. 2.1
Schematic representations of the adult intervertebral disc. (a) Midsagittal cross section showing anatomical regions. (b) Three-dimensional view illustrating AF lamellar structure (Adapted from Smith et al. 2011)
The intervertebral disc undergoes biochemical and structural changes due to aging and degeneration. Biochemical changes include a decrease of proteoglycan content, an increase in protein cross-linking, and changes in the collagen type and distribution. The biochemical changes during degeneration are similar to those of aging; they are characterized by occurring in a faster rate and accompanied by structural changes that impair disc function. Structural changes observed during degeneration include a decrease in disc height, inward and outward bulging of the annulus fibrosus, and loss of its lamellar organization. The objective of this chapter is to describe the mechanical behavior of the individual tissues of the intervertebral disc and then analyze how they work together in different loading scenarios. In addition, the effects of degeneration on the mechanics at the tissue and disc levels are described.
2.2 Structure–Function of Intervertebral Disc Tissues
Although many studies have shed light on the structure–function relationships for the tissues that form the intervertebral disc, this is still an ongoing research topic, the aim of which is to describe the mechanical behavior of healthy tissues, the effects of degeneration, and the implications of disc mechanics on the cell biology. Recent findings on the structure–function relationships of the tissues of the intervertebral disc are presented in the following sections.
2.2.1 Osmotic Effects
The tissues of the intervertebral disc are mainly composed of water, proteoglycans, and collagen (Eyre 1979). The relative content of each of these components differs from tissue to tissue. For instance, the nucleus pulposus has the highest proteoglycan content, while the annulus fibrosus has the highest collagen content (see Chaps. 3 and 4) (Eyre and Muir 1976). The differences in relative content of these individual components and their organization provide these disc tissues with their special mechanical properties. For example, it is well known that due to its higher collagen content and fiber organization, the annulus fibrosus has a superior tensile loading capacity. In a similar way, the high proteoglycan content of the nucleus pulposus provides the tissue with high compressive properties. However, since the tissues in the disc have similar components, they also share some mechanical behaviors, specifically, the osmotic effects which reflect the proteoglycan high negative charge density (Urban and Maroudas 1981). The osmotic effects have important implications on the mechanics of the disc. For instance, the osmotic pressure causes a deformation of the tissue usually known as osmotic swelling. This swelling pressure induces tensile stresses and increases the stiffness of the tissue. This osmotic swelling also draws water into these tissues keeping the disc hydrated. Since the osmotic effects play an important role in the mechanics of all disc tissues, this section provides a brief description of the relationship between composition and osmotic effects.
The osmotic effects are mediated by the proteoglycan content of the tissue (Maroudas and Bannon 1981; Urban et al. 1979). Proteoglycans are large molecules composed of many glycosaminoglycan units attached to a long core protein. Glycosaminoglycans are chains of polysaccharides that at a physiological pH present an excess of negatively charged ions (Comper and Laurent 1978). The molecular structure of proteoglycans and glycosaminoglycans is discussed in great detail in Chap. 4. Due to their large size, proteoglycans are trapped in the network of collagen fibers. Therefore, collagen and proteoglycans form a charged, porous, deformable solid material which is embedded in a solution of water and ions (Urban and Maroudas 1981). The amount of negative charges attached to the solid is quantified by the fixed charge density. At equilibrium, the balance of chemical potentials results in an increase of osmotic pressure (p), which is a function of the fixed charge density and the ionic strength of the surrounding fluid (Overbeek 1956). Assuming an ideal solution for the interstitial fluid and external solution, the osmotic pressure can be expressed as
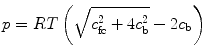
where R is the universal gas constant, T is the absolute temperature, c fc is the fixed charge density, and c b is osmolarity of the surrounding fluid bath.
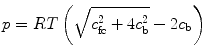
(1)
The osmotic pressure and the external applied forces result in deformation of the solid component of the tissue, which in turn alter the fixed charge density (c fc). That change can be quantified by
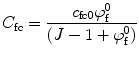
where 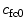 and
and 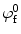 are the fixed charge density and the water content at the reference configuration, respectively, and J is the ratio between the volume at the deformed and reference configurations. The reference configuration, usually defined as the configuration where stresses are zero, plays an important role in the calculation of the osmotic pressure.
are the fixed charge density and the water content at the reference configuration, respectively, and J is the ratio between the volume at the deformed and reference configurations. The reference configuration, usually defined as the configuration where stresses are zero, plays an important role in the calculation of the osmotic pressure.
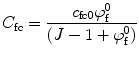
(2)
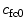 and
and 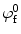 are the fixed charge density and the water content at the reference configuration, respectively, and J is the ratio between the volume at the deformed and reference configurations. The reference configuration, usually defined as the configuration where stresses are zero, plays an important role in the calculation of the osmotic pressure.
are the fixed charge density and the water content at the reference configuration, respectively, and J is the ratio between the volume at the deformed and reference configurations. The reference configuration, usually defined as the configuration where stresses are zero, plays an important role in the calculation of the osmotic pressure.2.2.2 Nucleus Pulposus
The nucleus pulposus is the gelatinous core of the intervertebral disc and it is composed of water (70–85 % of total weight), proteoglycans (30–50 % of dry weight), collagen (20 % of dry weight), and other minor proteins (Adams and Muir 1976; Eyre 1979). Aggrecan is the most abundant proteoglycan in the nucleus pulposus, followed by other proteoglycans such as decorin (Melrose et al. 2001). Aggrecan contains keratan and chondroitin sulfate chains which interact with hyaluronic acid filaments forming large molecules that are trapped in the collagen network (Kiani et al. 2002). These side chains are negatively charged; consequently, positively charged Na+ ions bind to these chains creating an accumulation of cations inside the nucleus pulposus. Since the glycosaminoglycans are not able to diffuse out of the nucleus pulposus, there is a permanent difference of the concentration of cations compared to the surrounding environment. This unbalance of cations is the cause of the osmotic pressure in the disc.
Collagen II is the most abundant type of collagen in the nucleus pulposus and other compression-bearing tissues such as articular cartilage (Eyre and Muir 1976). Unlike articular cartilage, collagen II forms an unorganized fiber network in the nucleus pulposus. A recent study showed that long fibers in the nucleus pulposus continuously connect both endplates (Wade et al. 2011). In an intact disc, these fibers are much longer than the disc height; they fold in a rather arbitrary configuration and can withstand substantial tension when unfolded. Experimentally, however, since it was necessary to cut the annulus fibrosus to separate the endplates, it is unlikely that the nucleus pulposus fibers experience high levels of tension under physiological conditions. This is different from articular cartilage, where fibers are highly organized and experience substantial tension due to the osmotic swelling (Ateshian et al. 2009; Cavalcante et al. 2005). In the case of the nucleus pulposus, the osmotic and hydrostatic pressure is supported axially by the endplates and radially by tensile (hoop) stresses in the annulus fibrosus. Consequently, fibers are not required to hold the nucleus pulposus in place as is the case in articular cartilage.
Due to its high levels of hydration and gelatinous consistency, the mechanical behavior of the nucleus pulposus has characteristics of both a fluid and a solid (Iatridis et al. 1996). Consequently, the nucleus pulposus is usually treated as a viscoelastic material. The mechanical properties of the nucleus pulposus have been investigated mainly through torsion and compression tests (Heneghan and Riches 2008a, b; Iatridis et al. 1997a, b; Johannessen and Elliott 2005; Perie et al. 2005). Confined compression has been typically used to measure several mechanical properties of the nucleus pulposus such as aggregate modulus and permeability coefficients (Johannessen and Elliott 2005). It is measured by axially compressing a cylindrical sample in a chamber that prevents lateral expansion. Although physiologically the nucleus pulposus is not fully confined or fully unconfined, confined compression tests have been generally accepted to characterize its compressive behavior. For small deformations (around 5 %), the nucleus pulposus can be considered to have a constant permeability and exhibits a linear relationship between stresses and strains (Johannessen and Elliott 2005). However, the properties are strain dependent (i.e., nonlinear) for moderate and large strains (Heneghan and Riches 2008a). Table 2.1 presents a summary of nucleus pulposus values obtained using confined compression.
Table 2.1
Aggregate modulus (H A) as a function of the stretch ratio (λ) and glycosaminoglycan content for the nucleus pulposus
Study | H A (kPa) | λ | NP tissue | s-GAG (% dry wt.) |
|---|---|---|---|---|
Heneghan andRiches (2008a) | 69–1,650 | 1.0–0.3 | Bovine tail | 24 |
Perie et al. (2005) | 350–520 | 1.0–0.8 | Bovine tail | |
Perie et al. (2006a) | ∼600 | 1.0–0.6 | Bovine tail | ∼35 |
Perie et al. (2006b) | ∼400–510 | 1.0–0.8 | Bovine tail | ∼42 |
Johannessen andElliott (2005) | 1,010 | 0.95 | Human | 44 |
The elastic behavior of the nucleus pulposus can be apportioned in terms of the contribution of osmotic (ionic) and solid tissue (nonionic) effects. The contribution of the osmotic effects to the compressive properties has been measured by eliminating the osmotic effects using a surrounding medium with high osmolarity or by reducing the proteoglycan content via enzymatic digestion (Heneghan and Riches 2008a; Perie et al. 2006b). When a high ionic concentration medium was used, the compressive properties of the bovine nucleus pulposus were reduced to 20–30 % of the value measured in isotonic (physiological) medium concentrations. Therefore, the contribution of the osmotic effects to the stiffness and load support of the nucleus pulposus is approximately 70–80 %. The contribution of the osmotic effects was almost constant through a wide range of applied deformations (0–70 % compressive strains). If the proteoglycans are removed by enzymatic digestion, a reduction of 20- to 30-fold was observed in the compressive properties of the nucleus pulposus (Perie et al. 2006b). This suggests that the proteoglycans also have a nonionic contribution to the mechanics of the nucleus pulposus. Evidence of the nonionic contribution of the proteoglycans has been reported for other tissues such as articular cartilage (Canal Guterl et al. 2010).
Viscoelastic or frequency-dependent properties of the nucleus pulposus have been analyzed using torsion tests (Iatridis et al. 1997a, b). Stress relaxation tests measured an instantaneous shear modulus around 11 kPa. However, the shear stress rapidly relaxed to near-zero values suggesting a fluid-like behavior. In dynamic torsion tests, a shear modulus of ∼20 kPa and a phase shift (the delay between strain and stress measured in terms of degrees) of ∼30° were measured. For comparison, the dynamic modulus of articular cartilage is 600–1,000 kPa, the modulus for the meniscus is 540 kPa, while proteoglycan solutions are 0.01 kPa (Hardingham et al. 1987; Zhu et al. 1993, 1994). Values of phase shift of 13° for cartilage, 22° for meniscus, and 65° for proteoglycan solutions have been reported. Since the phase shift for the nucleus is lower than 45°, it suggests a more solid-like dynamic behavior.
The studies discussed above illustrate the complexity of the mechanical behavior and structure–function relationships of the nucleus pulposus. The contribution of osmotic pressure and the blend between exhibiting characteristics of fluid and solid mechanics pose a difficult challenge to model and also complicate the prediction of deformations during physiological loading. Nonetheless, it is important to understand and characterize the mechanics of the nucleus pulposus as it influences cell function and impacts predictions related to mechanically induced injuries and regeneration.
2.2.3 Annulus Fibrosus
Similar to the nucleus pulposus, the annulus fibrosus is composed mainly of proteoglycans and collagen, although the relative content and organization of its components are substantially different. In the healthy human annulus fibrosus, the water content is 50 %, collagen is approximately 70 % of the dry weight, and proteoglycans make up to 10 % of the dry weight (Eyre and Muir 1976; Eyre 1979). The annulus fibrosus is subjected to both tensile and compressive stresses during physiological loading. Consequently, it has high collagen content similar to other tension-bearing tissues such as tendon and ligaments. Proceeding from the outer to the inner annulus, there is an decrease in the ratio of collagens I to II, and the amount of proteoglycan rises. This profile reflects a change in the loading environment from more tension in the outer annulus fibrosus to more compression towards the nucleus pulposus (Eyre and Muir 1976). In a similar way, in the outer annulus fibrosus, collagen fibers insert directly to the cortical bone of the vertebrae and not to the endplate as in the case of inner annulus fibrosus, again probably reflecting the higher tensile loads present in the outer annulus fibrosus (Nachemson 1963; Wu and Yao 1976).
Noteworthy, in the annulus, collagen fibers are arranged in concentric lamellae with alternating orientations (Fig. 2.1b). The angle between fiber directions of adjacent lamellae changes from ∼60° to the spinal axis in the outer annulus fibrosus to ∼90° in the inner annulus fibrosus (Cassidy et al. 1989; Guerin and Elliott 2006a; Hickey and Hukins 1980). This arrangement provides the annulus with a series of important mechanical properties, including anisotropy (direction dependence). Since the fibers play such an important role in the mechanics of the annulus fibrosus, this tissue can be analyzed as a combination of fibers and an isotropic material known as extrafibrillar matrix (Spencer 1984). As its name indicates, the extrafibrillar matrix represents all the solid components of the annulus fibrosus, except fibers.
One of the more important characteristics of the mechanics of collagenous tissues is nonlinearity. The nonlinearity of the fibers is characterized by a low stiffness region for small deformations, known as toe region, followed by a transition (heel) region and a much stiffer linear region (Guerin and Elliott 2007; Wu and Yao 1976). Collagen fibers, in most tension-bearing tissues, have a hierarchical organization from fibrils to large collagen bundles or fascicles (Kastelic et al. 1978). Collagen fibers in these tissues have a wavy or zigzag shape commonly known as crimp (Diamant et al. 1972; Kastelic and Baer 1980). When the fibers are stretched, the fibers progressively straighten with minimal resistance; i.e., a negligible force is required to uncrimp the fibers. The amount of stretch required to straighten the fiber is known as uncrimping stretch. Once a fiber is straight, it starts taking load (Fig. 2.2). The uncrimping stretch is not same for all fibers in a tissue. For small deformations, few fibers with a small uncrimping stretch are straightened as they accommodate the load. Consequently, the stiffness of the tissue is low. Progressively, all the fibers stretch and contribute to load support resulting in high tissue stiffness (Fig. 2.2). If the tissue is further stretched, fibers will fail by several possible mechanisms including breakage and fiber pullout.
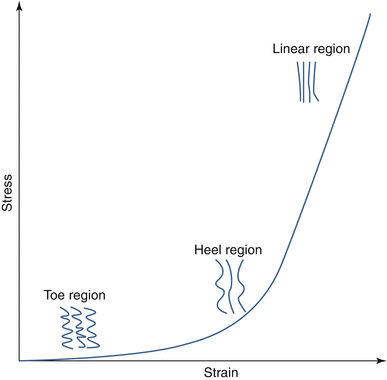

Fig. 2.2
The tensile stress–strain response of collagenous tissues, such as annulus fibrosus, can be divided into several regions, corresponding to different mechanisms. In the toe region, the contribution of fibers is small due to fiber crimping. In the heel region, the increase in stiffness is due to fiber straightening. In the linear region, most of the fibers are straight and contributing to the high tensile stiffness
All the other components of the annulus fibrosus (except the fibers) are usually treated as a single material known as extrafibrillar matrix. Since the fibers contribute to the mechanics of the annulus fibrosus when they are in tension, the matrix characterizes the compressive properties of the annulus fibrosus. Other properties, including permeability and diffusivity of solutes, are also attributed to matrix. For simplicity, the elasticity of the matrix has been considered isotropic, which means that the elastic properties (i.e., Young modulus and Poisson’s ratio) are same in all directions. Although the matrix includes some fibrillar components such as elastin and protein cross bridges, their content is small and unlikely to significantly alter the assumption of isotropy. However, transport properties such as permeability and diffusivities have been shown to be anisotropic (Gu et al. 1999; Travascio and Gu 2011), which means that there are directions where the fluid and solutes can flow or move with less resistance.
The tensile properties of the annulus fibrosus have been characterized using uniaxial and biaxial tension tests (Jacobs et al. 2013; Nerurkar et al. 2010). In uniaxial tests, a strip of tissue is cut from the annulus fibrosus in a given orientation (circumferential, axial, radial, or along the fibers), and the force required to stretch the sample is recorded as a function of the applied strain. The Poisson’s ratio can be measured by recording the lateral contraction of the sample during the test. The Young modulus is calculated from the slope of the stress–strain response. A summary of these properties is presented in Table 2.2. The Young modulus is higher in the disc’s circumferential direction than the axial. This is expected since the fibers are oriented closer in the circumferential direction; therefore, fibers are not stretched during axial loading so that modulus is primarily due to the matrix.
Circumferential | Axial | Radial | ||||
|---|---|---|---|---|---|---|
ND | D | ND | D | ND | D | |
Inner anterior | 5.6–10.0 | 5.0 | 1.0 | – | – | – |
Outer anterior | 17.0–29.0 | 22.0–29.0 | 0.8 | – | 0.4–0.5 | 0.4 |
Inner posterior | 2.0–6.0 | 4.0 | – | – | 0.5 | – |
Outer posterior | 13.0–19.0 | 8.0 | – | – | – | – |
Biaxial loading is another tensile test used to quantify annulus fibrosus mechanics. It is thought that biaxial loading more closely resembles multiaxial physiological loading of the annulus fibrosus (Bass et al. 2004; Gregory and Callaghan 2011; Huyghe 2010; Jacobs et al. 2013; O’Connell et al. 2012). For this test, a rectangular thin sample is gripped on all four sides and loads are applied in two directions (Fig. 2.3). Two-dimensional deformations are optically recorded during the test. Unlike a uniaxial test, there is not a direct relationship between the slope of these curves and the elastic properties of the annulus fibrosus; the forces (or stress) in one direction are affected by the deformation applied to the other direction (O’Connell et al. 2012). Consequently, the data from biaxial tests are analyzed through the use of a model. The advantage of using biaxial experiments to characterize the mechanics of the fibers is that the values obtained through these types of tests can be used to predict the response of the annulus fibrosus in uniaxial tests and with other biaxial strain ratios (O’Connell et al. 2012).


Fig. 2.3
In a biaxial test of annulus fibrosus, a sample is loaded simultaneously in the axial and circumferential direction
Since the collagen fibers only contribute to the mechanics of the annulus fibrosus in tension, the elastic properties of the extrafibrillar matrix can be measured through confined compression tests (Cortes and Elliott 2012; Drost et al. 1995; Klisch and Lotz 2000; Perie et al. 2005). This test provides the aggregate modulus, measured as a function of strain. Similar to the nucleus pulposus, the mechanical behavior of the matrix depends on contributions from the osmotic pressure and the nonionic extrafibrillar matrix (Cortes and Elliott 2012). In this manner, the mechanical properties of this extrafibrillar matrix can be measured in tension and compression by applying osmotic swelling and confined compression simultaneously. The nonionic extrafibrillar matrix is nonlinear with a higher stiffness in compression (∼50 kPa) than in tension (∼10 kPa), and the contribution of the osmotic pressure in the support of the applied loads is high (∼70 % of total) when the EFM is in compression and low (∼25 %) when in tension.
Shear tests have been used to determine elastic and viscoelastic properties of the annulus fibrosus. Elastic shear properties have been measured by applying simple shear tests (Fujita et al. 2000; Hollingsworth and Wagner 2011; Iatridis et al. 1999; Jacobs et al. 2011). Since the fibers have a contribution during this test, the shear modulus is anisotropic with a higher modulus in the circumferential–axial plane where the fibers experience stretches (Table 2.3). On the other hand, torsion tests have been used to measure viscoelastic properties of the annulus fibrosus (Iatridis et al. 1999). The dynamic modulus increases with frequency. Both equilibrium and dynamic modulus decrease with shear strain amplitude. The highly viscoelastic nature of the annulus fibrosus is evidenced by the threefold increase of the dynamic modulus over the equilibrium modulus.
Table 2.3
Shear modulus (kPa) of human annulus fibrosus: effects of sample orientations and location and type of test
Type of test | Location | Orientation | ||
|---|---|---|---|---|
Circ-radial | Circ-axial | Radial-axial | ||
Simple shear – compressive preload | Anterior | 28.92 | 58.56 | 40.16 |
Simple shear – compressive preload | Posterolateral | 22.2 | 53.6 | 25.1 |
Simple shear – tensile preload | Anterior | – | 193.6 | – |
Torsion shear – equilibrium | Anterior | 20–100 | – | – |
Torsion shear – dynamic | Anterior | 100–280 | – | – |
Although separating the mechanics of the annulus fibrosus into fibers and matrix is very convenient and describes much of the mechanical behavior of annulus fibrosus, there are interactions between these components. Specifically, the stiffness of the matrix increases with the stretch of the fibers (Guo et al. 2012). To account for these effects, several fiber–matrix and fiber–fiber interactions have been formulated in terms of the strain perpendicular and along the fibers (Guerin and Elliott 2007; O’Connell et al. 2009, 2012; Wagner and Lotz 2004). These interactions have more accurately described the mechanical behavior of the annulus fibrosus. It has also been suggested that shear interactions are essential to obtain a good simultaneous prediction of uniaxial, biaxial, and shear experimental data (Hollingsworth and Wagner 2011; O’Connell et al. 2012).
While many aspects of the mechanical behavior of the annulus fibrosus have been well described, this is still an active area of research. Special attention needs be given to relations between interactions and composition of the annulus fibrosus and the contribution of these interactions to mechanics of the disc. Additionally, these interactions between components should be replicated in engineered tissues that are currently being investigated as therapeutic alternatives (Mauck et al. 2009; Nerurkar et al. 2010).
2.2.4 Cartilaginous Endplate
The biomechanics of the cartilaginous endplate has been far less studied than other disc tissues. The endplate is the interface between the nucleus pulposus and inner annulus fibrosus with the vertebral bodies (Fig. 2.1a). It covers most of the vertebral endplate except for a small ring in the periphery called the ring apophysis. The thickness of the cartilaginous endplate varies: it is thinnest in the center (∼0.2 mm) and thickest in the periphery (∼0.9 mm) (Moon et al. 2013). The composition of the cartilaginous endplate is similar to that of hyaline cartilage, which is characterized by a high proteoglycan and collagen II content. The water content of human endplate is 58 % of the wet weight, the s-GAG content is 17 % of the dry weight, and the total collagen content is 60–80 % of dry weight (Setton et al. 1993). The cartilaginous endplate plays an important role in the transport of nutrients and other metabolites into the nucleus pulposus and the inner portion of the annulus fibrosus.
The mechanics of the cartilaginous endplate has been measured using confined compression tests (Setton et al. 1993). The aggregate modulus of the baboon endplate is 0.44 MPa. The hydraulic permeability (14.3 × 10−14 m4/Ns) is considerably higher than values of 0.09 × 10−14 m4/Ns and 0.153 × 10−14 m4/Ns for the human annulus fibrosus and nucleus pulposus, respectively. The high permeability value suggests that its main function is to allow the transport of fluids, nutrients, and waste products to the cells in the nucleus pulposus and part of the annulus fibrosus.
2.3 Intervertebral Disc Mechanics
In the previous sections, the mechanics of individual disc tissues were described separately. However, these tissues interact with each other providing the disc with a special mechanical behavior. In a similar way, a disruption or a change in mechanical properties of one of these tissues causes an impairment of the mechanical function of the overall disc. In this section, disc mechanics are presented as the contribution of individual tissues during a given loading scenario. First, the residual stresses in the unloaded disc are briefly described. Then, the mechanics of the intervertebral disc are analyzed for three of the most important loads: axial compression, bending, and torsion.
2.3.1 Stress and Strain in the Unloaded Disc
Before analyzing the mechanics of the disc under different types of loading scenarios, it is important to understand the impact of internal stresses and strains on the unloaded disc. As described above, at the tissue level, the osmotic pressure is balanced by tensile or “residual” stresses. In a similar way, at the disc level, there are residual stresses and strains due to osmotic effects caused by tissue proteoglycans, are present even in the absence of applied loads. When external loads are applied to the disc, additional stress builds up above that of the residual stress. There are several mechanisms, at different scales, contributing to residual stress (Lanir 2009). At the micro-level, the interaction between proteoglycans, ions, water, and the collagen network produces an osmotic pressure that contributes to the total stress of the tissue. At the meso-level, residual stress arises from inhomogeneities within the tissues, e.g., the gradient of proteoglycan and collagen content from inner and outer annulus. Residual stress at meso-level has been recently measured in terms of the opening angle after a radial cut in bovine annulus fibrosus rings (Michalek et al. 2012). This effect is similar to that observed in aortic arteries, where differences in proteoglycan content between the media and the adventitia contribute to this component of the residual stress (Azeloglu et al. 2008; Chuong and Fung 1986). At the disc level, residual stress is also generated by the interaction between different tissues (nucleus pulposus, annulus fibrosus, endplates, and vertebral bodies). The high proteoglycan content of the nucleus pulposus results in a significant osmotic pressure. This pressure has been measured in vitro and in vivo using a needle pressure gauge (Nachemson 1981; Panjabi et al. 1988; Wilke et al. 1996, 1999). The radial expansion of the nucleus is constrained by the annulus fibrosus through tensile stresses in the circumferential direction (hoop stress) and compression stress in the radial direction. Similarly, the osmotic pressure in the nucleus tends to vertically separate the vertebral bodies, which are held in place by tensile stresses in the annulus fibrosus in the axial direction. All these contributions to the residual stress of the disc create a multidirectional and inhomogeneous initial state of stresses and strains that must be considered for the analysis of disc mechanics.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








