Chapter 17 Does Strain in the Patella Change After TKA? A Finite Element Investigation of Natural and Implanted Patellae

Clare K. Fitzpatrick, Mark A. Baldwin, Azhar A. Ali, Peter J. Laz, Paul J. Rullkoetter

DISCUSSION

Patellar fracture and anterior knee pain remain as significant complications following total knee replacement (TKR). In several TKR studies reported in the literature, the average incidence of anterior knee pain was 12%.¹² Recent long-term, large-cohort studies have reported patellar fracture rates of 0.68%, 1.14%, 3.8%, and 5.2% in TKR populations involving 12,424, 1494, 4583, and 8530 knees, respectively.^5,^14,^20,²³ Even at these relatively low incidence rates, the number of patients experiencing these complications is significant, especially considering the growing number of TKRs performed worldwide. A wide variety of patellar fracture types and locations have been reported.^5,^9,²³ Fracture type classification includes transverse, vertical, avulsion, and comminuted, with fracture location reported as 40% superior or midbody and 30% inferior pole by Goldberg and associates,⁹ and as 28% superior, 18% inferior, 23% comminuted, 13% vertical, 11% transverse midbody, and 6% medial or lateral margin by Ortiguera and Berry.²³

Treatment of patellar fracture varies considerably from case to case. A substantial proportion of patellar fractures are asymptomatic and are identified only radiographically upon routine follow-up. Others present with anterior knee pain, swelling, reduced range of motion, catching, locking or giving way of the joint, and/or difficulty with daily activities ^5,⁹ and may require bracing, open reduction, internal fixation, component revision, or partial or total patellectomy.⁷ Revision surgeries have been reported with poor outcomes, including high rates of complication (50%) and reoperation (42%).²³ Goldberg and colleagues⁹ described unsatisfactory outcomes in 13 of 18 (72%) knees that underwent revision for patellar fracture. Keating and coworkers¹⁴ reported a deep infection rate of 45% of patellar fractures treated operatively.

Given the number of occurrences and the high rate of complication with revision procedures, patellar fracture represents a significant concern affecting comfort and functionality for a substantial number of patients. If the patient subset at risk for patellar fracture or anterior knee pain can be identified preoperatively, alternative treatments (e.g., selection of a specific implant design, altered component placement, an unresurfaced patella) can be applied, and this may reduce the rate of complications. Meding and associates ²⁰ investigated patient and surgical factors associated with increased risk of patellar fracture, identifying a body mass index greater than 30, male gender, lateral reticular release, and a large patellar component size as risk factors. Dalury and Dennis⁶ reported postoperative patellar resection thickness and asymmetrical patellar resection as important contributing factors to patellar fracture.

Previous studies have measured strain in the patella, using strain as a measure of risk for patellar fracture and component loosening.^18,^30,³⁴ In these experimental cadaveric studies, anterior surface strain was measured using a uniaxial strain gauge in specimen sample sizes of between 8 and 20 knees. A strain gauge can provide a localized measure of bone strain but does not fully characterize the strain distribution throughout the volume of bone. For example, Lie and colleagues¹⁸ measured compressive anterior cortex strain in full extension and hypothesized that this would result in corresponding tensile strain on the posterior resected surface.

Recently, subject-specific finite element analyses have been used to determine bone strain distributions in the hip, femur, and tibia, and have been applied to assess fracture risk, evaluate fixation, and predict bone remodeling.* If accurate results are the goal, it is important to account for the varying material properties of bone as a function of density. Objectives of this study were (1) to develop subject-specific finite element (FE) models of the patellofemoral (PF) joint during deep flexion, including density-mapped material properties from computed tomography (CT) scan data; (2) to quantify differences in bone strain distribution under natural and implanted conditions; and (3) to assess the consistency of distributions across multiple specimens. An understanding of bone strain distributions under natural and implanted conditions can provide insight into important factors (geometry, bone density) and may allow preoperative identification of at-risk patients.

Materials and Methods

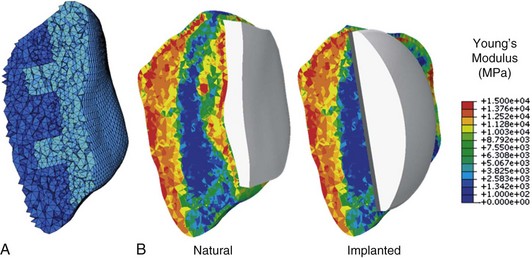
Specimen-specific finite element models for eight male subjects were developed from CT and magnetic resonance imaging (MRI) scans of cadaveric knees. Femoral, tibial, and patellar bone and cartilage were reconstructed from MRI data, while patellar bone geometry was extracted from CT data. Eight-noded hexahedral meshes of articular cartilage were semiautomatically generated from the segmented geometries using custom-scripted coordinate data extraction and mesh morphing techniques.² A convergence study was performed to determine an appropriate element size for the patellar bone mesh. Tetrahedral meshes with element edge length of 1.25 mm, 1 mm, and 0.8 mm were compared. Differences in average strain (per unit volume) between the coarsest and finest mesh were less than 0.03% in natural and implanted models. Perillo-Marcone and coworkers²⁵ reported an element size comparable with the slice thickness of CT images to be sufficient for mesh convergence; they recommended an element size of 1.4 mm for convergence of Young’s modulus, along with stress and risk results with a CT slice thickness of 1 mm. CT slice thickness for specimens in the current study varied from 0.5 mm to 1 mm. Based on slice thickness, computational efficiency, and minimal differences between 1 mm and finest mesh, an average element edge length of 1 mm was determined to appropriately represent the heterogeneity captured by CT data. Patellar bones were meshed using four-noded tetrahedral elements, such that natural and implanted patellae shared an element subset (Fig. 17-1A). The shared anterior element set ensured that muscle load could be applied through a common extensor mechanism in both models, eliminating potential differences in load application. Average numbers of elements in natural and implanted patellae were 140,000 and 85,000, respectively.

Figure 17-1 A, Tetrahedral mesh of patellar bone for natural (both light and dark elements) and implanted (dark elements only) models. B, Patellar bone with mapped material properties in natural and implanted models.

Two model representations were developed for each specimen: a natural model with bone and cartilage, and an implanted model with a size-matched domed patellar button, a femoral component, and a tibial insert. Articular cartilage (E = 12 MPa, ν = 0.45)²¹ and the patellar component (E = 572 MPa, ν = 0.45)¹¹ were modeled as fully deformable. In the natural model, patellar cartilage nodes were equivalenced with the posterior patellar bone to facilitate load transfer to the bone. In the implanted model, TKR components were positioned under the guidance of an orthopedic surgeon, and an intermediate cement layer (E = 3400 MPa, ν = 0.3) was modeled between the patellar bone and button. Nodes were equivalenced between the button and the cement, and between the cement and the resected patellar bone surface. For computational efficiency, femoral and tibial bones, in addition to femoral and tibial components, were modeled as rigid bodies using triangular surface elements.

Patellar strain is dependent not only on geometry and loading and contact mechanics, but also on material properties of the bone. To account for specimen-specific bone material properties, mapped material properties of the patellar bone were extracted from CT data using BoneMat (Biomed Town) (Fig. 17-1B).³³ Calibration of CT data to correlate Hounsfield units (HUs) with apparent density (ρ) was performed using a linear relationship taken from the literature.²⁴ Several studies have derived empirical relationships between bone density and mechanical properties.^22,²⁴ The power law for Young’s modulus, E = 1990ρ,^3.46 as proposed by Keller¹⁵ was applied in this analysis. The nonlinear nature of the density–elasticity relationship ensures that different properties will be obtained depending on whether Young’s modulus for the element is calculated before or after averaging over the element. In a comparative study with experimentally obtained data, Taddei and associates³³ reported that transforming HU values into Young’s modulus values prior to averaging over the element was found to improve strain prediction accuracy compared with prior algorithms, which averaged HU values and then transformed them to modulus values. Hence, this material mapping algorithm was adopted for the current study and was applied using BoneMat (version 3).

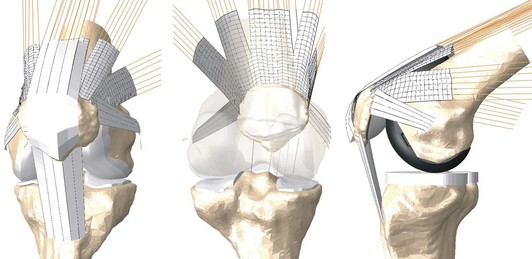
Each natural and implanted model was incorporated into an FE model of the isolated PF joint, which included two-dimensional (2D) fiber-reinforced membrane representations of the extensor mechanism and PF ligaments (Fig. 17-2).¹ An attachment site for each of the patellar ligament vasti, the rectus femoris, and the medial and lateral patellofemoral ligaments was defined on the surface of the patellar bone. Each node in the attachment site was rigidly beamed to its closest ligament fiber to physiologically transmit the ligament or muscle load to the patellar bone. A 1000 N ramped load was distributed among the heads of the quadriceps muscle as follows: vastus intermedius, 20%; vastus lateralis longus, 30%; vastus medialis longus, 15%; vasti lateralis obliquus, 10%; vasti medialis obliquus, 10%; and rectus femoris, 15%; these values are proportional to their physiologic cross-sectional areas as measured experimentally by Farahmand and colleagues.⁸ Prior to flexion, a 300 N load was applied to the quadriceps and was held constant to bring the PF articular surfaces into contact. The quadriceps load was then linearly ramped to 1000 N over a 120-degree simulated deep knee bend.