2 Biomechanics
Principles of WBV
The mechanism by which WBV works on the body is somewhat debatable. It has been shown that mechanical vibrations applied to the muscle belly or tendons are able to stimulate sensory receptors, mainly length-detecting muscle spindles (Hagbarth and Eklund 1966, Lance et al 1973). The primary endings of the muscle spindle (Ia afferent fibres), stimulated by the vibration of the muscle, facilitate the activation of the alpha-motoneurons causing reflex muscle contractions. This results in a tonic contraction of the muscle, referred to as the ‘tonic vibration reflex’, TVR, (Hagbarth and Eklund 1966, Lance et al 1973, Bishop 1974). Electromyogram data have revealed that this neuromuscular response, TVR, is mediated by monosynaptic and polysynaptic pathways (Bishop 1974) and results in increased motor unit activation (Burke and Shiller 1976). The effect of vibration is to elicit short fast changes in the length of the muscle-tendon complex. This input is detected as a ‘type of sensory stiffness’ through which reflex muscular activity will try to dampen vibratory waves (Figure 2.1).
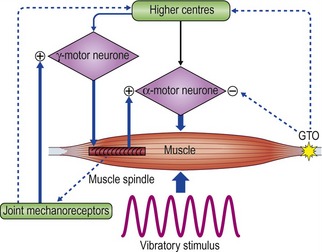
Figure 2.1 Schematic diagram illustrating stiffness regulation during vibration stimulation.
Reprinted from Cardinale M, Bosco C (2003) The use of vibration as an exercise intervention. Exercise and Sport Sciences Reviews 31(1):3–7, with permission.
The effects of vibration depend on the properties of the muscle itself. The response of the TVR is influenced by the frequency of vibration, whether the muscle is relaxed or contracted, the level of pre-contraction of the muscle, the position of the body (static) or association with movement (in terms of whether a muscle is shortening or lengthening) as well as the combined effect of all the muscles surrounding the joint (Fontana et al 2005, Ribot-Ciscar et al 2002, 2003). The vibration is not only perceived by neuromuscular spindles, but also by the skin, the joints and secondary nerve endings (Ribot-Ciscar et al 1989).
In contrast to single muscle stimulation, the use of WBV involves applications to the entire body. The stimulation, which comes distally from the platform, has a long way to go before it arrives at the sensors. Along the way, the stimulus of the vibration will change and it is quite difficult to assess the quantity of this change. Roll et al (1980) applied WBV on seated subjects and concluded that vibration acts on the extero- and proprioceptive receptors rather than on the vestibular organs. Johansson et al (1990, 1991) revealed that vibration would result in increases in muscle stiffness and joint stability due a relationship between activation of joint mechanoreceptors and stimulation of the gamma efferents. In a standing position, vibration has an effect not only on muscles and tendons, but also on the joint structures, which means that an additional potent sensory motor effect through the proprioceptive joint mechanoreceptors occurs. This may also be an important factor in explaining the manner in which vibration may enhance proprioception.
Although TVR is the most proposed mechanism as to the effect of WBV on muscles, there is not a clear consensus in the literature (Luo et al 2005). The connection between WBV and the TVR has not been fully discussed and demonstrated in the literature (Nordlund and Thorstensson 2007) and therefore further mechanisms have been proposed in this book encapsulating the idea of stimulating future research into this relatively new field of therapeutic WBV.
Simple harmonic motion (SHM)
Understanding SHM allows the clinician to appreciate how WBV imparts vibration to the body and how variation of body position affects the rate of loading (acceleration) at the various body parts. Spring feathering systems occur when a body is hung elastically. Similar to a stretched rubber band the muscles gain potential energy when they are lengthened, which can be converted to kinetic energy and hence movement when they reverse direction. The efficiency of energy transfer will determine the velocity and acceleration of the movement gained. SHM simply is ‘motion where the force acting on a body and thereby acceleration of the body is proportional to, and opposite in direction from the displacement from its equilibrium position’ (i.e. F = −kx ). WBV uses a range of frequencies up to 44 Hz to impart SHM to human tissue. The body reacts to this SHM in periodicities. Rubin et al (2003) used surgical pins in the L4 vertebrae to demonstrate that WBV frequencies in erect standing of less than 20 Hz imparted 100% transmissibility and therefore perfect resonance. Interestingly, at frequencies above 25 Hz this transmissibility decreased to approximately 80% at the hip and spine. Moreover, in relaxed stance transmissibility decreased to 60%, with 20° of knee flexion reducing this even further to 30%. This is clinically significant as it demonstrates that varying body position and joint angle will influence the site and rate of loading (acceleration) of the body part by WBV.
A general equation describing simple harmonic motion is
where x is the displacement, A is the amplitude of oscillation, f is the frequency, t is the elapsed time, and f is the phase of oscillation. If there is no displacement at time t = 0, the phase ϕ = π/2. A motion with frequency f has a period T = 1/f.
Motor control: length, stiffness and potential
Interestingly these oscillatory concepts of physics were used in the 1930s by a Russian mathematician, Nikolai Bernstein (1967), to describe a solution to the problems of motor learning for the control of the degrees of freedom offered by the human body in the context of the environment in which it is interacting (Kelso et al 1980, Kugler et al 1980, Turvey et al 1978a,b, 1981). Specifically, these latter authors used the Bernstein perspective to account for the speed at which the movement control calculation was happening. They suggested that the CNS uses feed-forward mechanisms based on prior movement experiences to set the tone of the spinal cord reflexes required for synergistic muscle activity. Investigations into WBV and the effect of superimposed voluntary contractions revealed increased excitability of the α-motorneuronal pool as exhibited by an increase in the Hoffman reflex (Nishihira et al 2002). During functional activities such as walking, inverse dynamics and three-dimensional analysis have shown that the hip, knee and ankle are predominantly driven at angles close to 0° and 180°, or stabilized at angles close to 90°. Moreover, the three joints are never fully driven and the hip and knee are mainly stabilized during the stance phase of gait (Dumas & Cheze 2008). Harmonic motion as described by Hooke’s law using a mass spring system analogy manages to account for the dynamics of a system of continuously altering control over ‘stability’ and its antithesis ‘mobility’. The total muscle tone around the joints is represented by the spring (Fig. 2.2).
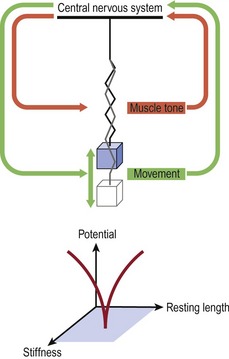
Figure 2.2 The Bernstein perspective of movement control using Hooke’s law and mass spring oscillation.
Reprinted and adapted from Kugler PN, Kelso JAS, Turvey MT (1980) On the concept of coordinated structures as dissipative structures. I: Theoretical lines. In: Stelmach GE, Requin J (eds) Tutorials in Motor Behavior 3–45, North Holland, Amsterdam.
Although WBV represents a stimulus of exceedingly small magnitude and short duration, in terms of the repetition needed for motor learning, a 25-Hz stimulus for 1 min equals 60 s × 25 Hz = 1500 cycles, which may represent 1500 steps while walking or running. Sufficient cross-sectional area and muscle tone ‘stiffness’ together with proportional muscle length generates the potential of the system. ‘Potential’ may be expressed clinically as improvements in jumping, counter movement jumping, and enhanced scores in the items of the Quality Metric outcomes measure SF-36.
Clinically, neurological conditions affecting muscle tone, disuse atrophy conditions affecting muscle mass (sarcopenia) and overuse training conditions affecting muscle length will all have an impact on motor control and the body’s ability to absorb and impart energy. WBV represents a novel training and rehabilitation form for the clinician as it can directly impart a stimulus to all three of these elements. Low-frequency vibration (<20 Hz) has been used to impart relaxation and change resting length (Haas et al 2006) or it can be used at higher frequencies (up to 44 Hz) to impart kinetic energy to the system, which increases the potential for movement through muscular recoil.
Because both velocity and acceleration can be derived from SHM equations they can be used to define the energy within a system. The amplitude of oscillation will depend upon the size (thickness, type of material and length) of the spring. Similarly, in the human body, muscle tone and body position will strongly influence the effect of energy capture and dissipation (Rubin et al 2003).
Stiffness
where E is Young’s modulus (modulus of elasticity), F is the force applied to the object, A0 is the original cross-sectional area through which the force is applied, ΔL is the amount by which the length of the object changes, and L0 is the original length of the object.
Resonance
where g is gravity’s constant (9.8 m/s2 for Earth), and L is length.
Resonance can be seen with WBV and is determined by muscle tone, by body positioning and through co-contraction (Rubin et al 2003, Feltham et al 2006). Indeed, Mahieu et al (2006) used WBV to improve strength and posture control in young competitive skiers.
Wakeling et al (2002) examined the resonance and damping properties of soft tissue while standing on a vibrating platform. Fourier transforms were used to calculate the amplitude of acceleration as a function of frequency a(f). The soft-tissue mass was considered a rigid mass for this analysis. For each given frequency f, the mean inertial power P required to oscillate the soft-tissue mass m was given by
Hereby they stated that the total inertial power 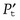 required for the oscillation in a particular direction is given by
required for the oscillation in a particular direction is given by
There was a time delay in response by the soft tissue of 150 ms, and this resulted in a decrease in the amplitude of the acceleration (Fig. 2.3).
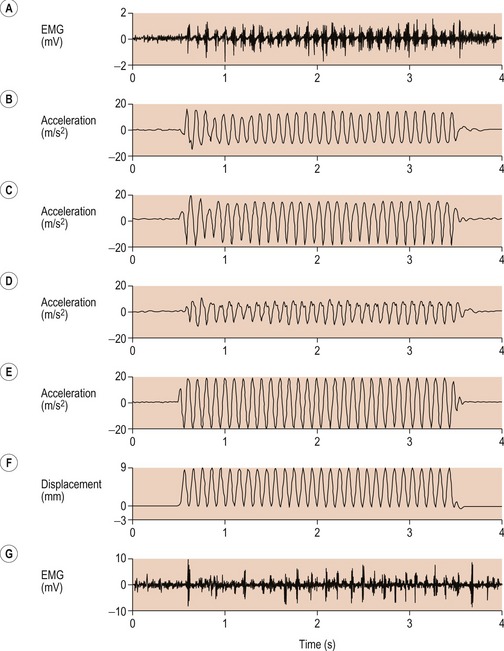
Figure 2.3 Electromyogram (EMG) trace from the medial gastrocnemius (A) and acceleration traces from the triceps surae (B–D) during one burst of continuous vibrations.
Reprinted from Wakeling JM, Nigg BM, Rozitis AI (2002) Muscle activity damps the soft tissue resonance that occurs in response to pulsed and continuous vibration. Journal of Applied Physiology 93:1093–1103, with permission from Penny Ripka.
Wakeling et al (2002) were able to demonstrate that elevated muscle activity and increased damping of vibration power occurred when the frequency input was close to natural frequency of each soft tissue.
Another investigation by Bazett-Jones et al (2008) examined the effects of WBV on acceleration by manipulating the variables of amplitude and frequency. Using an accelerometer they were able to show that 30 Hz at 2–4 mm = 2.16g, 40 Hz at 2–4 mm = 2.80g, 35 Hz at 4–6 mm = 4.87g and 50 Hz at 4–6 mm = 5.83g. They commented that less stiff people would require more neuromuscular activation to dampen the WBV stimulus.
Force exerted by stretched or compressed material
Young’s modulus of a material can be used to calculate the force it exerts under a specific strain
where F is the force exerted by the material when compressed or stretched by ΔL. From this formula Hooke’s law can be derived, which describes the stiffness of an ideal spring:
where
The relevance of compressed and tensile properties to humans becomes apparent when examining tensegrity modelling. Tensegrity views the musculoskeletal system as rigid bodies (bones and compressed fluid) situated within a mobile mass of muscle and soft tissue. As such the tension generated by muscles is countered by the wet and dry constituents of bone strength. Moreover, the pre-tension of muscles and other molecular cytoskeletal elements are thought to define the stability and movement capabilities of the human body. The understanding of tensegrity could fundamentally change the way we view the effect of WBV and will be discussed later in this chapter.
Elastic potential energy
The elastic potential energy stored is given by the integral of this expression with respect to L:
where Ue is the elastic potential energy. The elastic potential energy per unit volume is given by:
where
is the strain in the material. This formula can also be expressed as the integral of Hooke’s law:
Given mass M attached to a spring/pendulum with amplitude A with acceleration a:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


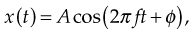
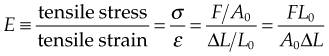
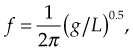
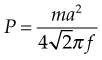
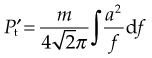
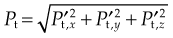
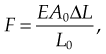
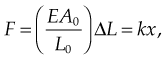
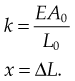
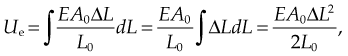
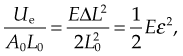
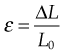
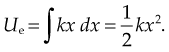
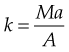
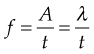
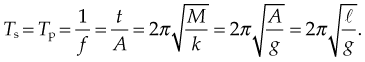
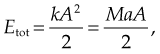
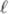 is the length of the pendulum, and Etot is the total energy.
is the length of the pendulum, and Etot is the total energy.





