Fig. 1
The four aligned channels of a patient data, left to right in-phase, opposed-phase, water and fat images (for visualization purpose, we only show the middle sagittal (mid-sagittal) slice of each channel)
2.2 Initialization
On the mid-sagittal slice, two landmarks are picked to indicate the centers of L1 and L5 vertebral bodies as shown in Fig. 2a.
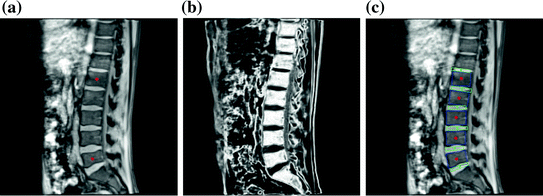

Fig. 2
Initialization and 2D lumbar spine column detection. a User initialization by picking two landmarks indicating the centers of L1 and L5 in the middle sagittal slice. b Probability assignment (displayed as grey values) of the bone tissue in the mid-sagittal slice for 2D lumbar spine column detection. c 2D lumbar spine column detection result using the graphical model based detection algorithm, blue and green rectangles representing the vertebral bodies and IVDs respectively (Color figure online)
2.3 Lumbar Spine Column Identification
Based on the initialization, we first carry out a 2D vertebral body and disc identification to localize vertebrae L1–L5 and the 5 target discs from the mid-sagittal slice. The geometrical information of the 2D identification is then used to guide a further 3D lumbar spine column modeling.
2.3.1 2D Vertebral Body and Disc Identification
Solutions for spine location and disc labeling include feature-based bottom-up methods, statistical model-based methods and graphical model-based solutions. For a detailed review of the existing methods, we refer to [14, 15]. In this paper, the 2D vertebral body and disc identification is achieved using a graphical model based strategy introduced in [14]. Compared with the graphical models in [5, 6], the advantage of the graphical model in [14] is that both the low level image observation model and the high level vertebra context potentials need not to be learned from training data. Instead they are capable of self-learning from the image data during the inference procedure. The basic idea is to model both the vertebral bodies and discs in the mid-sagittal slice as parameterized rectangles, where the parameters are used to describe the geometries of these rectangles including their centers, orientations and sizes. The graphical model based spine column identification can be understood as matching the parameterized models with the observed images while also considering the geometrical constraints between neighboring vertebral bodies and discs. The exploration of geometrical constraints between vertebral components helps to enhance the identification robustness.
1.
The graphical model: The graphical model used in this work to represent the lumbar spine column is given in Fig. 3. In this model each node V i represents a connected disc-vertebra-disc chain of the spine column, whose geometrical parameters are given by X i . On this graphical model we define
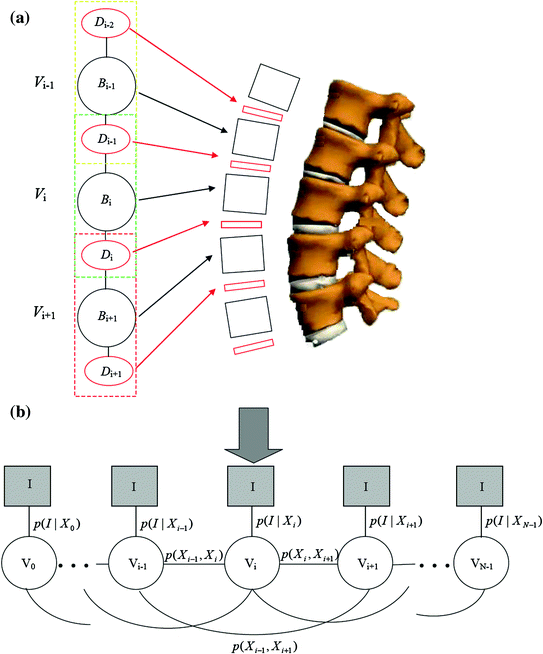

Fig. 3
Graphical model for the 2D lumbar spine column detection. a A node V i represents a disc-vertebra − disc (D i−1 − B i − D i ) chain of the lumbar spine and both the discs and vertebrae are modeled as parameterized rectangles. b The observation model p(I|X i ) of each node V i and potentials p(X i , X j ) between nodes V i , V j defined on the graphical model
The component observation model p(I|X i ) of a single component V i representing the probability that the configuration X i of the node V i match the observed images I.
The potentials p(X i , X j ) between neighboring components V i and V j encoding the geometrical constraints between components which are defined by the anatomical structure of the spine column.
The identification of the spine column from the mid-sagittal slice can then be formalized as to find the optimal configurations of {V i }, X = {X i } that maximize
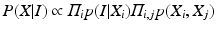
with
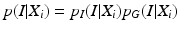
and
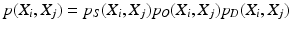
p I (I|X i ) and p G (I|X i ) stand for the probabilities that the observed image intensity and image gradient distributions match the geometrical parameters X i respectively. p S (X i , X j ), p O (X i , X j ) and p D (X i , X j ) are the geometrical constraints on the sizes, orientations and distances between neighboring components. All the observation models and constraints can be designed according to the observed data and prior anatomical knowledge of the spine structure. For detailed formulation of these terms, we refer to [14].
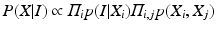
(1)
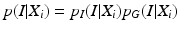
(2)
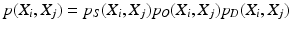
(3)
2.
Preprocessing of the 4 channel data: In order to achieve the model fitting simultaneously on the 4 data channels, we need a preprocessing to combine the information from different data channel. As shown in the introduction of the graphical model, in the component observation model p(I|X i ), both the image intensity and gradient information are used by p I (I|X i ) and p G (I|X i ) respectively. In order to combine the information of the 4 channels, we firstly observe that besides the positions of L1 and L5, the two user selected landmarks and the mid-sagittal slice also provide intensity distribution information of the bony tissue in the 4 channel volumes. For the intensity information, by fitting a Gaussian distribution N(μ i , σ i ), i = 1, 2, 3, 4 to a small neighbourhood of the initialization landmarks on each data channel, we can estimate the intensity distribution of the bone region of that data channel and accordingly assign to each pixel at position (l, k) with intensity value x i (l,k) of the mid-sagittal slice a value 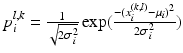 indicating the probability that the pixel belongs to the vertebral body. The combined bone assignment probability information of the 4 channels can then easily be obtained by an equally weighted averaging of the 4 channels as
indicating the probability that the pixel belongs to the vertebral body. The combined bone assignment probability information of the 4 channels can then easily be obtained by an equally weighted averaging of the 4 channels as 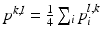 . Similarly we can also combine the gradient information of the 4 data channels by simply averaging the gradient amplitude of each channel. The combined intensity and gradient information are then used in the intensity and gradient local observation model components, p I (I|X i ) and p G (I|X i ), of the graphical model. Figure 2b shows an example of the bone tissue probability assignment on the mid-sagittal slice computed from the user supplied 2 landmarks (Figs. 2a and 4 channel volume data (see Fig. 1 for an example).
. Similarly we can also combine the gradient information of the 4 data channels by simply averaging the gradient amplitude of each channel. The combined intensity and gradient information are then used in the intensity and gradient local observation model components, p I (I|X i ) and p G (I|X i ), of the graphical model. Figure 2b shows an example of the bone tissue probability assignment on the mid-sagittal slice computed from the user supplied 2 landmarks (Figs. 2a and 4 channel volume data (see Fig. 1 for an example).
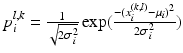 indicating the probability that the pixel belongs to the vertebral body. The combined bone assignment probability information of the 4 channels can then easily be obtained by an equally weighted averaging of the 4 channels as
indicating the probability that the pixel belongs to the vertebral body. The combined bone assignment probability information of the 4 channels can then easily be obtained by an equally weighted averaging of the 4 channels as 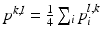 . Similarly we can also combine the gradient information of the 4 data channels by simply averaging the gradient amplitude of each channel. The combined intensity and gradient information are then used in the intensity and gradient local observation model components, p I (I|X i ) and p G (I|X i ), of the graphical model. Figure 2b shows an example of the bone tissue probability assignment on the mid-sagittal slice computed from the user supplied 2 landmarks (Figs. 2a and 4 channel volume data (see Fig. 1 for an example).
. Similarly we can also combine the gradient information of the 4 data channels by simply averaging the gradient amplitude of each channel. The combined intensity and gradient information are then used in the intensity and gradient local observation model components, p I (I|X i ) and p G (I|X i ), of the graphical model. Figure 2b shows an example of the bone tissue probability assignment on the mid-sagittal slice computed from the user supplied 2 landmarks (Figs. 2a and 4 channel volume data (see Fig. 1 for an example).
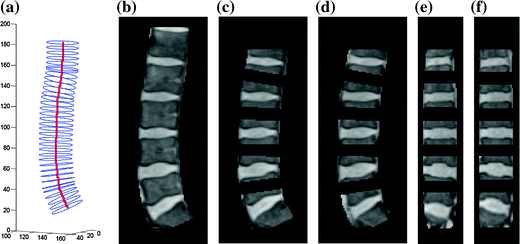
Fig. 4
3D lumbar spine column detection and modeling. a The 3D soft-tube model of the lumbar spine column; b segmented lumbar spine column image; c–d segmented disc candidate regions in sagittal slices; e–f segmented disc candidate regions in coronal slices. Although all tasks are conducted in 3D, here we show the results in 2D slices for visualization purpose
3.
Optimization: The optimization is achieved as an inference on the graphical model, which is essentially a particle based nonparametric belief propagation on the graphical model as described in Algorithm 1. The outputs are then the 2D geometrical parameters of the spine column which best fit the observed mid-sagittal slices of all the 4 data channels.
4.
Detection results: Fig. 2c gives the 2D lumbar column detection result. It can be observed that the centers, sizes and orientations of the vertebral bodies and IVDs are correctly identified.
Algorithm 1 Graphical model based inference for 2D lumbar spine column detection |
|---|
Input: Bone region assignment map (Fig. 2b) from mid-sagittal slices of the 4 data channel, landmarks from user initialization Output: 2D geometrical parameters of the lumbar vertebral bodies (L 1 − L 5) and discs between L 1 − S 1 Initialization: Roughly estimate the possible configuration regions of the positions, sizes and orientations of each vertebral body and disc according to the user initialization and prior anatomical information of the lumbar spine. Start: t = 0, draw N random samples configurations of {X i n (t), n = 1, …, N} of each model node V i from the estimated parameter space. while not converge do 1. Compute the belief of each particle X i n (t) by the local observation model as b i n (t) ∝ p(I|X i n (t)). 2. Run belief propagation till converge on the chain graphical model using the potentials 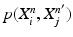 among nodes to update the belief of each particle X i n (t) to obtain updated believes among nodes to update the belief of each particle X i n (t) to obtain updated believes 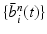 , which are the approximations of the marginal probabilities P(X i n |I) given in (1) obtained by the belief propagation. , which are the approximations of the marginal probabilities P(X i n |I) given in (1) obtained by the belief propagation.3. Re-sample the particles according to the updated believes 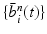 to obtain new samples to obtain new samples 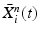 of each node. of each node.4. Update the configuration of each sample 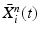 by a Gaussian random perturbation on the parameters to obtain new particles {X i n (t + 1)}. by a Gaussian random perturbation on the parameters to obtain new particles {X i n (t + 1)}.5. t = t + 1. |
end while For each node V i , the parameters of the particle with the highest belief are selected as the configuration of that node and therefore the geometrical parameters of the vertebral bodies and discs are estimated. |
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








