Methods for Studying Knee Contact Mechanics

In vitro experimental testing protocols incorporating knee simulators, with or without the use of cadavers, are widely used in evaluating kinematics, influence of soft tissues and wear, and longevity of nonimplanted and implanted knees.^29,³⁷ Knee simulators represent a critical step in the design process of new TKA. However, the standarized protocols used fail to simulate the actual operating conditions,³⁵ in which considerable intersubject variability exists both in terms of kinematics and kinetics, especially for TKA subjects.²⁷

Although the use of invasive in vivo experimental techniques, including the use of fracture fixation devices, bone pins, minimally invasive halo ring pin attachments, and roentgen stereophotogrammetric analysis (RSA), have been found to provide a high accuracy in kinematic measurements, the use of noninvasive in vivo methods have superseded them in popularity. Currently, the most popular methods used for in vivo motion analyses are skin markers and medical imaging. Because of the relative movement of the skin over underlying osseous structures,³ skin marker technology applying suitable correction measures, such as artifact assessment, point cluster technique, and optimization using minimization, is used extensively when high-speed multibody movement need to be tracked.¹ For slow-speed weight-bearing activities, the use of single-plane and biplanar fluoroscopy^12,^15,^23,²⁸ or open and closed magnetic resonance imaging (MRI) modalities,^11,^13,^14,¹⁹ coupled with two-dimensional to three-dimensional image registration techniques, have become the gold standard because of the low amount of error associated with the process.

In vivo force measurements using telemetric knee implants have been reported and have provided invaluable insights into the kinetics of the implanted knee.^8,^9,⁴⁰ However, the high costs involved in its development, telemetry still has not been used on a mass scale. Moreover, this technology is not feasible for studying normal knee joint forces. Therefore, computational modeling has always been a necessity for studying the contact forces occurring at the knee joint.²⁰ Because of the indeterminate nature of modeling the knee with more unknowns than equations, reduction methods and optimization methods have been used to obtain a solution.²⁷ In the optimization technique, the number of unknowns is greater than the number of equations that can be generated for the solution. Consequently, the process deals with the solution generated by the minimization of a suitably chosen objective function. However, there still lacks a consensus as to which objective function is physiologically most suitable. Possibly, with optimization, you will achieve a mathematically correct solution, but it may not be physiologically correct. The reduction technique, on the other hand, uses simplifying assumptions to reduce the complexity of the system. In this case the system is always kept determinate—that is, the number of unknowns is always made equal to the number of equations that can be generated to solve them. This method, therefore, generates a faster solution when compared with optimization, but only a certain number of unknown variables can be determined.

More recently, computed tomography (CT) and magnetic resonance imaging (MRI) base techniques have been used to study contact areas and pressures in the normal knee.^4,^25,³⁸ However, contact stress and strain variations are extensively studied using computational techniques. In this regard, the use of linear and nonlinear finite element analysis with biofidelic models segmented out of CT and MRI scans has been the most popular method for studying behavior in the normal knee, as well as in TKAs.^10,¹⁸ Because TKA components have regular geometry and the contact variation is elliptical in nature, faster contact algorithms using hertz contact, elastic foundation models, modified elastic foundation models, and explicit finite element analysis have also been used.^15,^17,³¹ Computational methods have also aimed to create virtual wear simulators using adaptive finite elements²¹ and an elastic foundation model coupled with a damage algorithm.¹⁶

Normal Knee Motion

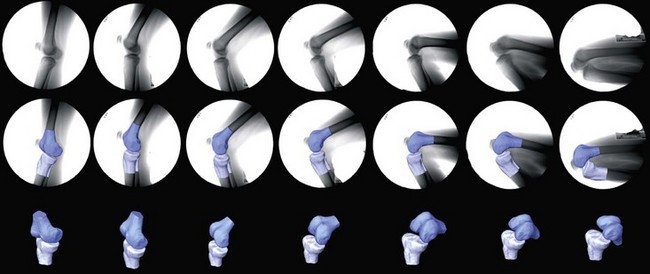
The kinematics of the normal knee is not a simple motion. The tibiofemoral articulation possesses six degrees of freedom,⁵ but three of these motions are more dominant in the knee—flexion-extension, internal-external rotation, and anterior-posterior translation. Abduction-adduction, medial-lateral, and superior-inferior translation might occur, but are minimal in magnitude compared with the other three motions. At full extension to very early stages of flexion (less than 10 degrees), the femur is internally rotated with respect to the tibia.^12,¹⁴ However, in weight-bearing deep knee bend and squatting exercises, with the increase in flexion, the femur starts to roll with slip on the tibia in the posterior direction (posterior femoral rollback) and the femur externally rotates with respect to the tibia^19,^24,²⁸ (Fig. 15-1). The external rotation of the femur with respect to the tibia with increasing flexion occurs as the lateral condyle moves more posteriorly than the medial condyle. The highest rates of axial rotation have been found to occur from full extension to 30 degrees of flexion.^11,³³ At this flexion range, the medial contact point translates posteriorly, mainly because of the change in the shape of the medial condyle.³² Above 30 degrees flexion, the knee enters the active functional arc and the axis of rotation crosses the centers of the almost circular posterior articular surfaces of both femoral condyles. In this phase, the medial contact point is relatively immobile or moves slightly in the anterior direction, allowing the lateral condyle to move relative to the medial condyle. Consequently, the longitudinal rotation of the femur occurs about an axis passing closer to the medial condyle. At very high ranges of flexion (greater than 140 degrees), thigh-shank contact sets in and influences the tibia to move anteriorly with respect to the femur. This causes both femoral condyles to move considerably posterior with respect to the tibia, and the lateral femoral condyle can reach the posterior edge of the tibial plateau.^38,³⁹

Figure 15-1 Sequence of fluoroscopic images (top) with CT-generated computer-aided design (CAD) models registered on them (middle) from full extension to maximum knee flexion. With the increase in flexion, the femoral condyles move posteriorly with respect to the tibia (bottom), coupled with an external axial rotation. At the onset of thigh-calf contact, both femoral condyles lie near the posterior edge of the tibial plateau.

Axial rotation of the femur with respect to the tibia is a critical factor in patellofemoral mechanics, allowing the patella to track along the anatomic trochlear grove of the femur.²⁶ In the normal knee, the patella always maintains contact with the femur.^22,³⁸ From full extension to 90 degrees of flexion, there is a single region of contact between the femur and patella. However, at flexion angles greater than 90 degrees, the contact areas divide into two separate regions with medial tilting of the patella and contacts with the odd facet at approximately 135 degrees of flexion. The most dominant motion in the patella is its flexion in the sagittal plane, which increases with the flexion of the femorotibial joint. This causes the patellofemoral contact locations to travel superiorly with respect to the patella.^13,³⁴

Normal Knee Forces

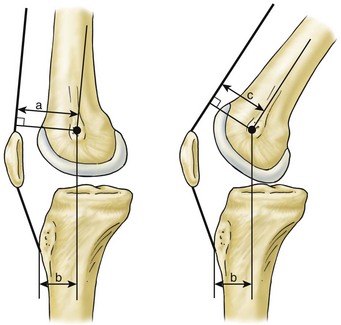
During a weight-bearing deep knee bend, normal knee flexion is mainly driven by the moment generated by the quadriceps muscles. The variation of the quadriceps forces are characterized by three distinct regions: (1) 0 to 90 degrees of flexion, in which the forces generally increases; (2) 90 to 120 degrees of flexion, in which the forces reach a peak; and (3) beyond 120 degrees, when the forces starts to decrease.³⁴ Because the femorotibial and patellofemoral contact forces are highly correlated with the force in the quadriceps, a similar variation in the pattern can be determined with respect to knee flexion. The moments generated by the quadriceps muscles is a function of the moment arm (perpendicular distance from the rotational center of the femoral condyles to the line of action of forces), cross multiplied by the force generated in the muscle.⁶ So, for the same total moment, an increase in the moment arm is reflected by a decrease in the force, and vice versa. The moment arm of the quadriceps muscle depends on the location of the femoral condyles and the angle of the quadriceps with respect to the tibia. As flexion increases, there is a decrease in the angle of the quadriceps with respect to the tibial plateau, causing the moment arm to decrease (Fig. 15-2). However, with increasing flexion, the femorotibial condyles also move posteriorly, tending to increase the moment arm (Fig. 15-3). Thus, the two effects can offset each other, causing the force to increase from 0 to 90 degrees. In the flexion range of 90 to 120 degrees, the quadriceps muscle wraps around the femur and therefore its angle, with respect to the tibial plateau, remains relatively constant. As a result, the moment arm is always increased because of the posterior movement of the femoral condyles causing the forces in the quadriceps and the femorotibial contact forces to decrease (Fig. 15-3). At very high flexion angles, the onset of thigh-calf contact reduces knee contact forces considerably.³⁹