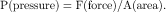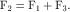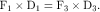Basic biomechanical principles

Statics

In this equation, the distance D (known as the lever arm) is defined as the perpendicular distance from the joint center to the line of action of the force (Fig. 22-1). Therefore, an orthosis that applies oblique, rather than perpendicular, forces will be less effective in generating the required moment because the lever arm will be smaller.

Fig. 22-1 Force (F) acting at distance (D₁) applies a moment (M₁). If the same force F acts obliquely, the lever arm is reduced (D₂), applying a smaller moment (M₂).

The creation of moments is the critical function of most lower limb orthoses. Increasing the lever arm is a clinically useful strategy because it enables the required moment to be generated while reducing the size of the applied force. Reducing the force reduces the pressure to which the tissue is subjected, with consequent benefits in terms of comfort and tissue viability. Pressure can also be reduced by increasing the area over which the force is applied. Increasing both the lever arm and the area over which force is applied maximizes function and comfort. In practice, of course, the lever arm is limited by the length of the anatomical segments involved or by other anatomical considerations such as tissue intolerance to pressure.

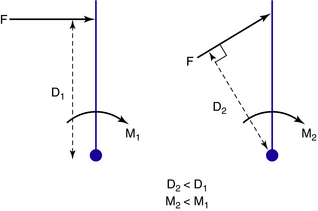
Equilibrium

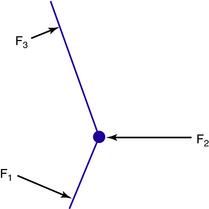
In order to work successfully, an orthosis must apply a system of forces that have been set up to balance each other, creating a state of equilibrium. This equilibrium relates not only to the forces but also to the moments created by these forces. To control angular motion at a joint, the minimum number of forces required is three, the so-called three-point force system (Fig. 22-2). Two of the forces in this system must be applied on the “concave” side of the joint, and these two forces must be balanced by the third force on the opposite side, which should be located as close as possible to the center of joint rotation. A state of equilibrium is illustrated in Fig. 22-3. Mathematically this state is expressed as follows:

Fig. 22-2 A minimum of three forces is required for control of angular motion at a joint.

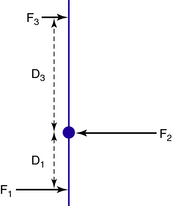
Fig. 22-3 The three-point force system is set up to be in equilibrium so that forces and moments balance.

Changing the magnitude of any one force in the system inevitably influences the magnitude of at least one of the others. If F₁ is increased, F₂ must also increase unless F₃ is decreased. However, the moments must also balance as expressed by the following equation:

If F₁ increases, then F₃ also must increase. Clinically, therefore, it is important to recognize that it is impossible to alter one force in a three-point force system without inevitably influencing the other two forces in the system.

In Figure 22-3 the three forces in the system are parallel to each other; however, this is not always the case. For example, the forces in the system that control ankle plantarflexion clearly are not parallel to each other, but they act in the same plane and still are in equilibrium (Fig. 22-4). This mechanical principle is known as a triangle of forces. From a practical point of view, in order to balance the other two forces and to “complete the triangle,” the force F₂ applied on the dorsum of the foot cannot act in a horizontal direction but must act diagonally downward. To be effective, any ankle strap should be attached in the direction in which this force is required to act.

Fig. 22-4 The three-point force system applied by an AFO to control ankle plantar flexion.

Shared overlapping force systems

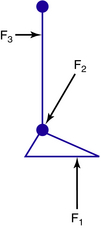
Because three is the minimum number of forces required to control rotation at a joint, one might reasonably assume that control of two joints requires forces to be applied at six places. However, if the two joints are adjacent to each other, some of these forces may be “shared.” This is seen when flexion at the knee and hip must be controlled simultaneously, for example, when using a standing frame, where two superimposed three-point force systems exist (Fig. 22-5). Forces F₁, F₂, and F₃ control knee flexion, while forces F₂, F₃, and F₄ control hip flexion. Thus, while each joint is indeed subject to a three-point force system, only four forces, strategically located, are sufficient to control adjacent joints.

Fig. 22-5 Forces can be “shared” when controlling adjacent joints.

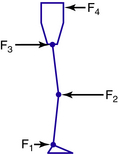
In the above example, the force systems act in the same plane, but this is not always the case. For example, in the valgus foot, the systems that control hindfoot eversion (coronal plane) and forefoot abduction (external rotation in the transverse plane) share a common force (F₃) at the lateral calcaneus (Fig. 22-6).

Fig. 22-6 Forces F₁, F₂, and F₃ control forefoot abduction; forces F₃, F₄, and F₅ control hindfoot eversion. Force F₃ is shared by both force systems.

Dynamics

The descriptions of static biomechanics are relevant to almost all situations involving orthoses. However, the treatment of locomotor disorders also necessitates consideration of the dynamic aspects of gait, including the accelerations and decelerations of the limb segments, particularly at specific instances of the gait cycle (Fig. 22-7).

Fig. 22-7 During normal locomotion, the shank and thigh segments flow through patterns of motion, with the shank reclined at initial contact flowing to inclined in late stance. Note that in midstance the forward motion of the shank slows down, indicated by the cluster of lines.

One example is the inertial effect associated with accelerating and decelerating the mass of the lower limb segments when initiating and terminating swing. Here the distal masses of the orthosis and shoe become significant. The larger the mass to be accelerated or decelerated (or the higher the required acceleration and deceleration, as seen in faster walking), the greater the muscle forces required. From a practical point of view, in most circumstances it is beneficial to minimize the mass of distally applied orthoses or footwear, in order to reduce the demand on the neuromuscular system.

Another clinically significant example occurs in midstance in normal gait when deceleration of the forward movement of the shank (lower leg) is coupled with acceleration of forward movement of the thigh. The influence of orthosis and footwear design on these movements are considered later.

Kinematics and kinetics

As well as controlling deformity, orthoses are often used to influence either motion of an individual joint or patterns of locomotion. The branch of mechanics that studies motion is known as kinematics. The branch of mechanics concerned with the effects of forces on motion is called kinetics. Consideration of both of these branches is relevant to understanding the biomechanical aspects of orthotic management of the lower limb.

Ground reaction force and moments

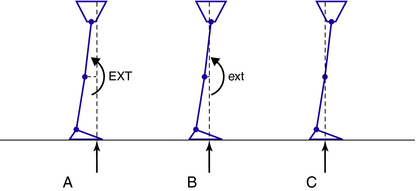
Due to gravity, the weight of the body acts vertically downward on the ground. In accordance with Newton’s third law, an equal and opposite force must act upward from the ground on the foot. This is known as the ground reaction force (GRF). Obviously there is no GRF during swing phase. The GRF has a point of application on the foot, or magnitude, and a direction, or line of action (Fig. 22-7). In static situations these all remain constant, with the magnitude equal to body weight. However, in dynamic situations such as locomotion (as will be seen later) they typically vary in a repetitive fashion. When the line of action of the GRF lies at a distance from the center of rotation of a joint, it creates an “external moment.” As we know, the greater the perpendicular distance of the line of action of the GRF to the joint center (the “lever arm”), the greater the external moment will be. If the GRF is aligned close to the joint center, the external moment is smaller. If the GRF passes through the joint center, then no external moment is generated.

The presence of an external moment tends to cause motion at a joint and usually (but, as we shall see, not always) requires the generation of an opposing internal muscle moment to create equilibrium or to control this motion. The greater the external moment, the greater the required internal moment likely will be. In static situations, the internal and external moments will be equal and opposite and therefore in equilibrium. However, in dynamic situations, such as locomotion, it may be necessary for the moments generated by the muscles to be slightly greater or less than the external moments in order to control angular motion at the joints.

During a gait cycle the GRF alignment may pass from one side of the joint center to the other, “switching” moments from, for example, flexion to extension (Fig. 22-8). This implies transfer in neuromuscular demand. For example, the switch from an external plantarflexion moment to an external dorsiflexion moment at the ankle during midstance requires a switch from dorsiflexor activity to plantarflexor activity.

Fig. 22-8 A, Ground reaction force (GRF) and external moments. GRF line of action in front of knee with large lever arm resulting in large external knee extension moment. B, GRF line of action closer to knee with smaller lever arm resulting in smaller external knee extension moment. C, GRF line of action passes through knee resulting in no external knee moment

However, the external moment sometimes creates a desirable effect at a joint, reducing or even removing the need for muscle activity. For example, a paraplegic patient fitted with knee–ankle–foot orthoses (AFOs) can achieve hip stability in standing by contriving to align the GRF posterior to the hip joints. At the end of joint range, the internal flexion moment required to balance the external extension moment may be generated (passively) by structures such as the ligaments or joint capsule. A dynamic example can be seen in the late stance phase of gait, when posterior alignment of the GRF to the hip extends and stabilizes the joint without the need for hip extensor activity (Fig. 22-8). This mechanism contributes to the energy efficiency of gait.

The exact magnitude of the external and internal moments (which are mutually dependent) generated at the joints is influenced by the accelerations and inertial effects of the individual limb segments.³⁹ For simplicity, the following discussion of gait ignores these influences. In clinical practice, consideration of the external moments resulting from GRF alignment and their modification by various forms of clinical intervention described later in this chapter can be a successful strategy.^3,^17,^27,^34,³⁵

Application of biomechanical principles to normal and pathological gait

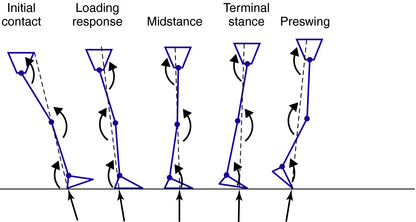
An appreciation of the biomechanical features of normal gait is an essential prerequisite to orthotic management of the lower limb. This chapter focuses on some important observations about normal gait biomechanics, which determine optimal prescription and design of lower limb orthoses. The normal gait of children and adults has been excellently described in depth.^10,^13,^18,^32,³⁸ The reader must be clear about the names of each of the phases and subdivisions of the gait cycle and the movements and forces that occur in each of these subdivisions in order to fully understand the concepts that will be discussed.³²

Normal gait has been defined as a highly controlled, coordinated, repetitive series of limb movements whose function is to advance the body safely from place to place with a minimum expenditure of energy.¹¹ Five attributes of normal walking have been described: foot clearance in swing, adequate step length, prepositioning of the foot at initial contact, stability in stance, and conservation of energy.¹¹ If we are to replicate these attributes with orthoses, we must understand how they are achieved in normal gait and the extent to which they are interrelated. For example, joint stability is fundamental to stance phase, but it also is a prerequisite for achieving adequate step length in the contralateral leg, which in turn facilitates prepositioning of the swing foot at initial contact.

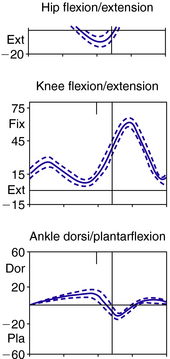
Most texts on normal gait and modern gait analysis focus on the kinematics of the joints, measured as angles between two adjacent segments. Typical graphs for hip, knee, ankle, and foot kinematics then can be produced (Fig. 22-9). However, understanding and giving equal consideration to the kinematics of the segments of the body is key to achieving optimal design of lower limb orthoses (Fig. 22-10). Movement of the segments can be measured relative to the vertical or the horizontal.^1,^13,³⁹ Measurement of the segment relative to the vertical can be expressed as degrees of incline (leaning forward from the vertical) or recline (leaning backward from the vertical).