Fig. 3.1
Bilateral standing X-ray of a 48-year-old male patient. After the history and physical exam findings, stress fracture of the medial tibial plateau was diagnosed
Although precise pathology is unknown, stress fracture refers to an overuse injury resulting in structural damage to the bone from repetitive weight bearing or increasing stressful muscular activity. Normal physiological loading provokes a range of deformation reactions in bone. The bone exhibits an intrinsic ability to adapt to alterations in chronic loading to withstand future loads of the same nature, a phenomenon referred to as Wolff’s law. The bone normally responds to strain by increasing the rate of remodeling. In this process, the lamellar bone is resorbed by osteoclasts, creating resorption cavities, which are subsequently replaced with denser bone by osteoblasts. Because there is a lag between increased activity of the osteoclasts and osteoblasts, the bone is weakened during this time. With cyclic loading, remodeling is given insufficient time to repair damage and additional loading cycles enabling damage to accumulate. Therefore, the bone fails to adapt adequately to the repetitive mechanical load experienced during physical activity [20]. In such cases, cessation of the load provides sufficient time period to remodeling phase.
Biomechanical factors may predispose to stress fractures by creating areas of stress concentration in the bone or promoting muscle fatigue. High arches, pes planus, leg length inequality, and medial deviation of the knee mechanical axes may predispose to various lower extremity stress fractures [21].
Stress fractures should be differentiated from insufficiency fractures which are bone injury in weakened bone (osteoporotic bone) from normal activity [22].
Introduction
Human musculoskeletal system works on principles based on a complicated cascade of movement and loads generated by gravity. The human body resists against applied loads and moves accordingly. The main components of the musculoskeletal system are bones, cartilages, tendons, and ligaments. Before proceeding with the biomechanical characteristics of these tissues, it may be appropriate to explain the term “load.”
Loads Generated on Musculoskeletal Tissues
Gravity is the most fundamental and consistent force on musculoskeletal tissues. Human movement is performed primarily against gravity. Resistance to gravity generated by skeletal muscles establishes the basis of the internal forces. Trauma however is associated with external forces affecting the skeletal system. Basically, the loads having an influence on the skeletal system and particularly on the bones are listed below (Fig. 3.2).
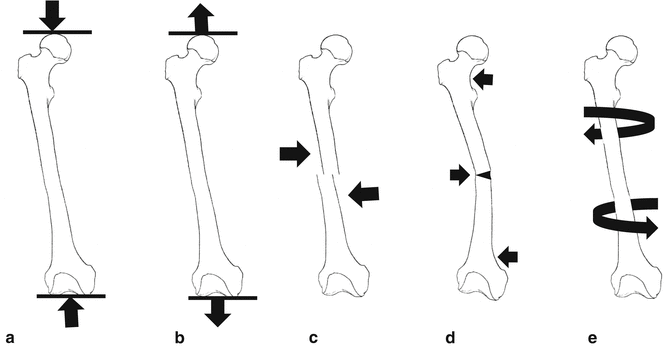

Fig. 3.2
Schematic drawing of loads on femur. (a) Compression, (b) distraction, (c) shear, (d) bending, (e) torsion
Load Types
Compressive Load
Forces inducing a compression leading to volume reduction by affecting the edges of an object. As will be discussed later, these forces have significance with regard to bone formation. However, a compressive load exceeding the compressive strength of the bones results in fractures. The most effective resistance to compressive load is manifested by the trabecular bone. Therefore, the loss of trabecular bone mass seen in osteoporosis is the leading reason behind spine and hip fractures.
Tensile Load
Forces aiming to stretch the length of a bone in the applied direction. As a result of the stretching effect, the width will decrease. Generally, this force is applied by the muscles of the body and transmitted by tendons to the bones. Primary resistance against the tensile forces is generated by the collagen fibers. Therefore, collagen fibers exhibit a longitudinal orientation at the bone-tendon attachment. Tensile force is the principal cause of the presence of apophysis. These growth centers located at the points of attachment between tendons and bones undergo ossification with age and remain as tubercles on the bones. In this regard, the tibial tubercle, to which patellar tendon is attached, is a good example. When the bone fails to exert adequate resistance to the tensile load transferred via tendon, avulsion fracture occurs. These fractures are often encountered in children. In some cases, injuries are observed in the apophysis prior to fracture. Such injuries are commonly observed in children making sports involving jumping. Apophysitis is seen at the tibial tubercle in Osgood-Schlatter disease and at the base of the fifth metatarsal bone in Iselin disease. The basic mechanism of injury in distention and sprain cases is also associated with tensile strength.
Shear Load
Shear stress arises from the force vector component parallel to the cross-section (Fig. 3.3). The main components of shear strength are compressive and tensile loads. The resistance potential of bone to shear forces is considerably low. Distal femoral and proximal tibial fractures occur because of shear strain associated with varus and valgus during knee hyperextension.
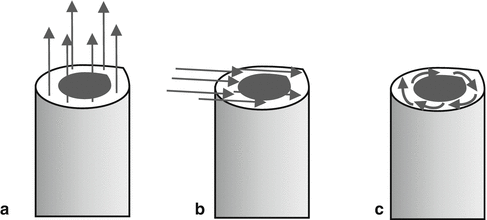

Fig. 3.3
Force vectors of loads. (a) Distraction, (b) shear, (c) torsion
Bending Load
Bending is a combination of compression and tension: tensile stresses and strains on one side of the neutral axis and compressive stresses and strains on the other side. Because the bone is asymmetrical, the compressive and tensile stresses may not be equal. Bending strength may occur with a three- or four-point load. The application of strength at three points usually involves strengths applied perpendicularly to the bone at the ends of the bone, with a strength applied in the opposite direction in the middle of the bone. Fracture begins on the tension side in adult bone as bone is weaker in tension than compression (Fig. 3.2d). A bending load is applied at four points with the application of two equal and opposite pairs of strength in each end of the bone [1]. In the case of four-point bending, the bone will break at the weakest point. An axial force applied on a nonunion of femoral fracture leads to the fracture to sustain a four-point bending load.
Torsion Strength
The shear stress induced by the rotational forces (Fig. 3.2e). As the distance of the point receiving the rotational forces increases, the torsion strength of the injury site rises as well. Such injuries are observed particularly in spiral oblique fractures [2] (Table 3.1). Nonetheless, torsional loads also play a role in intervertebral disk injuries.
Table 3.1
Estimated long bone fractures by applied loads
Fracture pattern | Mechanism of injury | Location of soft tissue hinge | Energy |
|---|---|---|---|
Transverse | Bending | Concavity | Low |
Spiral | Torsion | Vertical segment | Low |
Oblique-transverse | Compression-bending | Concavity or side of butterfly | Moderate |
Oblique | Compression -bending | Concavity (often destroyed) | Moderate |
Comminuted | Torsion variable | Destroyed | High |
Metaphyseal compression | Compression | Variable | Variable |
Action Forms of Loads
Three components of loading bear importance in understanding the subsequent injury: magnitude of load, duration of loading, and number of repeats. The magnitude of the applied load shows positive correlation with the magnitude of the response and the severity of the injury. This has a direct relationship with the first law of thermodynamics: “Energy cannot be created or destroyed, but it can change in form or be absorbed.” The resultant damage depends on the magnitude of the absorbed energy. At this point, it would be helpful to remember the third law of movement by Newton in predicting the injury to be induced: “When one object exerts a force on a second object, the second object simultaneously exerts a force equal in magnitude and opposite in direction on the first object.” If the object sustaining the load exerts a responsive force lower than that of the load, the exceeding portion of the load is absorbed by the object leading to its deformation. The body cannot respond adequately to the high energy released in traffic accidents; therefore, the exceeding energy is absorbed by the body and the resultant hardness leads to various damages in various tissues.
Duration of loading is also a factor in the resultant damage. In every speed of load placement, the bone can bear higher loads before fail. The bone that receives load slowly breaks with a load that is approximately half of that it could support if the load is more quickly applied. As we will see in the following pages, the duration of loading on biologic tissues plays a critical role in the severity of the damage as well as in the treatment.
Repeated loading induces a deformation depending on the magnitude and frequency of the loading. When applied with a repeated pattern, even the lowest loads can induce injuries on biological tissues. Stress fracture can be given as an example of such injuries [3].
Reading to Stress-Strain Curve
The main characteristic of tissues in the skeletal system is to manifest resistance to the applied forces. As happens in each object, the absorption of the applied force results in deformation in the biological tissues. The attributes of deformation shown by the material under load are evaluated with stress-strain curve. This evaluation gives us information about the stiffness and strength of the object. The area below the curve up to the failure of the biological tissue represents the toughness of the object which is one way to assess strength of the object, indicating the energy absorbed before the failure. Stiffness is about the inclination of the curve at elastic deformation stage which is expressed by Young’s modulus (stress/strain). As Young’s modulus value increases, the curve becomes steeper and the object becomes stiffer (Fig. 3.4). Depending on the variety of the terms of stiffness and strength, some objects may be described as stiff and strong (steel, iron), while some are described as stiff and weak (glass, copper). Fiberglass and silk are defined as flexible and strong, while spider web and lead are defined as flexible and weak materials. The bone is a flexible and weak material as well (Fig. 3.5).
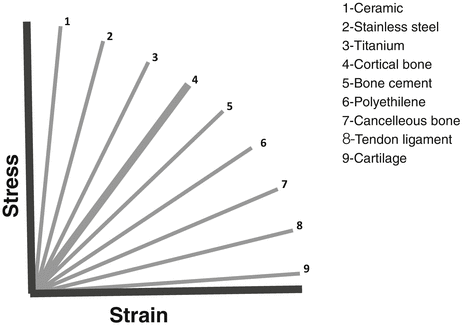
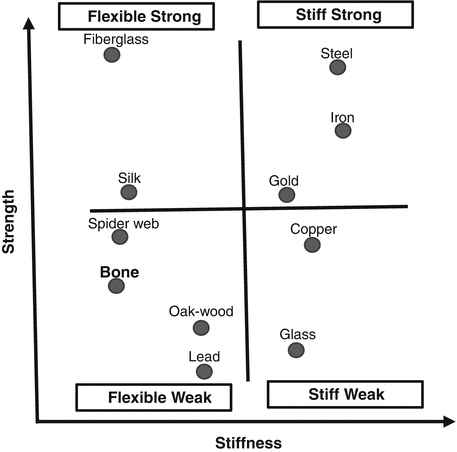





Fig. 3.4
Young’s modulus of the various materials, steepness of elastic deformation address to hardness (relative values of Young’s modulus)

Fig. 3.5
Definitions of some materials in terms of stiffness and strength
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








