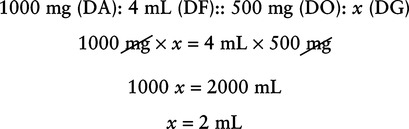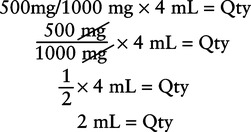Chapter 5 Upon successful completion of this chapter, the student will be able to: • Identify the weight and volume measures of the metric system. • Calculate the basic dosages related to the administration of IV medications, including percentages of solvents in standard IV fluids. • Interpret the meaning of abbreviated labels for common IV fluids. • Calculate drip rates of IV fluids. • Calculate flow rates of IV fluids. • Calculate infusion times of IV fluids. • Identify factors that might influence the flow rate of IV fluids. 1 gram = 1 g or to move to milligrams 1 g = 1000 mg Likewise, 1 milligram = 1 mg or to move to micrograms, 1 mg = 1000 mcg. To convert from 1 liter to milliliters, the same movement to the left is necessary or The metric system is shown in decimals because it is based on units of 10 (Table 5-1). To prevent medication errors when using the decimal system, always be sure that if a medication dose is a number less than one designation, a “0” should always precede that decimal point to prevent miscalculation of the dose to be given. Never allow a decimal point to be the first unit in a dosage indication (i.e., .025 mg should be shown as 0.025 mg or 25 mcg). Table 5-1 Metric Weight Volume 1 kg = 1000 g 1 g = 1000 mg 1 L = 1000 mL (cc) 1 mg = 1000 mcg 1 mcg = 0.001 mg 1 mg = 0.001 g 1 mL = 0.001 L The way to calculate the weight of solutes is by using ratio/proportion:
Review of Dosage Calculations
CALCULATING DOSAGE USING THE METRIC SYSTEM
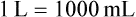
CALCULATING SOLUTE WEIGHTS DURING INFUSION
Known
Unknown
25 g dextrose (5 g/100 mL): 500 mL::x g: 300 mL
500 x = 7500 g
x = 15 g dextrose

Known
Unknown
4.5 g NaCl (0.9 g × 500 mL): 500 mL::x g: 300 mL
500 x g = 1350
x = 2.7 g ![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


Review of Dosage Calculations