) is not the highest power that a human can develop. Powers higher than the 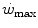 can be attained relying only on anaerobic metabolism as an energy source. In this case, the general equation of the energetics of muscular exercise takes the following form:
can be attained relying only on anaerobic metabolism as an energy source. In this case, the general equation of the energetics of muscular exercise takes the following form:
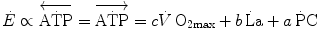
(6.1)
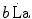 and
and 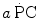 indicate the amount of ATP that is generated from anaerobic lactic metabolism and anaerobic alactic metabolism, respectively. These are analysed separately in this chapter. Of both, the power and capacity are quantified. From a more general perspective, the aim of this chapter was indeed to discuss the energetics of explosive supramaximal exercise.
indicate the amount of ATP that is generated from anaerobic lactic metabolism and anaerobic alactic metabolism, respectively. These are analysed separately in this chapter. Of both, the power and capacity are quantified. From a more general perspective, the aim of this chapter was indeed to discuss the energetics of explosive supramaximal exercise.I will treat anaerobic lactic metabolism first, of which some hints have already been given in previous chapters, especially as far as the genesis of early lactate accumulation during exercise transients is concerned. Several aspects of anaerobic alactic metabolism were also treated previously, as long as this is the main contributor to the obligatory component of the oxygen deficit. Anaerobic lactic metabolism as an energy source is, however, still a controversial issue on quantitative grounds, because several authors denied the possibility of performing a correct estimate of the metabolic energy corresponding to a mole of lactate accumulation in blood. As a consequence, the study of the energetics of anaerobic supramaximal exercise underwent decay in recent years, so that our current knowledge still relies mostly on the classical results obtained by the School of Margaria between the sixties and the eighties of last century. A preliminary discussion of the principles on which the energetic meaning of blood lactate accumulation is based is therefore necessary.
The Meaning of Blood Lactate in Supramaximal Exercise
Let us take as an axiom the concept that maximal oxygen consumption represents the uppermost limit of aerobic metabolism. As a necessary consequence, the metabolic power above 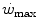 can derive only from anaerobic energy sources. Apart from the contraction of the obligatory component of the oxygen deficit, which occurs also in the early stages of a supramaximal exercise, reliance is mostly made on anaerobic lactic metabolism. On this basis, on the assumption that the overall metabolic power is directly proportional to the applied mechanical power also during supramaximal exercise, Margaria et al. (1963b) predicted that the rate at which lactic acid is produced, and thus accumulates in blood (and I would add in muscle), is a constant whose value depends on the size of the applied supramaximal power. Experimental validation of this prediction implies linear relationships between blood lactate concentration ([La]b) and exercise time during constant-power supramaximal exercise, with higher slopes the higher is the applied mechanical power. In order to establish these relationships, Margaria et al. (1963b) performed supramaximal exercises of varying intensities while running on a treadmill at various inclines. At each speed and incline, the subjects repeated several trials of progressively increasing duration up to exhaustion. At the end of each trial, the subjects rested and [La]b was measured throughout the recovery period. This led to the demonstration of the predicted linear relationships between [La]b and time, and to the demonstration that, as put 50 years ago, the rate at which lactic acid is produced (in g kg−1 min−1)—actually accumulated, and on average, as more correctly pointed out by di Prampero and Ferretti (1999)—increases linearly with the corresponding metabolic power (in kcal kg−1 min−1) (Fig. 6.1). The intercept on the x-axis of this line was considered indicative of the metabolic power below which no net lactate production occurs (an oversimplification indeed). The slope of the line was taken as a measure of the amount of energy released in vivo by the production of 1 mmol of lactic acid: it amounted to 222 cal g−1 or 84 kJ mol−1. Moreover, assuming that (i) the peak concentration of lactic acid between the 5th and the 8th min of recovery is the same in all body fluids (attainment of equilibrium in lactate concentration) and (ii) the water fractions of the blood and of the whole body are 0.8 and 0.6 respectively, Margaria et al. (1963a, b) deemed possible to estimate the amount of lactic acid produced per kg of body mass.
can derive only from anaerobic energy sources. Apart from the contraction of the obligatory component of the oxygen deficit, which occurs also in the early stages of a supramaximal exercise, reliance is mostly made on anaerobic lactic metabolism. On this basis, on the assumption that the overall metabolic power is directly proportional to the applied mechanical power also during supramaximal exercise, Margaria et al. (1963b) predicted that the rate at which lactic acid is produced, and thus accumulates in blood (and I would add in muscle), is a constant whose value depends on the size of the applied supramaximal power. Experimental validation of this prediction implies linear relationships between blood lactate concentration ([La]b) and exercise time during constant-power supramaximal exercise, with higher slopes the higher is the applied mechanical power. In order to establish these relationships, Margaria et al. (1963b) performed supramaximal exercises of varying intensities while running on a treadmill at various inclines. At each speed and incline, the subjects repeated several trials of progressively increasing duration up to exhaustion. At the end of each trial, the subjects rested and [La]b was measured throughout the recovery period. This led to the demonstration of the predicted linear relationships between [La]b and time, and to the demonstration that, as put 50 years ago, the rate at which lactic acid is produced (in g kg−1 min−1)—actually accumulated, and on average, as more correctly pointed out by di Prampero and Ferretti (1999)—increases linearly with the corresponding metabolic power (in kcal kg−1 min−1) (Fig. 6.1). The intercept on the x-axis of this line was considered indicative of the metabolic power below which no net lactate production occurs (an oversimplification indeed). The slope of the line was taken as a measure of the amount of energy released in vivo by the production of 1 mmol of lactic acid: it amounted to 222 cal g−1 or 84 kJ mol−1. Moreover, assuming that (i) the peak concentration of lactic acid between the 5th and the 8th min of recovery is the same in all body fluids (attainment of equilibrium in lactate concentration) and (ii) the water fractions of the blood and of the whole body are 0.8 and 0.6 respectively, Margaria et al. (1963a, b) deemed possible to estimate the amount of lactic acid produced per kg of body mass.
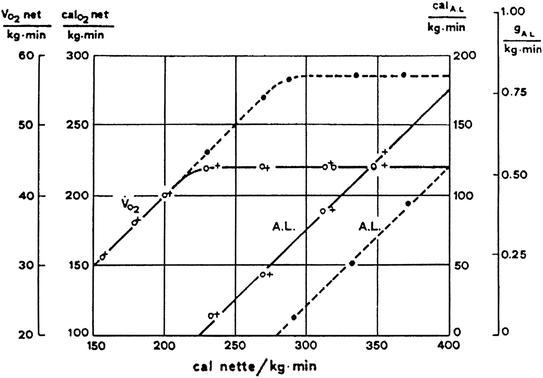
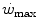 can derive only from anaerobic energy sources. Apart from the contraction of the obligatory component of the oxygen deficit, which occurs also in the early stages of a supramaximal exercise, reliance is mostly made on anaerobic lactic metabolism. On this basis, on the assumption that the overall metabolic power is directly proportional to the applied mechanical power also during supramaximal exercise, Margaria et al. (1963b) predicted that the rate at which lactic acid is produced, and thus accumulates in blood (and I would add in muscle), is a constant whose value depends on the size of the applied supramaximal power. Experimental validation of this prediction implies linear relationships between blood lactate concentration ([La]b) and exercise time during constant-power supramaximal exercise, with higher slopes the higher is the applied mechanical power. In order to establish these relationships, Margaria et al. (1963b) performed supramaximal exercises of varying intensities while running on a treadmill at various inclines. At each speed and incline, the subjects repeated several trials of progressively increasing duration up to exhaustion. At the end of each trial, the subjects rested and [La]b was measured throughout the recovery period. This led to the demonstration of the predicted linear relationships between [La]b and time, and to the demonstration that, as put 50 years ago, the rate at which lactic acid is produced (in g kg−1 min−1)—actually accumulated, and on average, as more correctly pointed out by di Prampero and Ferretti (1999)—increases linearly with the corresponding metabolic power (in kcal kg−1 min−1) (Fig. 6.1). The intercept on the x-axis of this line was considered indicative of the metabolic power below which no net lactate production occurs (an oversimplification indeed). The slope of the line was taken as a measure of the amount of energy released in vivo by the production of 1 mmol of lactic acid: it amounted to 222 cal g−1 or 84 kJ mol−1. Moreover, assuming that (i) the peak concentration of lactic acid between the 5th and the 8th min of recovery is the same in all body fluids (attainment of equilibrium in lactate concentration) and (ii) the water fractions of the blood and of the whole body are 0.8 and 0.6 respectively, Margaria et al. (1963a, b) deemed possible to estimate the amount of lactic acid produced per kg of body mass.
can derive only from anaerobic energy sources. Apart from the contraction of the obligatory component of the oxygen deficit, which occurs also in the early stages of a supramaximal exercise, reliance is mostly made on anaerobic lactic metabolism. On this basis, on the assumption that the overall metabolic power is directly proportional to the applied mechanical power also during supramaximal exercise, Margaria et al. (1963b) predicted that the rate at which lactic acid is produced, and thus accumulates in blood (and I would add in muscle), is a constant whose value depends on the size of the applied supramaximal power. Experimental validation of this prediction implies linear relationships between blood lactate concentration ([La]b) and exercise time during constant-power supramaximal exercise, with higher slopes the higher is the applied mechanical power. In order to establish these relationships, Margaria et al. (1963b) performed supramaximal exercises of varying intensities while running on a treadmill at various inclines. At each speed and incline, the subjects repeated several trials of progressively increasing duration up to exhaustion. At the end of each trial, the subjects rested and [La]b was measured throughout the recovery period. This led to the demonstration of the predicted linear relationships between [La]b and time, and to the demonstration that, as put 50 years ago, the rate at which lactic acid is produced (in g kg−1 min−1)—actually accumulated, and on average, as more correctly pointed out by di Prampero and Ferretti (1999)—increases linearly with the corresponding metabolic power (in kcal kg−1 min−1) (Fig. 6.1). The intercept on the x-axis of this line was considered indicative of the metabolic power below which no net lactate production occurs (an oversimplification indeed). The slope of the line was taken as a measure of the amount of energy released in vivo by the production of 1 mmol of lactic acid: it amounted to 222 cal g−1 or 84 kJ mol−1. Moreover, assuming that (i) the peak concentration of lactic acid between the 5th and the 8th min of recovery is the same in all body fluids (attainment of equilibrium in lactate concentration) and (ii) the water fractions of the blood and of the whole body are 0.8 and 0.6 respectively, Margaria et al. (1963a, b) deemed possible to estimate the amount of lactic acid produced per kg of body mass.
Fig. 6.1
Lactate increase in the body, expressed in g kg−1 min−1 (right ordinate) and net steady-state oxygen consumption per unit of body mass (left ordinate) as a function of power, expressed in cal kg−1 min−1. Full lines refer to non-athletes, dashed lines to athletes. The full line for lactate intercepts the x-axis at a power equal to 220 cal kg−1 min−1, approximately the same value at which the corresponding oxygen consumption line reaches its maximum. According to Margaria et al. (1963b), below this power no lactate was produced and the power was sustained by aerobic metabolism. The lactate line for athletes is displaced to the right. This indicates higher aerobic power and maximal oxygen consumption. The slope of the two lactate lines is the same. Its value indicates an energy “production” of 222 cal g−1 of lactate formed. From Margaria et al. (1963b)
Those results, however, were affected by numerous assumptions, some of which were undemonstrated in those times. Moreover, Margaria et al. (1963b) had the inadvertence of speaking of lactate production rather than lactate accumulation. Therefore, despite the consistency of the evidence that was being progressively accumulated, a stirred debate developed around the concept of energy equivalent of blood lactate accumulation and the energetic significance of lactic acid production. In particular, the concept of equilibrium in lactate distribution was contested by the Scandinavian school of exercise physiology. According to di Prampero and Ferretti (1999), this precluded a widespread practical use of these concepts in vivo, thus finally hindering the progress of our knowledge in the field. I strongly maintain that the energy equivalent of blood lactate accumulation, even though with some cautions and less emphasis than in the past, is and remains a key concept, of extreme utility in the analysis of whole-body energy expenditure during supramaximal exercise (di Prampero 1981).
On the Distribution of Lactate
Margaria et al. (1963b) calculated the rate of lactate production per unit of body mass, on the assumption that the peak [La]b attained between min 5 and 8 of resting recovery after the end of an exercise bout represented the attainment of an equilibrium in lactate concentration in blood and interstitial fluids. This concentration was also assumed to be equal in all body compartments. The latter assumption was demonstrated to be incorrect, as long as (i) lactate anions at equilibrium are mostly located in the extracellular phase (Roos 1975), so that (ii) lactate concentration gradients between intracellular and interstitial fluids exist, and (iii) a passive equilibrium in lactate concentration is not possible. The further characterization of lactate exchange in terms of lactate–proton co-transport shed new light on the equilibria of lactate dynamics (Bonen 2001; Juel 1997, 1998; Juel and Halestrap 1999), even at the subcellular level (Hashimoto and Brooks 2008). Under these circumstances, it is uneasy to calculate the precise amount of lactate that is produced per unit of body mass without a preliminary knowledge of the lactate concentrations in intracellular and interstitial fluids and of their respective fractions. We must also consider that lactate, as it is produced, is also removed, so that the peak [La]b at min 5–8 during recovery is probably less than it would be, where the distribution and mixing of lactate in the body instantaneous. It is easy to state today that the estimate of the energy equivalent of lactate accumulation made by Margaria et al. (1963b) was rough. However, this does not mean that the concept that blood lactate accumulation has an energetic meaning is to be rejected.
Let us assume that peak [La]b reflects indeed the attainment of the equilibrium in lactate distribution in the extracellular compartments. This equilibrium should be independent of the absolute lactate concentrations in blood, and in interstitial and intracellular fluids, each of which can be assimilated to a capacitance that needs to be “discharged”. Thus, after that equilibrium has been attained, two possibilities are given: (i) these capacitances differ in size or in resistance, so that the process of lactate removal is characterized by different time constants, in which case two exponentials are necessary to characterize the function describing lactate removal from the body, or (ii) these two capacitances have the same size and resistance, so that the process of lactate removal from the two body fluids is characterized by equal time constants, in which case a mono-exponential fully describes the entire phenomenon. The body of evidence in favour of the latter hypothesis is important though ancient (Åstrand 1960; di Prampero et al. 1978a, b; Gisolfi et al. 1966; Hermansen and Stensvold 1972; Margaria et al. 1933, 1963b).
A two-compartment model of a different kind, in which one compartment consists of the previously active muscle mass and the other compartment includes the remainder of the volume of blood lactate distribution, was also conceived. This has generated a double-exponential model of lactate removal (Oyono-Enguelle et al. 1993; Zouloumian and Freund 1981), so that some studies have analysed lactate removal after exercise according to this model as well (Freund et al. 1986; Oyono-Enguelle et al. 1990; Taoutaou et al. 1996). This model explains some features of lactate removal immediately after the end of exercise; the first exponential, however, is by far faster than the second, so that the asymptote is quickly attained: therefore, once the equilibrium of lactate concentration in the body has been attained, the first exponential has already reached its asymptote and the further decrease of lactate reflects has the time constant of the second exponential. In other terms, it is as if these two compartments have merged, so that the kinetics of lactate disappearance after recovery min 8 becomes compatible with the classical mono-exponential model.
An elegant quantitative discussion of lactate distribution at equilibrium was carried out by di Prampero (1981). He calculated the ratio of blood to whole-body lactate concentrations at equilibrium, which he demonstrated to be a constant whose value depends on the characteristics of lactate transport across biological membranes, but is independent of the lactate concentrations in the various compartments. Once the equilibrium has been achieved, this constant is invariant with time. Therefore, it could be used for computation of whole-body lactate concentration at the very end of exercise, after determination of the corresponding blood lactate concentration, by back-extrapolation to recovery time 0 of the exponential equation describing the lactate washout from blood during recovery. On this basis, although with a significant degree of approximation, di Prampero et al. (1978b) were able to estimate that the production of 1 mol of lactate during supramaximal exercise can provide about 100 kJ of metabolic energy. Considering the numerous approximations involved, this figure is remarkably close to that obtained by Margaria et al. (1963b).
The Energetics of Supramaximal Exercise
During supramaximal exercise, oxygen consumption may attain its maximum (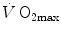 ) in less than 1 min. After this time, we can reasonably assume that the energetic contribution from anaerobic alactic energy sources (Lohmann reaction) desists (di Prampero and Ferretti 1999). So the metabolic power after the initial period is the sum of two terms, one being
) in less than 1 min. After this time, we can reasonably assume that the energetic contribution from anaerobic alactic energy sources (Lohmann reaction) desists (di Prampero and Ferretti 1999). So the metabolic power after the initial period is the sum of two terms, one being 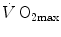 , the second being related to anaerobic lactic metabolism. As a consequence, the general equation takes the following form:
, the second being related to anaerobic lactic metabolism. As a consequence, the general equation takes the following form:
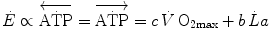
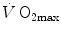 ) in less than 1 min. After this time, we can reasonably assume that the energetic contribution from anaerobic alactic energy sources (Lohmann reaction) desists (di Prampero and Ferretti 1999). So the metabolic power after the initial period is the sum of two terms, one being
) in less than 1 min. After this time, we can reasonably assume that the energetic contribution from anaerobic alactic energy sources (Lohmann reaction) desists (di Prampero and Ferretti 1999). So the metabolic power after the initial period is the sum of two terms, one being 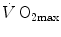 , the second being related to anaerobic lactic metabolism. As a consequence, the general equation takes the following form:
, the second being related to anaerobic lactic metabolism. As a consequence, the general equation takes the following form: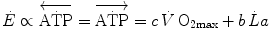
(6.2)
If we express 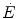 in oxygen equivalents, Eq. (6.2) can be rewritten as follows:
in oxygen equivalents, Eq. (6.2) can be rewritten as follows:
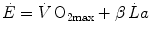
where β is the energy equivalent of blood lactate accumulation, i.e. the amount of energy generated by the accumulation of 1 mol of lactate in blood, and 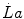 is the rate of blood lactate accumulation. Expressing then Eq. (6.3) relative to
is the rate of blood lactate accumulation. Expressing then Eq. (6.3) relative to 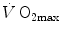 yields
yields
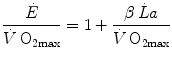
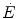 in oxygen equivalents, Eq. (6.2) can be rewritten as follows:
in oxygen equivalents, Eq. (6.2) can be rewritten as follows: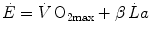
(6.3)
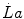 is the rate of blood lactate accumulation. Expressing then Eq. (6.3) relative to
is the rate of blood lactate accumulation. Expressing then Eq. (6.3) relative to 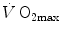 yields
yields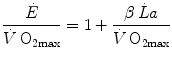
(6.4)
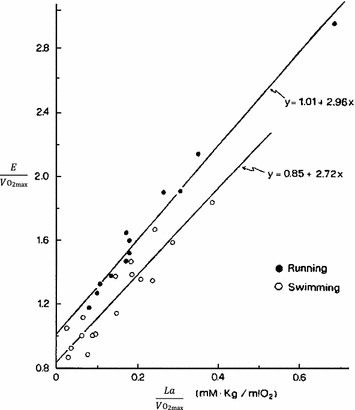
Equation (6.4) allows a comparison of subjects differing in maximal aerobic power and thus working at different levels of supramaximal exercise with different exercise modes. From the data of Margaria et al. (1971a) during treadmill running and Pendergast et al. (1977) during swimming, it was possible to calculate β for both exercise modes. The results, reported in Fig. 6.2, indicate that the energy equivalent of blood lactate accumulation was strikingly similar (3.0 and 2.7 ml O2 kg−1 mM−1 for running and swimming, respectively). These values were essentially confirmed by the analysis of further data obtained under a variety of conditions on humans (Cerretelli et al. 1979; di Prampero et al. 1978b; Margaria et al. 1972), dogs (Cerretelli et al. 1964) and isolated–perfused dog gastrocnemii (Cerretelli et al. 1969). More recently, Capelli and di Prampero (1995) measured the rate of blood lactate accumulation during supramaximal track cycling in a condition in which 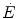 was known. This allowed application of Eq. (6.4), from which β during cycling resulted equal to that for running and swimming. It is nowadays admitted that β is a constant whose value is under any circumstances comprised between 2.7 and 3.3 ml O2 kg−1 mM−1 (di Prampero and Ferretti 1999).
was known. This allowed application of Eq. (6.4), from which β during cycling resulted equal to that for running and swimming. It is nowadays admitted that β is a constant whose value is under any circumstances comprised between 2.7 and 3.3 ml O2 kg−1 mM−1 (di Prampero and Ferretti 1999).
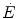 was known. This allowed application of Eq. (6.4), from which β during cycling resulted equal to that for running and swimming. It is nowadays admitted that β is a constant whose value is under any circumstances comprised between 2.7 and 3.3 ml O2 kg−1 mM−1 (di Prampero and Ferretti 1999).
was known. This allowed application of Eq. (6.4), from which β during cycling resulted equal to that for running and swimming. It is nowadays admitted that β is a constant whose value is under any circumstances comprised between 2.7 and 3.3 ml O2 kg−1 mM−1 (di Prampero and Ferretti 1999).
Fig. 6.2
Overall metabolic power (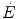 ) as a function of the rate of blood lactate accumulation (
) as a function of the rate of blood lactate accumulation (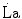 ), both expressed relative to the maximal oxygen consumption (
), both expressed relative to the maximal oxygen consumption (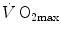 ), in running [full dots, from Margaria et al. (1971a)] and swimming [open dots, from di Prampero et al. (1978b)]. Constant β is obtained from the slopes of the two regression lines
), in running [full dots, from Margaria et al. (1971a)] and swimming [open dots, from di Prampero et al. (1978b)]. Constant β is obtained from the slopes of the two regression lines
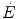 ) as a function of the rate of blood lactate accumulation (
) as a function of the rate of blood lactate accumulation (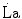 ), both expressed relative to the maximal oxygen consumption (
), both expressed relative to the maximal oxygen consumption (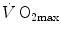 ), in running [full dots, from Margaria et al. (1971a)] and swimming [open dots, from di Prampero et al. (1978b)]. Constant β is obtained from the slopes of the two regression lines
), in running [full dots, from Margaria et al. (1971a)] and swimming [open dots, from di Prampero et al. (1978b)]. Constant β is obtained from the slopes of the two regression linesIt is noteworthy that β is not the energetic equivalent of lactate formation in the working muscles and does not yield any direct information on the stoichiometric relation between lactate formation and ATP resynthesis. It is nevertheless a constant allowing determination of the energy release in the body whenever [La]b increases in blood. As an example, take the case of ramp exercise carried out until exhaustion, which is commonly used in exercise testing. During ramp exercise, the highest work loads are supramaximal, and the more the steeper is the ramp. Thus, part of the ramp is performed at powers above the maximal aerobic power, which are sustained by anaerobic lactic metabolism. If the mechanical efficiency of exercise is known, as is the case for exercise on the cycle ergometer, it would be possible to obtain a good estimate of 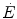 from each value of mechanical power. Solution of Eq. (6.4) for
from each value of mechanical power. Solution of Eq. (6.4) for 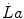 yields
yields
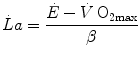
which allows estimating, after assuming a value for 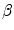 ,
, 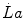 whenever
whenever 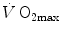 determination.
determination.
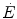 from each value of mechanical power. Solution of Eq. (6.4) for
from each value of mechanical power. Solution of Eq. (6.4) for 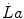 yields
yields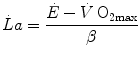
(6.5)
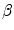 ,
, 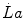 whenever
whenever 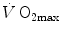 determination.
determination.The Maximal Lactic Power
Since [La]b increases linearly with the exercise intensity, one may predict that it attains a maximum when the energy release from anaerobic lactic metabolism requires the highest possible rate of chemical reactions in the glycolytic pathway. This prediction was demonstrated to be correct during strenuous exercise on the treadmill (Margaria et al. 1964). In fact, subjects ran at 18 km h−1 at slopes up to 25 %, thus performing exercises requiring a metabolic power larger than twice the maximal aerobic power. The results showed that 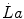 attains an invariant maximal value which does not increase by further increasing the exercise intensity (Fig. 6.3). Moreover, the time after which [La]b starts increasing was found to be shorter the higher is the exercise intensity (displacement on the left of the x-axis intercept of the linear relations in Fig. 6.3). Margaria et al. (1964) proposed that the energy sources for the time that precedes the increase in [La]b were derived from anaerobic alactic metabolism, due to the contraction of the alactic oxygen deficit.
attains an invariant maximal value which does not increase by further increasing the exercise intensity (Fig. 6.3). Moreover, the time after which [La]b starts increasing was found to be shorter the higher is the exercise intensity (displacement on the left of the x-axis intercept of the linear relations in Fig. 6.3). Margaria et al. (1964) proposed that the energy sources for the time that precedes the increase in [La]b were derived from anaerobic alactic metabolism, due to the contraction of the alactic oxygen deficit.
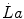 attains an invariant maximal value which does not increase by further increasing the exercise intensity (Fig. 6.3). Moreover, the time after which [La]b starts increasing was found to be shorter the higher is the exercise intensity (displacement on the left of the x-axis intercept of the linear relations in Fig. 6.3). Margaria et al. (1964) proposed that the energy sources for the time that precedes the increase in [La]b were derived from anaerobic alactic metabolism, due to the contraction of the alactic oxygen deficit.
attains an invariant maximal value which does not increase by further increasing the exercise intensity (Fig. 6.3). Moreover, the time after which [La]b starts increasing was found to be shorter the higher is the exercise intensity (displacement on the left of the x-axis intercept of the linear relations in Fig. 6.3). Margaria et al. (1964) proposed that the energy sources for the time that precedes the increase in [La]b were derived from anaerobic alactic metabolism, due to the contraction of the alactic oxygen deficit.
Fig. 6.3
Lactate increase in blood (Δ[La]b) as a function of exercise duration. The four lines refer to four different supramaximal workloads, which were obtained by changing the incline of a treadmill while running at an invariant speed of 18 km h−1. The slope of the lines is equal to the rate of blood lactate accumulation. Since it is unchanged when the incline is increased (the regression equations are reported on the figure), the slope is equal to the maximal rate of lactate accumulation in blood, which is equivalent to the maximal rate of energy release from anaerobic lactic metabolism, or maximal lactic power. From Margaria et al. (1964)
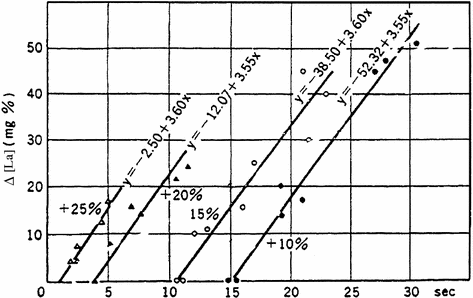
Quantification from these experiments of the maximal lactic power was made possible by the knowledge of β, calculated as described above. On this basis, di Prampero and Ferretti (1999) obtained a value equivalent to some 75 ml O2 kg−1 min−1. This value, which applied to non-athletic young male subjects, corresponded to about 1.5 times the mean 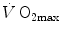 for this type of population.
for this type of population.
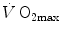 for this type of population.
for this type of population.The complexity of the protocol for the determination of the maximal lactic power is such to restrict a wide use of this test, even for research purposes. So, the studies on the maximal lactic power are extremely scanty. We know that it is higher in power athletes than in non-athletes (Hermansen 1971) and that it is reduced after altitude acclimatization (Grassi et al. 1995). Some relation to the muscle fibre composition of lower limbs must exist, so that it would be easy to predict a low maximal lactic power in endurance athletes, possibly less than their maximal aerobic power. The loss of muscle mass with ageing allows predicting its decrease at older ages. Sport practice demonstrates that it can be trained—interval training was introduced to this purpose indeed—but no study of the effects of specific training on the maximal lactic power was ever carried out.
The Maximal Lactic Capacity
Knowledge of β, of the overall energy requirement of the exercise, and of the time constant of 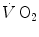 kinetics, which determines the contraction of the alactic oxygen deficit (23 s, Binzoni et al. 1992), allows computation, after measurement of peak [La]b at exhaustion and of
kinetics, which determines the contraction of the alactic oxygen deficit (23 s, Binzoni et al. 1992), allows computation, after measurement of peak [La]b at exhaustion and of 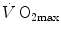 , of the amount of energy that can be derived from the full utilization of anaerobic lactic energy stores, or maximal lactic capacity. This ranges, for continuous supramaximal exercise, between 45 and 55 ml O2 kg−1 (di Prampero and Ferretti 1999), corresponding to a peak [La]b at exhaustion between 14 and 17 mM. It is greater the larger is the active muscle mass, higher in power athletes and lower in marathon runners than in non-athletic subjects (Komi et al. 1977; Nummela et al. 1996; Tam et al. 2012). It may be as twice as high during intermittent exercise (Osnes and Hermansen 1972) and is decreased in chronic hypoxia (Cerretelli 1967; Cerretelli and Binzoni 1990).
, of the amount of energy that can be derived from the full utilization of anaerobic lactic energy stores, or maximal lactic capacity. This ranges, for continuous supramaximal exercise, between 45 and 55 ml O2 kg−1 (di Prampero and Ferretti 1999), corresponding to a peak [La]b at exhaustion between 14 and 17 mM. It is greater the larger is the active muscle mass, higher in power athletes and lower in marathon runners than in non-athletic subjects (Komi et al. 1977; Nummela et al. 1996; Tam et al. 2012). It may be as twice as high during intermittent exercise (Osnes and Hermansen 1972) and is decreased in chronic hypoxia (Cerretelli 1967; Cerretelli and Binzoni 1990).
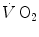 kinetics, which determines the contraction of the alactic oxygen deficit (23 s, Binzoni et al. 1992), allows computation, after measurement of peak [La]b at exhaustion and of
kinetics, which determines the contraction of the alactic oxygen deficit (23 s, Binzoni et al. 1992), allows computation, after measurement of peak [La]b at exhaustion and of 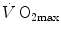 , of the amount of energy that can be derived from the full utilization of anaerobic lactic energy stores, or maximal lactic capacity. This ranges, for continuous supramaximal exercise, between 45 and 55 ml O2 kg−1 (di Prampero and Ferretti 1999), corresponding to a peak [La]b at exhaustion between 14 and 17 mM. It is greater the larger is the active muscle mass, higher in power athletes and lower in marathon runners than in non-athletic subjects (Komi et al. 1977; Nummela et al. 1996; Tam et al. 2012). It may be as twice as high during intermittent exercise (Osnes and Hermansen 1972) and is decreased in chronic hypoxia (Cerretelli 1967; Cerretelli and Binzoni 1990).
, of the amount of energy that can be derived from the full utilization of anaerobic lactic energy stores, or maximal lactic capacity. This ranges, for continuous supramaximal exercise, between 45 and 55 ml O2 kg−1 (di Prampero and Ferretti 1999), corresponding to a peak [La]b at exhaustion between 14 and 17 mM. It is greater the larger is the active muscle mass, higher in power athletes and lower in marathon runners than in non-athletic subjects (Komi et al. 1977; Nummela et al. 1996; Tam et al. 2012). It may be as twice as high during intermittent exercise (Osnes and Hermansen 1972) and is decreased in chronic hypoxia (Cerretelli 1967; Cerretelli and Binzoni 1990).Lactate accumulation in muscle is obviously associated with a simultaneous increase in H+ concentration in the active muscle mass, which may well limit maximal lactic capacity. This depends also on the buffer characteristics of muscle fibres and blood, and on the rate at which lactate can be removed from muscles. If this is so, then the higher lactic capacity during intermittent exercise is a consequence of the effects of recovery periods—no matter whether active or resting—on H+ concentration in muscle fibres. In fact H+ inhibit glycolysis, stopping the glycolytic energy flow when given lactate concentrations are attained: these would correspond, at the end of continuous exhausting exercise, to the [La]b values reported above. The slight decrease in muscle lactate during the recovery phase of intermittent exercise allows further lactate production in the successive supramaximal bout, whence the attainment of higher [La]b values, and so of a larger lactic capacity, in intermittent than in continuous exercise, thus explaining the results of Osnes and Hermansen (1972). In sport practice, this reasoning provides the physiological explanation of how and why during interval training sessions athletes can tolerate numerous extremely high power repetitions, otherwise incompatible with the findings at the end of supramaximal continuous constant-load exercise in the laboratory.
The maximal lactic capacity is unchanged in acute hypoxia, but progressively decreases in chronic hypoxia (Cerretelli 1967). The reduction of maximal lactic capacity in chronic hypoxia, an intriguing aspect of altitude acclimatization, is reversible after return to sea level (Cerretelli and Binzoni 1990) and is unaffected by bicarbonate loading (Kayser et al. 1993). These findings are not due to changes in the activity of glycolytic enzymes, which is unaffected by chronic hypoxia (Cerretelli and Hoppeler 1996). The ensemble of these results was considered contradictory, so that this phenomenon was called the lactate paradox. Although the maximal [La]b is lower the higher is the altitude at which acclimatization has occurred, the ability of muscle fibres to produce lactate seems unaffected by the acclimatization process: what appears to be reduced is the net flux of lactate from the contracting muscle mass to the blood (Brooks et al. 1998). This led to the hypothesis that the lactate paradox might follow a fall of lactate transport outside muscle fibres, perhaps due to reduced activity of the lactate–proton co-transporter. If the acclimatization process is prolonged beyond 6 weeks, maximal lactic capacity progressively recovers, until the differences between acute and chronic hypoxia disappear (Lundby et al. 2000), suggesting that the lactate paradox may be a transient phenomenon. In fact the rate of lactate outflow from muscle fibres to blood increases with time at altitude, which implies also an increase in the rate of lactate removal from blood by lactate metabolizing organs, such as liver, brain, kidneys and heart, and eventually also non-contracting muscles. If the hypothesis of a reduced activity of the lactate–proton co-transporter in chronic hypoxia is correct, then the recovery of the maximal lactic capacity after the 6 week at altitude implies up-regulation of co-transporter synthesis (van Hall et al. 2001). Such modification requires alterations of the regulation of protein synthesis, and thus necessarily has a slow kinetics. If this is so, then there would be dissociation between co-transporter inhibition and increased co-transporter synthesis, which would explain the lactate paradox as a transitory phenomenon. However, the lactate paradox was observed also in populations living permanently at altitude, which undergo lifelong hypoxic stimulation: if the lactate paradox was transitory, these populations would not be affected by it. Clearly enough, our understanding of the lactate paradox is still incomplete.
The P/La Ratio
Constant β is an epiphenomenon of the actual phenomenon that is the amount of energy released by anaerobic lactic metabolism through ATP resynthesis, the latter being the actual source of energy for muscular contraction. Thus, knowledge of the amount of ATP resynthesized from the accumulation of 1 mol of lactate in the contracting muscle mass is a key element for our understanding of the energetics of muscular exercise. This is the P/La ratio, i.e. constant b in Eq. (6.2), which is related to β through another constant γ, the dimension of which is moles of ATP resynthesized per J of energy released (reciprocal of the amount of energy that is necessary to resynthesize one mole of ATP). Computation of the P/La ratio from the measurement of blood lactate accumulation in humans is impossible because we do not know the value of γ. The P/La ratio was calculated from data obtained in isolated–perfused dog gastrocnemii with blood flow occlusion under supramaximal stimulation (di Prampero et al. 1978a). Under these conditions, the amount of energy derived from muscle oxygen stores is negligible, so that the general equation reduces to
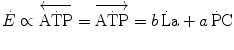
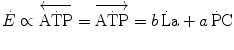
(6.6)
Since phosphocreatine concentration, which is invariant at rest, goes down to almost 0 mM at the end of an exhaustive series of supramaximal stimulations (Cerretelli et al. 1969), the energy provided by anaerobic alactic metabolism in the transition from rest to stimulation can be considered constant. As a consequence, the total enthalpy change (ΔH, work plus heat) under those conditions is given by
![$$ \Delta H = H_{\text{Al}} + X_{\text{La}} [{\text{La}}]_{{m}} $$](/wp-content/uploads/2016/09/A322139_1_En_6_Chapter_Equ7.gif)
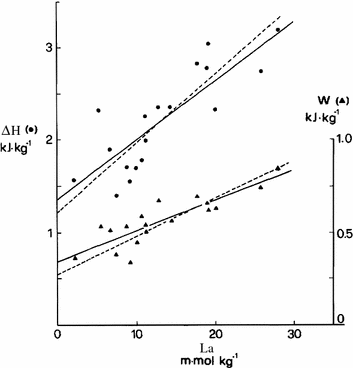
where H Al is the enthalpy change due to anaerobic alactic metabolism, Χ La is the enthalpy change due to the formation of 1 mol of lactate at the output of the glycolytic pathway, and [La] m is the overall amount of lactate produced (no lactate removal in these circumstances). Equation (6.7) implies a linear relation between ΔH and [La] m , with slope equal to Χ La and y-intercept equal to H Al. The linear regression of the relation established by di Prampero et al. (1978a), reported in Fig. 6.4, yielded Χ La = 76 kJ mol−1 and H Al = 1.2 kJ kg−1. Moreover, if the mechanical efficiency of muscular contraction under these conditions was invariant, also the relationship between work (W) and [La] m (Fig. 6.4, right ordinate) ought to be linear, with slope indicating the work done per mole of lactate produced, for which a value of 20 kJ mol−1 was obtained. The P/La ratio is given by the further ratio of this last value to the W per mole of ATP split (W*~p ), which was found to range between 16 and 19 kJ mol−1 (Cerretelli et al. 1969, 1972; Cerretelli and di Prampero 1988; Ferretti et al. 1987). As a consequence, the P/La ratio ranges between 1.25 and 1.05 mol of phosphate per mole of lactate, which is slightly less than the value of 1.5 predicted from stoichiometry. These values would be compatible with a range of values for the enthalpy change of ATP hydrolysis comprised between 60 and 72 kJ mol−1, which is significantly higher than what one would expect from the value of 50 kJ mol−1 that can be calculated assuming a P/La ratio equal to that in vitro.
![$$ \Delta H = H_{\text{Al}} + X_{\text{La}} [{\text{La}}]_{{m}} $$](/wp-content/uploads/2016/09/A322139_1_En_6_Chapter_Equ7.gif)
(6.7)

Fig. 6.4




Enthalpy change (ΔH, in kJ kg−1, left ordinate, dots) and work (W, in kJ kg−1, right ordinate, triangles) as a function of lactate formed (La, mmol kg−1) during supramaximal stimulation of isolated–perfused dog gastrocnemius in anoxia. The slopes of the lines indicate, respectively, the energy released by (top lines) and the work performed by (bottom lines) a unit of lactate formed during contraction. Continuous lines are regression lines obtained with the classical least-square method; dashed lines are regression lines obtained with Brace method. From di Prampero et al. (1978a)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



