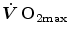Limitation
Abstract
As soon as the concept of maximal oxygen consumption 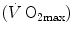 was created, it was clear that
was created, it was clear that 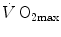 was limited somewhere along the respiratory system. The quest for the single factor limiting
was limited somewhere along the respiratory system. The quest for the single factor limiting 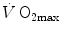 went on for long, with highly contradictory outcomes. The way of looking at
went on for long, with highly contradictory outcomes. The way of looking at 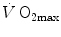 limitation, however, changed drastically some 30 years ago. The resumption of the oxygen cascade theory as a tool for a holistic description of the respiratory system led to the development of multifactorial models of
limitation, however, changed drastically some 30 years ago. The resumption of the oxygen cascade theory as a tool for a holistic description of the respiratory system led to the development of multifactorial models of 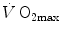 limitation. Two such models are currently available, one created by Pietro Enrico di Prampero and the other by Peter Wagner. These models are described in detail and criticized. The evidence supporting the predictions generated by the two models is presented. Demonstration is provided that the two models converge indeed on the same conclusion, namely that most of the limitation to
limitation. Two such models are currently available, one created by Pietro Enrico di Prampero and the other by Peter Wagner. These models are described in detail and criticized. The evidence supporting the predictions generated by the two models is presented. Demonstration is provided that the two models converge indeed on the same conclusion, namely that most of the limitation to 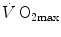 in normoxia is provided by cardiovascular oxygen transport. However, the same models show that the role of peripheral oxygen diffusion and utilization as limiting factors is such that it cannot be neglected. The special case of
in normoxia is provided by cardiovascular oxygen transport. However, the same models show that the role of peripheral oxygen diffusion and utilization as limiting factors is such that it cannot be neglected. The special case of 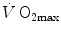 in hypoxia is then presented, and the effects of a nonlinear oxygen equilibrium curve are discussed. It is acknowledged that as long as we operate on the flat portion of the oxygen equilibrium curve, the lungs do not limit
in hypoxia is then presented, and the effects of a nonlinear oxygen equilibrium curve are discussed. It is acknowledged that as long as we operate on the flat portion of the oxygen equilibrium curve, the lungs do not limit 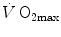 , but as soon as the steep part of the curve is attained, the lungs take over a significant fraction of
, but as soon as the steep part of the curve is attained, the lungs take over a significant fraction of 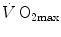 limitation. Finally, the case of prolonged bed rest is discussed as an example of
limitation. Finally, the case of prolonged bed rest is discussed as an example of 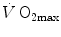 changes induced by simultaneous multiple modifications occurring at various levels along the respiratory system.
changes induced by simultaneous multiple modifications occurring at various levels along the respiratory system.
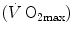 was created, it was clear that
was created, it was clear that 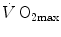 was limited somewhere along the respiratory system. The quest for the single factor limiting
was limited somewhere along the respiratory system. The quest for the single factor limiting 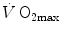 went on for long, with highly contradictory outcomes. The way of looking at
went on for long, with highly contradictory outcomes. The way of looking at 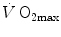 limitation, however, changed drastically some 30 years ago. The resumption of the oxygen cascade theory as a tool for a holistic description of the respiratory system led to the development of multifactorial models of
limitation, however, changed drastically some 30 years ago. The resumption of the oxygen cascade theory as a tool for a holistic description of the respiratory system led to the development of multifactorial models of 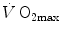 limitation. Two such models are currently available, one created by Pietro Enrico di Prampero and the other by Peter Wagner. These models are described in detail and criticized. The evidence supporting the predictions generated by the two models is presented. Demonstration is provided that the two models converge indeed on the same conclusion, namely that most of the limitation to
limitation. Two such models are currently available, one created by Pietro Enrico di Prampero and the other by Peter Wagner. These models are described in detail and criticized. The evidence supporting the predictions generated by the two models is presented. Demonstration is provided that the two models converge indeed on the same conclusion, namely that most of the limitation to 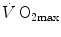 in normoxia is provided by cardiovascular oxygen transport. However, the same models show that the role of peripheral oxygen diffusion and utilization as limiting factors is such that it cannot be neglected. The special case of
in normoxia is provided by cardiovascular oxygen transport. However, the same models show that the role of peripheral oxygen diffusion and utilization as limiting factors is such that it cannot be neglected. The special case of 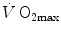 in hypoxia is then presented, and the effects of a nonlinear oxygen equilibrium curve are discussed. It is acknowledged that as long as we operate on the flat portion of the oxygen equilibrium curve, the lungs do not limit
in hypoxia is then presented, and the effects of a nonlinear oxygen equilibrium curve are discussed. It is acknowledged that as long as we operate on the flat portion of the oxygen equilibrium curve, the lungs do not limit 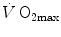 , but as soon as the steep part of the curve is attained, the lungs take over a significant fraction of
, but as soon as the steep part of the curve is attained, the lungs take over a significant fraction of 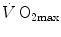 limitation. Finally, the case of prolonged bed rest is discussed as an example of
limitation. Finally, the case of prolonged bed rest is discussed as an example of 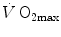 changes induced by simultaneous multiple modifications occurring at various levels along the respiratory system.
changes induced by simultaneous multiple modifications occurring at various levels along the respiratory system.Introduction
The concept of maximal oxygen consumption 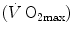 was created when it was observed that the linear relationship between oxygen uptake
was created when it was observed that the linear relationship between oxygen uptake 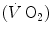 and mechanical power (
and mechanical power (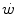 ) attains a plateau which cannot be overcome despite further increases of
) attains a plateau which cannot be overcome despite further increases of 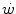 (Herbst 1928; Hill and Lupton 1923) (Fig. 4.1). The
(Herbst 1928; Hill and Lupton 1923) (Fig. 4.1). The 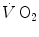 plateau implied limitation of oxygen flow at some levels along the respiratory system. The quest for the factors that limit
plateau implied limitation of oxygen flow at some levels along the respiratory system. The quest for the factors that limit 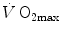 has not ceased ever since. For a long time, the discussion on
has not ceased ever since. For a long time, the discussion on 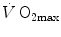 limitation focused on the identification of a single limiting step. A long-lasting debate between two opposed fields, that of central (cardiovascular) limitation and that of peripheral (muscular) limitation characterized 50 years of research in exercise physiology, without significant synthesis.
limitation focused on the identification of a single limiting step. A long-lasting debate between two opposed fields, that of central (cardiovascular) limitation and that of peripheral (muscular) limitation characterized 50 years of research in exercise physiology, without significant synthesis.
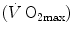 was created when it was observed that the linear relationship between oxygen uptake
was created when it was observed that the linear relationship between oxygen uptake 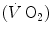 and mechanical power (
and mechanical power (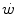 ) attains a plateau which cannot be overcome despite further increases of
) attains a plateau which cannot be overcome despite further increases of 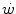 (Herbst 1928; Hill and Lupton 1923) (Fig. 4.1). The
(Herbst 1928; Hill and Lupton 1923) (Fig. 4.1). The 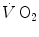 plateau implied limitation of oxygen flow at some levels along the respiratory system. The quest for the factors that limit
plateau implied limitation of oxygen flow at some levels along the respiratory system. The quest for the factors that limit 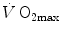 has not ceased ever since. For a long time, the discussion on
has not ceased ever since. For a long time, the discussion on 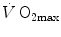 limitation focused on the identification of a single limiting step. A long-lasting debate between two opposed fields, that of central (cardiovascular) limitation and that of peripheral (muscular) limitation characterized 50 years of research in exercise physiology, without significant synthesis.
limitation focused on the identification of a single limiting step. A long-lasting debate between two opposed fields, that of central (cardiovascular) limitation and that of peripheral (muscular) limitation characterized 50 years of research in exercise physiology, without significant synthesis.
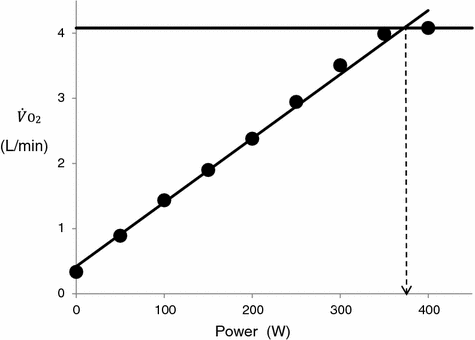
Fig. 4.1
An example of a relationship between oxygen uptake (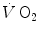 ) and power during a classical discontinuous protocol for
) and power during a classical discontinuous protocol for 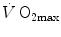 measurements. The reported data refer to a trained top-level cyclist tested in Geneva. The line through the points is the regression line calculated on the submaximal
measurements. The reported data refer to a trained top-level cyclist tested in Geneva. The line through the points is the regression line calculated on the submaximal 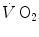 values. The horizontal line indicates the
values. The horizontal line indicates the 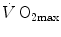 plateau. The vertical dashed arrow indicates the maximal aerobic power. From Ferretti (2014)
plateau. The vertical dashed arrow indicates the maximal aerobic power. From Ferretti (2014)
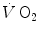 ) and power during a classical discontinuous protocol for
) and power during a classical discontinuous protocol for 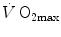 measurements. The reported data refer to a trained top-level cyclist tested in Geneva. The line through the points is the regression line calculated on the submaximal
measurements. The reported data refer to a trained top-level cyclist tested in Geneva. The line through the points is the regression line calculated on the submaximal 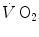 values. The horizontal line indicates the
values. The horizontal line indicates the 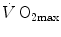 plateau. The vertical dashed arrow indicates the maximal aerobic power. From Ferretti (2014)
plateau. The vertical dashed arrow indicates the maximal aerobic power. From Ferretti (2014)A revolution in the approach to the subject of 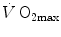 limitation occurred after Taylor and Weibel (1981) resumed the oxygen cascade theory as a tool for describing oxygen transfer from ambient air to the mitochondria in mammals. Although their aim was to analyse the structural constraints of respiratory systems under maximal stress in animals encompassing a wide range of body size, that idea brought some exercise physiologists to consider the multiple factors that contribute to
limitation occurred after Taylor and Weibel (1981) resumed the oxygen cascade theory as a tool for describing oxygen transfer from ambient air to the mitochondria in mammals. Although their aim was to analyse the structural constraints of respiratory systems under maximal stress in animals encompassing a wide range of body size, that idea brought some exercise physiologists to consider the multiple factors that contribute to 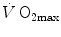 limitation under a holistic perspective. The quest for the single limiting step came to an end and the way to the creation of the multifactorial models of
limitation under a holistic perspective. The quest for the single limiting step came to an end and the way to the creation of the multifactorial models of 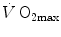 limitation (di Prampero 1985, 2003; di Prampero and Ferretti 1990; Ferretti and di Prampero 1995; Wagner 1992, 1993, 1996a, b). These models have characterized the last 20 years of debate on this issue.
limitation (di Prampero 1985, 2003; di Prampero and Ferretti 1990; Ferretti and di Prampero 1995; Wagner 1992, 1993, 1996a, b). These models have characterized the last 20 years of debate on this issue. 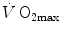 and the multifactorial models of
and the multifactorial models of 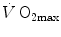 limitation are the objects of this chapter.
limitation are the objects of this chapter.
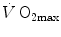 limitation occurred after Taylor and Weibel (1981) resumed the oxygen cascade theory as a tool for describing oxygen transfer from ambient air to the mitochondria in mammals. Although their aim was to analyse the structural constraints of respiratory systems under maximal stress in animals encompassing a wide range of body size, that idea brought some exercise physiologists to consider the multiple factors that contribute to
limitation occurred after Taylor and Weibel (1981) resumed the oxygen cascade theory as a tool for describing oxygen transfer from ambient air to the mitochondria in mammals. Although their aim was to analyse the structural constraints of respiratory systems under maximal stress in animals encompassing a wide range of body size, that idea brought some exercise physiologists to consider the multiple factors that contribute to 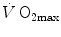 limitation under a holistic perspective. The quest for the single limiting step came to an end and the way to the creation of the multifactorial models of
limitation under a holistic perspective. The quest for the single limiting step came to an end and the way to the creation of the multifactorial models of 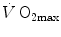 limitation (di Prampero 1985, 2003; di Prampero and Ferretti 1990; Ferretti and di Prampero 1995; Wagner 1992, 1993, 1996a, b). These models have characterized the last 20 years of debate on this issue.
limitation (di Prampero 1985, 2003; di Prampero and Ferretti 1990; Ferretti and di Prampero 1995; Wagner 1992, 1993, 1996a, b). These models have characterized the last 20 years of debate on this issue. 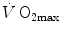 and the multifactorial models of
and the multifactorial models of 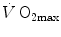 limitation are the objects of this chapter.
limitation are the objects of this chapter.The Unifactorial Vision of 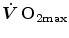 Limitation
Limitation
The descriptive physiology of 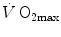 has been the object of thousands of papers, the results of which have been summarized in numerous review articles (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Cerretelli and Hoppeler 1996; Ferretti 2014; Jones and Lindstedt 1993; Lacour and Flandrois 1977; Levine 2008; Saltin 1977; Scheuer and Tipton 1977; Stamford 1988; Taylor 1987; Tesch 1985; Weibel 1987; Weibel et al. 1992). In short,
has been the object of thousands of papers, the results of which have been summarized in numerous review articles (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Cerretelli and Hoppeler 1996; Ferretti 2014; Jones and Lindstedt 1993; Lacour and Flandrois 1977; Levine 2008; Saltin 1977; Scheuer and Tipton 1977; Stamford 1988; Taylor 1987; Tesch 1985; Weibel 1987; Weibel et al. 1992). In short, 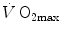 is (i) up to twice higher in endurance athletes than in sedentary individuals; (ii) higher in men than in women; (iii) decreased by ageing, with athletes maintaining higher
is (i) up to twice higher in endurance athletes than in sedentary individuals; (ii) higher in men than in women; (iii) decreased by ageing, with athletes maintaining higher 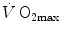 values than non-athletic individuals along the entire lifespan; (iv) reduced by inactivity (e.g. bed rest) or by hypoxia; (v) increased by endurance training, whether with continuous or interval-training protocols, depending on the overall training volume. Training also slows down the
values than non-athletic individuals along the entire lifespan; (iv) reduced by inactivity (e.g. bed rest) or by hypoxia; (v) increased by endurance training, whether with continuous or interval-training protocols, depending on the overall training volume. Training also slows down the 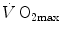 decline with age.
decline with age.
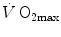 has been the object of thousands of papers, the results of which have been summarized in numerous review articles (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Cerretelli and Hoppeler 1996; Ferretti 2014; Jones and Lindstedt 1993; Lacour and Flandrois 1977; Levine 2008; Saltin 1977; Scheuer and Tipton 1977; Stamford 1988; Taylor 1987; Tesch 1985; Weibel 1987; Weibel et al. 1992). In short,
has been the object of thousands of papers, the results of which have been summarized in numerous review articles (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Cerretelli and Hoppeler 1996; Ferretti 2014; Jones and Lindstedt 1993; Lacour and Flandrois 1977; Levine 2008; Saltin 1977; Scheuer and Tipton 1977; Stamford 1988; Taylor 1987; Tesch 1985; Weibel 1987; Weibel et al. 1992). In short, 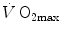 is (i) up to twice higher in endurance athletes than in sedentary individuals; (ii) higher in men than in women; (iii) decreased by ageing, with athletes maintaining higher
is (i) up to twice higher in endurance athletes than in sedentary individuals; (ii) higher in men than in women; (iii) decreased by ageing, with athletes maintaining higher 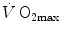 values than non-athletic individuals along the entire lifespan; (iv) reduced by inactivity (e.g. bed rest) or by hypoxia; (v) increased by endurance training, whether with continuous or interval-training protocols, depending on the overall training volume. Training also slows down the
values than non-athletic individuals along the entire lifespan; (iv) reduced by inactivity (e.g. bed rest) or by hypoxia; (v) increased by endurance training, whether with continuous or interval-training protocols, depending on the overall training volume. Training also slows down the 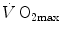 decline with age.
decline with age.These effects on 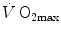 are associated with consensual and quantitatively similar changes in maximal cardiac output (
are associated with consensual and quantitatively similar changes in maximal cardiac output (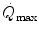 ) (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Clausen 1977; Ekblom et al. 1968). Also the effects of acute manipulations of the cardiovascular oxygen transport system on
) (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Clausen 1977; Ekblom et al. 1968). Also the effects of acute manipulations of the cardiovascular oxygen transport system on 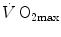 were widely investigated.
were widely investigated. 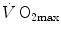 was found to be lower in acute anaemia than in normaemia (Celsing et al. 1987; Krip et al. 1997; Woodson et al. 1978) and higher in acute polycythaemia than in normaemia (Buick et al. 1980; Celsing et al. 1987; Ekblom et al. 1975, 1976; Spriet et al. 1986; Turner et al. 1993), and after erythropoietin administration (Russell et al. 2002; Thomsen et al. 2007).
was found to be lower in acute anaemia than in normaemia (Celsing et al. 1987; Krip et al. 1997; Woodson et al. 1978) and higher in acute polycythaemia than in normaemia (Buick et al. 1980; Celsing et al. 1987; Ekblom et al. 1975, 1976; Spriet et al. 1986; Turner et al. 1993), and after erythropoietin administration (Russell et al. 2002; Thomsen et al. 2007). 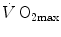 is reduced also when small quantities of carbon monoxide are added to inspired air (Ekblom and Huot 1972; Pirnay et al. 1971; Vogel and Gleser 1972). The relationship between
is reduced also when small quantities of carbon monoxide are added to inspired air (Ekblom and Huot 1972; Pirnay et al. 1971; Vogel and Gleser 1972). The relationship between 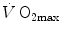 and
and 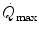 is linear and highly significant (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987), as is that between
is linear and highly significant (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987), as is that between 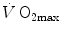 and leg blood flow during single-leg extension exercise (Calbet et al. 2004, 2007; Richardson et al. 1995b). Finally, if sufficient blood flow is delivered to the contracting muscle mass, specific muscle
and leg blood flow during single-leg extension exercise (Calbet et al. 2004, 2007; Richardson et al. 1995b). Finally, if sufficient blood flow is delivered to the contracting muscle mass, specific muscle 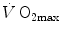 can increase well above the levels attained at maximal exercise in normal blood flow condition (Andersen and Saltin 1985; Richardson et al. 1995a; Rowell et al. 1986). On this basis, a large number of exercise physiologists concluded that at least during exercise with large muscle groups, the single factor limiting
can increase well above the levels attained at maximal exercise in normal blood flow condition (Andersen and Saltin 1985; Richardson et al. 1995a; Rowell et al. 1986). On this basis, a large number of exercise physiologists concluded that at least during exercise with large muscle groups, the single factor limiting 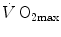 is cardiovascular oxygen transport (Blomqvist and Saltin 1983; Clausen 1977; Ekblom 1969, 1986; Mitchell and Blomqvist 1971; Rowell 1974; Saltin and Rowell 1980; Saltin and Strange 1992; Scheuer and Tipton 1977; Sutton 1992).
is cardiovascular oxygen transport (Blomqvist and Saltin 1983; Clausen 1977; Ekblom 1969, 1986; Mitchell and Blomqvist 1971; Rowell 1974; Saltin and Rowell 1980; Saltin and Strange 1992; Scheuer and Tipton 1977; Sutton 1992).
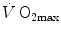 are associated with consensual and quantitatively similar changes in maximal cardiac output (
are associated with consensual and quantitatively similar changes in maximal cardiac output (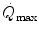 ) (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Clausen 1977; Ekblom et al. 1968). Also the effects of acute manipulations of the cardiovascular oxygen transport system on
) (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987; Clausen 1977; Ekblom et al. 1968). Also the effects of acute manipulations of the cardiovascular oxygen transport system on 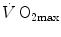 were widely investigated.
were widely investigated. 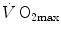 was found to be lower in acute anaemia than in normaemia (Celsing et al. 1987; Krip et al. 1997; Woodson et al. 1978) and higher in acute polycythaemia than in normaemia (Buick et al. 1980; Celsing et al. 1987; Ekblom et al. 1975, 1976; Spriet et al. 1986; Turner et al. 1993), and after erythropoietin administration (Russell et al. 2002; Thomsen et al. 2007).
was found to be lower in acute anaemia than in normaemia (Celsing et al. 1987; Krip et al. 1997; Woodson et al. 1978) and higher in acute polycythaemia than in normaemia (Buick et al. 1980; Celsing et al. 1987; Ekblom et al. 1975, 1976; Spriet et al. 1986; Turner et al. 1993), and after erythropoietin administration (Russell et al. 2002; Thomsen et al. 2007). 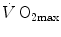 is reduced also when small quantities of carbon monoxide are added to inspired air (Ekblom and Huot 1972; Pirnay et al. 1971; Vogel and Gleser 1972). The relationship between
is reduced also when small quantities of carbon monoxide are added to inspired air (Ekblom and Huot 1972; Pirnay et al. 1971; Vogel and Gleser 1972). The relationship between 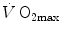 and
and 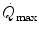 is linear and highly significant (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987), as is that between
is linear and highly significant (Blomqvist and Saltin 1983; Cerretelli and di Prampero 1987), as is that between 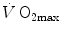 and leg blood flow during single-leg extension exercise (Calbet et al. 2004, 2007; Richardson et al. 1995b). Finally, if sufficient blood flow is delivered to the contracting muscle mass, specific muscle
and leg blood flow during single-leg extension exercise (Calbet et al. 2004, 2007; Richardson et al. 1995b). Finally, if sufficient blood flow is delivered to the contracting muscle mass, specific muscle 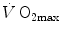 can increase well above the levels attained at maximal exercise in normal blood flow condition (Andersen and Saltin 1985; Richardson et al. 1995a; Rowell et al. 1986). On this basis, a large number of exercise physiologists concluded that at least during exercise with large muscle groups, the single factor limiting
can increase well above the levels attained at maximal exercise in normal blood flow condition (Andersen and Saltin 1985; Richardson et al. 1995a; Rowell et al. 1986). On this basis, a large number of exercise physiologists concluded that at least during exercise with large muscle groups, the single factor limiting 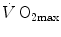 is cardiovascular oxygen transport (Blomqvist and Saltin 1983; Clausen 1977; Ekblom 1969, 1986; Mitchell and Blomqvist 1971; Rowell 1974; Saltin and Rowell 1980; Saltin and Strange 1992; Scheuer and Tipton 1977; Sutton 1992).
is cardiovascular oxygen transport (Blomqvist and Saltin 1983; Clausen 1977; Ekblom 1969, 1986; Mitchell and Blomqvist 1971; Rowell 1974; Saltin and Rowell 1980; Saltin and Strange 1992; Scheuer and Tipton 1977; Sutton 1992).However, focusing on active muscles showed that (i) the smaller is the active muscle mass, the lower is 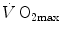 (Åstrand and Saltin 1961; Bergh et al. 1976; Davies and Sargeant 1974; Secher et al. 1974); (ii) specific endurance training of one leg increases
(Åstrand and Saltin 1961; Bergh et al. 1976; Davies and Sargeant 1974; Secher et al. 1974); (ii) specific endurance training of one leg increases 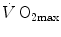 during exercise with that leg only (Saltin et al. 1976); (iii) endurance athletes have a greater fraction of oxidative type I muscle fibres, a greater muscle capillary density and a higher activity of muscle oxidative enzymes than sedentary individuals (Brodal et al. 1977; Costill et al. 1976; Gollnick et al. 1972; Howald 1982; Tesch and Karlsson 1985; Zumstein et al. 1983); (iv) muscle capillary supply, muscle mitochondrial volume and muscle oxidative enzyme activities are increased by physical training (Andersen and Henriksson 1977; Gollnick et al. 1973; Henriksson 1977; Holloszy and Coyle 1984; Hoppeler et al. 1985; Howald et al. 1985; Ingjer 1979) and decreased by prolonged inactivity (Berg et al. 1993; Booth 1982; Hikida et al. 1989). Furthermore, and most importantly, the
during exercise with that leg only (Saltin et al. 1976); (iii) endurance athletes have a greater fraction of oxidative type I muscle fibres, a greater muscle capillary density and a higher activity of muscle oxidative enzymes than sedentary individuals (Brodal et al. 1977; Costill et al. 1976; Gollnick et al. 1972; Howald 1982; Tesch and Karlsson 1985; Zumstein et al. 1983); (iv) muscle capillary supply, muscle mitochondrial volume and muscle oxidative enzyme activities are increased by physical training (Andersen and Henriksson 1977; Gollnick et al. 1973; Henriksson 1977; Holloszy and Coyle 1984; Hoppeler et al. 1985; Howald et al. 1985; Ingjer 1979) and decreased by prolonged inactivity (Berg et al. 1993; Booth 1982; Hikida et al. 1989). Furthermore, and most importantly, the 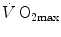 of altitude-acclimatized subjects who are staying in chronic hypoxia, after sudden exposure to normoxic gas mixtures, does not return to the pre-acclimatization levels (Cerretelli 1976). On these bases, some authors concluded that muscle oxidative capacity, rather than cardiovascular oxygen transport, limits
of altitude-acclimatized subjects who are staying in chronic hypoxia, after sudden exposure to normoxic gas mixtures, does not return to the pre-acclimatization levels (Cerretelli 1976). On these bases, some authors concluded that muscle oxidative capacity, rather than cardiovascular oxygen transport, limits 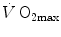 (Cerretelli 1980; Lindstedt et al. 1988; Taylor 1987; Weibel 1987), especially during exercise with small muscle groups (Davies and Sargeant 1974; Kaijser 1970; Saltin 1977). More recently, this view was supported also by experiments with single-leg extension exercise (Rådegran et al. 1999; Richardson et al. 1995b; Roach et al. 1999). With the same experimental model, Calbet et al. (2009) demonstrated also a different
(Cerretelli 1980; Lindstedt et al. 1988; Taylor 1987; Weibel 1987), especially during exercise with small muscle groups (Davies and Sargeant 1974; Kaijser 1970; Saltin 1977). More recently, this view was supported also by experiments with single-leg extension exercise (Rådegran et al. 1999; Richardson et al. 1995b; Roach et al. 1999). With the same experimental model, Calbet et al. (2009) demonstrated also a different 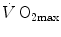 decrease in hypoxia when exercise was performed with small rather than big muscle masses. In a minority of cases, such as extreme hypoxia (West 1983) and in athletes with very high
decrease in hypoxia when exercise was performed with small rather than big muscle masses. In a minority of cases, such as extreme hypoxia (West 1983) and in athletes with very high 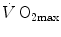 values (Dempsey et al. 1984; Dempsey and Wagner 1999), the lungs were also accounted for as limiting step.
values (Dempsey et al. 1984; Dempsey and Wagner 1999), the lungs were also accounted for as limiting step.
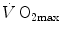 (Åstrand and Saltin 1961; Bergh et al. 1976; Davies and Sargeant 1974; Secher et al. 1974); (ii) specific endurance training of one leg increases
(Åstrand and Saltin 1961; Bergh et al. 1976; Davies and Sargeant 1974; Secher et al. 1974); (ii) specific endurance training of one leg increases 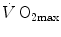 during exercise with that leg only (Saltin et al. 1976); (iii) endurance athletes have a greater fraction of oxidative type I muscle fibres, a greater muscle capillary density and a higher activity of muscle oxidative enzymes than sedentary individuals (Brodal et al. 1977; Costill et al. 1976; Gollnick et al. 1972; Howald 1982; Tesch and Karlsson 1985; Zumstein et al. 1983); (iv) muscle capillary supply, muscle mitochondrial volume and muscle oxidative enzyme activities are increased by physical training (Andersen and Henriksson 1977; Gollnick et al. 1973; Henriksson 1977; Holloszy and Coyle 1984; Hoppeler et al. 1985; Howald et al. 1985; Ingjer 1979) and decreased by prolonged inactivity (Berg et al. 1993; Booth 1982; Hikida et al. 1989). Furthermore, and most importantly, the
during exercise with that leg only (Saltin et al. 1976); (iii) endurance athletes have a greater fraction of oxidative type I muscle fibres, a greater muscle capillary density and a higher activity of muscle oxidative enzymes than sedentary individuals (Brodal et al. 1977; Costill et al. 1976; Gollnick et al. 1972; Howald 1982; Tesch and Karlsson 1985; Zumstein et al. 1983); (iv) muscle capillary supply, muscle mitochondrial volume and muscle oxidative enzyme activities are increased by physical training (Andersen and Henriksson 1977; Gollnick et al. 1973; Henriksson 1977; Holloszy and Coyle 1984; Hoppeler et al. 1985; Howald et al. 1985; Ingjer 1979) and decreased by prolonged inactivity (Berg et al. 1993; Booth 1982; Hikida et al. 1989). Furthermore, and most importantly, the 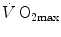 of altitude-acclimatized subjects who are staying in chronic hypoxia, after sudden exposure to normoxic gas mixtures, does not return to the pre-acclimatization levels (Cerretelli 1976). On these bases, some authors concluded that muscle oxidative capacity, rather than cardiovascular oxygen transport, limits
of altitude-acclimatized subjects who are staying in chronic hypoxia, after sudden exposure to normoxic gas mixtures, does not return to the pre-acclimatization levels (Cerretelli 1976). On these bases, some authors concluded that muscle oxidative capacity, rather than cardiovascular oxygen transport, limits 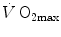 (Cerretelli 1980; Lindstedt et al. 1988; Taylor 1987; Weibel 1987), especially during exercise with small muscle groups (Davies and Sargeant 1974; Kaijser 1970; Saltin 1977). More recently, this view was supported also by experiments with single-leg extension exercise (Rådegran et al. 1999; Richardson et al. 1995b; Roach et al. 1999). With the same experimental model, Calbet et al. (2009) demonstrated also a different
(Cerretelli 1980; Lindstedt et al. 1988; Taylor 1987; Weibel 1987), especially during exercise with small muscle groups (Davies and Sargeant 1974; Kaijser 1970; Saltin 1977). More recently, this view was supported also by experiments with single-leg extension exercise (Rådegran et al. 1999; Richardson et al. 1995b; Roach et al. 1999). With the same experimental model, Calbet et al. (2009) demonstrated also a different 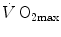 decrease in hypoxia when exercise was performed with small rather than big muscle masses. In a minority of cases, such as extreme hypoxia (West 1983) and in athletes with very high
decrease in hypoxia when exercise was performed with small rather than big muscle masses. In a minority of cases, such as extreme hypoxia (West 1983) and in athletes with very high 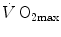 values (Dempsey et al. 1984; Dempsey and Wagner 1999), the lungs were also accounted for as limiting step.
values (Dempsey et al. 1984; Dempsey and Wagner 1999), the lungs were also accounted for as limiting step.The debate on the single factor that limits 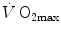 in humans went on for a long time, remaining essentially unresolved. Still in 1992, Saltin and Strange (1992) noted that no consensus existed on what limits
in humans went on for a long time, remaining essentially unresolved. Still in 1992, Saltin and Strange (1992) noted that no consensus existed on what limits 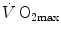 . The concept of a mono-factorial
. The concept of a mono-factorial 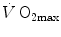 limitation was so deeply rooted in the world of exercise physiology, that even an important recent review on
limitation was so deeply rooted in the world of exercise physiology, that even an important recent review on 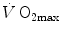 maintained a mono-factorial focus (Levine 2008). However, the revolution generated by the introduction of multifactorial models of
maintained a mono-factorial focus (Levine 2008). However, the revolution generated by the introduction of multifactorial models of 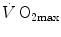 limitation has transformed the inconclusive debate on the cardiovascular versus muscular limitation of
limitation has transformed the inconclusive debate on the cardiovascular versus muscular limitation of 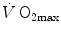 into an old-fashioned reminiscence of the past, similarly to what has happened to tape recorders for experimental data collection.
into an old-fashioned reminiscence of the past, similarly to what has happened to tape recorders for experimental data collection.
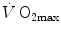 in humans went on for a long time, remaining essentially unresolved. Still in 1992, Saltin and Strange (1992) noted that no consensus existed on what limits
in humans went on for a long time, remaining essentially unresolved. Still in 1992, Saltin and Strange (1992) noted that no consensus existed on what limits 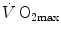 . The concept of a mono-factorial
. The concept of a mono-factorial 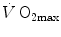 limitation was so deeply rooted in the world of exercise physiology, that even an important recent review on
limitation was so deeply rooted in the world of exercise physiology, that even an important recent review on 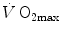 maintained a mono-factorial focus (Levine 2008). However, the revolution generated by the introduction of multifactorial models of
maintained a mono-factorial focus (Levine 2008). However, the revolution generated by the introduction of multifactorial models of 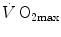 limitation has transformed the inconclusive debate on the cardiovascular versus muscular limitation of
limitation has transformed the inconclusive debate on the cardiovascular versus muscular limitation of 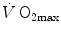 into an old-fashioned reminiscence of the past, similarly to what has happened to tape recorders for experimental data collection.
into an old-fashioned reminiscence of the past, similarly to what has happened to tape recorders for experimental data collection.The Oxygen Cascade at Maximal Exercise
The theory of the oxygen cascade represents an attempt at developing a comprehensive, integrative view of the respiratory system as a gas transporter from ambient air to the mitochondria or vice versa. The basic concept, which can be taken as the axiom behind multifactorial models of 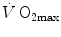 limitation, describes oxygen as flowing along the respiratory system driven by oxygen pressure gradients against several in-series resistances, in analogy with water flow in pipes or current in high-resistance electric lines. The overall driving pressure is the pressure gradient between inspired air and the mitochondria. Oxygen partial pressure can be measured at various levels along the respiratory system: the measured values decrease as long as we proceed from the mouth to the mitochondria. These measurement sites allow definition of clear and physiologically significant resistances to flow. A representation of the oxygen flow from ambient air to the mitochondria is depicted in Fig. 1.3 (see Chap. 1). The set of equations describing the flow of oxygen across each resistance provides a simple quantitative description of the oxygen cascade theory. A more detailed nonlinear algebraic solution of the oxygen conductance equations can be found elsewhere (Shephard 1969). At steady state, all these equations have equal solutions for oxygen flow (see Chap. 1), which, at maximal exercise, corresponds to
limitation, describes oxygen as flowing along the respiratory system driven by oxygen pressure gradients against several in-series resistances, in analogy with water flow in pipes or current in high-resistance electric lines. The overall driving pressure is the pressure gradient between inspired air and the mitochondria. Oxygen partial pressure can be measured at various levels along the respiratory system: the measured values decrease as long as we proceed from the mouth to the mitochondria. These measurement sites allow definition of clear and physiologically significant resistances to flow. A representation of the oxygen flow from ambient air to the mitochondria is depicted in Fig. 1.3 (see Chap. 1). The set of equations describing the flow of oxygen across each resistance provides a simple quantitative description of the oxygen cascade theory. A more detailed nonlinear algebraic solution of the oxygen conductance equations can be found elsewhere (Shephard 1969). At steady state, all these equations have equal solutions for oxygen flow (see Chap. 1), which, at maximal exercise, corresponds to 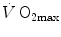 , i.e. the maximal flow of oxygen that the incurring overall pressure gradient can sustain against the total resistance to oxygen flow. This resistance decreases as long as the body metabolism is increased, because of the concomitant elevation of ventilation, diffusion capacity, cardiovascular oxygen flow and muscle blood flow. The resistance at maximal exercise, opposing to
, i.e. the maximal flow of oxygen that the incurring overall pressure gradient can sustain against the total resistance to oxygen flow. This resistance decreases as long as the body metabolism is increased, because of the concomitant elevation of ventilation, diffusion capacity, cardiovascular oxygen flow and muscle blood flow. The resistance at maximal exercise, opposing to 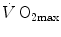 , is the minimal resistance opposed by the respiratory system to oxygen flow.
, is the minimal resistance opposed by the respiratory system to oxygen flow.
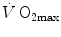 limitation, describes oxygen as flowing along the respiratory system driven by oxygen pressure gradients against several in-series resistances, in analogy with water flow in pipes or current in high-resistance electric lines. The overall driving pressure is the pressure gradient between inspired air and the mitochondria. Oxygen partial pressure can be measured at various levels along the respiratory system: the measured values decrease as long as we proceed from the mouth to the mitochondria. These measurement sites allow definition of clear and physiologically significant resistances to flow. A representation of the oxygen flow from ambient air to the mitochondria is depicted in Fig. 1.3 (see Chap. 1). The set of equations describing the flow of oxygen across each resistance provides a simple quantitative description of the oxygen cascade theory. A more detailed nonlinear algebraic solution of the oxygen conductance equations can be found elsewhere (Shephard 1969). At steady state, all these equations have equal solutions for oxygen flow (see Chap. 1), which, at maximal exercise, corresponds to
limitation, describes oxygen as flowing along the respiratory system driven by oxygen pressure gradients against several in-series resistances, in analogy with water flow in pipes or current in high-resistance electric lines. The overall driving pressure is the pressure gradient between inspired air and the mitochondria. Oxygen partial pressure can be measured at various levels along the respiratory system: the measured values decrease as long as we proceed from the mouth to the mitochondria. These measurement sites allow definition of clear and physiologically significant resistances to flow. A representation of the oxygen flow from ambient air to the mitochondria is depicted in Fig. 1.3 (see Chap. 1). The set of equations describing the flow of oxygen across each resistance provides a simple quantitative description of the oxygen cascade theory. A more detailed nonlinear algebraic solution of the oxygen conductance equations can be found elsewhere (Shephard 1969). At steady state, all these equations have equal solutions for oxygen flow (see Chap. 1), which, at maximal exercise, corresponds to 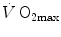 , i.e. the maximal flow of oxygen that the incurring overall pressure gradient can sustain against the total resistance to oxygen flow. This resistance decreases as long as the body metabolism is increased, because of the concomitant elevation of ventilation, diffusion capacity, cardiovascular oxygen flow and muscle blood flow. The resistance at maximal exercise, opposing to
, i.e. the maximal flow of oxygen that the incurring overall pressure gradient can sustain against the total resistance to oxygen flow. This resistance decreases as long as the body metabolism is increased, because of the concomitant elevation of ventilation, diffusion capacity, cardiovascular oxygen flow and muscle blood flow. The resistance at maximal exercise, opposing to 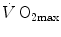 , is the minimal resistance opposed by the respiratory system to oxygen flow.
, is the minimal resistance opposed by the respiratory system to oxygen flow.Two variants of the oxygen cascade theory at maximal exercise have been proposed, depending on whether the cardiovascular oxygen transport step is considered merely convective or not. A convective cardiovascular step implies that the driving force of oxygen flow across this step is the gradient set by the mean capillary oxygen partial pressures (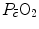 ) in the lungs and in muscles, which can be calculated by Bohr’s integration at the respective capillaries. In this case, the cardiovascular system would be seen as an element connecting two distant resistances, not as a resistive step in se. If conversely cardiovascular oxygen transport is not considered convective, the driving force across it would be the difference between arterial and mixed venous oxygen partial pressures (
) in the lungs and in muscles, which can be calculated by Bohr’s integration at the respective capillaries. In this case, the cardiovascular system would be seen as an element connecting two distant resistances, not as a resistive step in se. If conversely cardiovascular oxygen transport is not considered convective, the driving force across it would be the difference between arterial and mixed venous oxygen partial pressures (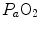 and
and 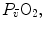 respectively), thus making blood circulation one of the many in-series resistances of a hydraulic system.
respectively), thus making blood circulation one of the many in-series resistances of a hydraulic system.
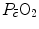 ) in the lungs and in muscles, which can be calculated by Bohr’s integration at the respective capillaries. In this case, the cardiovascular system would be seen as an element connecting two distant resistances, not as a resistive step in se. If conversely cardiovascular oxygen transport is not considered convective, the driving force across it would be the difference between arterial and mixed venous oxygen partial pressures (
) in the lungs and in muscles, which can be calculated by Bohr’s integration at the respective capillaries. In this case, the cardiovascular system would be seen as an element connecting two distant resistances, not as a resistive step in se. If conversely cardiovascular oxygen transport is not considered convective, the driving force across it would be the difference between arterial and mixed venous oxygen partial pressures (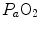 and
and 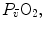 respectively), thus making blood circulation one of the many in-series resistances of a hydraulic system.
respectively), thus making blood circulation one of the many in-series resistances of a hydraulic system.Both interpretations of cardiovascular oxygen transport can be considered viable because there is a still unresolved quantitative step in the oxygen cascade theory: the effects of the heterogeneity of distribution of the ventilation/perfusion ratio (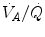 ) in the lungs, which generates the difference between mean alveolar oxygen partial pressure (
) in the lungs, which generates the difference between mean alveolar oxygen partial pressure (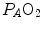 ) and
) and 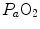 . The best analytical tool conceived for the description of oxygen transfer between alveoli and arterial blood is the diffusion–perfusion interaction equation for the lung (Piiper and Scheid 1981), which nevertheless does not include the effect of
. The best analytical tool conceived for the description of oxygen transfer between alveoli and arterial blood is the diffusion–perfusion interaction equation for the lung (Piiper and Scheid 1981), which nevertheless does not include the effect of 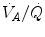 heterogeneity on
heterogeneity on 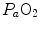 . The genesis of the two above-mentioned interpretations of cardiovascular oxygen transport is a consequence of the manner this unresolved step of the oxygen cascade is treated, and these two interpretations are at the basis of the two main multifactorial models of
. The genesis of the two above-mentioned interpretations of cardiovascular oxygen transport is a consequence of the manner this unresolved step of the oxygen cascade is treated, and these two interpretations are at the basis of the two main multifactorial models of 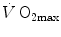 limitation, respectively conceived by Pietro Enrico di Prampero and by Peter Wagner (Fig. 4.2). This generated some apparent conceptual and analytical differences in the respective formulations, which led to consider the two models as conflicting. It was recently demonstrated that this was not the case indeed, at least as long as the analysis is restricted to the trait of the respiratory system distal to arterial blood (Ferretti 2014). This restriction is acceptable in normoxia, as long as it is admitted that there is no limitation of
limitation, respectively conceived by Pietro Enrico di Prampero and by Peter Wagner (Fig. 4.2). This generated some apparent conceptual and analytical differences in the respective formulations, which led to consider the two models as conflicting. It was recently demonstrated that this was not the case indeed, at least as long as the analysis is restricted to the trait of the respiratory system distal to arterial blood (Ferretti 2014). This restriction is acceptable in normoxia, as long as it is admitted that there is no limitation of 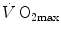 imposed by pulmonary ventilation and lung diffusion in this condition.
imposed by pulmonary ventilation and lung diffusion in this condition.

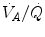 ) in the lungs, which generates the difference between mean alveolar oxygen partial pressure (
) in the lungs, which generates the difference between mean alveolar oxygen partial pressure (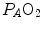 ) and
) and 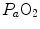 . The best analytical tool conceived for the description of oxygen transfer between alveoli and arterial blood is the diffusion–perfusion interaction equation for the lung (Piiper and Scheid 1981), which nevertheless does not include the effect of
. The best analytical tool conceived for the description of oxygen transfer between alveoli and arterial blood is the diffusion–perfusion interaction equation for the lung (Piiper and Scheid 1981), which nevertheless does not include the effect of 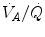 heterogeneity on
heterogeneity on 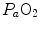 . The genesis of the two above-mentioned interpretations of cardiovascular oxygen transport is a consequence of the manner this unresolved step of the oxygen cascade is treated, and these two interpretations are at the basis of the two main multifactorial models of
. The genesis of the two above-mentioned interpretations of cardiovascular oxygen transport is a consequence of the manner this unresolved step of the oxygen cascade is treated, and these two interpretations are at the basis of the two main multifactorial models of 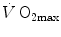 limitation, respectively conceived by Pietro Enrico di Prampero and by Peter Wagner (Fig. 4.2). This generated some apparent conceptual and analytical differences in the respective formulations, which led to consider the two models as conflicting. It was recently demonstrated that this was not the case indeed, at least as long as the analysis is restricted to the trait of the respiratory system distal to arterial blood (Ferretti 2014). This restriction is acceptable in normoxia, as long as it is admitted that there is no limitation of
limitation, respectively conceived by Pietro Enrico di Prampero and by Peter Wagner (Fig. 4.2). This generated some apparent conceptual and analytical differences in the respective formulations, which led to consider the two models as conflicting. It was recently demonstrated that this was not the case indeed, at least as long as the analysis is restricted to the trait of the respiratory system distal to arterial blood (Ferretti 2014). This restriction is acceptable in normoxia, as long as it is admitted that there is no limitation of 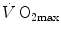 imposed by pulmonary ventilation and lung diffusion in this condition.
imposed by pulmonary ventilation and lung diffusion in this condition.
Fig. 4.2
From left to right, Peter Wagner, Fabio Benfenati (then President of the Italian Physiological Society), Arsenio Veicsteinas, Pietro Enrico di Prampero, Guido Ferretti, Fabio Esposito, Carlo Capelli and Paolo Cerretelli. Wagner and di Prampero are the creators of the two multifactorial models of  limitation. Picture taken at the 62° annual meeting of the Italian Physiological Society, which took place in Sorrento, Italy, on 25–27 September 2011. Courtesy of Arsenio Veicsteinas
limitation. Picture taken at the 62° annual meeting of the Italian Physiological Society, which took place in Sorrento, Italy, on 25–27 September 2011. Courtesy of Arsenio Veicsteinas
 limitation. Picture taken at the 62° annual meeting of the Italian Physiological Society, which took place in Sorrento, Italy, on 25–27 September 2011. Courtesy of Arsenio Veicsteinas
limitation. Picture taken at the 62° annual meeting of the Italian Physiological Society, which took place in Sorrento, Italy, on 25–27 September 2011. Courtesy of Arsenio VeicsteinasAn Analysis of di Prampero’s Model
di Prampero’s model (di Prampero 1985, 2003; di Prampero and Ferretti 1990; Ferretti and di Prampero 1995) looks at the respiratory system from ambient air to the mitochondria as a hydraulic model of in-series resistances and assumes steady-state condition at maximal exercise. If this is so, for a system characterized by n resistances in series, we have:
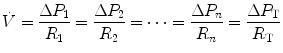
where 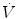 is the gas flow, ΔP is the pressure gradient sustaining
is the gas flow, ΔP is the pressure gradient sustaining 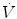 across the ith resistance R and
across the ith resistance R and 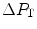 is the overall pressure gradient. At maximal exercise,
is the overall pressure gradient. At maximal exercise, 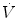 is
is 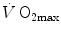 and
and 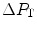 is the difference between the inspired and the mitochondrial partial pressure of oxygen,
is the difference between the inspired and the mitochondrial partial pressure of oxygen, 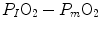 . Since
. Since 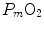 tends to 0 mmHg (Gayeski and Honig 1986; Richardson et al. 2001; Wagner 2012),
tends to 0 mmHg (Gayeski and Honig 1986; Richardson et al. 2001; Wagner 2012), 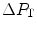 can be set equal to
can be set equal to 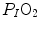 with negligible error. Of course, ΔPT is the sum of the pressure gradients across each resistance:
with negligible error. Of course, ΔPT is the sum of the pressure gradients across each resistance:
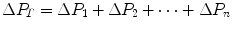
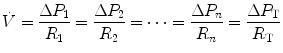
(4.1)
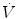 is the gas flow, ΔP is the pressure gradient sustaining
is the gas flow, ΔP is the pressure gradient sustaining 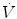 across the ith resistance R and
across the ith resistance R and 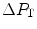 is the overall pressure gradient. At maximal exercise,
is the overall pressure gradient. At maximal exercise, 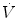 is
is 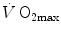 and
and 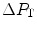 is the difference between the inspired and the mitochondrial partial pressure of oxygen,
is the difference between the inspired and the mitochondrial partial pressure of oxygen, 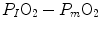 . Since
. Since 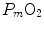 tends to 0 mmHg (Gayeski and Honig 1986; Richardson et al. 2001; Wagner 2012),
tends to 0 mmHg (Gayeski and Honig 1986; Richardson et al. 2001; Wagner 2012), 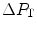 can be set equal to
can be set equal to 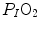 with negligible error. Of course, ΔPT is the sum of the pressure gradients across each resistance:
with negligible error. Of course, ΔPT is the sum of the pressure gradients across each resistance: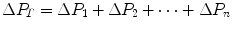
(4.2)
In this case, the fraction of the overall limitation imposed by the ith resistance to oxygen flow is given by:
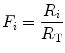
whence
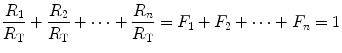
indicating that the overall limitation to oxygen flow in this model is equal to the sum of the fractional limitations imposed by each of the resistances in the system.
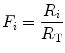
(4.3)
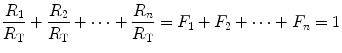
(4.4)
The portrait of the oxygen cascade presented in Fig. 1.3 allows identification of five resistances of clear physiological meaning, namely from proximal (ambient air) to distal (mitochondria), (i) the ventilatory resistance (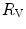 ), (ii) the lung resistance (
), (ii) the lung resistance (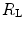 ), which refers to the transfer of oxygen from the alveoli to the arterial blood, (iii) the cardiovascular resistance (
), which refers to the transfer of oxygen from the alveoli to the arterial blood, (iii) the cardiovascular resistance (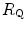 ), (iv) the tissue resistance (
), (iv) the tissue resistance (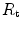 ), which refers to oxygen transfer from peripheral capillaries to muscle fibres and (v) the mitochondrial resistance (
), which refers to oxygen transfer from peripheral capillaries to muscle fibres and (v) the mitochondrial resistance (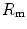 ), related to mitochondrial oxygen flow and utilization. Although these resistances are related to general concepts that can easily be perceived, discrimination between
), related to mitochondrial oxygen flow and utilization. Although these resistances are related to general concepts that can easily be perceived, discrimination between 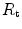 and
and 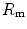 is virtually impossible, because they are strongly interrelated on a structural basis. Therefore, for subsequent analysis, they are merged to form a lumped peripheral resistance (
is virtually impossible, because they are strongly interrelated on a structural basis. Therefore, for subsequent analysis, they are merged to form a lumped peripheral resistance (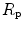 ). For the specific case of
). For the specific case of 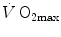 , Eq. (4.1) can thus be rewritten as follows:
, Eq. (4.1) can thus be rewritten as follows:
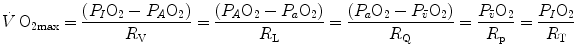
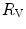 ), (ii) the lung resistance (
), (ii) the lung resistance (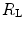 ), which refers to the transfer of oxygen from the alveoli to the arterial blood, (iii) the cardiovascular resistance (
), which refers to the transfer of oxygen from the alveoli to the arterial blood, (iii) the cardiovascular resistance (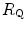 ), (iv) the tissue resistance (
), (iv) the tissue resistance (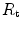 ), which refers to oxygen transfer from peripheral capillaries to muscle fibres and (v) the mitochondrial resistance (
), which refers to oxygen transfer from peripheral capillaries to muscle fibres and (v) the mitochondrial resistance (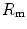 ), related to mitochondrial oxygen flow and utilization. Although these resistances are related to general concepts that can easily be perceived, discrimination between
), related to mitochondrial oxygen flow and utilization. Although these resistances are related to general concepts that can easily be perceived, discrimination between 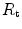 and
and 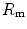 is virtually impossible, because they are strongly interrelated on a structural basis. Therefore, for subsequent analysis, they are merged to form a lumped peripheral resistance (
is virtually impossible, because they are strongly interrelated on a structural basis. Therefore, for subsequent analysis, they are merged to form a lumped peripheral resistance (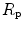 ). For the specific case of
). For the specific case of 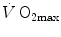 , Eq. (4.1) can thus be rewritten as follows:
, Eq. (4.1) can thus be rewritten as follows: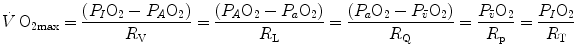
(4.5)
Of these resistances, only two are characterized by precisely defined physiological variables, namely 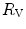 and
and 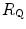 , which are, respectively, equal to:
, which are, respectively, equal to:
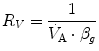
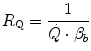
where 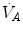 is alveolar ventilation and
is alveolar ventilation and 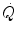 is cardiac output. The other two variables are the oxygen transfer coefficient for air (
is cardiac output. The other two variables are the oxygen transfer coefficient for air (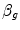 ) and for blood (
) and for blood (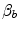 ), i.e. the volume of oxygen that can be displaced across a gradient of a unit of pressure. In STPD condition,
), i.e. the volume of oxygen that can be displaced across a gradient of a unit of pressure. In STPD condition, 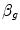 is equal to 1.16 ml mmHg−1 and is an invariant constant. Concerning
is equal to 1.16 ml mmHg−1 and is an invariant constant. Concerning 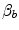 , it is equal to:
, it is equal to:
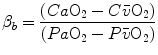
that is the average slope of the oxygen equilibrium curve. Therefore, constant 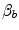 is not an invariant value, for it depends on the oxygen pressure range on which blood operates. The other three resistances cannot be translated into equivalent physiological expressions.
is not an invariant value, for it depends on the oxygen pressure range on which blood operates. The other three resistances cannot be translated into equivalent physiological expressions. 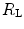 ,
, 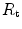 and
and 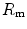 were set proportional, respectively, to a factor including lung diffusing capacity corrected for the effect of
were set proportional, respectively, to a factor including lung diffusing capacity corrected for the effect of 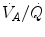 heterogeneity, to muscle capillary density and to muscle mitochondrial volume (di Prampero and Ferretti 1990).
heterogeneity, to muscle capillary density and to muscle mitochondrial volume (di Prampero and Ferretti 1990).
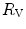 and
and 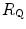 , which are, respectively, equal to:
, which are, respectively, equal to: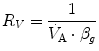
(4.6a)
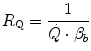
(4.6b)
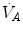 is alveolar ventilation and
is alveolar ventilation and 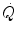 is cardiac output. The other two variables are the oxygen transfer coefficient for air (
is cardiac output. The other two variables are the oxygen transfer coefficient for air (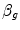 ) and for blood (
) and for blood (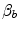 ), i.e. the volume of oxygen that can be displaced across a gradient of a unit of pressure. In STPD condition,
), i.e. the volume of oxygen that can be displaced across a gradient of a unit of pressure. In STPD condition, 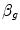 is equal to 1.16 ml mmHg−1 and is an invariant constant. Concerning
is equal to 1.16 ml mmHg−1 and is an invariant constant. Concerning 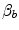 , it is equal to:
, it is equal to: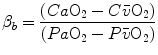
(4.7)
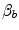 is not an invariant value, for it depends on the oxygen pressure range on which blood operates. The other three resistances cannot be translated into equivalent physiological expressions.
is not an invariant value, for it depends on the oxygen pressure range on which blood operates. The other three resistances cannot be translated into equivalent physiological expressions. 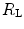 ,
, 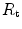 and
and 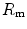 were set proportional, respectively, to a factor including lung diffusing capacity corrected for the effect of
were set proportional, respectively, to a factor including lung diffusing capacity corrected for the effect of 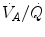 heterogeneity, to muscle capillary density and to muscle mitochondrial volume (di Prampero and Ferretti 1990).
heterogeneity, to muscle capillary density and to muscle mitochondrial volume (di Prampero and Ferretti 1990).When a manipulation, either chronic or acute, affects 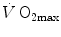 without affecting
without affecting 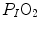 , and thus ΔP T, the observed increase in
, and thus ΔP T, the observed increase in 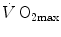 is the result of changes in one or more of the resistances in series. Thus, the model was devised in such a manner as to provide a value for the fraction of the overall
is the result of changes in one or more of the resistances in series. Thus, the model was devised in such a manner as to provide a value for the fraction of the overall 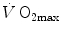 limitation which any given in-series resistance is responsible for. For instance, aerobic training provides a given
limitation which any given in-series resistance is responsible for. For instance, aerobic training provides a given 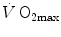 increase,
increase, 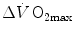 , because some resistances (at least three in this case, namely
, because some resistances (at least three in this case, namely 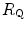 ,
, 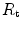 and
and 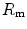 ) have decreased, and so has
) have decreased, and so has 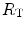 . Thus, after training has induced a measurable increase in
. Thus, after training has induced a measurable increase in 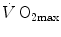 with respect to the value before training, Eq. (4.5) can be rewritten as follows:
with respect to the value before training, Eq. (4.5) can be rewritten as follows:
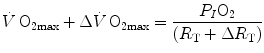
If we divide Eq. (4.5) by Eq. (4.8), we get:
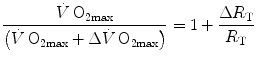
which, since 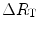 is the sum of the changes in the ith resistances in series, it can also take the following form:
is the sum of the changes in the ith resistances in series, it can also take the following form:
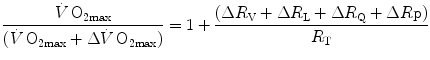
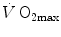 without affecting
without affecting 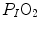 , and thus ΔP T, the observed increase in
, and thus ΔP T, the observed increase in 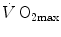 is the result of changes in one or more of the resistances in series. Thus, the model was devised in such a manner as to provide a value for the fraction of the overall
is the result of changes in one or more of the resistances in series. Thus, the model was devised in such a manner as to provide a value for the fraction of the overall 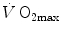 limitation which any given in-series resistance is responsible for. For instance, aerobic training provides a given
limitation which any given in-series resistance is responsible for. For instance, aerobic training provides a given 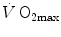 increase,
increase, 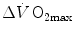 , because some resistances (at least three in this case, namely
, because some resistances (at least three in this case, namely 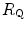 ,
, 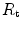 and
and 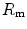 ) have decreased, and so has
) have decreased, and so has 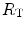 . Thus, after training has induced a measurable increase in
. Thus, after training has induced a measurable increase in 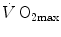 with respect to the value before training, Eq. (4.5) can be rewritten as follows:
with respect to the value before training, Eq. (4.5) can be rewritten as follows: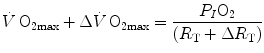
(4.8)
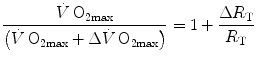
(4.9)
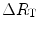 is the sum of the changes in the ith resistances in series, it can also take the following form:
is the sum of the changes in the ith resistances in series, it can also take the following form: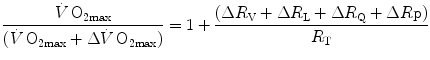
(4.10)
As a consequence of Eqs. (4.3) and (4.4), the induction of a change in any resistance by a manoeuvre specifically acting on it yields:
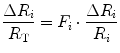
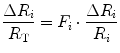
(4.11)
Equation (4.12) has four unknowns and as such cannot be solved. However, if we take a condition wherein only one resistance is varied by an acute manipulation, as is the case, according to di Prampero and Ferretti (1990), for 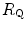 after acute blood reinfusion or withdrawal, three terms of Eq. (4.12) annihilate. Thus, we remain with a simplified version of it, with only one unknown. For the specific case of changes in
after acute blood reinfusion or withdrawal, three terms of Eq. (4.12) annihilate. Thus, we remain with a simplified version of it, with only one unknown. For the specific case of changes in 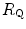 only, Eq. (4.12) takes therefore the following form:
only, Eq. (4.12) takes therefore the following form:
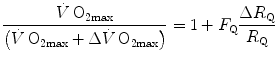
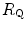 after acute blood reinfusion or withdrawal, three terms of Eq. (4.12) annihilate. Thus, we remain with a simplified version of it, with only one unknown. For the specific case of changes in
after acute blood reinfusion or withdrawal, three terms of Eq. (4.12) annihilate. Thus, we remain with a simplified version of it, with only one unknown. For the specific case of changes in 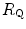 only, Eq. (4.12) takes therefore the following form:
only, Eq. (4.12) takes therefore the following form: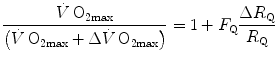
(4.13)
Equation (4.13) allows computation of 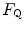 , provided we know the
, provided we know the 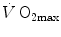 before and after the manoeuvre, the
before and after the manoeuvre, the 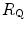 before the manoeuvre and the absolute change in
before the manoeuvre and the absolute change in 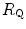 induced by the manoeuvre. An analytical solution of Eq. (4.13), using data from different sources in the literature, is reported in Fig. 4.3, where the ratio between the
induced by the manoeuvre. An analytical solution of Eq. (4.13), using data from different sources in the literature, is reported in Fig. 4.3, where the ratio between the 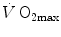 values before and after the manoeuvre (left-hand branch of Eq. 4.13) is plotted as a function of the ratio between
values before and after the manoeuvre (left-hand branch of Eq. 4.13) is plotted as a function of the ratio between 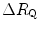 and
and 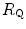 . Equation (4.13) tells that this relationship is linear, with y-intercept equal to 1 and slope equal to
. Equation (4.13) tells that this relationship is linear, with y-intercept equal to 1 and slope equal to 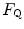 . From linear regression analysis of the data shown in Fig. 4.3, di Prampero and Ferretti (1990) obtained
. From linear regression analysis of the data shown in Fig. 4.3, di Prampero and Ferretti (1990) obtained 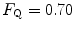 . This means that
. This means that 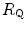 provides 70 % of the fractional limitation of
provides 70 % of the fractional limitation of 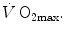
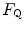 , provided we know the
, provided we know the 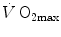 before and after the manoeuvre, the
before and after the manoeuvre, the 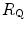 before the manoeuvre and the absolute change in
before the manoeuvre and the absolute change in 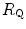 induced by the manoeuvre. An analytical solution of Eq. (4.13), using data from different sources in the literature, is reported in Fig. 4.3, where the ratio between the
induced by the manoeuvre. An analytical solution of Eq. (4.13), using data from different sources in the literature, is reported in Fig. 4.3, where the ratio between the 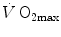 values before and after the manoeuvre (left-hand branch of Eq. 4.13) is plotted as a function of the ratio between
values before and after the manoeuvre (left-hand branch of Eq. 4.13) is plotted as a function of the ratio between 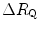 and
and 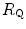 . Equation (4.13) tells that this relationship is linear, with y-intercept equal to 1 and slope equal to
. Equation (4.13) tells that this relationship is linear, with y-intercept equal to 1 and slope equal to 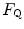 . From linear regression analysis of the data shown in Fig. 4.3, di Prampero and Ferretti (1990) obtained
. From linear regression analysis of the data shown in Fig. 4.3, di Prampero and Ferretti (1990) obtained 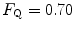 . This means that
. This means that 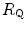 provides 70 % of the fractional limitation of
provides 70 % of the fractional limitation of 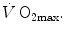
An 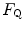 value equal to 0.70 implies that the respiratory system does not have linear behaviour. In fact, for a linear respiratory system, the ratio of any given
value equal to 0.70 implies that the respiratory system does not have linear behaviour. In fact, for a linear respiratory system, the ratio of any given 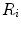 to
to 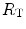 would be equal to the ratio of the pressure gradient over that
would be equal to the ratio of the pressure gradient over that 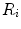 to the overall pressure gradient, so that:
to the overall pressure gradient, so that:
from which we would have obtained 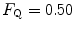 instead of 0.70 (di Prampero and Ferretti 1990). The source of nonlinearity, and thus the source of this discrepancy, was identified in the effects of the oxygen equilibrium curve on
instead of 0.70 (di Prampero and Ferretti 1990). The source of nonlinearity, and thus the source of this discrepancy, was identified in the effects of the oxygen equilibrium curve on 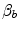 , as shown in Fig. 4.4. Assume that an acute manoeuvre acts directly on
, as shown in Fig. 4.4. Assume that an acute manoeuvre acts directly on 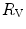 only, e.g. reducing it. This would increase
only, e.g. reducing it. This would increase 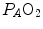 , and thus
, and thus 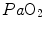 , but would not change the associated
, but would not change the associated 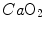 , because in normoxia our blood operates on the flat portion of the oxygen equilibrium curve. Therefore, since
, because in normoxia our blood operates on the flat portion of the oxygen equilibrium curve. Therefore, since 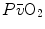 undergoes only small changes,
undergoes only small changes, 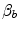 would be reduced, and thus
would be reduced, and thus 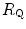 would be increased. In sum, because of the shape of the oxygen equilibrium curve, as long as we are in normoxia, a specific manoeuvre acting only on
would be increased. In sum, because of the shape of the oxygen equilibrium curve, as long as we are in normoxia, a specific manoeuvre acting only on 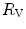 cannot have effects on
cannot have effects on 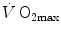 , because any change in
, because any change in 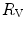 would be counteracted by an opposite change in
would be counteracted by an opposite change in 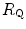 : in normoxia,
: in normoxia, 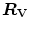 and
and 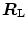 do not limit
do not limit 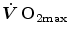 . Using a different terminology, this is the case when perfusion limitation characterises the alveolar-capillary gas transfer. Thus, the effects of the respiratory system on
. Using a different terminology, this is the case when perfusion limitation characterises the alveolar-capillary gas transfer. Thus, the effects of the respiratory system on 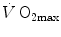 can be fully described by a two-site model wherein the effective limitation is located distally to
can be fully described by a two-site model wherein the effective limitation is located distally to 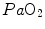 . This explains why
. This explains why 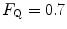 instead of 0.5, so that we necessarily have
instead of 0.5, so that we necessarily have 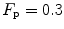 , partly attributable to
, partly attributable to 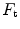 , partly to
, partly to 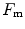 . According to Ferretti et al. (1997a), the differences in
. According to Ferretti et al. (1997a), the differences in 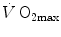 would be minimal, if we assume, on one extreme,
would be minimal, if we assume, on one extreme, 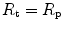 , and on the other extreme,
, and on the other extreme, 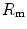 =
= 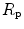 , and that it makes no difference to assume
, and that it makes no difference to assume 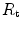 and
and 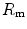 in series or in parallel. Direct experimental assessment of the parameters of Eq. (4.13) confirmed that
in series or in parallel. Direct experimental assessment of the parameters of Eq. (4.13) confirmed that 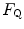 in normoxia is between 0.65 and 0.76 (Bringard et al. 2010; Turner et al. 1993).
in normoxia is between 0.65 and 0.76 (Bringard et al. 2010; Turner et al. 1993).
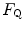 value equal to 0.70 implies that the respiratory system does not have linear behaviour. In fact, for a linear respiratory system, the ratio of any given
value equal to 0.70 implies that the respiratory system does not have linear behaviour. In fact, for a linear respiratory system, the ratio of any given 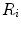 to
to 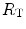 would be equal to the ratio of the pressure gradient over that
would be equal to the ratio of the pressure gradient over that 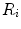 to the overall pressure gradient, so that:
to the overall pressure gradient, so that:
(4.14)
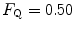 instead of 0.70 (di Prampero and Ferretti 1990). The source of nonlinearity, and thus the source of this discrepancy, was identified in the effects of the oxygen equilibrium curve on
instead of 0.70 (di Prampero and Ferretti 1990). The source of nonlinearity, and thus the source of this discrepancy, was identified in the effects of the oxygen equilibrium curve on 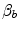 , as shown in Fig. 4.4. Assume that an acute manoeuvre acts directly on
, as shown in Fig. 4.4. Assume that an acute manoeuvre acts directly on 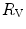 only, e.g. reducing it. This would increase
only, e.g. reducing it. This would increase 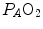 , and thus
, and thus 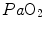 , but would not change the associated
, but would not change the associated 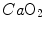 , because in normoxia our blood operates on the flat portion of the oxygen equilibrium curve. Therefore, since
, because in normoxia our blood operates on the flat portion of the oxygen equilibrium curve. Therefore, since 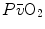 undergoes only small changes,
undergoes only small changes, 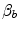 would be reduced, and thus
would be reduced, and thus 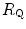 would be increased. In sum, because of the shape of the oxygen equilibrium curve, as long as we are in normoxia, a specific manoeuvre acting only on
would be increased. In sum, because of the shape of the oxygen equilibrium curve, as long as we are in normoxia, a specific manoeuvre acting only on 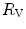 cannot have effects on
cannot have effects on 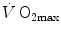 , because any change in
, because any change in 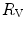 would be counteracted by an opposite change in
would be counteracted by an opposite change in 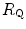 : in normoxia,
: in normoxia, 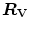 and
and 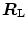 do not limit
do not limit 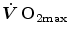 . Using a different terminology, this is the case when perfusion limitation characterises the alveolar-capillary gas transfer. Thus, the effects of the respiratory system on
. Using a different terminology, this is the case when perfusion limitation characterises the alveolar-capillary gas transfer. Thus, the effects of the respiratory system on 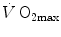 can be fully described by a two-site model wherein the effective limitation is located distally to
can be fully described by a two-site model wherein the effective limitation is located distally to 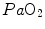 . This explains why
. This explains why 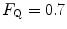 instead of 0.5, so that we necessarily have
instead of 0.5, so that we necessarily have 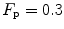 , partly attributable to
, partly attributable to 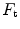 , partly to
, partly to 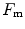 . According to Ferretti et al. (1997a), the differences in
. According to Ferretti et al. (1997a), the differences in 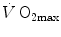 would be minimal, if we assume, on one extreme,
would be minimal, if we assume, on one extreme, 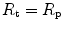 , and on the other extreme,
, and on the other extreme, 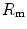 =
= 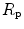 , and that it makes no difference to assume
, and that it makes no difference to assume 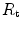 and
and 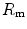 in series or in parallel. Direct experimental assessment of the parameters of Eq. (4.13) confirmed that
in series or in parallel. Direct experimental assessment of the parameters of Eq. (4.13) confirmed that 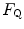 in normoxia is between 0.65 and 0.76 (Bringard et al. 2010; Turner et al. 1993).
in normoxia is between 0.65 and 0.76 (Bringard et al. 2010; Turner et al. 1993).
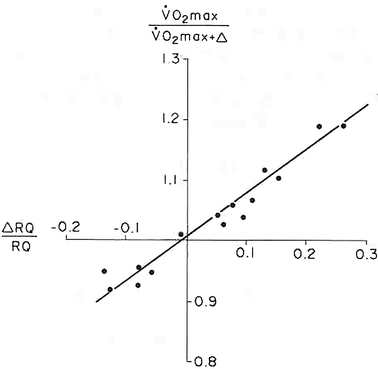
Fig. 4.3
Graphical representation of Eq. (4.13). The changes in 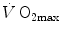 that follow an acute manoeuvre acting on the cardiovascular resistance to oxygen flow (Rq) are expressed as the ratio of the
that follow an acute manoeuvre acting on the cardiovascular resistance to oxygen flow (Rq) are expressed as the ratio of the 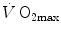 before to the
before to the 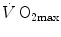 after the manoeuvre at stake (
after the manoeuvre at stake (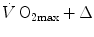 ). This ratio is plotted as a function of the ratio between the induced change in
). This ratio is plotted as a function of the ratio between the induced change in 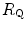 (
(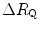 ) and the
) and the 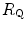 before the manoeuvre. Points are mean values from different sources in the literature. The continuous straight line is the corresponding regression equation (y = 1.006 + 0.7 x, r = 0.97, n = 15). The slope of the line, equal to 0.7, indicates that 70 % of the overall limitation to
before the manoeuvre. Points are mean values from different sources in the literature. The continuous straight line is the corresponding regression equation (y = 1.006 + 0.7 x, r = 0.97, n = 15). The slope of the line, equal to 0.7, indicates that 70 % of the overall limitation to 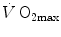 is imposed by cardiovascular oxygen transport. Modified after di Prampero and Ferretti (1990)
is imposed by cardiovascular oxygen transport. Modified after di Prampero and Ferretti (1990)
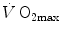 that follow an acute manoeuvre acting on the cardiovascular resistance to oxygen flow (Rq) are expressed as the ratio of the
that follow an acute manoeuvre acting on the cardiovascular resistance to oxygen flow (Rq) are expressed as the ratio of the 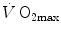 before to the
before to the 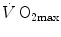 after the manoeuvre at stake (
after the manoeuvre at stake (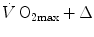 ). This ratio is plotted as a function of the ratio between the induced change in
). This ratio is plotted as a function of the ratio between the induced change in 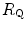 (
(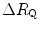 ) and the
) and the 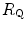 before the manoeuvre. Points are mean values from different sources in the literature. The continuous straight line is the corresponding regression equation (y = 1.006 + 0.7 x, r = 0.97, n = 15). The slope of the line, equal to 0.7, indicates that 70 % of the overall limitation to
before the manoeuvre. Points are mean values from different sources in the literature. The continuous straight line is the corresponding regression equation (y = 1.006 + 0.7 x, r = 0.97, n = 15). The slope of the line, equal to 0.7, indicates that 70 % of the overall limitation to 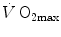 is imposed by cardiovascular oxygen transport. Modified after di Prampero and Ferretti (1990)
is imposed by cardiovascular oxygen transport. Modified after di Prampero and Ferretti (1990)
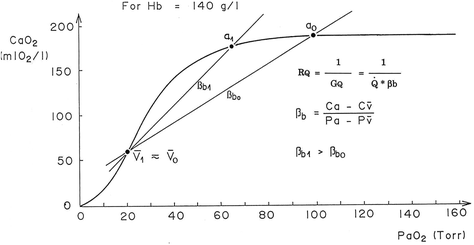
Fig. 4.4
Average oxygen equilibrium curve. Two arterial and mixed venous points are reported, applying to normaemia (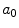 ,
, 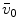 ) and hypoxaemia (
) and hypoxaemia (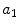 ,
, 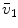 ). The two straight lines connecting the two couples of points have a slope equal to the respective oxygen transport coefficients for blood (
). The two straight lines connecting the two couples of points have a slope equal to the respective oxygen transport coefficients for blood (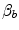 ), which is higher in hypoxaemia than in normaemia. As a consequence, when an increase in the ventilatory resistance
), which is higher in hypoxaemia than in normaemia. As a consequence, when an increase in the ventilatory resistance 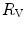 entails a decrease in arterial oxygen partial pressure,
entails a decrease in arterial oxygen partial pressure, 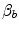 becomes higher and the cardiovascular resistance
becomes higher and the cardiovascular resistance 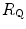 lower. These two phenomena compensate each other, so that no changes in
lower. These two phenomena compensate each other, so that no changes in 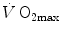 are induced by an acute change in
are induced by an acute change in 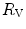 : the lungs do not limit
: the lungs do not limit 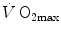 in normoxia. Modified after di Prampero (1985)
in normoxia. Modified after di Prampero (1985)
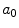 ,
, 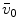 ) and hypoxaemia (
) and hypoxaemia (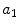 ,
, 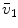 ). The two straight lines connecting the two couples of points have a slope equal to the respective oxygen transport coefficients for blood (
). The two straight lines connecting the two couples of points have a slope equal to the respective oxygen transport coefficients for blood (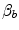 ), which is higher in hypoxaemia than in normaemia. As a consequence, when an increase in the ventilatory resistance
), which is higher in hypoxaemia than in normaemia. As a consequence, when an increase in the ventilatory resistance 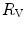 entails a decrease in arterial oxygen partial pressure,
entails a decrease in arterial oxygen partial pressure, 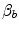 becomes higher and the cardiovascular resistance
becomes higher and the cardiovascular resistance 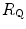 lower. These two phenomena compensate each other, so that no changes in
lower. These two phenomena compensate each other, so that no changes in 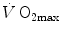 are induced by an acute change in
are induced by an acute change in 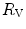 : the lungs do not limit
: the lungs do not limit 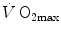 in normoxia. Modified after di Prampero (1985)
in normoxia. Modified after di Prampero (1985)Experimental Testing of di Prampero’s Model
The nonlinear behaviour of the respiratory system implies that within the context of di Prampero’s model (i) 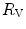 and
and 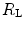 do limit
do limit 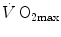 in hypoxia; (ii)
in hypoxia; (ii) 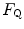 in hypoxia is less than 0.7; (iii) the decrease of
in hypoxia is less than 0.7; (iii) the decrease of 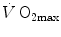 in hypoxia is larger in subjects with high
in hypoxia is larger in subjects with high 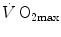 in normoxia; (iv) only subjects with high
in normoxia; (iv) only subjects with high 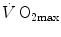 in normoxia undergo an increase in
in normoxia undergo an increase in 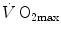 in hyperoxia; (v) exercise with small muscle masses reduces
in hyperoxia; (v) exercise with small muscle masses reduces 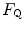 and increases
and increases 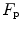 ; (vi) the fall of
; (vi) the fall of 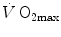 in hypoxia is smaller, the smaller is the contracting muscle mass. Moreover, since the cause of the nonlinear behaviour of the respiratory system is related to the shape of the oxygen equilibrium curve, there must be a linear relationship between
in hypoxia is smaller, the smaller is the contracting muscle mass. Moreover, since the cause of the nonlinear behaviour of the respiratory system is related to the shape of the oxygen equilibrium curve, there must be a linear relationship between 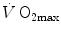 and SaO2.
and SaO2.
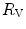 and
and 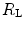 do limit
do limit 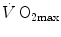 in hypoxia; (ii)
in hypoxia; (ii) 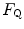 in hypoxia is less than 0.7; (iii) the decrease of
in hypoxia is less than 0.7; (iii) the decrease of 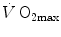 in hypoxia is larger in subjects with high
in hypoxia is larger in subjects with high 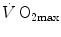 in normoxia; (iv) only subjects with high
in normoxia; (iv) only subjects with high 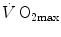 in normoxia undergo an increase in
in normoxia undergo an increase in 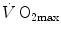 in hyperoxia; (v) exercise with small muscle masses reduces
in hyperoxia; (v) exercise with small muscle masses reduces 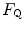 and increases
and increases 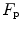 ; (vi) the fall of
; (vi) the fall of 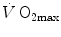 in hypoxia is smaller, the smaller is the contracting muscle mass. Moreover, since the cause of the nonlinear behaviour of the respiratory system is related to the shape of the oxygen equilibrium curve, there must be a linear relationship between
in hypoxia is smaller, the smaller is the contracting muscle mass. Moreover, since the cause of the nonlinear behaviour of the respiratory system is related to the shape of the oxygen equilibrium curve, there must be a linear relationship between 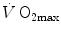 and SaO2.
and SaO2.To investigate the roles played by 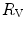 and
and 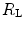 in normoxia and hypoxia, Esposito and Ferretti (1997) changed the air density of the inspired gas mixture by replacing nitrogen with helium, thus reducing
in normoxia and hypoxia, Esposito and Ferretti (1997) changed the air density of the inspired gas mixture by replacing nitrogen with helium, thus reducing 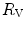 . Although
. Although 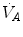 increased in both cases,
increased in both cases, 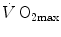 did not change when breathing the He–O2 mixture in normoxia, going up only in hypoxia. Similar results were recently obtained also by Ogawa et al. (2010). Consistently, no effects of respiratory muscle training were shown on
did not change when breathing the He–O2 mixture in normoxia, going up only in hypoxia. Similar results were recently obtained also by Ogawa et al. (2010). Consistently, no effects of respiratory muscle training were shown on 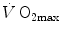 in normoxia, but a positive effect was observed in hypoxia (Downey et al. 2007; Esposito et al. 2010).
in normoxia, but a positive effect was observed in hypoxia (Downey et al. 2007; Esposito et al. 2010).
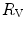 and
and 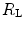 in normoxia and hypoxia, Esposito and Ferretti (1997) changed the air density of the inspired gas mixture by replacing nitrogen with helium, thus reducing
in normoxia and hypoxia, Esposito and Ferretti (1997) changed the air density of the inspired gas mixture by replacing nitrogen with helium, thus reducing 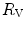 . Although
. Although 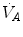 increased in both cases,
increased in both cases, 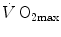 did not change when breathing the He–O2 mixture in normoxia, going up only in hypoxia. Similar results were recently obtained also by Ogawa et al. (2010). Consistently, no effects of respiratory muscle training were shown on
did not change when breathing the He–O2 mixture in normoxia, going up only in hypoxia. Similar results were recently obtained also by Ogawa et al. (2010). Consistently, no effects of respiratory muscle training were shown on 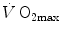 in normoxia, but a positive effect was observed in hypoxia (Downey et al. 2007; Esposito et al. 2010).
in normoxia, but a positive effect was observed in hypoxia (Downey et al. 2007; Esposito et al. 2010).On two groups of subjects, one with high, the other with low 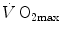 in normoxia, Ferretti et al. (1997b) found that, in the former with respect to the latter group, (i) the decrease in
in normoxia, Ferretti et al. (1997b) found that, in the former with respect to the latter group, (i) the decrease in 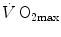 in hypoxia was larger, and (ii) a significant increase in
in hypoxia was larger, and (ii) a significant increase in 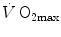 in hyperoxia occurred. Moreover, they found a highly significant linear relationship between
in hyperoxia occurred. Moreover, they found a highly significant linear relationship between 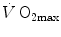 , expressed relative to the value in hyperoxia set equal to 100 %, and SaO2, which was identical in both groups, in agreement with the above predictions. According to Wehrlin and Hallén (2006), the
, expressed relative to the value in hyperoxia set equal to 100 %, and SaO2, which was identical in both groups, in agreement with the above predictions. According to Wehrlin and Hallén (2006), the 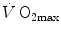 of endurance athletes is so high that the decrease of
of endurance athletes is so high that the decrease of 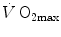 in hypoxia becomes linear. Coherent with this picture is also the finding that the
in hypoxia becomes linear. Coherent with this picture is also the finding that the 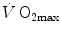 decrease in hypoxia is smaller the stronger is the ventilatory response to hypoxia (Benoit et al. 1995; Gavin et al. 1998; Kayser et al. 1994; Marconi et al. 2004).
decrease in hypoxia is smaller the stronger is the ventilatory response to hypoxia (Benoit et al. 1995; Gavin et al. 1998; Kayser et al. 1994; Marconi et al. 2004).
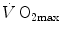 in normoxia, Ferretti et al. (1997b) found that, in the former with respect to the latter group, (i) the decrease in
in normoxia, Ferretti et al. (1997b) found that, in the former with respect to the latter group, (i) the decrease in 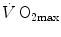 in hypoxia was larger, and (ii) a significant increase in
in hypoxia was larger, and (ii) a significant increase in 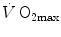 in hyperoxia occurred. Moreover, they found a highly significant linear relationship between
in hyperoxia occurred. Moreover, they found a highly significant linear relationship between 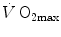 , expressed relative to the value in hyperoxia set equal to 100 %, and SaO2, which was identical in both groups, in agreement with the above predictions. According to Wehrlin and Hallén (2006), the
, expressed relative to the value in hyperoxia set equal to 100 %, and SaO2, which was identical in both groups, in agreement with the above predictions. According to Wehrlin and Hallén (2006), the 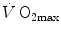 of endurance athletes is so high that the decrease of
of endurance athletes is so high that the decrease of 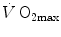 in hypoxia becomes linear. Coherent with this picture is also the finding that the
in hypoxia becomes linear. Coherent with this picture is also the finding that the 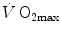 decrease in hypoxia is smaller the stronger is the ventilatory response to hypoxia (Benoit et al. 1995; Gavin et al. 1998; Kayser et al. 1994; Marconi et al. 2004).
decrease in hypoxia is smaller the stronger is the ventilatory response to hypoxia (Benoit et al. 1995; Gavin et al. 1998; Kayser et al. 1994; Marconi et al. 2004).An Analysis of Wagner’s Model
Peter Wagner (1993) constructed a three-equation system with three unknowns (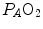 ,
, 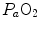 and
and 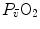 ) by combining the mass conservation equation for blood (Fick principle) and the two diffusion–perfusion interaction equations (Piiper and Scheid 1981; Piiper et al. 1984). At steady state, all these equations must have equal solutions for
) by combining the mass conservation equation for blood (Fick principle) and the two diffusion–perfusion interaction equations (Piiper and Scheid 1981; Piiper et al. 1984). At steady state, all these equations must have equal solutions for 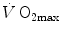 . The algebraic development of the system led to three equations allowing a solution for
. The algebraic development of the system led to three equations allowing a solution for 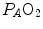 ,
, 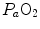 and
and 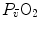 . These equations lead to a unique, necessary
. These equations lead to a unique, necessary 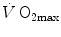 value for any combination of known values of
value for any combination of known values of 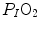 ,
, 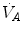 , D L,
, D L, 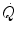 ,
, 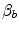 and D t at maximal exercise (Wagner 1993). Wagner’s system of equations implies a vision of the oxygen cascade with two mass balance equations responsible for convective oxygen transfer, associated with two conductive components, described by the diffusion–perfusion interaction equations. This vision is conceptually different from di Prampero’s, who conceived a pure hydraulic system of in-series resistances. Proximally, the interaction of a convective component with a diffusive component sets the maximal flow of oxygen in arterial blood (
and D t at maximal exercise (Wagner 1993). Wagner’s system of equations implies a vision of the oxygen cascade with two mass balance equations responsible for convective oxygen transfer, associated with two conductive components, described by the diffusion–perfusion interaction equations. This vision is conceptually different from di Prampero’s, who conceived a pure hydraulic system of in-series resistances. Proximally, the interaction of a convective component with a diffusive component sets the maximal flow of oxygen in arterial blood (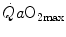 ), and this is the first step in the system. Distally, the interaction of a convective component (Fick principle) with a diffusive component (the diffusion–perfusion interaction equation setting oxygen flow from peripheral capillaries to the muscle fibres) sets
), and this is the first step in the system. Distally, the interaction of a convective component (Fick principle) with a diffusive component (the diffusion–perfusion interaction equation setting oxygen flow from peripheral capillaries to the muscle fibres) sets 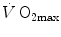 .
.
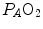 ,
, 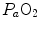 and
and 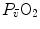 ) by combining the mass conservation equation for blood (Fick principle) and the two diffusion–perfusion interaction equations (Piiper and Scheid 1981; Piiper et al. 1984). At steady state, all these equations must have equal solutions for
) by combining the mass conservation equation for blood (Fick principle) and the two diffusion–perfusion interaction equations (Piiper and Scheid 1981; Piiper et al. 1984). At steady state, all these equations must have equal solutions for 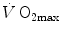 . The algebraic development of the system led to three equations allowing a solution for
. The algebraic development of the system led to three equations allowing a solution for 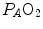 ,
, 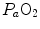 and
and 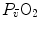 . These equations lead to a unique, necessary
. These equations lead to a unique, necessary 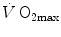 value for any combination of known values of
value for any combination of known values of 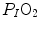 ,
, 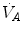 , D L,
, D L, 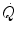 ,
, 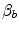 and D t at maximal exercise (Wagner 1993). Wagner’s system of equations implies a vision of the oxygen cascade with two mass balance equations responsible for convective oxygen transfer, associated with two conductive components, described by the diffusion–perfusion interaction equations. This vision is conceptually different from di Prampero’s, who conceived a pure hydraulic system of in-series resistances. Proximally, the interaction of a convective component with a diffusive component sets the maximal flow of oxygen in arterial blood (
and D t at maximal exercise (Wagner 1993). Wagner’s system of equations implies a vision of the oxygen cascade with two mass balance equations responsible for convective oxygen transfer, associated with two conductive components, described by the diffusion–perfusion interaction equations. This vision is conceptually different from di Prampero’s, who conceived a pure hydraulic system of in-series resistances. Proximally, the interaction of a convective component with a diffusive component sets the maximal flow of oxygen in arterial blood (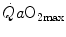 ), and this is the first step in the system. Distally, the interaction of a convective component (Fick principle) with a diffusive component (the diffusion–perfusion interaction equation setting oxygen flow from peripheral capillaries to the muscle fibres) sets
), and this is the first step in the system. Distally, the interaction of a convective component (Fick principle) with a diffusive component (the diffusion–perfusion interaction equation setting oxygen flow from peripheral capillaries to the muscle fibres) sets 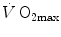 .
.The Fick equation can take either of the following solutions:
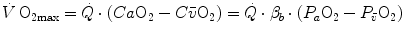
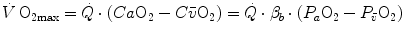
(4.15)
The term 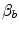 in Eq. (4.15) implies a nonlinear negative relationship between
in Eq. (4.15) implies a nonlinear negative relationship between 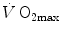 and
and 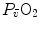 (convective curve), the algebraic expression of which depends on the solution that is given to the oxygen equilibrium curve. Concerning the diffusive component, it is described by the following equation:
(convective curve), the algebraic expression of which depends on the solution that is given to the oxygen equilibrium curve. Concerning the diffusive component, it is described by the following equation:
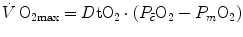
where 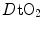 is tissue diffusing capacity for oxygen and
is tissue diffusing capacity for oxygen and 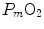 is again equal to 0 mmHg. However, the right branches of Eqs. (4.15) and (4.16) do not share any term, so that they cannot as such be compared on the same plot. To circumvent this obstacle, Wagner assumed direct proportionality between
is again equal to 0 mmHg. However, the right branches of Eqs. (4.15) and (4.16) do not share any term, so that they cannot as such be compared on the same plot. To circumvent this obstacle, Wagner assumed direct proportionality between 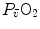 and
and 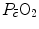 , arguing that the segment of the oxygen equilibrium curve between these two pressure values is essentially linear, so that within that segment
, arguing that the segment of the oxygen equilibrium curve between these two pressure values is essentially linear, so that within that segment 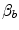 can be considered invariant. On this basis, he reformulated Eq. (4.16) as follows:
can be considered invariant. On this basis, he reformulated Eq. (4.16) as follows:
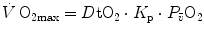
where 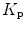 is the dimensionless constant relating
is the dimensionless constant relating 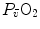 and
and 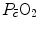 . Equation (4.17) implies a positive linear relationship between
. Equation (4.17) implies a positive linear relationship between 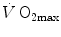 and
and 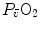 (diffusion line), which Roca et al. (1989) determined experimentally. The slope of the line is equal to the product
(diffusion line), which Roca et al. (1989) determined experimentally. The slope of the line is equal to the product 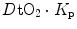 , which Ferretti (2014) called Wagner’s constant,
, which Ferretti (2014) called Wagner’s constant, 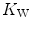 . Equations (4.15) and (4.17) generate analytical relationships that, if we plot
. Equations (4.15) and (4.17) generate analytical relationships that, if we plot 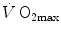 on the y-axis and
on the y-axis and 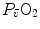 on the x-axis, can be represented on the same graph and directly compared (Fig. 4.5). In this figure, the resulting
on the x-axis, can be represented on the same graph and directly compared (Fig. 4.5). In this figure, the resulting 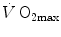 for any combination of
for any combination of 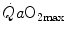 and
and 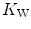 corresponds to the intersection of the two functions, which occurs at a precise value of
corresponds to the intersection of the two functions, which occurs at a precise value of 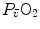 .
.
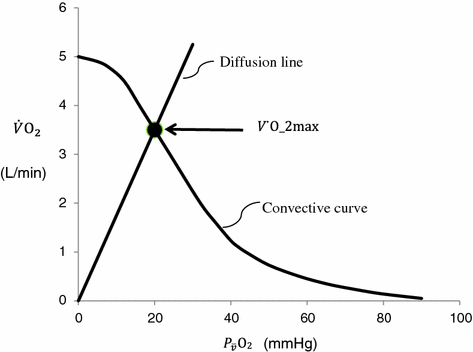
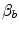 in Eq. (4.15) implies a nonlinear negative relationship between
in Eq. (4.15) implies a nonlinear negative relationship between 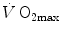 and
and 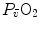 (convective curve), the algebraic expression of which depends on the solution that is given to the oxygen equilibrium curve. Concerning the diffusive component, it is described by the following equation:
(convective curve), the algebraic expression of which depends on the solution that is given to the oxygen equilibrium curve. Concerning the diffusive component, it is described by the following equation: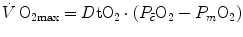
(4.16)
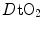 is tissue diffusing capacity for oxygen and
is tissue diffusing capacity for oxygen and 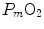 is again equal to 0 mmHg. However, the right branches of Eqs. (4.15) and (4.16) do not share any term, so that they cannot as such be compared on the same plot. To circumvent this obstacle, Wagner assumed direct proportionality between
is again equal to 0 mmHg. However, the right branches of Eqs. (4.15) and (4.16) do not share any term, so that they cannot as such be compared on the same plot. To circumvent this obstacle, Wagner assumed direct proportionality between 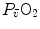 and
and 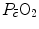 , arguing that the segment of the oxygen equilibrium curve between these two pressure values is essentially linear, so that within that segment
, arguing that the segment of the oxygen equilibrium curve between these two pressure values is essentially linear, so that within that segment 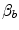 can be considered invariant. On this basis, he reformulated Eq. (4.16) as follows:
can be considered invariant. On this basis, he reformulated Eq. (4.16) as follows: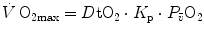
(4.17)
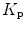 is the dimensionless constant relating
is the dimensionless constant relating 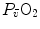 and
and 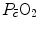 . Equation (4.17) implies a positive linear relationship between
. Equation (4.17) implies a positive linear relationship between 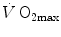 and
and 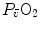 (diffusion line), which Roca et al. (1989) determined experimentally. The slope of the line is equal to the product
(diffusion line), which Roca et al. (1989) determined experimentally. The slope of the line is equal to the product 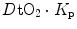 , which Ferretti (2014) called Wagner’s constant,
, which Ferretti (2014) called Wagner’s constant, 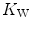 . Equations (4.15) and (4.17) generate analytical relationships that, if we plot
. Equations (4.15) and (4.17) generate analytical relationships that, if we plot 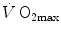 on the y-axis and
on the y-axis and 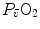 on the x-axis, can be represented on the same graph and directly compared (Fig. 4.5). In this figure, the resulting
on the x-axis, can be represented on the same graph and directly compared (Fig. 4.5). In this figure, the resulting 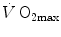 for any combination of
for any combination of 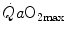 and
and 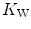 corresponds to the intersection of the two functions, which occurs at a precise value of
corresponds to the intersection of the two functions, which occurs at a precise value of 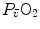 .
.
Fig. 4.5
Graphical representation of Wagner’s model. Oxygen uptake (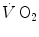 ) is plotted as a function of mixed venous oxygen pressure (
) is plotted as a function of mixed venous oxygen pressure (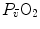 ). The curve with negative slope is Wagner’s convective curve. The straight line with positive slope is Wagner’s diffusion line, whose slope is equal to Wagner’s constant
). The curve with negative slope is Wagner’s convective curve. The straight line with positive slope is Wagner’s diffusion line, whose slope is equal to Wagner’s constant 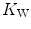 . The convective curve intercepts the y-axis at a
. The convective curve intercepts the y-axis at a 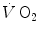 equal to arterial oxygen flow (
equal to arterial oxygen flow (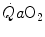 ), which is the case when
), which is the case when 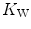 = ∞. The same curve intercepts the x-axis when
= ∞. The same curve intercepts the x-axis when 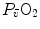 is equal to arterial oxygen pressure, which is the case when
is equal to arterial oxygen pressure, which is the case when 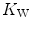 = 0. The
= 0. The 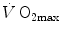 value is found on the crossing of the convective curve with the diffusion line (full dot). After Ferretti (2014)
value is found on the crossing of the convective curve with the diffusion line (full dot). After Ferretti (2014)
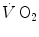 ) is plotted as a function of mixed venous oxygen pressure (
) is plotted as a function of mixed venous oxygen pressure (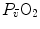 ). The curve with negative slope is Wagner’s convective curve. The straight line with positive slope is Wagner’s diffusion line, whose slope is equal to Wagner’s constant
). The curve with negative slope is Wagner’s convective curve. The straight line with positive slope is Wagner’s diffusion line, whose slope is equal to Wagner’s constant 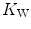 . The convective curve intercepts the y-axis at a
. The convective curve intercepts the y-axis at a 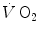 equal to arterial oxygen flow (
equal to arterial oxygen flow (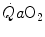 ), which is the case when
), which is the case when 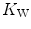 = ∞. The same curve intercepts the x-axis when
= ∞. The same curve intercepts the x-axis when 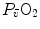 is equal to arterial oxygen pressure, which is the case when
is equal to arterial oxygen pressure, which is the case when 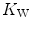 = 0. The
= 0. The 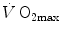 value is found on the crossing of the convective curve with the diffusion line (full dot). After Ferretti (2014)
value is found on the crossing of the convective curve with the diffusion line (full dot). After Ferretti (2014)Experimental Testing of Wagner’s Model
Concerning the diffusive component, a decrease in 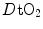 implies, in Fig. 4.5, a decrease in
implies, in Fig. 4.5, a decrease in 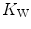 , whence a drop of
, whence a drop of 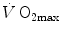 and an increase in
and an increase in 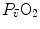 . The reverse is caused by an increase in
. The reverse is caused by an increase in 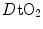 . This is virtually impossible to test in humans with acute manoeuvres acting on
. This is virtually impossible to test in humans with acute manoeuvres acting on 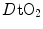 , the most important determinant of
, the most important determinant of 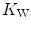 . Moreover,
. Moreover, 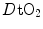 is affected by haemoglobin concentration (Schaffartzik et al. 1993). Wagner (1996a) predicted quite accurately the effects of chronic alterations of
is affected by haemoglobin concentration (Schaffartzik et al. 1993). Wagner (1996a) predicted quite accurately the effects of chronic alterations of 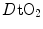 on
on 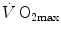 and
and 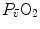 in patients affected by chronic obstructive pulmonary disease, once allowance was made for the simultaneous impairment of cardiovascular oxygen transport. If direct proportionality between
in patients affected by chronic obstructive pulmonary disease, once allowance was made for the simultaneous impairment of cardiovascular oxygen transport. If direct proportionality between 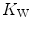 and muscle capillary density is assumed, an analysis of literature data of muscle morphometry and
and muscle capillary density is assumed, an analysis of literature data of muscle morphometry and 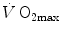 of altitude-acclimatized climbers (Hoppeler et al. 1990; Oelz et al. 1986) or endurance-trained subjects (Hoppeler et al. 1985) led to
of altitude-acclimatized climbers (Hoppeler et al. 1990; Oelz et al. 1986) or endurance-trained subjects (Hoppeler et al. 1985) led to 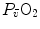 values coherent with Wagner’s predictions (Ferretti 2014).
values coherent with Wagner’s predictions (Ferretti 2014).
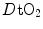 implies, in Fig. 4.5, a decrease in
implies, in Fig. 4.5, a decrease in 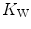 , whence a drop of
, whence a drop of 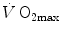 and an increase in
and an increase in 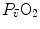 . The reverse is caused by an increase in
. The reverse is caused by an increase in 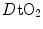 . This is virtually impossible to test in humans with acute manoeuvres acting on
. This is virtually impossible to test in humans with acute manoeuvres acting on 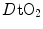 , the most important determinant of
, the most important determinant of 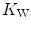 . Moreover,
. Moreover, 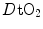 is affected by haemoglobin concentration (Schaffartzik et al. 1993). Wagner (1996a) predicted quite accurately the effects of chronic alterations of
is affected by haemoglobin concentration (Schaffartzik et al. 1993). Wagner (1996a) predicted quite accurately the effects of chronic alterations of 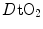 on
on 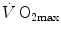 and
and 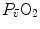 in patients affected by chronic obstructive pulmonary disease, once allowance was made for the simultaneous impairment of cardiovascular oxygen transport. If direct proportionality between
in patients affected by chronic obstructive pulmonary disease, once allowance was made for the simultaneous impairment of cardiovascular oxygen transport. If direct proportionality between 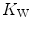 and muscle capillary density is assumed, an analysis of literature data of muscle morphometry and
and muscle capillary density is assumed, an analysis of literature data of muscle morphometry and 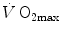 of altitude-acclimatized climbers (Hoppeler et al. 1990; Oelz et al. 1986) or endurance-trained subjects (Hoppeler et al. 1985) led to
of altitude-acclimatized climbers (Hoppeler et al. 1990; Oelz et al. 1986) or endurance-trained subjects (Hoppeler et al. 1985) led to 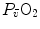 values coherent with Wagner’s predictions (Ferretti 2014).
values coherent with Wagner’s predictions (Ferretti 2014).On the convective curve, an increase in the product of 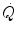 times
times 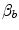 carries along an increase in both
carries along an increase in both 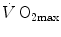 and
and 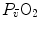 . This explains, in Wagner’s model, the effects of acute polycythaemia and anaemia on
. This explains, in Wagner’s model, the effects of acute polycythaemia and anaemia on 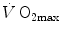 (Ekblom et al. 1976; Woodson et al. 1978): the convective curve is displaced upwards and becomes steeper. The intercept on the x-axis of the convective curve corresponds to the
(Ekblom et al. 1976; Woodson et al. 1978): the convective curve is displaced upwards and becomes steeper. The intercept on the x-axis of the convective curve corresponds to the 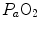 point, i.e. the point at which
point, i.e. the point at which 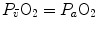 . Hyperoxia displaces this point to the right, implying a slightly higher
. Hyperoxia displaces this point to the right, implying a slightly higher 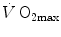 , because the rightward displacement of the
, because the rightward displacement of the 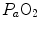 point increases the slope of the convective curve (makes it less negative), so that the diffusion line is intercepted at a higher
point increases the slope of the convective curve (makes it less negative), so that the diffusion line is intercepted at a higher 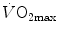 value. The reverse occurs in hypoxia. The y-intercept of the convective curve corresponds to the
value. The reverse occurs in hypoxia. The y-intercept of the convective curve corresponds to the 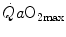 point, representing the condition in which
point, representing the condition in which 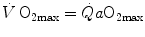 (Wagner 1995, 1996a). The case of hypoxia is treated in a separate paragraph (see Of Maximal Oxygen Consumption in Hypoxia). Controversial is the case of hyperoxia. Although Fig. 4.5 predicts an increase in
(Wagner 1995, 1996a). The case of hypoxia is treated in a separate paragraph (see Of Maximal Oxygen Consumption in Hypoxia). Controversial is the case of hyperoxia. Although Fig. 4.5 predicts an increase in 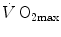 , such an increase was rarely observed in humans, the only clear effects having been observed in individuals with elevated
, such an increase was rarely observed in humans, the only clear effects having been observed in individuals with elevated 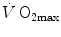 , who are subject to the Dempsey effect (Dempsey and Wagner 1999; Dempsey et al. 1984; Powers et al. 1989). Richardson et al. (1999) were able to observe a
, who are subject to the Dempsey effect (Dempsey and Wagner 1999; Dempsey et al. 1984; Powers et al. 1989). Richardson et al. (1999) were able to observe a 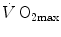 increase during single-leg exercise only when they used pure oxygen breathing. The thoroughbred horse, a highly athletic animal characterized by deep hypoxaemia at maximal exercise, was proposed as the nicest example supporting the prediction of elevated
increase during single-leg exercise only when they used pure oxygen breathing. The thoroughbred horse, a highly athletic animal characterized by deep hypoxaemia at maximal exercise, was proposed as the nicest example supporting the prediction of elevated 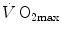 in hyperoxia (Wagner 1996a; Wagner et al. 1989, 1996). This apparent discrepancy between theoretical predictions and experimental data is hard to explain, and the hypotheses put forward so far are scarcely convincing, so that the issue still remains open.
in hyperoxia (Wagner 1996a; Wagner et al. 1989, 1996). This apparent discrepancy between theoretical predictions and experimental data is hard to explain, and the hypotheses put forward so far are scarcely convincing, so that the issue still remains open.
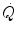 times
times 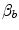 carries along an increase in both
carries along an increase in both 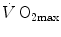 and
and 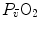 . This explains, in Wagner’s model, the effects of acute polycythaemia and anaemia on
. This explains, in Wagner’s model, the effects of acute polycythaemia and anaemia on 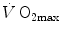 (Ekblom et al. 1976; Woodson et al. 1978): the convective curve is displaced upwards and becomes steeper. The intercept on the x-axis of the convective curve corresponds to the
(Ekblom et al. 1976; Woodson et al. 1978): the convective curve is displaced upwards and becomes steeper. The intercept on the x-axis of the convective curve corresponds to the 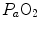 point, i.e. the point at which
point, i.e. the point at which 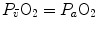 . Hyperoxia displaces this point to the right, implying a slightly higher
. Hyperoxia displaces this point to the right, implying a slightly higher 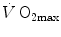 , because the rightward displacement of the
, because the rightward displacement of the 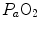 point increases the slope of the convective curve (makes it less negative), so that the diffusion line is intercepted at a higher
point increases the slope of the convective curve (makes it less negative), so that the diffusion line is intercepted at a higher 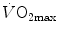 value. The reverse occurs in hypoxia. The y-intercept of the convective curve corresponds to the
value. The reverse occurs in hypoxia. The y-intercept of the convective curve corresponds to the 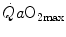 point, representing the condition in which
point, representing the condition in which 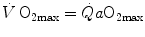 (Wagner 1995, 1996a). The case of hypoxia is treated in a separate paragraph (see Of Maximal Oxygen Consumption in Hypoxia). Controversial is the case of hyperoxia. Although Fig. 4.5 predicts an increase in
(Wagner 1995, 1996a). The case of hypoxia is treated in a separate paragraph (see Of Maximal Oxygen Consumption in Hypoxia). Controversial is the case of hyperoxia. Although Fig. 4.5 predicts an increase in 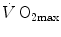 , such an increase was rarely observed in humans, the only clear effects having been observed in individuals with elevated
, such an increase was rarely observed in humans, the only clear effects having been observed in individuals with elevated 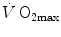 , who are subject to the Dempsey effect (Dempsey and Wagner 1999; Dempsey et al. 1984; Powers et al. 1989). Richardson et al. (1999) were able to observe a
, who are subject to the Dempsey effect (Dempsey and Wagner 1999; Dempsey et al. 1984; Powers et al. 1989). Richardson et al. (1999) were able to observe a 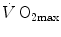 increase during single-leg exercise only when they used pure oxygen breathing. The thoroughbred horse, a highly athletic animal characterized by deep hypoxaemia at maximal exercise, was proposed as the nicest example supporting the prediction of elevated
increase during single-leg exercise only when they used pure oxygen breathing. The thoroughbred horse, a highly athletic animal characterized by deep hypoxaemia at maximal exercise, was proposed as the nicest example supporting the prediction of elevated 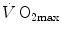 in hyperoxia (Wagner 1996a; Wagner et al. 1989, 1996). This apparent discrepancy between theoretical predictions and experimental data is hard to explain, and the hypotheses put forward so far are scarcely convincing, so that the issue still remains open.
in hyperoxia (Wagner 1996a; Wagner et al. 1989, 1996). This apparent discrepancy between theoretical predictions and experimental data is hard to explain, and the hypotheses put forward so far are scarcely convincing, so that the issue still remains open.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree