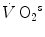(1.1)
where E, P, V and T stand for energy, pressure, volume and temperature (expressed in °C), n represents the amount of gas, currently expressed in moles, and R indicates the amount of energy introduced into 1 mol of gas by a unit increase in temperature, corresponding to the slope of the linear relationship for n = 1 in Fig. 1.1. Constant T 0, which appears in Fig. 1.1 as the x-axis intercept on which all isopleths for n converge, is the temperature at which E = 0 J. It corresponds to −273.14 °C and was called the absolute zero. When Lord William Kelvin (1824–1907) set this temperature equal to zero—in practice, in Fig. 1.1, he shifted the x-axis intercept rightwards to have it coinciding with the origin of the axes— he gave origin to the absolute temperature scale, named in his honour. This very simple operation implies that, if in Eq. (1.1) we express temperature in absolute scale (Kelvin degrees, °K) instead than in centigrade scale, we obtain the following:
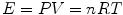
(1.1a)
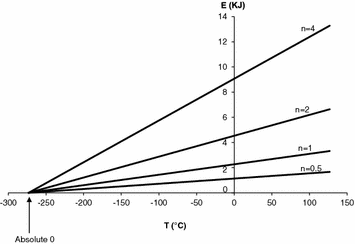
Fig. 1.1
Relationship between energy (E, in kJ), i.e. the product of pressure times volume, and temperature (T, in °C) for given quantities of gas. Straight lines for the four indicated molar amounts of gas (n) are reported. The slope of the line for n = 1 yields what was called the universal constant of perfect gases (R). The x-axis intercept indicates the temperature at which E = 0 kJ, which was defined as the absolute zero. Taken from Ferretti and Capelli (2008)
In fact, Eq. (1.1a) sets a relation of direct proportionality between energy and temperature, which allowed reintroducing heat in the game as a form of energy. More than a century later, since for any given quantity of gas:
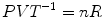
which is a constant, Eqs. (1.1a) and (1.1b) provided the physical basis for the criteria of quantitative standardization for gas volumes and flows, which were established by the American Physiological Society. Two standard conditions for volume measurement comparisons were defined, one called BTPS—body temperature (37 °C or 310 °K) and pressure (barometric pressure of the day), saturated with water vapour (47 mmHg at 37 °C)—the other called STPD—standard temperature (0 °C or 273 °K) and pressure (760 mmHg), dry. Conventionally, the former is used for standardizing volumes and flows of overall gas mixtures such as air, so that pulmonary ventilation or lung volumes are expressed in BTPS condition and the latter is employed for flows or volumes of a single pure gas (American Physiological Society 1950). This convention is respected in this book.
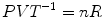
(1.1b)
Despite the fact that about a century earlier John Mayhow (1643–1679) had already perceived that muscle work involved some kind of “nitro-aerial” component of air, the processes of respiration and metabolism started to be seen in a little bit clearer way only after Joseph Black (1728–1799) had “discovered” carbon dioxide in 1764, which he called “fixed air”, and which he realized to be liberated by respiration, and Joseph Priestley (1733–1804) had “discovered” oxygen in 1774, which he called “dephlogisticated air”, which means air free from phlogiston (see below). Shortly afterwards, Antoine Lavoisier (1743–1794), who coined the name oxygen, realized that this gas was not only essential to human life, for humans consume oxygen, but was essential also to human locomotion and exercise, for he demonstrated that oxygen consumption (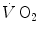 ) increased when a man exercised. Moreover, together with Armand Séguin (1767–1835), he showed that exercise was associated also with an increased elimination of carbon dioxide and an increased production of heat. These observations implied that the chemical energy transformation supporting the production of mechanical energy in muscle contraction was a process of combustion, in which oxygen played the role of oxidizer, and carbon dioxide was the end product.
) increased when a man exercised. Moreover, together with Armand Séguin (1767–1835), he showed that exercise was associated also with an increased elimination of carbon dioxide and an increased production of heat. These observations implied that the chemical energy transformation supporting the production of mechanical energy in muscle contraction was a process of combustion, in which oxygen played the role of oxidizer, and carbon dioxide was the end product.
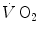 ) increased when a man exercised. Moreover, together with Armand Séguin (1767–1835), he showed that exercise was associated also with an increased elimination of carbon dioxide and an increased production of heat. These observations implied that the chemical energy transformation supporting the production of mechanical energy in muscle contraction was a process of combustion, in which oxygen played the role of oxidizer, and carbon dioxide was the end product.
) increased when a man exercised. Moreover, together with Armand Séguin (1767–1835), he showed that exercise was associated also with an increased elimination of carbon dioxide and an increased production of heat. These observations implied that the chemical energy transformation supporting the production of mechanical energy in muscle contraction was a process of combustion, in which oxygen played the role of oxidizer, and carbon dioxide was the end product.This conclusion had two conceptual consequences: (1) the process of chemical energy transformation requires oxidation of an organic fuel, and (2) a tight match between oxygen consumption and fuel degradation must be in place. But no idea existed about the chemical transformations at stake and the way this matching could take place. In fact, Lavoisier was convinced that combustion took place in the lungs and that the heat produced during combustion was taken away by means of blood circulation. Adair Crawford (1748–1795), a pupil of Joseph Black, put forward another curious theory of animal heat, which in modern terms can be summarized as follows: the oxygen contained in ambient air gives up its heat as it is converted into carbon dioxide in the lungs; the heat liberated by oxygen transformation does not lead to an increase in lung temperature, because of differences in the specific heat of arterial and venous blood, such that the blood in the pulmonary vein undergoes an increase in specific heat as a consequence of heat exchange from the lung. To explain these “events”, Crawford resurrected the phlogistic theory, created by Georg Ernst Stahl (1660–1734), according to which combustibles consisted of ash combined with a fire principle, the “phlogiston”, which was liberated during burning: fire could not be maintained in closed spaces because air became saturated with phlogiston. Crawford believed that the action of phlogiston prompted the alleged heat exchange between lungs and arterial blood, despite Lavoisier had already falsified the phlogiston theory by means of his demonstration that combustion was the result of a combination of a fuel with oxygen. A nice example indeed of how difficult is to discard by means of experimental falsification a theory that has become a belief.
The identification of oxygen and carbon dioxide had a huge impact also in another sense, since it provided a demonstration that air is not a “pure” gas, but a mixture of different gases, some of which were essential for life. Priestley had already shown that oxygen was one of the chemical components of air. Yet, and surprisingly enough in those times, the most abundant gas in air was neither oxygen nor carbon dioxide, but nitrogen, whose identification is generally attributed to Daniel Rutherford (1749–1819), although its existence had already been perceived by Priestley, Scheele and Cavendish, and although Rutherford did not realize it was a pure gas, but thought it was air saturated with phlogiston. It was once more Lavoisier, perhaps the greatest genius of the classical epopee of gas chemistry, who first recognized nitrogen to be a pure gas and realized that air was a mixture of at least an “active” gas (oxygen), sustaining combustion and respiration, and an “inactive” gas, nitrogen, fully inert with respect to respiration. Subsequently, the study of gas mixtures led John Dalton (1766–1844) to define the independent behaviour of single gases in a mixture, whose quantitative description is called Dalton’s law, and to create the concepts of partial pressure of a gas and of gas fraction. With time, several other inert components of air were identified and quantitated. What is currently considered the normal composition of dry atmospheric air is reported in Table 1.1. In respiratory and exercise physiology, in view of their very small fraction in air composition, inert gases other than nitrogen are normally neglected.
Table 1.1
Fractional composition of dry air, and the corresponding partial pressures, at the indicated altitudes above or depths below sea level
O2 | CO2 | N2 | Other gases | Atmosphere | Atmosphere | |
|---|---|---|---|---|---|---|
Gas fraction | 0.2094 | 0.0003 | 0.78 | 0.0103 | 1 | 1 |
Gas pressure | PO2 (mmHg) | PCO2 (mmHg) | PN2 (mmHg) | P gas (mmHg) | P (mmHg) | P (Atm) |
Top of Mount Everest (8848 m) | 53.0 | 0.08 | 197 | 2.6 | 253 | 0.3 |
Top of Mont Blanc (4810 m) | 90.0 | 0.13 | 335 | 4.4 | 430 | 0.6 |
La Paz, Bolivia (3600 m) | 104.7 | 0.15 | 390 | 5.1 | 500 | 0.7 |
Mexico City (2200 m) | 121.5 | 0.17 | 452 | 6.0 | 580 | 0.8 |
Sea level | 159.1 | 0.23 | 593 | 7.8 | 760 | 1.0 |
Depth—10 m | 318.3 | 0.46 | 1186 | 15.7 | 1520 | 2.0 |
Depth—20 m | 477.4 | 0.68 | 1778 | 23.5 | 2280 | 3.0 |
Depth—50 m | 954.9 | 1.37 | 3557 | 47.0 | 4560 | 6.0 |
Depth—100 m | 1750.6 | 2.51 | 6521 | 86.1 | 8360 | 11.0 |
Depth—300 m | 4933.5 | 7.07 | 18,377 | 242.7 | 23,560 | 31.0 |
The partial pressure of a given gas in air, when air is exposed to a liquid, is the force that pushes that gas to dissolve into the liquid. The amount of gas entering the liquid is exactly the one that is necessary to counterbalance the action of external partial pressure. This led William Henry (1774–1836) to establish the relation of direct proportionality between gas pressure and gas concentration in a liquid. On this basis, the partial pressure of a gas in a liquid (e.g. blood) was defined as the pressure that is necessary to keep a given gas concentration in that very liquid. The law of Henry sets the physical context for otherwise bizarre expressions such as “oxygen partial pressure in arterial blood”, as long as there is no column of oxygen above arterial blood and actually compressing it directly.
Of Energy and Work
At the beginning of the nineteenth century, the identification of heat as a form of energy led to the creation of a new branch of chemistry, now called thermodynamics. In this context, the law of energy conservation states that in a close thermodynamic system, the overall amount of energy is a constant. The internal energy of a part of the system can thus vary only if there is energy transfer in or out that part of the system. Spontaneously, any thermodynamic system tends to a condition of equilibrium. This equilibrium, however, is not necessarily attained at the state where the system possesses the minimum amount of energy. Two tendencies coexist, one moving towards a state of minimal energy and the other moving towards a state of maximal disorder. The former tendency is reflected by the variations of enthalpy (H, in J). In a reaction occurring at constant pressure and volume, the variations of enthalpy correspond to the heat (Θ) that is liberated (negative sign, spontaneous exergonic reaction) or absorbed (positive sign, endergonic reaction) by the system. The latter tendency is reflected by the variations of entropy (S, in J K−1), which is the constant characterizing the relationship between heat and temperature. Entropy is qualitatively defined as the tendency of a system to evolve towards a state of greater “disorder”. The equilibrium between these two tendencies is defined by their combination in the following form:
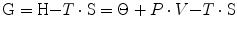
where G is the overall energy possessed by a given part of the system and is termed Gibbs free energy, in honour of Willard Gibbs (1839–1903), who created the concept of entropy and defined the equilibrium between enthalpy and entropy in 1874–1878. A consequence of Eq. (1.2) is that any chemical reaction proceeds spontaneously as long as the tendency is towards the attainment of minimal G. G cannot be measured in absolute terms, but we can measure its variations in the course of a chemical reaction. The variations are generally measured in a standard condition (1 M at 25 °C and 760 mmHg), designated with suffix 0:
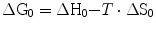
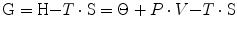
(1.2)
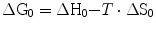
(1.2a)
In 1847, Hermann Ludwig von Helmholtz (1821–1894) demonstrated that the law of energy conservation applies also to living organisms, including man (Atwater 1904). This implied that Eq. (1.2) applies to all chemical reactions occurring in humans. Keeping a human alive requires increasing his amount of G, while death implies a decrease in G. This explains why life requires continuous introduction of energy from outside into the living system. Moreover, all reactions characterised by an increase in G necessitate external energy supporting them.
Meanwhile, the development of the first techniques of motion pictures, anticipating the birth of the cinematograph, allowed Etienne-Jules Marey (1830–1904) and Georges Demény (1850–1917) to carry out the first mechanical analyses of human locomotion. These authors established the principles on which Wallace Fenn (1893–1971) constructed the laws of human motion, which are still applied nowadays in the study of human locomotion, and created the concepts of external and internal work (Fenn 1930).
The advancements in optical microscopy led also to the first structural descriptions of muscle fibres. Already in 1781, Felice Fontana (1730–1805) realized that muscle fibres consisted of fascicles of many cylinders disposed in series, with regular indentations that conferred an aspect of striation. William Bowman (1816–1892) demonstrated that these cylinders consisted of compact bundles of parallel fibrils, enclosed by a thin membrane that he called sarcolemma (Frixione 2006). From fibrils, in 1864, Wilhelm Kühne (1836–1900) extracted a protein, which he called myosin. The ATP-ase activity of myosin was demonstrated only (Engelhardt and Lyubimova 1939) after Kurt Lohmann (1898–1978) had identified, in 1928, a new type of high-energy organic phosphate called adenosine-tri-phosphate (ATP), and had demonstrated, in 1934, that this was the essential energy provider for muscular contraction. Louis-Antoine Ranvier (1835–1922) recognized, in 1873, two different types of muscle fibres, “white” and “red”, with different structural and functional characteristics, the latter being rich with mitochondria and filled with a pigment called myoglobin and contracting at slow speed. Actin entered the game in 1943, thanks to the work of Albert Szent-György (1893–1986) and Bruno Ferenc Straub (1914–1996). The former was awarded the Nobel Prize for Physiology and Medicine in 1937 for his contributions to the understanding of the metabolism of ascorbic acid (C vitamin). By 1945, all bricks were in place to allow the conclusion, undisputed ever since, that the energy transfer during muscular contraction was to come from ATP hydrolysis with the liberation of one mole of inorganic phosphate per mole of ATP split. On a somewhat longer time scale, reversal of this reaction implied phosphorylation of adenosine diphosphate (ADP) by the transfer of inorganic phosphate from phosphocreatine (Lohmann’s reaction). The concentration of phosphocreatine was then maintained or restored by the organic phosphates generated in glycolysis and oxidative metabolism. The mechanisms of work generation were underpinned a few years later, after the developments in electron microscopy. Beside confirming several histological observations of the nineteenth century meanwhile forgotten (Huxley 1978), the use of electron microscopy allowed the identification of the sliding process of intermingled thick and thin filaments in the sarcomere (Hanson and Huxley 1953; Huxley 1953; Huxley and Niedergerke 1954; Huxley and Hanson 1954). These structural observations led Sir Andrew Huxley (1918–2013), who was awarded the Nobel Prize for Physiology or Medicine in 1963 for his contribution to our understanding of action potential generation and transmission in nerve axons, to formulate the sliding filament theory, or cross-bridge theory, of muscular contraction (Gordon et al. 1966; Huxley 1957, 1974). A nice history of the events that led to the sliding filament theory was published by Huxley himself (Huxley 1978). ATP hydrolysis is integrated in the theory as the chemical reaction yielding, through the cross-bridge cycle, the energy allowing the shortening of the sarcomere during contraction. For details on the mechanisms of muscle contraction, a reader can refer to several fine reviews (Goldman 1987; Gordon et al. 2000; Huxley 2000).
Oxidative and Anaerobic Metabolism
The question of what could be the fuel supporting the combustion process that generates mechanical energy for locomotion and movement started to receive an answer after the chemical experiments on aliments of the first half of the nineteenth century, when carbohydrates and fatty acids were identified by Justus von Liebig (1803–1873) and Michel Eugène Chevreul (1786–1889). The evolution of chemical knowledge afterwards progressively led to the definition of the main biochemical pathways of intermediate metabolism, and particularly glycolysis [by Otto Fritz Meyerhof (1884–1951), Nobel Prize winner for Physiology or Medicine in 1922] (Meyerhof 1921, 1924), the Krebs cycle [by Hans Krebs (1900–1981), Nobel Prize winner for Physiology or Medicine in 1953, and Hans Kornberg] (Krebs and Kornberg 1957), the beta oxidation of fatty acids and the oxidative phosphorylation in the electron transport chain.
The definition of these fundamental pathways was not the result of a discovery made by a genius. Meyerhof and Krebs made the final synthesis out of a process lasting tenths of years and implying the work of several scientists from numerous laboratories who defined the single steps and described the various chemical components of each pathway. Concerning beta oxidation, this work of synthesis was carried out mainly by Beinert (1963); for oxidative phosphorylation, we are indebted mainly to Peter Mitchell, Nobel Prize winner for Physiology or Medicine in 1978, and to David Keilin (Mitchell 1979). The ensemble of these pathways constitutes the biochemical basis of what is nowadays known as oxidative metabolism. Oxidative metabolism explains exhaustively the links between substrates (fuel) and oxygen (oxidiser) and the tight coupling between oxygen consumption and carbon dioxide production, since carbon dioxide is a major side product of the combustion process. Those who are interested in the historical details of this epopee can refer to various reviews on the subject (Ghisla 2004; Kornberg 2000; Krebs 1970; Mitchell 2004, 2011; Racker 1983).
Glycolysis was the first biochemical pathway of intermediate metabolism to be fully described. The process of formation of lactate as a results of glycolysis, through the reduction of pyruvate, which can be looked at as the end point of the glycolytic pathway, was already inserted in a coherent picture by 1927, although several details were still to be identified (Meyerhof and Lohmann 1927). Six years later, the overall glycolytic pathway was elucidated (Embden et al. 1933). The growing knowledge on glycolysis had a great impact on the early development of exercise physiology and specifically of the energetics of muscular exercise. After Fletcher and Hopkins (1907) demonstrated that lactic acid, an end product of glycolysis, accumulates in contracting muscles, Archibald Vivian Hill (1886–1977), who shared with Otto Meyerhof the 1922 Nobel Prize for Physiology or Medicine, formulated in 1924 the first systematic theory of the energetics of muscular contraction (Hill 1924). According to this theory, the main energy source for muscle contraction is the oxidation of glycogen to lactic acid through glycolysis: oxygen consumption intervenes at a later stage, during recovery, to ensure the complete oxidation of a fraction of the accumulated lactic acid, allowing for the resynthesis of glycogen from the remainder of lactic acid. In this context, Hill created the term oxygen debt to define the volume of oxygen consumed to this aim.
When Hill formulated his theory of the energetics of muscular exercise, lactic acid was well known since long. It was originally identified by Carl Wilhelm Scheele (1742–1786), who isolated it from sour milk as impure brown syrup. It was soon recognized as an important chemical component of living organisms. In 1808, Jöns Jacob Berzelius (1779–1848) demonstrated that lactic acid is produced in muscles during contraction. He also identified pyruvic acid in 1835. The structure was established by Johannes Wislicenus (1835–1902) in 1873. The structure of the enzyme catalysing the reduction of pyruvate to form lactate, then called lactate dehydrogenase, was fully described in 1933 (Andersson 1933).
The reversible reduction of pyruvate into lactate was the chemical keystone of Hill’s theory. The biochemical foundation of the theory implied glycogen oxidation to pyruvate that, during muscle contraction, is converted into lactate. At the end of exercise, pyruvate synthesis falls and the equilibrium of the reaction is inverted to the oxidation of lactate—accumulated in excess—into pyruvate. Of this, part is further oxidized by the Krebs cycle in order to generate the energy sustaining the endergonic process of glycogen resynthesis.
Hill’s theory of the energetics of muscular exercise did not establish a clear distinction between aerobic and anaerobic metabolism. Whereas the energy balance during muscle contraction was seen as an essentially anaerobic process, centred on lactate synthesis and accumulation, the energy balance during recovery was seen as an aerobic process, for oxygen consumption was thought to be necessary to glycogen resynthesis. The cycle was closed by the combination of the two processes. Moreover, a crucial step was missing that related to the transformation of chemical energy into mechanical work. The further evolution of biochemical knowledge bridged this gap and undermined Hill’s theory. A new actor was entering the scene: phosphate.
Already in 1922, Embden and Lawaczek observed that the concentration of inorganic phosphate increases during muscle contraction, suggesting the hypothesis that some phosphate-containing compound, called “phosphagen”, might play a key role in the conversion of chemical energy into mechanical energy. Soon, the concept of phosphagen was related to a new substance that had been identified in muscle: phosphocreatine (Eggleton and Eggleton 1927). The fall of phosphocreatine concentration in muscle following contraction (Nachmanson 1928) was soon associated with the increase in inorganic phosphate. Was phosphocreatine the phosphagen? The observation by Lundsgaard (1930) that a muscle poisoned with mono-iodo-acetic acid can contract without lactic acid accumulation seemed to give a positive answer to this question, by excluding lactate as a necessary chemical intermediate of muscle contraction. But this was not so. Kurt Lohmann (1898–1978), who in 1928 had identified a new type of high-energy organic phosphate called adenosine-tri-phosphate (ATP) (Lohmann 1928), demonstrated in 1934 that this was the essential energy provider for muscular contraction (Lohmann 1934). The demonstration of the ATP-ase activity of myosin (Engelhardt and Lyubimova 1939) provided a potential direct mechanism for the conversion of chemical energy stored in ATP into mechanical work.
Hill understood that the appearance of phosphagen, or more in general phosphates, on the scene could undermine his vision. He was a real scientist and accepted the risk of refutation. In 1932, he wrote a marvellous review (Hill 1932), in which, from a “loser” perspective, he announced a “revolution” in muscle physiology and tried to defend his theory by integrating the new ideas in it—pretty much as Necker, prime minister of King Louis XVI, tried to do at the onset of the French revolution in 1789. This is a text that every physiologist should read to take a lesson of humility and intellectual honesty. However, it was not phosphate that killed Hill’s theory. Phosphate could in principle be accommodated in Hill’s theory by considering it as the link between the chemical pathway and the contractile unit in muscle fibres.
Refutation of Hill’s theory was provided by Rodolfo Margaria (1901–1983) and David Bruce Dill (1891–1986) (see Fig. 1.2) on a totally different basis, before the understanding of the role of ATP in muscular contraction. Hill’s theory predicted that during recovery after exercise, if oxygen is consumed to remove the lactate accumulated during muscle contractions, there must be parallelism between lactate disappearance from blood and oxygen consumption. Margaria et al. (1933), in a classical paper that set basis for most of the subsequent developments in the field, demonstrated that the kinetics of 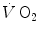 during recovery after exercise differs from that of lactate removal, the former being much faster than the latter (half time of ~40 s vs. ~15 min, respectively), thus being acquitted from the charge of responsibility in lactate removal. Moreover, the demonstration that during light exercise there is an increase in
during recovery after exercise differs from that of lactate removal, the former being much faster than the latter (half time of ~40 s vs. ~15 min, respectively), thus being acquitted from the charge of responsibility in lactate removal. Moreover, the demonstration that during light exercise there is an increase in 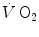 in the absence of lactate accumulation provided the final dissociation of the two and led to the recognition of oxygen consumption as a direct energy source for muscular exercise.
in the absence of lactate accumulation provided the final dissociation of the two and led to the recognition of oxygen consumption as a direct energy source for muscular exercise.

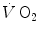 during recovery after exercise differs from that of lactate removal, the former being much faster than the latter (half time of ~40 s vs. ~15 min, respectively), thus being acquitted from the charge of responsibility in lactate removal. Moreover, the demonstration that during light exercise there is an increase in
during recovery after exercise differs from that of lactate removal, the former being much faster than the latter (half time of ~40 s vs. ~15 min, respectively), thus being acquitted from the charge of responsibility in lactate removal. Moreover, the demonstration that during light exercise there is an increase in 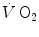 in the absence of lactate accumulation provided the final dissociation of the two and led to the recognition of oxygen consumption as a direct energy source for muscular exercise.
in the absence of lactate accumulation provided the final dissociation of the two and led to the recognition of oxygen consumption as a direct energy source for muscular exercise.
Fig. 1.2
Portrait of Rodolfo Margaria (left) with David Bruce Dill. They were co-authors of the celebrated 1933 paper in which refutation of Hill’s theory of the energetics of muscular exercise was provided. The paternity of the idea was recognized to Margaria by Dill himself
Margaria was the first to talk of different, yet concomitant metabolisms during exercise, namely aerobic metabolism, sustaining light exercise for long periods of time, and anaerobic metabolism, sustaining explosive exercise but for short periods of time. He later corrected his view by including phosphagen and the resynthesis of ATP from the Lohmann’s reaction in the picture and splitting the concept of anaerobic metabolism in two: anaerobic lactic metabolism, implying lactate accumulation in blood, and anaerobic alactic metabolism, centred on the ATP resynthesis from phosphocreatine without lactate accumulation. The latter accounts for explosive efforts of few seconds duration. In his view, each metabolism was characterized by a maximal capacity—maximal amount of energy that it can provide—and by a maximal power. Maximal oxygen consumption was identified as the maximal power attained by aerobic metabolism. He defined the maximal lactic power as the power yielding the maximal rate of blood lactate accumulation (he said production, Margaria et al. 1964). This definition implied the concept of an energy equivalent of blood lactate accumulation (Margaria et al. 1963). More generally speaking, Margaria was convinced, and rightly enough in my opinion, that there must be a relationship of direct proportionality between the variables characterizing each metabolism—steady state 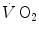 for aerobic metabolism, rate of increase in blood lactate concentration for anaerobic lactic metabolism, rate of decrease in muscle phosphocreatine concentration for anaerobic alactic metabolism—and the rate of energy delivery (metabolic power) of each metabolism. The maximal powers and capacities and the corresponding energy equivalents, as reported by di Prampero (1981), are shown in Table 1.2.
for aerobic metabolism, rate of increase in blood lactate concentration for anaerobic lactic metabolism, rate of decrease in muscle phosphocreatine concentration for anaerobic alactic metabolism—and the rate of energy delivery (metabolic power) of each metabolism. The maximal powers and capacities and the corresponding energy equivalents, as reported by di Prampero (1981), are shown in Table 1.2.
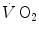 for aerobic metabolism, rate of increase in blood lactate concentration for anaerobic lactic metabolism, rate of decrease in muscle phosphocreatine concentration for anaerobic alactic metabolism—and the rate of energy delivery (metabolic power) of each metabolism. The maximal powers and capacities and the corresponding energy equivalents, as reported by di Prampero (1981), are shown in Table 1.2.
for aerobic metabolism, rate of increase in blood lactate concentration for anaerobic lactic metabolism, rate of decrease in muscle phosphocreatine concentration for anaerobic alactic metabolism—and the rate of energy delivery (metabolic power) of each metabolism. The maximal powers and capacities and the corresponding energy equivalents, as reported by di Prampero (1981), are shown in Table 1.2.Table 1.2
Maximal capacity (Emax), maximal power (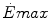 ) and time (t) at
) and time (t) at 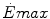 for the three energetic metabolisms, calculated for an ordinary human at 25 years of age
for the three energetic metabolisms, calculated for an ordinary human at 25 years of age
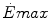 ) and time (t) at
) and time (t) at 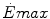 for the three energetic metabolisms, calculated for an ordinary human at 25 years of age
for the three energetic metabolisms, calculated for an ordinary human at 25 years of ageEmax (mmol kg−1) | 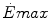 (μmol kg−1 s−1) (μmol kg−1 s−1) | 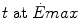 (s) (s) | |
|---|---|---|---|
Anaerobic alactic | 1.65 − 0.022 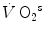 | 120 − 1.6 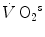 | 7.5 |
Anaerobic lactic | 2.5 | 56 | 44 |
Aerobic | 126 t − 0.132 t 2 | 37 | 56,400 – 1200 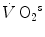 |