Stephen M Levin and Danièle-Claude Martin

Introduction

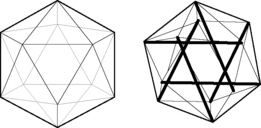
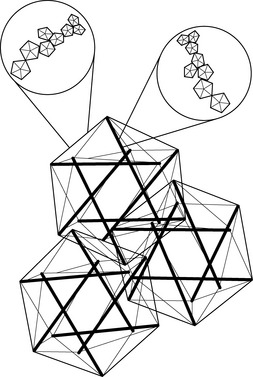
Fascia is the fabric of the body; not the vestments covering the corpus, but the warp and weft of the material. The other tissues, muscle and bone, liver and lung, gut and urinary, brain and endocrine, are embroidered into the fascial fabric. Remove all other tissues from their fascial bed and the structure and form of the corpus remains, ghostlike, but clearly defined. The fascial system is a continuum, a structure that evolved hierarchically from the one cell embryo to the organism, and it is constantly adapting to new stresses to meet the structural demands of the organism (Guimberteau et al. 2007). Fascia without stiffeners would be as limp as a rag doll; remove the hydroxyapatite crystals from bone, and the form of bones remains, but soft, as if the starch has been removed from a stiff shirt. Wolff recognized that bone is stiffened in response to compression stress and what must happen is that the support structure of the body, the fascia with its enmeshed bony stiffeners, evolves in accordance to physical laws (Wolff & Wessinghage 1892).

Fascia is a tension network, with all the collagen inherently stressed, the so-called “pre-stress” of biologic tissues. Where does the compression arise? It is easy to see in an archer’s bow. The bowstring pulls the limbs of the bow towards the center belly of the bow, compressing it, and bending the bow into its characteristic shape. Now imagine the “bow” being compressed toward its belly by multiple bowstrings that encircle the bow and are all pulled at once. If the forces were balanced, the bow would not bend, but merely compress. Tension elements at each end that compress toward the center can balance to create a pure compression force, and in a tensioned fascial network bone will be laid down, according to Wolff’s law.

The origins of biotensegrity

For this to happen, there must be some evolutionary structural process that is governed by the rules of physics and influenced by the genome. In 1981, a structural model was proposed that incorporated the physical laws related to triangulated (and therefore inherently stable) structural forms, “closest packing”, and foams, and the “tensegrity” structures as conceived by Kenneth Snelson (Snelson 2009) and Buckminster Fuller (Fuller & Applewhite 1975) into a biologic model that would appropriately model organisms from viruses to vertebrates, their systems and subsystems: biotensegrity (Levin 1981). Biotensegrity reverses the centuries-old concept that the skeleton is the frame upon which the soft tissue is draped, and replaces it with an integrated fascial fabric with “floating” compression elements (bones in vertebrates), enmeshed within the interstices of the tensioned elements.

For a structure to be stable with flexible joints, it must be triangulated, as only triangles are stable with flexible joints. Biologic structures, their elements joined by surface tension, and flexible soft tissues, must be triangulated structures for them to exist. If not triangulated, it would require stiff joints, or constant, unobtainable, muscle forces to keep from collapsing. Of the three fully triangulated structures, the tetrahedron, octahedron and icosahedron, the icosahedron is the most suitable for biologic modeling. It has the largest volume for surface area, is omnidirectional, has the closest packing capabilities, and endo- and exoskeletal configurations, where the compression elements are either in its outer shell, or incorporated into the innards of the structure (Fig. 3.5.1). The internally vectored icosahedron is a tensegrity structure, simply defined as “floating compression” elements enmeshed in a continuous tension network. The compression elements are isolated from one another and the load is carried through the network, and not a compression-loaded “column of blocks”, governed by gravity-oriented levers, as is the norm in most familiar structures. The tensegrity icosahedron can be linked in an infinite array, hierarchically and as fractals (Mandelbrot 1982; see Fig. 3.5.2). It is a low-energy structure, using minimal materials to enclose space and give maximum strength. Because of triangulation, it has flexible joints but is stable and adaptable. Its mechanics are nonlinear, which is consistent with biologic materials and structures. Columns depend on gravity to hold them together; without gravity, columns and structures that depend on columns for support would fall apart. Tensegrities are self-contained structures and do not rely on gravity as a cohesive force. Table 3.5.1 compares biologic structure properties with the properties of standard, lever mechanics and tensegrity icosahedral mechanics.

It is obvious that lever systems, the standard for over three centuries, do not match the qualities needed for biologic modeling, and tensegrity icosahedral systems are a perfect match.

Like coins crowded together on a tabletop, bubbles in foam, cells in a beehive, biologic cells must conform and adjust to the pressures surrounding them. The individual cell must keep from being crushed by external forces. From the standpoint of efficiency and conservation of energy, crowded objects on a two-dimensional plane will pack closest as hexagons. Three-dimensional cells will conform to what has been known about foams for over 100 years; they will pack closest with three edges meeting at 120° and four edges meeting at a corner. Icosahedrons will pack closest around a central, smaller, icosahedron, following these rules. Fuller has described the closest packing of icosahedrons as the closest relationship of energy efficient, symmetrical, stable structures in three dimensions (Fuller & Applewhite 1975). In the past, cells were thought of as bags of fluid and the incompressibility of fluid kept them from being crushed. In the early 1930s, an internal cell skeleton (the cytoskeleton) was suspected, but it took another two decades to demonstrate it using the electron microscope. Ingber proposed that the cytoskeleton is a tensegrity structure with a mechanical structural framework to support cell integrity and he models these tensegrities as icosahedrons (Ingber et al. 1981). Following Wolff’s law, the cytoskeleton will align itself in such a way as to resist the crushing compressive load, and the rigid tubulin of the cytoskeleton becomes its “bones”. Levin proposed that the same mechanism created a hierarchical evolution of the musculoskeletal system, a hierarchical tensegrity (Levin 1982, 1986, 1988, 1990). Kroto, the Nobel Prize winner for his work on C₆₀, the icosahedral form of carbon, demonstrates the self-organizing properties of icosahedrons into sphere-like structures and “icosaspirals”, helical structures of stacking icosahedrons (Kroto 1988). Icosahedrons and icosaspirals are ubiquitous in biologic structures, as demonstrated at every scale level: from 10⁻¹² m (e.g., the fullerene molecule C₆₀ and some amino acids) to 10⁻⁹ m (viruses, microtubules), to 10⁻⁶ m (red blood cells, pollen grains), to 10⁻⁴ m and 10⁻³ m (radiolarians), all the way up to organisms such as pufferfish at 10^− 2 m, and greater. This hierarchy of structure development results in a fascial continuum, from subcellular to total organism.