and the XYZ Euler angles  used to describe the end-effector orientation. It should be noted that both these quantities are observed in the global coordinate frame and are grouped together as the generalised coordinate vector given in (9.1).
used to describe the end-effector orientation. It should be noted that both these quantities are observed in the global coordinate frame and are grouped together as the generalised coordinate vector given in (9.1).
![$$ \xi = \left[ {\begin{array}{*{20}c} {x_{p} } \\ {\Theta } \\ \end{array}}\right] $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ1.gif)
(9.1)
Having decided on the generalised coordinates, the kinematic constraints imposed by the parallel mechanism can be established by observing the collocation of the 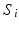 points. This means that the locations of the
points. This means that the locations of the 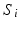 points as obtained from the task space generalised coordinates must be equivalent to those found using the actuating link coordinates. This relationship can be represented as (9.2), with
points as obtained from the task space generalised coordinates must be equivalent to those found using the actuating link coordinates. This relationship can be represented as (9.2), with 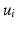 being a position vector describing the location of the universal joint
being a position vector describing the location of the universal joint 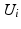 in the global frame. A mapping from the generalised coordinates
in the global frame. A mapping from the generalised coordinates 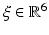 to three of the actuating link coordinates (
to three of the actuating link coordinates (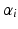 ,
, 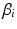 and
and 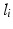 ) can therefore be obtained from (9.2). The time derivative of this relationship can then be used to obtain a Jacobian matrix
) can therefore be obtained from (9.2). The time derivative of this relationship can then be used to obtain a Jacobian matrix 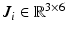 which relates the derivatives of the actuating link coordinates to the generalised coordinate derivatives as shown in (9.3).
which relates the derivatives of the actuating link coordinates to the generalised coordinate derivatives as shown in (9.3).
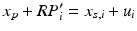
![$$ \left[ {\begin{array}{*{20}c} {\dot{\alpha }_{i} } \\ {\dot{\beta }_{i} } \\ {\dot{l}_{i} } \\ \end{array} } \right] = J_{i} \dot{\xi } $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ3.gif)
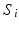 points. This means that the locations of the
points. This means that the locations of the 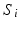 points as obtained from the task space generalised coordinates must be equivalent to those found using the actuating link coordinates. This relationship can be represented as (9.2), with
points as obtained from the task space generalised coordinates must be equivalent to those found using the actuating link coordinates. This relationship can be represented as (9.2), with 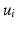 being a position vector describing the location of the universal joint
being a position vector describing the location of the universal joint 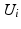 in the global frame. A mapping from the generalised coordinates
in the global frame. A mapping from the generalised coordinates 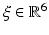 to three of the actuating link coordinates (
to three of the actuating link coordinates (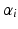 ,
, 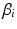 and
and 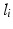 ) can therefore be obtained from (9.2). The time derivative of this relationship can then be used to obtain a Jacobian matrix
) can therefore be obtained from (9.2). The time derivative of this relationship can then be used to obtain a Jacobian matrix 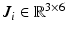 which relates the derivatives of the actuating link coordinates to the generalised coordinate derivatives as shown in (9.3).
which relates the derivatives of the actuating link coordinates to the generalised coordinate derivatives as shown in (9.3).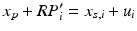
(9.2)
![$$ \left[ {\begin{array}{*{20}c} {\dot{\alpha }_{i} } \\ {\dot{\beta }_{i} } \\ {\dot{l}_{i} } \\ \end{array} } \right] = J_{i} \dot{\xi } $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ3.gif)
(9.3)
By considering the sensor deformations as additional state variables, the expressions for the centres of mass of the actuating link segments were represented in the general form given in (9.4), with 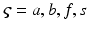 . Similarly, the angular velocities of the actuating links were also written in the form as given in (9.5). Repeated differentiation of (9.4) and (9.5) then leads to the actuating link acceleration terms being represented by
. Similarly, the angular velocities of the actuating links were also written in the form as given in (9.5). Repeated differentiation of (9.4) and (9.5) then leads to the actuating link acceleration terms being represented by 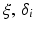 and their higher order time derivatives (up to the second order). With this in mind, the actuating link–end-effector interaction forces were restated as
and their higher order time derivatives (up to the second order). With this in mind, the actuating link–end-effector interaction forces were restated as 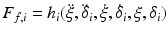 . It follows that the dynamic equations can be combined and viewed as (9.6), with
. It follows that the dynamic equations can be combined and viewed as (9.6), with ![$$ w_{\text{ext}} = \left[F_{\text{ext}}^{\text{T}} {M_{\text{ext}}^{\text{T}} } \right]^{\text{T}} \in {\mathbb{R}}^{6} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq15.gif) and
and ![$$ \delta = \left[ {\delta_{1} } {\delta_{2} } {\delta_{3} } {\delta_{4} } \right]^{\text{T}} \in {\mathbb{R}}^{4} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq16.gif) . Additionally,
. Additionally, 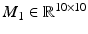 is the configuration-dependent matrix coefficient for the state acceleration variables,
is the configuration-dependent matrix coefficient for the state acceleration variables, 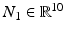 is the grouping of nonlinear terms, and
is the grouping of nonlinear terms, and 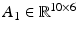 is the matrix coefficient for the external wrench applied to the end effector.
is the matrix coefficient for the external wrench applied to the end effector.
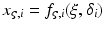
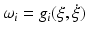
![$$ M_{1} \left( \xi \right)\left[ {\begin{array}{*{20}c} \ddot{\xi} \\ \ddot{\delta} \\ \end{array} } \right] + N_{1} \left( {\dot{\xi },\dot{\delta },\xi ,\delta } \right) + A_{1} \left( \xi \right)w_{\text{ext}} = 0 $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ6.gif)
 . Similarly, the angular velocities of the actuating links were also written in the form as given in (9.5). Repeated differentiation of (9.4) and (9.5) then leads to the actuating link acceleration terms being represented by
. Similarly, the angular velocities of the actuating links were also written in the form as given in (9.5). Repeated differentiation of (9.4) and (9.5) then leads to the actuating link acceleration terms being represented by 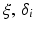 and their higher order time derivatives (up to the second order). With this in mind, the actuating link–end-effector interaction forces were restated as
and their higher order time derivatives (up to the second order). With this in mind, the actuating link–end-effector interaction forces were restated as 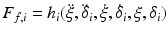 . It follows that the dynamic equations can be combined and viewed as (9.6), with
. It follows that the dynamic equations can be combined and viewed as (9.6), with ![$$ w_{\text{ext}} = \left[F_{\text{ext}}^{\text{T}} {M_{\text{ext}}^{\text{T}} } \right]^{\text{T}} \in {\mathbb{R}}^{6} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq15.gif) and
and ![$$ \delta = \left[ {\delta_{1} } {\delta_{2} } {\delta_{3} } {\delta_{4} } \right]^{\text{T}} \in {\mathbb{R}}^{4} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq16.gif) . Additionally,
. Additionally, 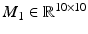 is the configuration-dependent matrix coefficient for the state acceleration variables,
is the configuration-dependent matrix coefficient for the state acceleration variables, 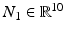 is the grouping of nonlinear terms, and
is the grouping of nonlinear terms, and 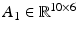 is the matrix coefficient for the external wrench applied to the end effector.
is the matrix coefficient for the external wrench applied to the end effector.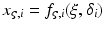
(9.4)
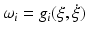
(9.5)
![$$ M_{1} \left( \xi \right)\left[ {\begin{array}{*{20}c} \ddot{\xi} \\ \ddot{\delta} \\ \end{array} } \right] + N_{1} \left( {\dot{\xi },\dot{\delta },\xi ,\delta } \right) + A_{1} \left( \xi \right)w_{\text{ext}} = 0 $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ6.gif)
(9.6)
Even with the reparameterisation, there are still only six equations available from (9.6), while there are ten unknown accelerations. Additional equations are therefore required to obtain a definite solution to the mechanism dynamics. Appending these equations to (9.6) will then lead to the complete model of the mechanism dynamics shown in (9.7), with ![$$ \begin{array}{*{20}c} {F_{\text{act}} = \left[ {F_{{{\text{act}},1}} F_{{{\text{act}},2}} F_{{{\text{act}},3}} F_{{{\text{act}},4}} } \right]^{\text{T}} } \\ \end{array} ,M \in {\mathbb{R}}^{10 \times 10} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq20.gif) being the matrix coefficient of the acceleration terms,
being the matrix coefficient of the acceleration terms, 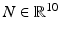 being the nonlinear dynamic terms,
being the nonlinear dynamic terms, 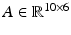 being the matrix coefficient for the interaction wrench and
being the matrix coefficient for the interaction wrench and 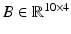 being the matrix coefficient for the actuator force vector.
being the matrix coefficient for the actuator force vector.
![$$ M \left( \xi \right) \left[ {\begin{array}{*{20}c} \ddot{\xi} \\ \ddot{\delta} \\ \end{array} } \right] + N\left( {\dot{\xi },\dot{\delta },\xi, \delta } \right) + A\left( \xi \right) w_{\text{ext}} = B\left( \xi \right) F_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ7.gif)
![$$ \begin{array}{*{20}c} {F_{\text{act}} = \left[ {F_{{{\text{act}},1}} F_{{{\text{act}},2}} F_{{{\text{act}},3}} F_{{{\text{act}},4}} } \right]^{\text{T}} } \\ \end{array} ,M \in {\mathbb{R}}^{10 \times 10} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq20.gif) being the matrix coefficient of the acceleration terms,
being the matrix coefficient of the acceleration terms, 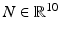 being the nonlinear dynamic terms,
being the nonlinear dynamic terms, 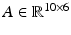 being the matrix coefficient for the interaction wrench and
being the matrix coefficient for the interaction wrench and 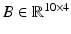 being the matrix coefficient for the actuator force vector.
being the matrix coefficient for the actuator force vector.![$$ M \left( \xi \right) \left[ {\begin{array}{*{20}c} \ddot{\xi} \\ \ddot{\delta} \\ \end{array} } \right] + N\left( {\dot{\xi },\dot{\delta },\xi, \delta } \right) + A\left( \xi \right) w_{\text{ext}} = B\left( \xi \right) F_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ7.gif)
(9.7)
9.1.2 Integration of Model with Foot and Actuator Dynamics
The integration of the foot model and the mechanism model can be done by first ensuring that the interaction ports on the foot and on the end effector are collocated. If this criterion in satisfied, the wrenches acting on the interaction port of the end effector will simply be equal but opposite of that acting on the foot model. This condition can therefore be used to combine the two models. In addition to the above condition, the kinematic relationship between generalised coordinates of the ankle model and the generalised coordinates of the end effector must also be found to allow further reparameterisation of the combined dynamic equations to yield a compact state space model which can be solved exactly. Clearly, as ankle model introduces additional kinematic constraints on the end effector, the final generalised coordinate would involve the ankle and subtalar joint displacements.
It can be seen that the ankle model can be represented in the form shown in (9.8), where 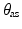 is the ankle and subtalar joint displacement,
is the ankle and subtalar joint displacement, 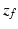 is a vector of additional state variables of the ankle model (which includes ligament and muscle–tendon states),
is a vector of additional state variables of the ankle model (which includes ligament and muscle–tendon states), 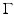 is a vector of muscle activation levels, and
is a vector of muscle activation levels, and 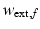 is the external wrench applied to the interaction port of the foot. Note also that the subscript
is the external wrench applied to the interaction port of the foot. Note also that the subscript 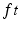 is used to denote the matrix coefficients and nonlinear dynamic terms relating to the ankle model, with
is used to denote the matrix coefficients and nonlinear dynamic terms relating to the ankle model, with 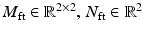 and
and 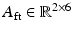 .
.
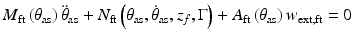
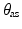 is the ankle and subtalar joint displacement,
is the ankle and subtalar joint displacement, 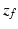 is a vector of additional state variables of the ankle model (which includes ligament and muscle–tendon states),
is a vector of additional state variables of the ankle model (which includes ligament and muscle–tendon states), 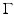 is a vector of muscle activation levels, and
is a vector of muscle activation levels, and 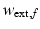 is the external wrench applied to the interaction port of the foot. Note also that the subscript
is the external wrench applied to the interaction port of the foot. Note also that the subscript 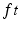 is used to denote the matrix coefficients and nonlinear dynamic terms relating to the ankle model, with
is used to denote the matrix coefficients and nonlinear dynamic terms relating to the ankle model, with 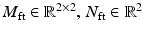 and
and 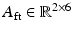 .
.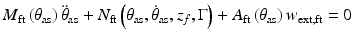
(9.8)
The kinematic relationship between 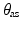 and
and 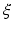 can be easily defined using the ankle kinematic model as long as the relative position of the end-effector centre of mass with respect to the subtalar joint centre is known at the neutral position of the ankle (by definition, this should also correspond to the end-effector orientation with zero XYZ Euler angles). This relationship was represented as (9.9) and was further differentiated with respect to time to give (9.10) and (9.11).
can be easily defined using the ankle kinematic model as long as the relative position of the end-effector centre of mass with respect to the subtalar joint centre is known at the neutral position of the ankle (by definition, this should also correspond to the end-effector orientation with zero XYZ Euler angles). This relationship was represented as (9.9) and was further differentiated with respect to time to give (9.10) and (9.11).
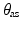 and
and 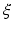 can be easily defined using the ankle kinematic model as long as the relative position of the end-effector centre of mass with respect to the subtalar joint centre is known at the neutral position of the ankle (by definition, this should also correspond to the end-effector orientation with zero XYZ Euler angles). This relationship was represented as (9.9) and was further differentiated with respect to time to give (9.10) and (9.11).
can be easily defined using the ankle kinematic model as long as the relative position of the end-effector centre of mass with respect to the subtalar joint centre is known at the neutral position of the ankle (by definition, this should also correspond to the end-effector orientation with zero XYZ Euler angles). This relationship was represented as (9.9) and was further differentiated with respect to time to give (9.10) and (9.11).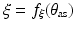
(9.9)
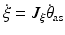
(9.10)
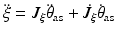
(9.11)
Equation (9.12) was reparameterised with 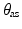 and its time derivatives. Note that the matrix coefficient of the acceleration terms (
and its time derivatives. Note that the matrix coefficient of the acceleration terms (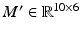 ) and nonlinear dynamic terms (
) and nonlinear dynamic terms (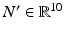 ) is different due to the substitution of the task space acceleration vector in (9.12).
) is different due to the substitution of the task space acceleration vector in (9.12).
![$$ M^{\prime} \left( {\theta_{\text{as}} } \right) \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}} } \\ \ddot{\delta} \\ \end{array} } \right] + N^{\prime} \left( {\dot{\theta }_{\text{as}} ,\dot{\delta }, \theta_{\text{as}} ,\delta } \right) + A\left( {\theta_{\text{as}} } \right) w_{\text{ext}} = B\left( {\theta_{\text{as}} } \right) F_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ12.gif)
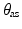 and its time derivatives. Note that the matrix coefficient of the acceleration terms (
and its time derivatives. Note that the matrix coefficient of the acceleration terms (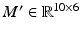 ) and nonlinear dynamic terms (
) and nonlinear dynamic terms (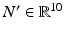 ) is different due to the substitution of the task space acceleration vector in (9.12).
) is different due to the substitution of the task space acceleration vector in (9.12).![$$ M^{\prime} \left( {\theta_{\text{as}} } \right) \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}} } \\ \ddot{\delta} \\ \end{array} } \right] + N^{\prime} \left( {\dot{\theta }_{\text{as}} ,\dot{\delta }, \theta_{\text{as}} ,\delta } \right) + A\left( {\theta_{\text{as}} } \right) w_{\text{ext}} = B\left( {\theta_{\text{as}} } \right) F_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ12.gif)
(9.12)
By recognising that 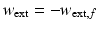 can be rewritten as (9.13). Note that the dependencies of the nonlinear terms and matrix coefficients will be dropped hereafter for brevity. It can be seen that pre-multiplication of (9.13) by
can be rewritten as (9.13). Note that the dependencies of the nonlinear terms and matrix coefficients will be dropped hereafter for brevity. It can be seen that pre-multiplication of (9.13) by 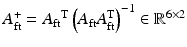 will result in (9.14), with
will result in (9.14), with 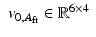 being the null space matrix of
being the null space matrix of 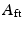 (with the null vectors occupying the columns of
(with the null vectors occupying the columns of 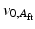 ). Equation (9.14) was then further expanded as (9.15), which showed that the actual interaction wrench can be represented by the summation of the right-hand side of (9.14) with an additional four degree of freedom vector
). Equation (9.14) was then further expanded as (9.15), which showed that the actual interaction wrench can be represented by the summation of the right-hand side of (9.14) with an additional four degree of freedom vector 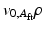 , with
, with 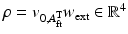 . Substituting this result into (9.12) then yields (9.16).
. Substituting this result into (9.12) then yields (9.16).
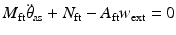
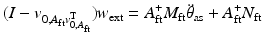
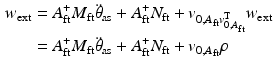
![$$ M^{\prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}} } \\ \ddot{\delta} \\ \end{array} } \right] + N^{\prime } + AA_{\text{ft}}^{ + } M_{\text{ft}} \ddot{\theta}_{\text{as}} + AA_{\text{ft}}^{ + } N_{\text{ft}} + Av_{{0, A_{\text{ft}} }} \rho = BF_{\text{act}} \Rightarrow M^{\prime \prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N^{\prime} + AA_{ft}^{ + } N_{\text{ft}} + Av_{{0, A_{\text{ft}} }} \rho = BF_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ16.gif)
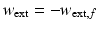 can be rewritten as (9.13). Note that the dependencies of the nonlinear terms and matrix coefficients will be dropped hereafter for brevity. It can be seen that pre-multiplication of (9.13) by
can be rewritten as (9.13). Note that the dependencies of the nonlinear terms and matrix coefficients will be dropped hereafter for brevity. It can be seen that pre-multiplication of (9.13) by 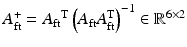 will result in (9.14), with
will result in (9.14), with 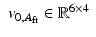 being the null space matrix of
being the null space matrix of 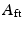 (with the null vectors occupying the columns of
(with the null vectors occupying the columns of 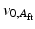 ). Equation (9.14) was then further expanded as (9.15), which showed that the actual interaction wrench can be represented by the summation of the right-hand side of (9.14) with an additional four degree of freedom vector
). Equation (9.14) was then further expanded as (9.15), which showed that the actual interaction wrench can be represented by the summation of the right-hand side of (9.14) with an additional four degree of freedom vector 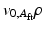 , with
, with 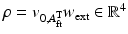 . Substituting this result into (9.12) then yields (9.16).
. Substituting this result into (9.12) then yields (9.16).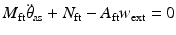
(9.13)
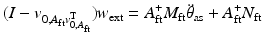
(9.14)
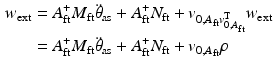
(9.15)
![$$ M^{\prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}} } \\ \ddot{\delta} \\ \end{array} } \right] + N^{\prime } + AA_{\text{ft}}^{ + } M_{\text{ft}} \ddot{\theta}_{\text{as}} + AA_{\text{ft}}^{ + } N_{\text{ft}} + Av_{{0, A_{\text{ft}} }} \rho = BF_{\text{act}} \Rightarrow M^{\prime \prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N^{\prime} + AA_{ft}^{ + } N_{\text{ft}} + Av_{{0, A_{\text{ft}} }} \rho = BF_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ16.gif)
(9.16)
Since the solution of 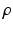 is of no interest, (9.16) was further pre-multiplied by
is of no interest, (9.16) was further pre-multiplied by ![$$ N_{A} = \left[ {\text{Null}\left( { v_{{0,A_{{{\text{ft}}}}^{{\text{T}}} }} A^{\text{T}} } \right)} \right]^{\text{T}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq44.gif) to yield (9.17), where the function
to yield (9.17), where the function 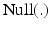 returns a matrix which columns are filled by the null vectors of the function argument (i.e.
returns a matrix which columns are filled by the null vectors of the function argument (i.e. 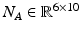 ). Inspection of (9.17) reveals that there are now six acceleration variables and six equations, which means that the acceleration variables can be solved exactly given certain actuator forces and muscle activation levels. Clearly, the state space model of the foot-manipulator system will only be complete when the state transition equations for the ligament and muscle–tendon states are included.
). Inspection of (9.17) reveals that there are now six acceleration variables and six equations, which means that the acceleration variables can be solved exactly given certain actuator forces and muscle activation levels. Clearly, the state space model of the foot-manipulator system will only be complete when the state transition equations for the ligament and muscle–tendon states are included.
![$$ N_{A} M^{\prime \prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N_{A} N^{\prime} + N_{A} AA_{{\text{ft}}^{ + }} N_{\text{ft}} = N_{A} BF_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ17.gif)
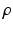 is of no interest, (9.16) was further pre-multiplied by
is of no interest, (9.16) was further pre-multiplied by ![$$ N_{A} = \left[ {\text{Null}\left( { v_{{0,A_{{{\text{ft}}}}^{{\text{T}}} }} A^{\text{T}} } \right)} \right]^{\text{T}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_IEq44.gif) to yield (9.17), where the function
to yield (9.17), where the function 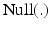 returns a matrix which columns are filled by the null vectors of the function argument (i.e.
returns a matrix which columns are filled by the null vectors of the function argument (i.e. 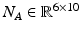 ). Inspection of (9.17) reveals that there are now six acceleration variables and six equations, which means that the acceleration variables can be solved exactly given certain actuator forces and muscle activation levels. Clearly, the state space model of the foot-manipulator system will only be complete when the state transition equations for the ligament and muscle–tendon states are included.
). Inspection of (9.17) reveals that there are now six acceleration variables and six equations, which means that the acceleration variables can be solved exactly given certain actuator forces and muscle activation levels. Clearly, the state space model of the foot-manipulator system will only be complete when the state transition equations for the ligament and muscle–tendon states are included.![$$ N_{A} M^{\prime \prime } \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N_{A} N^{\prime} + N_{A} AA_{{\text{ft}}^{ + }} N_{\text{ft}} = N_{A} BF_{\text{act}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ17.gif)
(9.17)
Based on the actuating link coordinates, the actuator dynamics was expressed as (9.18), with 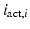 being the actuator current,
being the actuator current, 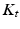 being the motor torque constant,
being the motor torque constant, 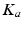 being the actuator transmission ratio,
being the actuator transmission ratio,  being the effective motor inertia,
being the effective motor inertia, 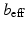 being the effective viscous damping of the motor and
being the effective viscous damping of the motor and 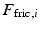 being the Coulomb friction experienced by the actuator. Since
being the Coulomb friction experienced by the actuator. Since 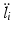 and
and 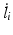 can ultimately be related to the accelerations and velocities of the ankle and subtalar joints, (9.18) was reorganised as (9.19). Substitution of (9.19) into (9.17) will then lead to the set of equations which describes the rigid body dynamics of the actuator, parallel mechanism and foot. This set of equations is given in (9.20), with
can ultimately be related to the accelerations and velocities of the ankle and subtalar joints, (9.18) was reorganised as (9.19). Substitution of (9.19) into (9.17) will then lead to the set of equations which describes the rigid body dynamics of the actuator, parallel mechanism and foot. This set of equations is given in (9.20), with 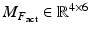 being a matrix which rows are consisted of
being a matrix which rows are consisted of 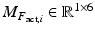 and
and 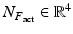 being a vector which rows are consisted of
being a vector which rows are consisted of 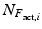 .
.
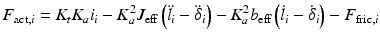
![$$ F_{\text{act},i} = K_{t} K_{a} i_{\text{act,i}} - M_{{F_{\text{act},i} }} \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] - N_{{F_{\text{act,i}} }} - F_{\text{fric},i} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ19.gif)
![$$ \begin{aligned} & \left( {N_{A} M^{\prime \prime } + N_{A} BM_{{F_{\text{act}} }} } \right)\left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N_{A} N^{\prime } + N_{A} BN_{{F_{\text{act}} }} + N_{A} BF_{\text{fric}} \\ & \quad\quad + N_{A} AA_{\text{ft}}^{ + } N_{\text{ft}} = K_{t} K_{a} N_{A} Bi_{\text{act}} \\ \end{aligned} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ20.gif)
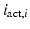 being the actuator current,
being the actuator current, 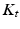 being the motor torque constant,
being the motor torque constant, 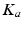 being the actuator transmission ratio,
being the actuator transmission ratio,  being the effective motor inertia,
being the effective motor inertia, 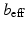 being the effective viscous damping of the motor and
being the effective viscous damping of the motor and 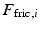 being the Coulomb friction experienced by the actuator. Since
being the Coulomb friction experienced by the actuator. Since 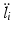 and
and 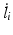 can ultimately be related to the accelerations and velocities of the ankle and subtalar joints, (9.18) was reorganised as (9.19). Substitution of (9.19) into (9.17) will then lead to the set of equations which describes the rigid body dynamics of the actuator, parallel mechanism and foot. This set of equations is given in (9.20), with
can ultimately be related to the accelerations and velocities of the ankle and subtalar joints, (9.18) was reorganised as (9.19). Substitution of (9.19) into (9.17) will then lead to the set of equations which describes the rigid body dynamics of the actuator, parallel mechanism and foot. This set of equations is given in (9.20), with 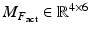 being a matrix which rows are consisted of
being a matrix which rows are consisted of 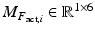 and
and 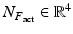 being a vector which rows are consisted of
being a vector which rows are consisted of 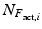 .
.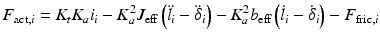
(9.18)
![$$ F_{\text{act},i} = K_{t} K_{a} i_{\text{act,i}} - M_{{F_{\text{act},i} }} \left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] - N_{{F_{\text{act,i}} }} - F_{\text{fric},i} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ19.gif)
(9.19)
![$$ \begin{aligned} & \left( {N_{A} M^{\prime \prime } + N_{A} BM_{{F_{\text{act}} }} } \right)\left[ {\begin{array}{*{20}c} {\ddot{\theta}_{\text{as}}} \\ \ddot{\delta}\\ \end{array} } \right] + N_{A} N^{\prime } + N_{A} BN_{{F_{\text{act}} }} + N_{A} BF_{\text{fric}} \\ & \quad\quad + N_{A} AA_{\text{ft}}^{ + } N_{\text{ft}} = K_{t} K_{a} N_{A} Bi_{\text{act}} \\ \end{aligned} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ20.gif)
(9.20)
9.1.3 Elementary Robot Control
In the context of rehabilitation robots, the force variable is the user–robot interaction force, while the motion variable is simply the movement of the joint or limb under rehabilitation. It should also be noted that the dynamic relationships described above are typically represented as a second-order mechanical system as shown in (9.21) with inertial (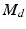 ), damping (
), damping (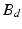 ) and stiffness (
) and stiffness (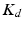 ) parameters. Additionally, the variables
) parameters. Additionally, the variables 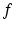 ,
, 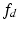 ,
, 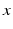 and
and 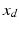 are, respectively, used to denote the force applied to the environment, the desired force, the actual position of the end effector and the desired end-effector position. The advantage of having the force and motion variables in relative terms is that it allows variation in the equilibrium position about which the impedance relationship is based, thus allowing the use of this control strategy for a wider range of tasks. In fact, when put in this form, pure motion control and pure force control can simply be viewed as special cases of impedance control, where pure motion control can be achieved with infinitely large impedance and pure force control with zero impedance. Due to its versatility, the interaction control scheme developed for the ankle rehabilitation robot is based on this general impedance control law.
are, respectively, used to denote the force applied to the environment, the desired force, the actual position of the end effector and the desired end-effector position. The advantage of having the force and motion variables in relative terms is that it allows variation in the equilibrium position about which the impedance relationship is based, thus allowing the use of this control strategy for a wider range of tasks. In fact, when put in this form, pure motion control and pure force control can simply be viewed as special cases of impedance control, where pure motion control can be achieved with infinitely large impedance and pure force control with zero impedance. Due to its versatility, the interaction control scheme developed for the ankle rehabilitation robot is based on this general impedance control law.
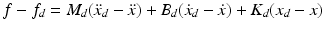
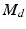 ), damping (
), damping (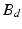 ) and stiffness (
) and stiffness (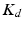 ) parameters. Additionally, the variables
) parameters. Additionally, the variables 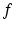 ,
, 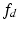 ,
, 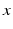 and
and 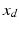 are, respectively, used to denote the force applied to the environment, the desired force, the actual position of the end effector and the desired end-effector position. The advantage of having the force and motion variables in relative terms is that it allows variation in the equilibrium position about which the impedance relationship is based, thus allowing the use of this control strategy for a wider range of tasks. In fact, when put in this form, pure motion control and pure force control can simply be viewed as special cases of impedance control, where pure motion control can be achieved with infinitely large impedance and pure force control with zero impedance. Due to its versatility, the interaction control scheme developed for the ankle rehabilitation robot is based on this general impedance control law.
are, respectively, used to denote the force applied to the environment, the desired force, the actual position of the end effector and the desired end-effector position. The advantage of having the force and motion variables in relative terms is that it allows variation in the equilibrium position about which the impedance relationship is based, thus allowing the use of this control strategy for a wider range of tasks. In fact, when put in this form, pure motion control and pure force control can simply be viewed as special cases of impedance control, where pure motion control can be achieved with infinitely large impedance and pure force control with zero impedance. Due to its versatility, the interaction control scheme developed for the ankle rehabilitation robot is based on this general impedance control law.
(9.21)
It is easy to see that implementation of the impedance control law can be done by issuing 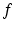 as a force command to the actuator force controller. This means that an outer motion control loop is required to complete the impedance control scheme. Since the actuator force controller is defined in joint space while the impedance control law is applied in task space to allow more intuitive description of the desired manipulator behaviour, the actual input to the outer impedance loop would be the motion variables in terms of end-effector orientation and the output will be that of the torques along the task space coordinates. This torque must therefore be transformed into their corresponding actuator forces prior to it being used as force commands for the inner force control loop. In order to derive this force command, it is necessary to first consider the desired impedance relationship in task space as shown in (9.22), where
as a force command to the actuator force controller. This means that an outer motion control loop is required to complete the impedance control scheme. Since the actuator force controller is defined in joint space while the impedance control law is applied in task space to allow more intuitive description of the desired manipulator behaviour, the actual input to the outer impedance loop would be the motion variables in terms of end-effector orientation and the output will be that of the torques along the task space coordinates. This torque must therefore be transformed into their corresponding actuator forces prior to it being used as force commands for the inner force control loop. In order to derive this force command, it is necessary to first consider the desired impedance relationship in task space as shown in (9.22), where  is the robot–user interaction torque,
is the robot–user interaction torque, 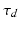 is the desired interaction torque,
is the desired interaction torque, 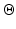 is the task space coordinates in XYZ Euler angles, and
is the task space coordinates in XYZ Euler angles, and 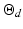 is the desired task space position. Note that the desired task space acceleration is deliberately left off the inertial component of the impedance relationship to simplify the control law. As the main focus of the impedance control law is not to achieve pure position control, this simplification is acceptable.
is the desired task space position. Note that the desired task space acceleration is deliberately left off the inertial component of the impedance relationship to simplify the control law. As the main focus of the impedance control law is not to achieve pure position control, this simplification is acceptable.
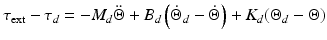
 as a force command to the actuator force controller. This means that an outer motion control loop is required to complete the impedance control scheme. Since the actuator force controller is defined in joint space while the impedance control law is applied in task space to allow more intuitive description of the desired manipulator behaviour, the actual input to the outer impedance loop would be the motion variables in terms of end-effector orientation and the output will be that of the torques along the task space coordinates. This torque must therefore be transformed into their corresponding actuator forces prior to it being used as force commands for the inner force control loop. In order to derive this force command, it is necessary to first consider the desired impedance relationship in task space as shown in (9.22), where
as a force command to the actuator force controller. This means that an outer motion control loop is required to complete the impedance control scheme. Since the actuator force controller is defined in joint space while the impedance control law is applied in task space to allow more intuitive description of the desired manipulator behaviour, the actual input to the outer impedance loop would be the motion variables in terms of end-effector orientation and the output will be that of the torques along the task space coordinates. This torque must therefore be transformed into their corresponding actuator forces prior to it being used as force commands for the inner force control loop. In order to derive this force command, it is necessary to first consider the desired impedance relationship in task space as shown in (9.22), where  is the robot–user interaction torque,
is the robot–user interaction torque, 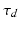 is the desired interaction torque,
is the desired interaction torque, 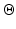 is the task space coordinates in XYZ Euler angles, and
is the task space coordinates in XYZ Euler angles, and 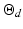 is the desired task space position. Note that the desired task space acceleration is deliberately left off the inertial component of the impedance relationship to simplify the control law. As the main focus of the impedance control law is not to achieve pure position control, this simplification is acceptable.
is the desired task space position. Note that the desired task space acceleration is deliberately left off the inertial component of the impedance relationship to simplify the control law. As the main focus of the impedance control law is not to achieve pure position control, this simplification is acceptable.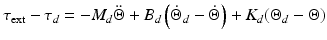
(9.22)
By considering the influence of the inner actuator force control law, the effective dynamics of the manipulator can be rewritten as (9.23), where 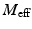 is the effective inertia matrix and
is the effective inertia matrix and 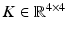 is the gain matrix used in the inner force controller. Also,
is the gain matrix used in the inner force controller. Also, 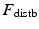 is used to refer to the actuator disturbance forces,
is used to refer to the actuator disturbance forces, 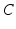 is used to represent the centripetal and Coriolis forces in the manipulator dynamics, and
is used to represent the centripetal and Coriolis forces in the manipulator dynamics, and 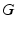 is used to represent the gravitational forces in the manipulator dynamics. Finally,
is used to represent the gravitational forces in the manipulator dynamics. Finally, 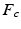 represents the force command issued to the inner force controller. By considering (9.22) and (9.23), as well as the fact that
represents the force command issued to the inner force controller. By considering (9.22) and (9.23), as well as the fact that 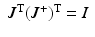 , a suitable impedance control law can be constructed. This is shown in (9.24). The dynamics of the impedance controlled manipulator (9.25) was then obtained.
, a suitable impedance control law can be constructed. This is shown in (9.24). The dynamics of the impedance controlled manipulator (9.25) was then obtained.
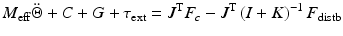
![$$ F_{c} = (J^{ + } )^{\text{T}} \left[ {\tau_{d} + B_{d} \left( {{\dot{\Theta }}}_{d} - {\dot{\Theta }} \right) + K_{d} \left( {{\Theta }_{d} - {\Theta }} \right) + C + G} \right] $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ24.gif)
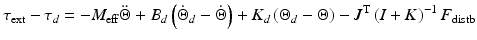
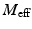 is the effective inertia matrix and
is the effective inertia matrix and 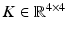 is the gain matrix used in the inner force controller. Also,
is the gain matrix used in the inner force controller. Also, 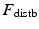 is used to refer to the actuator disturbance forces,
is used to refer to the actuator disturbance forces, 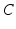 is used to represent the centripetal and Coriolis forces in the manipulator dynamics, and
is used to represent the centripetal and Coriolis forces in the manipulator dynamics, and 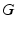 is used to represent the gravitational forces in the manipulator dynamics. Finally,
is used to represent the gravitational forces in the manipulator dynamics. Finally, 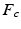 represents the force command issued to the inner force controller. By considering (9.22) and (9.23), as well as the fact that
represents the force command issued to the inner force controller. By considering (9.22) and (9.23), as well as the fact that 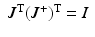 , a suitable impedance control law can be constructed. This is shown in (9.24). The dynamics of the impedance controlled manipulator (9.25) was then obtained.
, a suitable impedance control law can be constructed. This is shown in (9.24). The dynamics of the impedance controlled manipulator (9.25) was then obtained.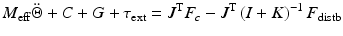
(9.23)
![$$ F_{c} = (J^{ + } )^{\text{T}} \left[ {\tau_{d} + B_{d} \left( {{\dot{\Theta }}}_{d} - {\dot{\Theta }} \right) + K_{d} \left( {{\Theta }_{d} - {\Theta }} \right) + C + G} \right] $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ24.gif)
(9.24)
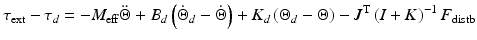
(9.25)
9.1.4 Simulation and Experimental Results
In order to evaluate the efficacy of the proposed elementary control scheme on the ankle rehabilitation robot, the developed impedance controller, the redundancy resolution scheme and an inner actuator force controller were all applied to the integrated foot–robot model presented earlier in this chapter. The simulation was carried out to emulate the scenario where the robot is used to guide the patient’s foot under impedance control along certain rehabilitation trajectory, while the user remains passive (i.e. no muscle activation). The trajectory used in the simulation was chosen to resemble pronation–supination motion of the foot and are given in (9.26), where the angles are expressed in radians and the variable 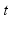 is the simulation time. The reference moment
is the simulation time. The reference moment 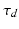 in the basic impedance control law was also set to be zero throughout the duration of the simulation.
in the basic impedance control law was also set to be zero throughout the duration of the simulation.
![$$ \left[ {\begin{array}{*{20}c} {\theta_{x} } & {\theta_{y} } & {\theta_{z} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} {\frac{\pi }{6}\sin \left( {\frac{\pi t}{6}} \right)} & {\frac{\pi }{9}\sin \left( {\frac{\pi t}{6}} \right)} & { - \frac{\pi }{12}\sin \left( {\frac{\pi t}{6}} \right)} \\ \end{array} } \right]^{\text{T}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ26.gif)
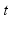 is the simulation time. The reference moment
is the simulation time. The reference moment 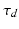 in the basic impedance control law was also set to be zero throughout the duration of the simulation.
in the basic impedance control law was also set to be zero throughout the duration of the simulation.![$$ \left[ {\begin{array}{*{20}c} {\theta_{x} } & {\theta_{y} } & {\theta_{z} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} {\frac{\pi }{6}\sin \left( {\frac{\pi t}{6}} \right)} & {\frac{\pi }{9}\sin \left( {\frac{\pi t}{6}} \right)} & { - \frac{\pi }{12}\sin \left( {\frac{\pi t}{6}} \right)} \\ \end{array} } \right]^{\text{T}} $$](/wp-content/uploads/2016/09/A313541_1_En_9_Chapter_Equ26.gif)
(9.26)
9.1.4.1 Simulation with Rigid Biaxial Ankle Kinematics
Preliminary simulations have shown that the actuator force controller cannot be applied directly to the integrated model without causing system instability. Investigation into the problem revealed that the gains used in the proposed gain scheduling force controller were too large. Further analysis showed that the cause for this problem lied in the fact that the ankle kinematic model used was of only two DOFs. The result of this is an altered manipulator Jacobian and hence also a variation in the decoupled directions and their associated singular values. Since the gain margin along the null vector was relatively low for the three DOF manipulator model used to formulate the proposed controller, direct application of the proposed force controller to a two DOF system had resulted in an unstable system. This is because the presence of an additional vector in the null space means that some of the higher gains applied in other directions will be projected onto the null vectors instead, thus increasing the effective gains beyond the critical gain and ultimately causing system instability. A similar phenomenon can also occur for the least stable decoupled direction in the two degree of freedom model due to the mismatch of assumed and actual decoupled directions.
The above notion is supported by the fact that system stability can be restored when the force controller is redesigned by taking into account the manipulator Jacobian and inertia matrix of the two DOF system. Using constant gains along the principal directions computed from the newly formulated coupling term, it was found that higher gains can be applied along directions with smaller singular values. Results of the simulation carried out using this modified inner force controller are given in Fig. 9.1. An isotropic robot stiffness of 10 Nm/rad and a robot damping of 2 Nms/rad were used in the simulation. Additionally, a desired vertical force of −150 N was also used in the redundancy resolution scheme.
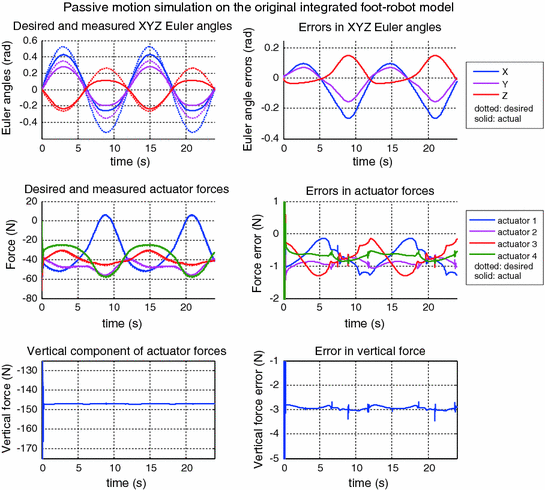

Fig. 9.1
Simulation results of a passive motion trial on the ankle rehabilitation robot. This simulation applies the proposed basic impedance controller, redundancy resolution scheme and a modified actuator force controller on the integrated foot–robot model
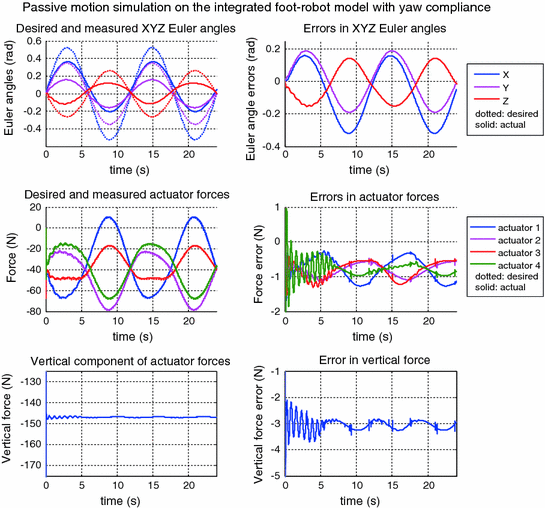
9.1.4.2 Simulation with Added Yaw Compliance
Based on the findings obtained from the above simulation, an important point which needs to be addressed is whether the proposed actuator force controller can be applied to the actual ankle rehabilitation robot. To represent this in the simulated system, an additional degree of freedom had been included in the ankle model through addition of an extra revolute joint at the talus. This revolute joint is fixed in the vertical (yaw) direction, and the talus was allowed to rotate about this joint. A set of linear rotational spring and damper units with reasonably large stiffness and damping (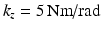 ,
, 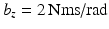 ) were also added along this joint. These parameters had been chosen manually to prevent large angular deflections about this axis while maintaining a well-damped system. It should be noted that due to added complexities in the kinematic structure of the integrated foot–robot system, there exists discrepancies between the inertia matrices to obtain the gain margins and the actual inertia matrices of the integrated system. Consequently, the gains of the proposed controller were reduced (to approximately 75 % of their original values) to ensure stability. The relative magnitudes of these gains, however, still followed the same trend as that used in the proposed controller. The results of this simulation are summarised in Fig. 9.2.
) were also added along this joint. These parameters had been chosen manually to prevent large angular deflections about this axis while maintaining a well-damped system. It should be noted that due to added complexities in the kinematic structure of the integrated foot–robot system, there exists discrepancies between the inertia matrices to obtain the gain margins and the actual inertia matrices of the integrated system. Consequently, the gains of the proposed controller were reduced (to approximately 75 % of their original values) to ensure stability. The relative magnitudes of these gains, however, still followed the same trend as that used in the proposed controller. The results of this simulation are summarised in Fig. 9.2.
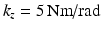 ,
, 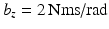 ) were also added along this joint. These parameters had been chosen manually to prevent large angular deflections about this axis while maintaining a well-damped system. It should be noted that due to added complexities in the kinematic structure of the integrated foot–robot system, there exists discrepancies between the inertia matrices to obtain the gain margins and the actual inertia matrices of the integrated system. Consequently, the gains of the proposed controller were reduced (to approximately 75 % of their original values) to ensure stability. The relative magnitudes of these gains, however, still followed the same trend as that used in the proposed controller. The results of this simulation are summarised in Fig. 9.2.
) were also added along this joint. These parameters had been chosen manually to prevent large angular deflections about this axis while maintaining a well-damped system. It should be noted that due to added complexities in the kinematic structure of the integrated foot–robot system, there exists discrepancies between the inertia matrices to obtain the gain margins and the actual inertia matrices of the integrated system. Consequently, the gains of the proposed controller were reduced (to approximately 75 % of their original values) to ensure stability. The relative magnitudes of these gains, however, still followed the same trend as that used in the proposed controller. The results of this simulation are summarised in Fig. 9.2.
Fig. 9.2
Simulation results of a passive motion trial on the ankle rehabilitation robot. This simulation applies the proposed basic impedance controller, redundancy resolution scheme and actuator force controller on the integrated foot–robot model with added yaw compliance
The results obtained from the simulation trials show a comparable level of force tracking capability in both systems. This, however, does not translate to a similar position following capability, with errors in the yaw compliant model much larger than that of the original foot–robot model. By noting that the same impedance controller has been used and that the force tracking capability in both systems are similar, the difference in the position errors must be caused by the addition of the yaw axis compliance. This is also believed to be partly the cause of the initial oscillations observed in the second simulation trial. Despite these differences, it is clear from both simulations that larger position errors can be found in the negative X-direction, an observation that is in line with greater ankle stiffness in the dorsiflexion direction. The simulation results also show that the redundancy resolution scheme is working well, with the total vertical force regulated to about 3 N of the desired set point in the absence of friction along the actuators.
9.1.4.3 Experimental Results
In addition to the simulations, the basic impedance controller was also tested experimentally using the actual ankle rehabilitation robot with a healthy test subject. The subject is an adult male (1.75 m height), and ethics approval had been granted by The University of Auckland Human Participants Ethics Committee (Ref. 2009/480). The foot of the user is attached onto the robot end-effector platform using Velcro strips, while the shank of the subject is attached through a shin guard to the shank brace on the ankle rehabilitation robot. The subject remained relaxed throughout the trial to minimise muscle activations, and thus, the resulting motion can be considered passive. A segment of the results obtained from this experiment is shown in Fig. 9.3. Note that the inner actuator force controller used in the experiment is that of the originally proposed force controller with no gain reduction as it was found to be stable in preliminary trials on the robot, and thus, higher gains were used to improve force tracking performance.
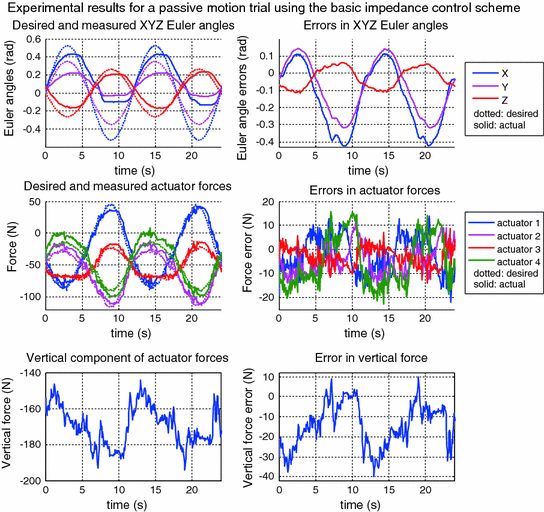

Fig. 9.3
Experimental results of a passive motion trial on the ankle rehabilitation robot. This simulation applies the proposed basic impedance controller, redundancy resolution scheme and actuator force controller on the actual ankle rehabilitation robot
It can be seen from the experimental results that the force tracking capability on the robot was worse than that observed in the simulation. This was expected since friction was not included in the integrated model. Focusing on the performance of the basic impedance control scheme, it can be seen that the errors in X Euler angle did follow a very similar trend to those obtained from simulations, again with much larger errors in the negative X Euler (or dorsiflexion) direction. The motion in the Y Euler angle direction, however, was rather different from those seen in simulations as there was hardly any movement in the negative y-direction. This can be due to several factors, one of which is the difference between the actual ankle stiffness and the stiffness of the ankle model used in simulation. Secondly, frictions within the actuators and passive robot joints can also contribute to smaller effective moments being applied to the foot. Lastly, imperfect attachment of the shank to the robot can also lead to the robot coordinate frame not being aligned perfectly with the ideal foot coordinate frame. The results, however, suggest that the first two factors could be more dominant here due to the small amount of negative y motion observed, while if the third factor is dominant, then there should only be some form of bias/offset in the trajectory. Motion along the Z Euler angle shows that the measured motion in the z-direction is actually tracking the desired trajectory quite closely compared to the simulations. This again can be due to discrepancies between the stiffness characteristics of the ankle model and the actual foot, or it can also be due to the fact that the yaw compliance is greater than assumed in the model used for the second simulation.
9.2 Adaptive Interaction Control via Variable Impedance
9.2.1 Biomechanical Model-Based Impedance Adjustment
The robot impedance also need not be held constant during robot operation. In fact, researchers had developed more advanced impedance control schemes which vary the robot impedance parameters according to the environmental characteristics [1] or to the task being carried out [2]. An example of the above in the area of physical human–robot interaction includes the variation of robot damping during human–robot cooperative tasks to improve coupled stability [3].
Clearly, knowledge of the environmental admittance is essential to allow implementation of the adopted impedance selection rule. This information can be estimated by considering the computational ankle model. Since the robot is expected to operate in low velocity conditions, only the steady-state behaviour of the ankle model was used to estimate the environmental characteristics. This means that only the stiffness/compliance of the environment is observed in the development of this impedance adaptation scheme. Additionally, the environmental characteristics were also obtained in the absence of any muscular activation, or in other words, when the foot is completely passive.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








