, Ardiyansyah Syahrom2 , Muhamad Noor Harun2 and Mohammed Rafiq Abdul Kadir3
(1)
Department of Applied Solid Mechanics and Design, Universiti Teknologi Malaysia, Johor, Malaysia
(2)
Sport Innovation and Technology Centre (SITC), Universiti Teknologi Malaysia, Johor, Malaysia
(3)
Faculty of Biosciences and Medical Engineering, Department of Clinical Sciences, Universiti Teknologi Malaysia, Johor, Malaysia
Abstract
Computational wear simulation of TAR were developed using the Archard’s wear model. Wear rate is the ultimate performance indicator of wear. The parameter such as ankle joint loading and kinematics were used in determining wear rates. Historically, wear performance was assessed by experimental means of clinical and physical simulators. Therefore, this present studies was used the finite element method to predict wear of TAR with adaptive re-meshing technique. The wear sensitivity test was conducted to determine the wear update interval and converge at 0.5 million cycles for update interval.
Keywords
WearWear sensitivityArchard’s wear modelAdaptive re-meshingUpdate interval3.1 Fundamental of Wear Modelling
Wear always refers to the process of removing material from solid surfaces by mechanical action. Wear can happen in many ways, depending on the material used for the interacting contact surfaces, the operating environment, and the running conditions. In engineering terms, wear is usually categorized as either mild or severe. Mild and severe wear are determined by the operating conditions, but different types of wear can be recognized by referring to the fundamental wear mechanisms involved, such as adhesive wear, abrasive wear, corrosive wear, and surface fatigue wear.
Archard developed the earliest theory of wear model in 1953 whereby the theory described sliding wear. The Archard wear law was primarily derived for rough metallic bearing surfaces. The theoretical assumption was made where the asperities were deformed plastically so that the real contact area was directly proportional to the load applied [1]. The Archard wear equation model was given by Archard [2]:
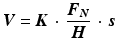
where V is the wear volume, K is the dimensionless wear coefficient F N , is the normal load, H is the hardness of the soft contact surface and s is the sliding distance. Often, Eq. 3.1 is more conveniently written by dividing both sides by the contact area A and by replacing K/H with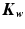 
:
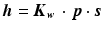
where h is the wear depth in m, Kw, is wear factor in m2/N, p is the contact pressure in Pa, and s is the sliding distance in m. The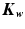 
-value is given in m3/Nm or m2/N, sometimes in mm3/Nm. The 
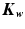-value just like the friction coefficient, depends on a lot of parameters and this factor is to be found experimentally [3]. Wear rates are determined by dividing the number of cycle of joint activities per year [4].
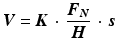
(3.1)
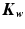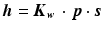
:(3.2)
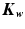-value is given in m3/Nm or m2/N, sometimes in mm3/Nm. The 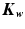-value just like the friction coefficient, depends on a lot of parameters and this factor is to be found experimentally [3]. Wear rates are determined by dividing the number of cycle of joint activities per year [4].In most cases, wear is assumed to concentrate in the polyethylene component UHMWPE, which is softer than the metallic component of the talar and tibial component. In addition, during in vivo activity, several wear mechanisms such as fatigue and corrosive wear could affect the implant. However, only abrasion and adhesion were considered [5]. Furthermore, the articular contact surface was considered as a dry contact while the lubrication effect was including in the wear factor Kw.
The value of the wear factor for the total ankle replacement was not established either in modelling or in vitro simulation studies. As mentioned before, the wear studied on total ankle replacement was far behind compared to total knee replacement and total hip replacement. Although the standard wear simulator protocol was widely developed and implemented for knee and hip replacement, there were no specialized simulators for the human ankle joint. It was also found that there was no standard protocol for wear simulator of total ankle replacement. The wear simulation study of total ankle replacement was performed using knee simulator [6, 7]. The value of wear factor obtained using total knee replacement and ball on flat wear test was 2.64E-07 mm3/Nm [8, 9].
3.1.1 Wear of Total Ankle Replacement (TAR)
Several factors contributed to the wear of joint replacement. Some parameters such as surface finish, material pairing, and conformity would be the main cause for production of wear. Thus, that explains the necessity to control these parameters. Meanwhile other parameters that were based on the patients, such as loading and kinematic were determined. However, the ultimate performance indicator of wear was identified by the wear rate. The wear rate plays a major role in wear performance. Other parameters that can affect the performance of wear are contact area and contact pressure in wear predictions.
Although diverse studies on implant designs and anatomical sites such as hips, knees and ankle joints have specific considerations, a common issue pre-clinically is the necessity to reliably estimate in vivo or in vitro studies of wear performance. Historically, both clinical and laboratory studies have been the primary options in measuring the wear of the implants to assess their performance [7, 10–13]. Physical simulators have expanded to incorporate most of the major factors thought to influence wear [14, 15]. However, these in vivo or in vitro study equipment involved are costly and time-consuming, while a comprehensive understanding on the aspect of design parameters was needed and even the ability to address novel influence factors is limited.
Finite element method (FEM) is a powerful computational tool that has been widely used to improvise the design of joint prostheses and to minimise the costly experimental trials. A lot of studies have been conducted, using the FEM, to understand the contact stresses, deformation, damage and failure of the prostheses [15, 16]. Wear simulations using computational method have come into increasing usage. An early efforts of the use of computational method on biomechanics was on application of total hips replacement (THR), pioneered by Maxian et al. [4] who implemented the classic Archard/Lancaster relationship [2]. The extensions of that formulation are widely used on other joints except for the ankle joint [4, 9, 17, 18]. Wear simulation on the application of total ankle replacement (TAR) was tested in vitro using simulators. Table 3.1 shows several wear testing using simulators.
Table 3.1
Wear rate for selected TAR
Source | Implants | Cycles (Million) | Wear rate (mm3/Million cycles (Mc)) |
|---|---|---|---|
Bell et al. (2007) [7] | BP | 5
Related posts: Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
Get Clinical Tree app for offline access
|
