Vertebral Strength Changes as Assessed by Finite Element Analysis

Fig. 5.1

Schematic representation why small loss in BMD could result in big loss in mechanical strength of the whole bone and why small gain in BMD could contribute to big gain in strength. (a) Original bone pillar. (b) Even a small crack could severely affect the bone strength, while the loss in BMD is relatively small. (c) If the treatment could add bone at the crack, strength may be restored while gain in BMD is small

BTMs reflect the pharmacological responses to osteoporosis therapies and are taking an increasingly important role in patient management; however, there are no consensus views to characterize high and normal bone turnover. For some analyses, the premenopausal reference range has been used to define a normal range, but there is a wide overlap between pre- and postmenopausal women, and a large overlap between those who will fracture compared with those that remain fracture free. The poor predictive value of BTMs in fracture risk suggests that absolute values for BTMs are not suited as treatment targets, at least with current technologies, while the change in BTMs would be useful as an index of compliance shortly after the onset of treatment [2].

The FRAX ® tool has been developed by the World Health Organization (WHO) to evaluate fracture risk of individual patients from studying population-based cohorts from Europe, North America, Asia, and Australia. The FRAX® algorithms give the 10-year probability of fracture, however, unable to detect the impact of treatment on fracture risk [2].

As such, treatment has no clear consensus goal for BMD, BTMs, or fracture risk up until now. So understandably, the US Food and Drug Administration (FDA) still requires evidence for fracture risk reduction over 3 years as compared to placebo for registration of treatments for postmenopausal osteoporosis – a prohibitively expensive, and perhaps unethical, place for patients, clinical investigators, and industry research and development to be put at this time [3].

Given these limitations, there is a substantial interest in developing improved means for clinical assessment of bone strength. In this sense, finite element analysis is one of the best candidates up until now. The FEA technique is successful primarily because it biomechanically integrates all of the 3-dimensional geometry and density information within the CT scan. Promising data suggest that a more trustworthy surrogate marker of bone strength, such as FEA, could possibly substitute for fracture endpoints [1, 4].

5.2 Finite Element Analysis for Osteoporosis

FEA is a powerful numerical technique widely used by engineers and scientists for understanding the mechanics of physical systems. Engineers employ FEA to simulate how a physical system will respond to the expected loading conditions with an advantage of being applicable to solids of irregular geometry that contain heterogeneous material properties. Practical applications of FEA include structural analysis of various buildings, crash analysis of automobiles, aerodynamic analysis of airplanes, fluid flow analysis in channels and pipes, and so on. FEA in this osteoporosis field was first applied to live patients in a clinical research study in the early 1990s and used since then in many orthopedic biomechanical studies. With advances in the imaging modality and the processing power of computers, FEA has become more accessible and as such is becoming an increasingly popular tool to address questions about structure–function relationships in the bone field. FEA has been used for various parts of the body including skeletal sites at high risk of osteoporotic fractures: the spine, hip, wrist, or more microscopically trabecular column, or individual trabeculae.

Typical analytical procedures of voxel-based FE analysis of CT scans of vertebra are as follows:

Step 1: Modeling

Firstly, subject-specific CT-based finite element model (Fig. 5.2) is generated by converting the QCT (quantitative computed tomography) scans. Each vertebra image is rotated into a standard coordinate system, thresholded, calibrated, and converted into an isopropic 1 × 1 × 1-mm voxel-type finite element mesh using 8-noded brick elements with material properties derived directly from the calibrated mineral values in each element. More specifically, gray-scale Hounsfield unit data in the standard DICOM (Digital Imaging and Communications in Medicine)-formatted CT image is converted into calibrated values of BMD. Such material property–density relations are typically derived from cadaver experiments, adjusted to account for side artifacts, and elastic anisotropy of the bone was accounted for by assuming fixed ratios of the various elastic constants with respect to the longitudinal modulus. Material failure of the bone is modeled by assigning an elastic–perfectly plastic von Mises failure criterion to the bone [5, 6].

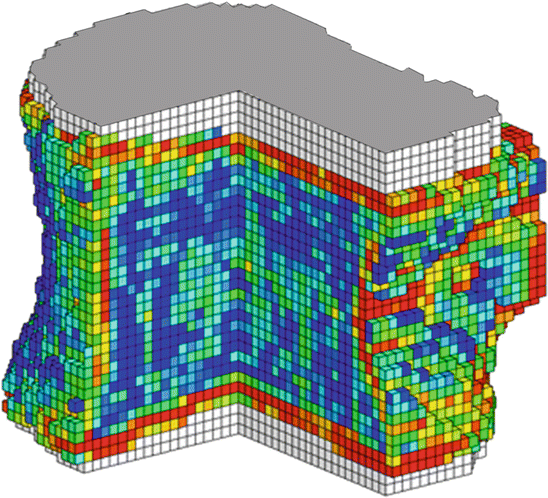
Fig. 5.2

Voxel-based FE model or a whole vertebral body from QCT scan, with individual finite elements color-coded according to their local material strength values

The finite elements themselves can be hexahedral-shaped replicas or scaled versions of the voxels, can be tetrahedral or curved, and can employ either linear or quadratic nodal-displacement formulation [1].

In order to take cortical shell into consideration, one approach would be the use of the thin element (Fig. 5.3) and another would be high-resolution image-based FEA. The former has inherent limitations since the cortical shell does not have a uniform thickness and has a porous structure. The latter may be able to account for microarchitecture; however, such high-resolution in vivo imaging in routine practice raises concerns about radiation dosage [1].

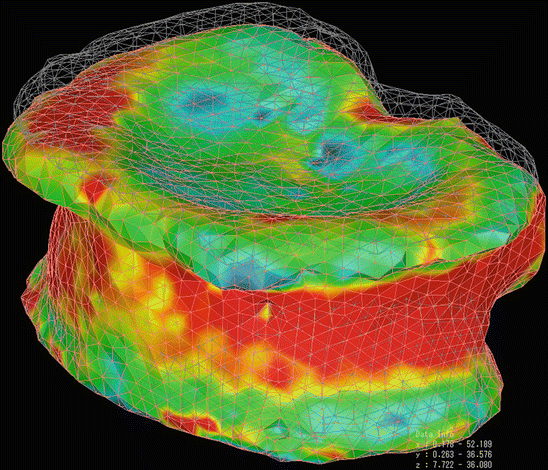
Fig. 5.3

FE model of a whole vertebral body from QCT scan, structured with tetrahedral elements. The cortical shell was modeled by using triangular plates with a thickness of 0.4 mm

Step 2: Boundary and Loading Conditions

Secondly, boundary and loading conditions are applied to the model. When the model simulates an in vitro compressive-strength test, a thin layer of polymethylmethacrylate (PMMA) is virtually placed at the ends of each model vertebra to simulate test conditions commonly used in compressive-strength testing of cadaver vertebrae. In addition, another loading condition could be used to assess the bending structural behavior of the vertebra [5, 6].

Step 3: Calculation and Interpretation of the Outcome

Finally, nonlinear FEA is performed on models to compute strength, defined as the total reaction force generated at an imposed displacement equivalent to an overall vertebral compressive strain of 2 % (applied displacement divided by height). These techniques have been shown to provide excellent predictions of vertebral compressive strength [7]. When nonlinear finite element analysis is used, spatial distribution of failed bone material and bone damage within the whole bone can also be assessed, which can provide insight into the type of fracture to be expected under the prescribed loading conditions.

To assess compressive strength changes associated with changes only in the trabecular compartment, trabecular strength values could be calculated by removing the outer 2 mm of the bone from the model (which includes the thin cortical shell and adjacent trabecular bone) and recomputing strength for the remaining trabecular compartment. While it is impossible to directly calculate the strength associated with the cortical bone, the strength for the peripheral compartment could be estimated by subtracting the trabecular compartment strength from the whole vertebral compressive strength [6].

Alternatively, Imai et al. defined vertebral fracture as being at least one element failed, which occurs when the minimum principal strain of the first element was less than −10,000 microstrain, during application of uniaxial compressive load with a uniform distribution and a uniform load increment. They analyzed the yield load, the fracture load, the sites where elements failed, and the distribution of minimum principal strain [8].

5.3 Validation Study

Before applying this new technique to human clinical study, cadaver validation is required.

Crawford et al. found that vertebral strength and stiffness from in vitro mechanical testing using 13 vertebral specimens were positively correlated with FEA-predicted strength and stiffness (r ² = 0.86 P < 0.0001, r ² = 0.82 P < 0.0001, respectively) [7].

Imai et al. verified their method using a quasi-static uniaxial compression test of 12 thoracolumbar vertebral specimens. The FEA-predicted yield loads, fracture loads, and minimum principal strains were significantly correlated with those measured in cadaver study (r = 0.949 P < 0.0001, r = 0.978 P < 0.0001, r = 0.838 P < 0.0001, respectively) [8].

As such, reported cadaver studies have consistently shown that FEA of CT scans provides excellent predictions of vertebral compressive strength. Because of its projective and scalar nature, the performance of BMD in predicting bone strength depended on loading mode and was significantly inferior to FEA. The positive results of these biomechanical studies in vitro provided solid ground for its use in cross-sectional or prospective clinical studies [4].

5.4 FE Strength vs. aBMD

When comparing FE-estimated strength and aBMD by DXA, Mawatari et al. reported that baseline values of FE strength were poorly correlated with baseline values of aBMD (R ² = 0.39, P = 0.0002) [6]. Moreover, the weak correlation has reported between individual changes in aBMD by DXA and individual change in FE strength.

Several studies indicate that the decrement in strength is relatively large compared with that in BMD [5, 6]. On the contrary, the increment in strength in response to treatment is relatively large, whereas the increment in BMD is modest. So evaluation of osteoporosis by BMD may underestimate the change in strength.

The available evidence indicates that treatment effects can be detected earlier and with greater statistical power (lower P values) by FEA because of improved statistical sensitivity [1].

5.5 FEA Using HR-pQCT

While QCT-based FEA represents a promising mechanistic alternative to densitometric techniques in accurately estimating the strength of the bone and predicting osteoporotic fracture risk, the voxel size often used for the current FE model was not small enough to explicitly capture such details as trabecular thickness, spacing, and connectivity or the true geometry of the cortical shell.

While a clinical CT is able to scan the human spine with minimum resolution of 150–350 μm, the voxel size is not high enough for taking individual trabecular structures or thin cortical shell into account. Several studies tried to use μCT and HR-pQCT images in combination with FE technique. High-resolution CT as the imaging technique requires a high X-ray dose of ~3 mSv but offers the possibility to generate high-resolution models as well as analyze the bone structure of a central fracture site, the spine. A lower effective dose would be possible if dedicated peripheral CT was used. This technique allows for a better image quality, but only at peripheral sites such as the forearm [9].

Dall’Ara has reported the HR-pQCT-based μFE and QCT-based nonlinear homogenized voxel-based FE for the same set of cadaveric spines [10]. The HR-pQCT (0.082 × 0.082 × 0.082 mm³ voxel size) images were segmented after the application of a Laplace–Hamming filter with a fixed 40 % threshold, and the voxels were then directly converted to hexahedral elements. This model is able to account for trabecular microstructure, but due to the high amount of time and resources needed to run the μFE, only linear analysis was feasible for large samples. Linear μFE models were solved with ParFE on a Cray XT3 using 256 CPUs in parallel. While both HR-pQCT-based μFE and QCT-based FE predicted material properties better than aBMD, the latter provided reasonable quantitative estimations of the experimental mechanical properties without fitting the model parameters [10].

When the image resolution is improved to 82 μm, no benefits were found for prediction of any vertebral mechanical property using densitometric variables, and a significant improvement was only seen only for prediction of stiffness using linear μFE.

In vivo image voxel size for the human spine of 82 μm with a reasonable radiation dose is not expected in the close future [10].

5.6 Treatment Efficacy Assessment

5.6.1 Alendronate vs. Teriparatide for Postmenopausal Osteoporosis [5]

Both antiresorptives including alendronate (ALN) and anabolic agent such as teriparatide (TPTD) are reported to increase aBMD and reduce fracture risk, while underlying mechanisms on bone remodeling are opposite. Keaveny et al. have demonstrated the effect of TPTD and ALN on 3rd lumbar vertebral bone strength by comparative study using the FE modeling of QCT scans. Also trabecular strength values were calculated by removing the outer 2 mm of bone from the model and recomputing strength for the remaining trabecular compartment.

In an 18-month active comparator study of 53 patients (N = 28 TPTD 20 μg/day; N = 25 ALN 10 mg/day), both treatments had positive effects on vertebral compressive strength. At 18 months, the median percentage increase for TPTD was 5.7-fold greater from baseline compared with ALN, 21.1 % versus 3.7 %. Both treatments also increased the strength–density ratio from baseline, but the median percentage increases were three to five times larger for the TPTD group (6.01 % versus 2.15 %, p = 0.002). Comparison of change in the FEA vertebral compressive strength versus the change in aBMD indicated that DXA did not capture well the changes in biomechanical properties that occurred with treatment and that, in general, the relation between BMD changes and FEA strength changes depended on treatment. They concluded that both TPTD and ALN increased vertebral strength, while larger increases in the strength–density ratio were also observed for TPTD, and these were primarily attributed to preferential increases in trabecular strength. This is the first study that compares two approved treatments for osteoporosis on FE-derived biomechanical measurements of the spine in a clinical setting.

5.6.2 Alendronate for Rheumatoid Arthritis [6]

Osteoporosis occurs more frequently in patients with rheumatoid arthritis (RA) than in otherwise healthy individuals. Treatment with antiresorptive agents such as ALN is the generally accepted recommendation for prevention and treatment of osteoporosis in RA patients who are receiving glucocorticoids; significant reductions in the risk of incident radiographic vertebral fractures have been found with ALN treatment. However, the biomechanical mechanisms by which ALN treatment alters vertebral strength in RA and the relative effect of such treatment on the cortical versus the trabecular compartment remain unclear. A prospective randomized clinical trial was undertaken to compare strength changes, measured using FEA, in rheumatoid arthritis (RA) patients who were treated with ALN versus those who were not. Nonlinear finite element analysis was performed on the CT scans of L₃ vertebra (n = 29) to compute an estimate of compressive strength and to assess strength changes associated with changes in the trabecular compartment and the outer 2 mm of bone (peripheral compartment).

As a result, vertebral strength was significantly decreased from baseline in the control group (median change −10.6 %; P = 0.008) but was maintained in the ALN group (median change +0.4 %; P = 0.55), with a significant difference between the two groups (P < 0.01). Strength decreased more rapidly within the trabecular bone, and ALN treatment was much more effective in the peripheral than the trabecular compartment. Mawatari et al. concluded that patients with RA can lose a substantial amount of vertebral strength over a relatively short period of time, and this loss can be prevented by ALN, primarily via its positive effect on the outer 2 mm of vertebral bone.

5.6.3 Alendronate for Postmenopausal Osteoporosis [11]

Imai et al. analyzed vertebral strength in 104 postmenopausal Japanese women in vivo using QCT-based nonlinear FE model with 2-mm tetrahedral elements and 2-mm triangular plates on the outer surface of the cortical shell and explored the discriminatory power for vertebral fracture cross-sectionally. They also prospectively assessed the effects of ALN by this technique in 33 patients with postmenopausal osteoporosis who were treated with ALN for 1 year.

On the age- and body weight-adjusted logistic regression, estimated 2nd lumbar vertebral strength had stronger discriminatory power for vertebral fracture (OR per SD change: 6.71) than aBMD and vBMD. Calculated vertebral fracture threshold was 1.95 kN with 75.9 % sensitivity and 78.7 % specificity. ALN effects were detected on vertebral strength at 3 months (+10.2 % from baseline). At 1 year, the density of the inner cancellous bone increased by 8.3 %, while the density of the juxtacortical areas increased by 13.6 %.

They concluded that QCT-based nonlinear FEM had higher discriminatory power for vertebral fracture than BMD and detected ALN effects as early as 3 months. ALN altered density distribution and decreased the area with a high fracture risk, resulting in increased vertebral strength.

5.6.4 Ibandronate for Postmenopausal Osteoporosis [12]

This 1-year randomized, double-blind, placebo-controlled study investigated the effects of once-monthly oral ibandronate (IBN) on both the hip and spine in postmenopausal osteoporosis by 3D techniques of QCT and FEA and the 2D techniques of DXA and hip structure analysis (HSA). Women aged from 55 to 80 years old with BMD T-score −2.0 or less to −5.0 or greater were randomized 1:1 to receive oral IBN 150 mg (n = 47) or placebo (n = 46) once monthly for 12 months.

IBN increased vertebral, peripheral, and trabecular strength and anterior and posterior bending stiffness vs. placebo [7.1 % (P < 0.001), 7.8 % (P < 0.001), 5.6 % (P = 0.023), and 6.3 % (P < 0.001), respectively], while lumbar spine aBMD increased more with IBN than placebo [4.3 % (P < 0.001)]. FE-derived hip strength to density ratio and femoral strength, as well as total hip QCT BMD and DXA aBMD, also increased with IBN vs. placebo. HSA-estimated femoral narrow sectional area and moment of inertia and outer diameter increased with IBN vs. placebo. Lewiecki et al. concluded that once-monthly oral IBN for 12 months improved hip and spine BMD measured by QCT and DXA and strength estimated by FEA of QCT scans.

Only gold members can continue reading. Log In or Register to continue