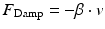Fig. 3.1
The mandible (jaw). On the left is a sectioned image of the mandible when viewed from above and on the right is the lateral perspective [4]
The hyoid bone is another U-shaped bone situated in the neck between the chin and thyroid cartilage. It provides an attachment point for muscles that have their insertions at the floor of the mouth or beneath the mandible. The hyoid bone itself is not fixed, but suspended by muscles in the anterior, posterior and inferior directions. However, its service as an anchoring point for tongue movement, swallowing and other mandibular movements suggests that relative to the mandible, it is quite stationary. If the maxilla and hyoid are assumed to be fixed in space, and the mandible is able to move freely between them except for where it is fixed to the maxilla at the temporomandibular joints (TMJs), then the interaction between the mandible and actuating muscles is similar to a parallel robot platform [2].
3.1.2 Mandibular Muscles
The masticatory system contains a large number of muscles, to the extent where it almost seems that there are more muscles than required to perform functional mandibular movements. From a mechanical perspective this may seem to be an inefficient arrangement, but the spatial limitations native to the masticatory system have to be considered. The confined space in the craniofacial region means that if the muscular system were to be in a mechanically optimal arrangement it would most likely interfere with the adjacent airways and digestive tract [3]. To compensate, the masticatory muscles are generally more complex than the skeletal muscle within other limbs. They have a multipennate structure, are complexly layered or are divided into active regions. The complexity addresses the non-ideal physical arrangement of the muscles and allows substantial differential contractile forces to be produced by the mandible.
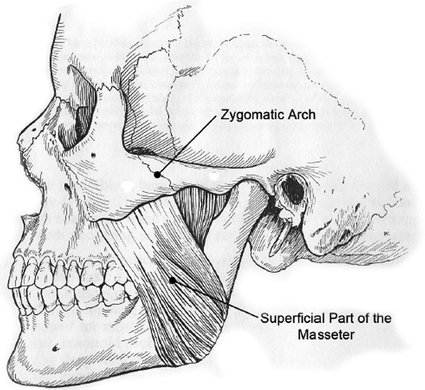
The masseter is a bulky, rectangular muscle that is located on the lateral side of the mandible. It lies just beneath the surface of the skin and its cross section is wedge-shaped and bulky. The masseter can be divided into two parts in relation to their functional purposes: the superficial head and the deep head. Its origin is at the zygomatic arch of the skull and its insertion is at the lateral surface of the ramus (the ascending part of the mandible), as shown in Fig. 3.2. The muscle has a multipennate structure, where muscle fibres converge towards a central tendon on multiple sides, similar to a feather. This structure vastly increases muscle power and gives a broader range of directional pull.
In general, the masseter is used for the heavy crushing and grinding of food and primarily moves in the vertical direction. In addition to this, the masseters (on both sides of the jaw) are capable of exerting a range of forces in the anterior direction of the jaw and the deep head can produce retrusive movements (in the posterior direction) [4]. The superficial head of the masseter is the most likely contributor to surface EMG signal recordings and it is heavily involved in the mandible’s ability to produce bite forces up to and in excess of 590 N (mean for males with standard deviation of 145.8 N [5].
The largest mandibular muscle, though not considered one of the power movers of the mandible, is the temporalis. Its origin is fan-shaped which results in it being very large and covers a wide area, as shown in Fig. 3.3. Converse to its origin, the attachment of the temporalis to the mandible is concentrated on a smaller area on the ramus. When viewed laterally, the temporalis can be separated into three regions: the anterior, middle and posterior, and it can be divided further into two layers, the superficial layer and the principal mass. The bulk of the muscle lies in the anterior region and the tendinous fibres are generally longer than those of the masseter. The problem with the fan-shaped arrangement of the temporalis is that only a few fibres will be aligned with the direction of movement at any one time, reducing maximum efficiency. However, this means that besides producing a vertical pull on the mandible, there is the possibility of other directions of movement in the sagittal and frontal planes. The temporalis acts primarily as an elevator and retractor, but due to the divergent arrangement of fibres, it also has the ability to contribute to the fine adjustment of the mandible antero-posteriorly, medio-laterally and vertically [4].
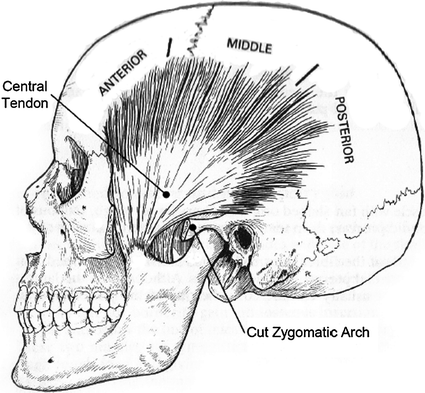

Fig. 3.3
The temporalis muscle [4]. Note that the anterior, middle and posterior sections are all part of the temporalis muscle
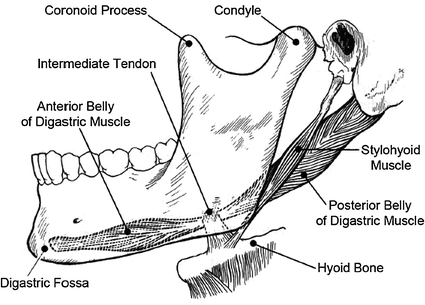
The digastric muscle has a unique structure and is formed from two belly-like masses of muscle tissue which are joined and separated by an intermediate tendon, as shown in Fig. 3.4. The anterior belly is smaller and is attached to the digastric fossa of the mandible while the posterior belly is attached to the mastoid notch of the temporal bone. The intermediate tendon is indirectly attached to the hyoid bone by a fascial tunnel, formed from a loop of cervical fascia. This structural arrangement is much like a pulley and allows the intermediate tendon to slide to and fro. The mechanism allows the digastric muscle to exert inferior and posterior traction and it is speculated that the two digastric muscles acting together, help to guide the mandible in a centred position as it approaches the intercuspal position during normal function. In these circumstances they act as antagonists to the action of the elevators and have the ability to guide the mandible laterally and medially, similar to the reins guiding a horse. The digastrics are the main depressors of the mandible and act as the antagonists to perform the controlled closure of the mandible. They are also active during positioning movements of the mandible in the transverse plane, including medial, lateral, protrusive and retrusive movements, and therefore appear to be the prime movers and antagonistic controllers in the horizontal plane [4].
3.1.3 The Temporomandibular Joint (TMJ)
In the craniofacial region there are 209 joints, 119 of which are synarthrodial (fibrous), 82 are special dental and eight are diarthrodial. The TMJ consists of a diarthrodial joint, which is a discontinuous arrangement and accommodates functional movements between bones [4].
Diarthrodial joints are subjected to shearing, abrasive and compressive forces and in order to withstand these forces they need to have strong and rigid articulating surfaces that maintain their shape. The ranges of movement of these joints are determined structurally and depend on how ligaments are attached, bone morphology, muscle activity and other structural restraints. The TMJ consists of a number of bony parts and soft tissue components. The bony parts include the condylar process of the mandible and the glenoid structures on the skull base. The condylar process can be seen in Fig. 3.4 and its function is to provide a supportive platform for the articular surface of the mandible. This is so that it can efficiently act as a pivot for three dimensional movement and as a fulcrum for third class leverage. It also provides suitable attachment points for the muscles which protract from the mandible. The glenoid structures are a group of several structural forms in the skull base that approximately match the condylar process and also serve as guides for condylar movement [4].
The soft tissue components of the TMJ include the articular covering of the joint surfaces, the articular disc and muscle tissue, the joint capsule, ligaments, synovial membranes, blood vessels and nerves. The articular disc is a continuous structure that occupies the space between the bony and articular surfaces of the joint. It is shown in Fig. 3.5 and it has three distinct parts of varying thickness. The posterior band is the thickest and is separated from the anterior band by the intermediate zone of the disc which is quite thin. The anterior and posterior bands act together with lateral and medial thickenings of the disc to form a self-centring mechanical wedging arrangement that keeps the disc on the condyle [6].
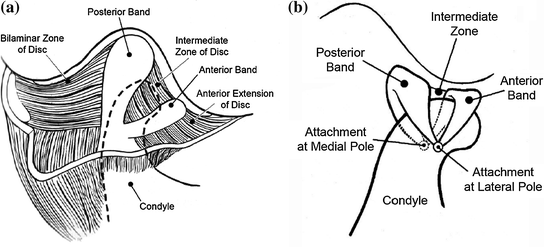

Fig. 3.5
The articular disc of TMJ. a Is the view in the sagittal plane. b Shows the details of the attachment points of the disc to the condyle. Adapted from [4]
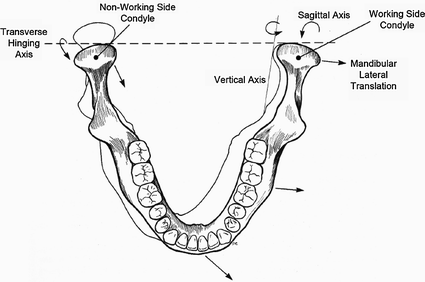
The capsule of the TMJ is a loose, tapering, thin-walled cuff of white collagenous tissue that encloses the bony parts and the articular disc, and delineates two joint cavities [4]. In the inferior joint compartment created by the capsule of the TMJ, the condyles can rotate about a horizontal axis. This is part of the simple hinge movement of the mandible in the vertical plane and it occurs through the bilateral movement happening simultaneously at both TMJs. In the superior joint compartment, the condyle-disc assembly is a firmly bound and closely adapted mechanism that is able to slide in the joint compartment due to the slack nature of the joint capsule. This allows the condyle-disc assembly to perform a range of movements that include sliding along the articular eminence, pivoting and rotating around a vertical axis and sliding medio-laterally. Additionally, because the joint capsule is quite loose, different movements can occur simultaneously in the superior compartments of the right and left joints. This is shown in Fig. 3.6 and exemplified through lateral movement where the condyle-disc assembly on the side the mandible is moving towards, pivots. On the opposite side, from which the mandible is moving away, the condyle-disc assembly progresses antero-inferiorly and medially (which is a translatory movement). The pivoting and translation occurs in the superior joint compartments and at the same time, in the inferior joint compartments, a simple hinge movement of varying extent occurs [4].
3.2 Masticatory System Physiological Model Development
Exoskeleton development for the masticatory system is in its infancy with only a very recent transition from robotic chewing devices to exoskeletal pursuits [7]. The original purposes of these chewing robots were to study mandibular dynamics and control methods for dental training, jaw simulation, food texture and breakdown analysis, and speech therapy [8]. Modelling of the masticatory system has been done in a similar fashion with the intention of understanding the underlying biomechanical processes and forces [3, 9]. These models are able to include the key mandibular muscles because accessibility is not an issue and can therefore explore the full range of available movement.
3.2.1 Revised Musculotendon Model
The musculotendon models are re-applied and it is assumed that muscular structure does not significantly vary around the body—the main difference is the size while structural and compositional proportions remain similar. This model provides the embodiment of a Hill-type muscle model, derived from experimental data, and consists of passive elastic (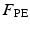 ) and viscous force components (
) and viscous force components (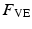 ), and an active contractile element (
), and an active contractile element (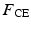 ), according to the relationships as follows:
), according to the relationships as follows:
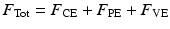
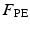 ) and viscous force components (
) and viscous force components (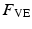 ), and an active contractile element (
), and an active contractile element (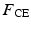 ), according to the relationships as follows:
), according to the relationships as follows: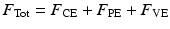
(3.1)
The force from the contractile element of the muscle can be found using:
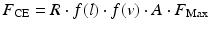
where 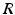 is a subject-specific parameter that accounts for differences in muscle size and strength,
is a subject-specific parameter that accounts for differences in muscle size and strength, 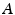 is the normalised activation level of the muscle from the EMG signal,
is the normalised activation level of the muscle from the EMG signal, 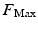 is the maximum force that can be produced by the muscle and
is the maximum force that can be produced by the muscle and 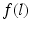 and
and 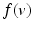 are the muscle force-length and force-velocity relationships, respectively.
are the muscle force-length and force-velocity relationships, respectively.
(3.2)
 is a subject-specific parameter that accounts for differences in muscle size and strength,
is a subject-specific parameter that accounts for differences in muscle size and strength,  is the normalised activation level of the muscle from the EMG signal,
is the normalised activation level of the muscle from the EMG signal,  is the maximum force that can be produced by the muscle and
is the maximum force that can be produced by the muscle and 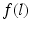 and
and 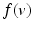 are the muscle force-length and force-velocity relationships, respectively.
are the muscle force-length and force-velocity relationships, respectively.Compared to the biceps and triceps however, the mandibular muscles are limited by the spatial limitations of the craniofacial region, making them smaller, and arranged differently to other joint systems. This provides different normalized and optimised length characteristics and the force-length relationship was adjusted from Eq. (3.3) to:
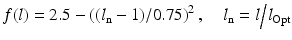
where 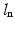 is the normalized muscle length given by the current muscle length,
is the normalized muscle length given by the current muscle length, 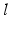 , and the optimum muscle length,
, and the optimum muscle length, 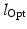 . The adjustment allowed more flexibility in the range of movement of the mandibular muscles to prevent model instabilities.
. The adjustment allowed more flexibility in the range of movement of the mandibular muscles to prevent model instabilities.
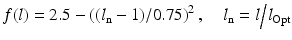
(3.3)
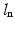 is the normalized muscle length given by the current muscle length,
is the normalized muscle length given by the current muscle length, 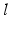 , and the optimum muscle length,
, and the optimum muscle length, 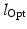 . The adjustment allowed more flexibility in the range of movement of the mandibular muscles to prevent model instabilities.
. The adjustment allowed more flexibility in the range of movement of the mandibular muscles to prevent model instabilities.The effect is shown in Fig. 3.7, where it is apparent that the previous equation presented for the elbow joint would lead to a representation of the musculotendon behaviour that is incongruous with actual dynamic processes. Muscle lengths extending or decreasing beyond the x-axis intercepts would cause a negated output and cause the model to behave unexpectedly or become unstable. The direction of the forces produced by each musculotendon unit is along the axis that connects the insertion and origin points of the musculotendon unit. Therefore, when considering three dimensional arrangements of the musculotendon units and the effect this has on the movement of a particular DOF, the total force needs to be broken down into its appropriate components.
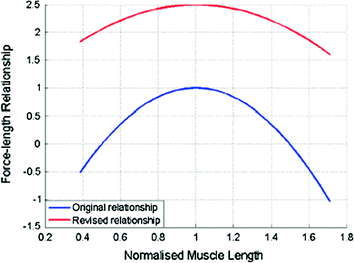

Fig. 3.7
Updated musculotendon force-length relationship. The shallower curve allows for a greater range of muscle length change
3.2.2 Jaw Musculoskeletal Model Derivation
The preliminary structure of the model was first built in the biomechanical simulation software environment, ArtiSynth [10], because a pre-existing detailed model of the jaw and laryngeal structure had previously been developed, as shown in Fig. 3.8a. This first model had a single degree of freedom and two lumped actuating muscle groups classified as jaw elevators and jaw depressors acting on an ‘L’ shaped representation of the mandible as shown in Fig. 3.8b. The muscle groups had geometries and attachment points to the mandible that were determined from the masseter and digastric muscles, with origins at fixed points in space (equivalent to maxilla and hyoid bone anchorage positions). This provided the attachment locations of the muscle groups, and approximate muscle lengths and bone geometry were obtained from the literature [11].
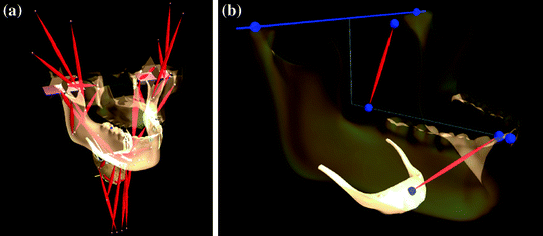

Fig. 3.8
Screenshots of ArtiSynth models. a Original model of the jaw and laryngeal structure. b Simplification of the masticatory system to a hinge joint
The motion of the mandible at this stage is purely rotational and a polar coordinate system was used to define the muscle attachment locations and incisor point (jaw geometry) relative to the centre of rotation. Figure 3.9 shows this arrangement in the sagittal plane with the elevator and depressor muscle groups acting on a mandible representation with a hinge joint at the centre of rotation. The polar coordinate system provides a means of easily determining the movement of dynamic properties of interest such as the incisor point (indication of opening angle), muscle group lengths and insertion points.
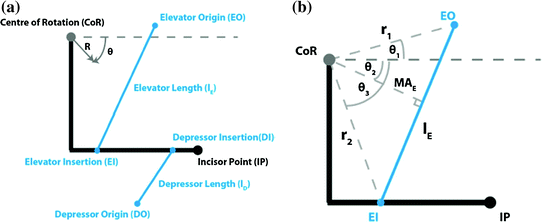

Fig. 3.9
Sagittal view of the musculoskeletal model. The model consists of the mandible and an antagonistic muscle group: elevator and depressor. a Labelling and coordinate system. b Elevator muscle group geometry
From the figure, it is apparent that because movements are only rotational, point locations only undergo rotational changes, and this is exemplified through the elevator muscle group. The insertion point on the mandible 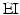 is the only point that moves as the origin
is the only point that moves as the origin 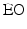 remains fixed to the maxilla. The length of the elevator muscle group (
remains fixed to the maxilla. The length of the elevator muscle group (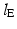 ) can therefore be determined geometrically and is given by:
) can therefore be determined geometrically and is given by:
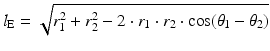
where (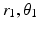 ) and (
) and (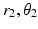 ) are the polar co-ordinates to the elevator origin and insertion, respectively, as indicated in the figure. The length of the depressor muscle group can be found with a similar expression but the origin and insertion coordinates would represent those of the depressor points instead.
) are the polar co-ordinates to the elevator origin and insertion, respectively, as indicated in the figure. The length of the depressor muscle group can be found with a similar expression but the origin and insertion coordinates would represent those of the depressor points instead.
 is the only point that moves as the origin
is the only point that moves as the origin 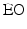 remains fixed to the maxilla. The length of the elevator muscle group (
remains fixed to the maxilla. The length of the elevator muscle group (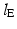 ) can therefore be determined geometrically and is given by:
) can therefore be determined geometrically and is given by: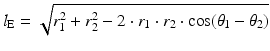
(3.4)
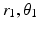 ) and (
) and (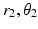 ) are the polar co-ordinates to the elevator origin and insertion, respectively, as indicated in the figure. The length of the depressor muscle group can be found with a similar expression but the origin and insertion coordinates would represent those of the depressor points instead.
) are the polar co-ordinates to the elevator origin and insertion, respectively, as indicated in the figure. The length of the depressor muscle group can be found with a similar expression but the origin and insertion coordinates would represent those of the depressor points instead.To determine total joint torque, the moment arms of the muscle groups still need to be calculated and these depend on the position of the mandible itself. The following is the derivation of the moment arm for the elevator muscle group (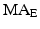 ), with labels illustrated in Fig. 3.10b. In general, if a line (
), with labels illustrated in Fig. 3.10b. In general, if a line (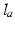 ) passes through the pole (origin) of a polar coordinate system and is perpendicular to a line (
) passes through the pole (origin) of a polar coordinate system and is perpendicular to a line (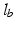 ) with an intersection at point (
) with an intersection at point (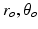 ) and the point (
) and the point (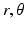 ) lies on
) lies on 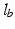 , the equation for
, the equation for 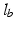 is given by:
is given by:

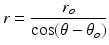
 ), with labels illustrated in Fig. 3.10b. In general, if a line (
), with labels illustrated in Fig. 3.10b. In general, if a line (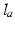 ) passes through the pole (origin) of a polar coordinate system and is perpendicular to a line (
) passes through the pole (origin) of a polar coordinate system and is perpendicular to a line (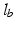 ) with an intersection at point (
) with an intersection at point (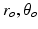 ) and the point (
) and the point (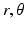 ) lies on
) lies on 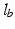 , the equation for
, the equation for 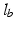 is given by:
is given by:
Fig. 3.10
Examples of jaw positions in the sagittal plane. Note the variation in muscle lengths and the fixed locations of the origin muscle attachment points. a Jaw open. b Jaw closed (occluded)
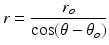
(3.5)
Note that it is assumed l b does not pass through the pole itself and this relationship can be used to provide two definitions for the muscle group length and its perpendicular line through the pole, which utilise the known origin and insertion coordinates of the elevator muscle group:
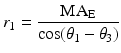
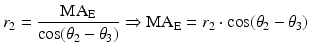
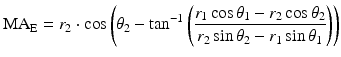
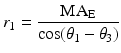
(3.6)
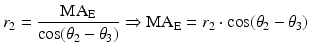
(3.7)
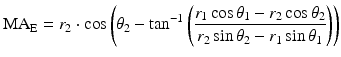
(3.8)
Movement of the mandible will affect angle 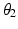 since the position of EO is fixed. The pure rotational movement also means that
since the position of EO is fixed. The pure rotational movement also means that 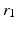 and
and 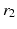 , once defined for an individual, remain constant throughout all movements. The moment arm for the depressor muscle group with origin and insertion points at DO and DI, respectively, and the moment arm MAD can be derived in a similar fashion, but with the coordinates (
, once defined for an individual, remain constant throughout all movements. The moment arm for the depressor muscle group with origin and insertion points at DO and DI, respectively, and the moment arm MAD can be derived in a similar fashion, but with the coordinates (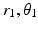 ), (
), (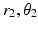 ) and (
) and (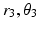 ) representing DI, DO and MAD respectively:
) representing DI, DO and MAD respectively:
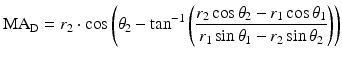
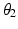 since the position of EO is fixed. The pure rotational movement also means that
since the position of EO is fixed. The pure rotational movement also means that 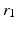 and
and 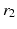 , once defined for an individual, remain constant throughout all movements. The moment arm for the depressor muscle group with origin and insertion points at DO and DI, respectively, and the moment arm MAD can be derived in a similar fashion, but with the coordinates (
, once defined for an individual, remain constant throughout all movements. The moment arm for the depressor muscle group with origin and insertion points at DO and DI, respectively, and the moment arm MAD can be derived in a similar fashion, but with the coordinates (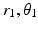 ), (
), (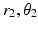 ) and (
) and (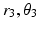 ) representing DI, DO and MAD respectively:
) representing DI, DO and MAD respectively: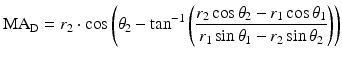
(3.9)
Up to this point, the weight of the mandible has not been considered, and it would be inappropriate to ignore its effect since movements are occurring in the sagittal plane. The difficulty, however, lies in determining the mass of the mandible and its attached muscles, and even approximating its centre of gravity is dependent on many factors. The passive activity of antagonistic muscles during movement contributes to moments of inertia and the suspension of the jaw by multiple muscles means that its mass is distributed. The inability to measure mass and inertial properties directly, or even estimate them with reasonable accuracy, means that values from the literature will have to be sought and combined with subject-specific parameters to account for variability and the inevitable inaccuracy. The weight can be assumed as acting at a single point and is attributed to the mass of the mandible and attached tissues that are part of the moving system. If the weight acts at the point (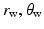 ), the resulting moment arm is:
), the resulting moment arm is:
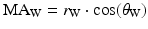
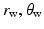 ), the resulting moment arm is:
), the resulting moment arm is: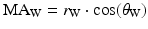
(3.10)
Deriving the weight of the mandible from its approximated mass allows the determination of the resulting moment:
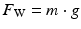
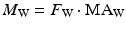
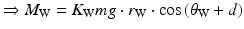
where m is the approximate mass of the mandible, K W is a subject-specific parameter to account for modelling inaccuracies, and d is the opening angle of the mandible which affects the position of the centre of gravity. The elevator, depressor and weight forces are enough to produce single DOF rotation motion in the sagittal plane. The ArtiSynth model in different stages of opening is shown in Fig. 3.10, and the lengthening and shortening of the muscle groups is apparent. The movement of the mandible will naturally be rotational but the trajectory of the incisor point does not necessarily have to follow a circular pattern. Additional passive degree of freedom, such as a vertical translational component that is dependent on the opening angle of the mandible, could allow more realistic trajectories with a shallower arc to be produced by the model [12].
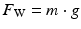
(3.11)
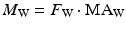
(3.12)
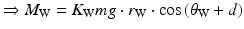
(3.13)
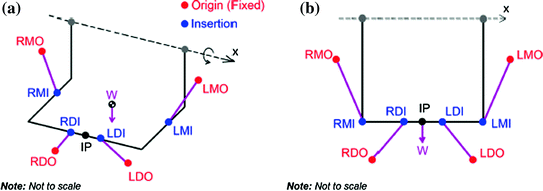
The model was developed to have two degree of freedom: open-close movement (about a hinge joint with fixed centre of rotation, denoted by CoR and about the x axis in Fig. 3.11) and lateral movements, where the mandible translates in the horizontal direction (along the x axis in Fig. 3.11). The position of the mandible was measured by the movement of the incisor point (IP in the figure), in cylindrical co-ordinates (R, 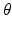 , x), which was the most convenient system to simultaneously output the predicted movements.
, x), which was the most convenient system to simultaneously output the predicted movements.
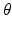 , x), which was the most convenient system to simultaneously output the predicted movements.
, x), which was the most convenient system to simultaneously output the predicted movements.
Fig. 3.11
2-DOF musculoskeletal model of the jaw. The 2-DOFs are given by rotation about and translation along the x axis. (R, 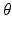 , x) is the cylindrical coordinate system, W is the weight of the mandible, and the labels consist of combinations of: R right, L left, M masseter, D digastric, I muscle insertion and O muscle origin. EMG signals are therefore required from the bilateral masseters and digastrics. The view from the sagittal plane remains unchanged. a Top-left view. b Frontal view
, x) is the cylindrical coordinate system, W is the weight of the mandible, and the labels consist of combinations of: R right, L left, M masseter, D digastric, I muscle insertion and O muscle origin. EMG signals are therefore required from the bilateral masseters and digastrics. The view from the sagittal plane remains unchanged. a Top-left view. b Frontal view
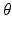 , x) is the cylindrical coordinate system, W is the weight of the mandible, and the labels consist of combinations of: R right, L left, M masseter, D digastric, I muscle insertion and O muscle origin. EMG signals are therefore required from the bilateral masseters and digastrics. The view from the sagittal plane remains unchanged. a Top-left view. b Frontal view
, x) is the cylindrical coordinate system, W is the weight of the mandible, and the labels consist of combinations of: R right, L left, M masseter, D digastric, I muscle insertion and O muscle origin. EMG signals are therefore required from the bilateral masseters and digastrics. The view from the sagittal plane remains unchanged. a Top-left view. b Frontal viewFor force and torque calculations, the forces are broken down into their respective components relevant to the degree of freedom of motion being calculated. Both DOFs of movement, however depend on the lengths of the muscles and the definition of attachment points in cylindrical coordinates allows the model to be expanded easily to accommodate this (in the sagittal plane, the model looks unchanged and the x axis can be considered to only add depth). The total length of a muscle group is given by:
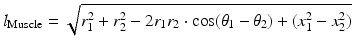
where 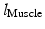 is the length of any muscle group given the coordinates of its origin (
is the length of any muscle group given the coordinates of its origin (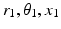 ) and insertion (
) and insertion (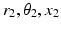 ). The final implementation of the musculoskeletal model was in the MATLAB/Simulink environment where the mass and overall passive properties of the mandible were introduced to the model and were similar to the values used in the elbow model.
). The final implementation of the musculoskeletal model was in the MATLAB/Simulink environment where the mass and overall passive properties of the mandible were introduced to the model and were similar to the values used in the elbow model.
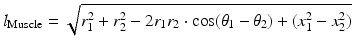
(3.14)
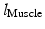 is the length of any muscle group given the coordinates of its origin (
is the length of any muscle group given the coordinates of its origin (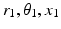 ) and insertion (
) and insertion (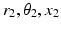 ). The final implementation of the musculoskeletal model was in the MATLAB/Simulink environment where the mass and overall passive properties of the mandible were introduced to the model and were similar to the values used in the elbow model.
). The final implementation of the musculoskeletal model was in the MATLAB/Simulink environment where the mass and overall passive properties of the mandible were introduced to the model and were similar to the values used in the elbow model.3.2.3 Kinematic Model
The concept of using kinematics in a rotational and translational capacity is applied here for the opening–closing and lateral movements, respectively. The total joint moment can be determined by combining the appropriate components of the forces calculated from the musculotendon models with the moment arms from the musculoskeletal model, and the horizontal components can be used to determine the forces contributing to lateral movement. For the opening and closing movement, the moments produced by each musculotendon unit is:
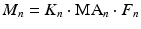
where n = LM, RM, LD or RD, and the moment is given by the product of the force component in the sagittal plane determined from the musculotendon model, F n , the moment arm determined from the musculoskeletal geometry, MA n , and a subject-specific parameter to account for inaccuracies in the geometric model, K n . The total joint moment can then be determined using:
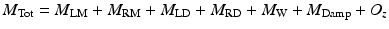
where the total moment about the centre of rotation, M Tot, is given by the sum of moments caused by the left masseter (LM), right masseter (RM), left digastric (LD), right digastric (RD), mandible weight (W), joint damping (Damp) and an offset value that determines resting position in the vertical direction, O z . The kinematics of the joint can now be found with:
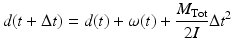
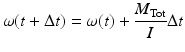
where the new angular displacement (in the 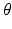 direction) of the mandible,
direction) of the mandible, 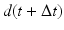 , on the previous displacement d(t), previous angular velocity
, on the previous displacement d(t), previous angular velocity 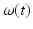 , moment of inertia II, and sampling time
, moment of inertia II, and sampling time 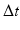 . Note that up to this point calculations have been implemented in polar coordinates so, to obtain the vertical displacement, z(t), a geometric conversion is required that uses the (R,
. Note that up to this point calculations have been implemented in polar coordinates so, to obtain the vertical displacement, z(t), a geometric conversion is required that uses the (R, 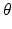 ) coordinates of the incisor point:
) coordinates of the incisor point: 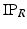 and
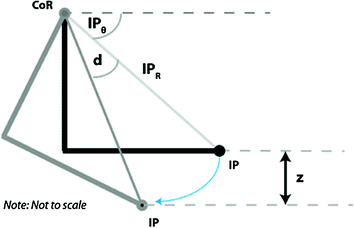
and 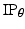 respectively. The vertical displacement of the mandible is necessary for comparisons with data from the literature and actual measurements of jaw movement because the concept of a rotational angle, while based on anatomical structure, is largely arbitrary when considering the distance between the approximated centre of rotation and incisor point. The vertical displacement is shown in Fig. 3.12, and given by:
respectively. The vertical displacement of the mandible is necessary for comparisons with data from the literature and actual measurements of jaw movement because the concept of a rotational angle, while based on anatomical structure, is largely arbitrary when considering the distance between the approximated centre of rotation and incisor point. The vertical displacement is shown in Fig. 3.12, and given by:
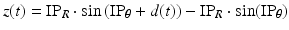
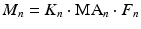
(3.15)
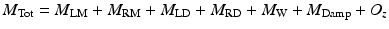
(3.16)
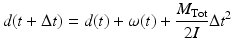
(3.17)
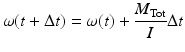
(3.18)
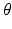 direction) of the mandible,
direction) of the mandible, 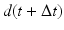 , on the previous displacement d(t), previous angular velocity
, on the previous displacement d(t), previous angular velocity 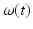 , moment of inertia II, and sampling time
, moment of inertia II, and sampling time 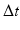 . Note that up to this point calculations have been implemented in polar coordinates so, to obtain the vertical displacement, z(t), a geometric conversion is required that uses the (R,
. Note that up to this point calculations have been implemented in polar coordinates so, to obtain the vertical displacement, z(t), a geometric conversion is required that uses the (R, 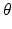 ) coordinates of the incisor point:
) coordinates of the incisor point: 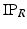 and
and 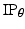 respectively. The vertical displacement of the mandible is necessary for comparisons with data from the literature and actual measurements of jaw movement because the concept of a rotational angle, while based on anatomical structure, is largely arbitrary when considering the distance between the approximated centre of rotation and incisor point. The vertical displacement is shown in Fig. 3.12, and given by:
respectively. The vertical displacement of the mandible is necessary for comparisons with data from the literature and actual measurements of jaw movement because the concept of a rotational angle, while based on anatomical structure, is largely arbitrary when considering the distance between the approximated centre of rotation and incisor point. The vertical displacement is shown in Fig. 3.12, and given by:
Fig. 3.12
Determination of vertical displacement, z
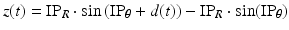
(3.19)
The translational component of movement is found with similar relationships, but along the x axis. The horizontal force components of the muscles is found by determining the horizontal component of the muscle forces in the x direction, using the acute angle between the force vector and x axis, 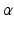 . The vertical distance is given by:
. The vertical distance is given by:
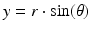
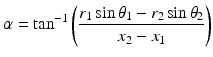
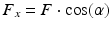
where 1 and 2 are subscripts for insertion and origin cylindrical coordinates, and F x is the lateral component of total musculotendon force, F. Once all the horizontal force components are known, the total force in the lateral direction can be determined and linear kinematics applied to find the horizontal displacement and velocity:
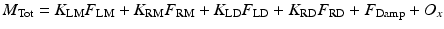
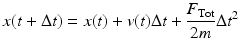
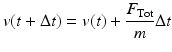
where the total force, F Tot, is determined by the sum of the force components in the x direction, with the addition of O x to account for lateral force offset and subject specific K i parameters (i = LD, RD, LM, RM) to account for the difference in muscle sizes and strengths. The horizontal displacement 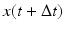 and velocity
and velocity 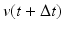 is calculated using the previous displacement, x(t), velocity, v(t), and mandible mass, m. The horizontal motion also requires its own damping component that accounts for the passive viscous and elastic damping properties of the masticatory system that affect horizontal movement:
is calculated using the previous displacement, x(t), velocity, v(t), and mandible mass, m. The horizontal motion also requires its own damping component that accounts for the passive viscous and elastic damping properties of the masticatory system that affect horizontal movement:
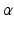 . The vertical distance is given by:
. The vertical distance is given by: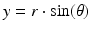
(3.20)
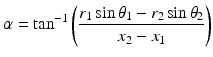
(3.21)
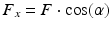
(3.22)
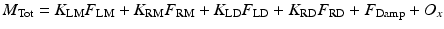
(3.23)
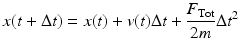
(3.24)
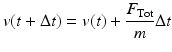
(3.25)
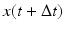 and velocity
and velocity 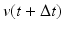 is calculated using the previous displacement, x(t), velocity, v(t), and mandible mass, m. The horizontal motion also requires its own damping component that accounts for the passive viscous and elastic damping properties of the masticatory system that affect horizontal movement:
is calculated using the previous displacement, x(t), velocity, v(t), and mandible mass, m. The horizontal motion also requires its own damping component that accounts for the passive viscous and elastic damping properties of the masticatory system that affect horizontal movement: