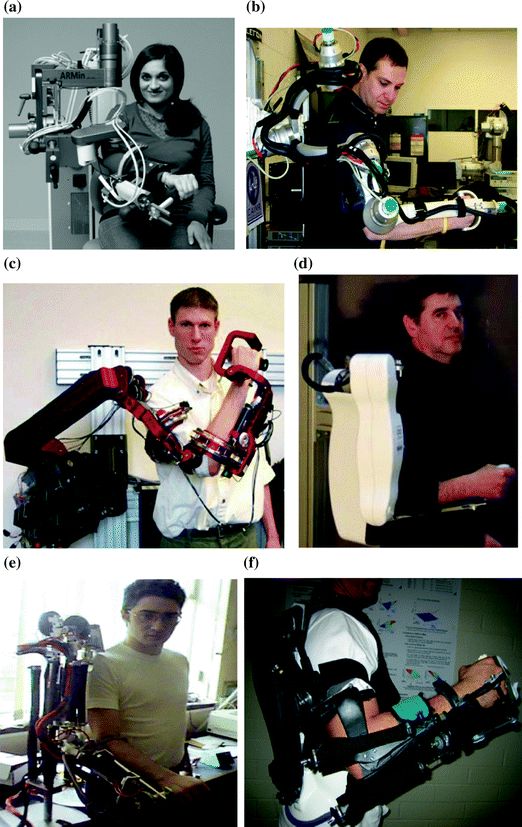
Exoskeletons have a structure that resembles the human upper limb, having robot joint axes that match the upper limb joint axes as shown in Fig. 2.1b. Exoskeletons are designed to operate alongside the human upper limb, and therefore can be attached to the upper limb at multiple locations. Although this can make it more difficult for the robot to adapt to different arm lengths, multiple interfaces allow the exoskeleton to fully determine the upper limb posture and apply controlled torques to each upper limb joint independently. It is possible for exoskeletons to target specific muscles for training by generating a calculated combination of torques at certain joints. In addition, a larger range of motion is possible compared to end-effector robots which enable a wider variety of movements to be used in rehabilitation exercises.
The majority of past upper limb exoskeletons focus on movements for the 3-DOF spherical rotation of the shoulder joint and 1-DOF of the elbow. A lower number of exoskeletons have included movements for the 3-DOF wrist joint and even fewer have included movements for the 2-DOF translations of the shoulder joint. One exoskeleton studied during this literature review has also included 1-DOF for grasping movement of the hand. From this, it can be seen that the upper limb DOF that has larger influence on the hand’s position have been the focus of upper limb exoskeletons. Rehabilitation of these movements is of the highest priority since they are the most important in controlling the position of the hand.
The ARMin III (Fig. 2.2a) [11], MGA [12] (Fig. 2.2b) and IntelliArm [13] exoskeletons have implemented an actuated DOF for shoulder elevation & depression. The MEDARM has included actuation for both shoulder elevation and depression, and retraction and protraction, allowing 5-DOF of actuated movement at the shoulder complex [14]. Other groups have opted to use passive DOF for these translation movements [13, 15, 16]. Passive DOF allows the joint to move freely but eliminates the ability to generate actuation forces at the joint.
There are a number of commercially available rehabilitation devices for the upper limb. One of the more sophisticated rehabilitation devices available are the Armeo products (Hocoma AG, Switzerland) [17]. These include the 7-DOF ArmeoPower active exoskeleton, ArmeoSpring passive exoskeleton and ArmeoBoom sling suspension system. The ArmeoPower is based on the ARMin III exoskeleton [11]. Examples of other commercial devices include the mPower arm brace (Myomo, Inc., Cambridge, MA) [18], a 1-DOF portable arm brace which uses electromyography (EMG) signals measured from the biceps and triceps muscles to generate assistive torques for elbow flexion and extension, and the Hand Mentor (Kinetic Muscles, Inc., Tempe AZ) [19], a 1-DOF wearable device for the rehabilitation of the wrist and fingers which provides force, position and EMG feedback and is actuated by an air muscle. The Robot Suit HAL-5 (Cyberdyne Inc., Japan) is a full-body exoskeleton for the disabled which uses measured EMG signals from the user to generate assistive torques. Examples of commercial end-effector rehabilitation robots include the InMotion robots (Interactive Motion Technologies, Inc., Boston, MA) [20], Biodex System 4 dynamometer (Biodex Medical Systems, Inc., New York) [21], HUMAC NORM (SCMi, Stoughton, MA) [22] and CON-TRES MJ (CMV AG, Switzerland) [23].
2.1.2 Ankle Rehabilitation Robots
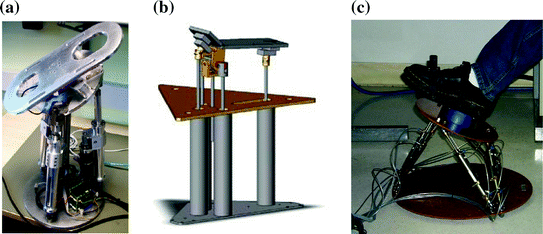
Robotic devices had been developed for the rehabilitation of the human ankle. Although the main rehabilitation problem considered in this research is that of sprained ankle rehabilitation, devices used for gait rehabilitation for neurological disorders are also considered in this discussion for completeness. Ankle rehabilitation devices can be classified into two categories in terms of the mobility of the device during operation. These are wearable robots and robotic platforms with stationary bases. Wearable ankle robots typically take the form of a robotic orthosis or exoskeleton (Fig. 2.3) and are used to correct the user’s gait pattern. Robotic platforms (Fig. 2.4) on the other hand, manipulate the user’s foot using their end-effectors and are generally developed to facilitate the treatment of ankle sprains.
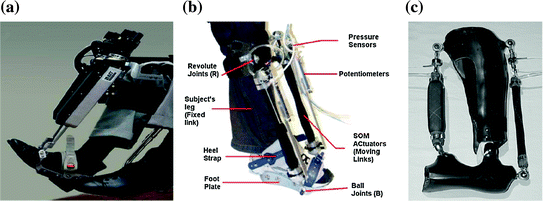

2.1.2.1 Wearable Ankle Rehabilitation Robots
To enable their use in gait rehabilitation, robotic devices developed for preventing foot drop must be wearable. It must also be controlled to limit the downward rotation of the foot during certain phase of gait. It is therefore not surprising that many robots used in this capacity take the form of actuated orthoses or exoskeletons. While some of these devices provide actuated motion in only 1-DOF to influence foot plantarflexion and dorsiflexion [35–38], others also include the possibility of controlled or passive inversion and eversion movements [9, 39, 40]. The internal-external rotation of the foot, however, is rarely controlled as it is assumed to be a negligible component of gait.
The actuators used in wearable ankle robots developed in the literature are typically of lower inertia to allow higher mobility due to the wearable nature of the device. The actuators are also chosen to be inherently backdrivable to ensure the safety of the user. An example of such actuators is the series elastic actuators used in [35, 38]. This family of actuators is constructed by placing an electric motor in series with a compliant elastic element. The compliant element therefore isolates the motor inertia from the actuator end point inertia and the force applied by the actuator can be regulated by controlling the deformation of the compliant element. These actuators are normally used with stiffness control and are in general utilised to influence the mechanical behaviour of the ankle joint rather than to provide large assistive moments.
Pneumatic muscle is another type of actuator commonly used in wearable ankle robots due to its high power-to-weight ratio and inherent compliance. It is typically used in systems with higher moment capacity, thus allowing these devices to provide a greater level of assistance during the user’s gait. The disadvantage, however, is the requirement of a source of compressed air and the non-linear dynamics of the actuators. Both position control [30] and proportional myoelectric control [31, 36, 37] strategies had been applied on systems using pneumatic muscles. Position control is generally used to drive the length of the muscles to values which correspond to the desired foot configuration/orientation while proportional myoelectric control activates the pneumatic muscles according to the myoelectric signals measured from the user/patient’s leg muscles.
Some notable features can also be identified in the wearable ankle robots considered in this review. The first is the incorporation of some element of intelligence into these devices. For example, adaptability was introduced in [35] to improve the performance of the AFO by adjusting the AFO stiffness to reduce the occurrences of drop foot gait, while the previous gait velocity is used in [38] to generate references for subsequent gait cycles. Additionally, knowledge of the general gait pattern had also been incorporated in higher level control schemes which coordinate the switching of AFO behaviour according to the current phase of gait.
Another important feature worth noting can be found in the mechanical designs of [9, 30, 40], where the AFOs were designed to be under-actuated when not attached to the user/patient. The advantage of this is that it will not be necessary to align the AFO’s kinematic constraints to those of the human ankle, thus allowing the device to cater for a wider range of users and reducing set-up time. Furthermore, with an appropriate design, the device will be able to provide control or support in the important degree of freedom while at the same time acting passively in the remaining directions. This therefore helps to maintain natural movement of the ankle-foot structure and ensures that no unnecessary constraints are imposed on the user’s ankle-foot complex.
2.1.2.2 Platform-Based Ankle Rehabilitation Robots
A range of platform-based devices had also been developed by researchers for the purpose of sprained ankle rehabilitation [41, 42]. They are therefore designed to carry out various ankle rehabilitation exercises such as motion therapy and muscle strength training. Motion therapy can be divided into passive, active-assist and active exercises, each requiring a different level of participation from the patient, ranging from no active effort in the passive exercises to full user-driven motion in active exercises. Strength training requires the robot to apply a resistive load to impede the user’s movement to improve muscle strength.
One of the key differences between these platform-based devices and the wearable devices discussed previously is that the platform-based devices have a fixed base and thus cannot be used during gait training. Given the rather limited range of motion at the ankle-foot complex, parallel mechanisms are typically used for multiple DOF systems to reduce the size of the robot. With the exception of the Stewart platform-based device proposed in [43] which is capable of 6-DOF motion, most researchers have opted for designs which offer 2- or 3-DOF in rotational motion, where robot movements in the yaw direction (internal-external rotation) are typically constrained on 2-DOF devices. Most of the lower DOF devices also include a central strut in the robot’s kinematic structure to provide the kinematic constraint required to restrict the movement of the end effector so that it is purely rotational [41, 44].
Different actuators had been used in platform-based ankle rehabilitation robots. The Stewart platform-based device in [43] and the reconfigurable ankle rehabilitation platform in [33] have utilised pneumatic cylinders to provide actuation, while electric motors were used in devices developed in [41, 45, 46]. A custom-designed electric actuator was proposed in [32, 48] to improve actuator backdrivability, whereby a cable-driven pulley system is used to convert the rotational motion of a DC motor to linear motion of the actuator rod.
A variety of control schemes had been implemented on these platform-based ankle rehabilitation robots. One approach involves the use of either pure force or pure position control for the execution of different exercises [43]. For instance, position control of the platform is typically used for passive range of motion ankle exercises where the user’s foot is guided by the robot along the prescribed rehabilitation trajectory, or for isometric exercises where the orientation of the robot is kept constant while the user exerts a particular moment on the robot. Force control on the hand is used to maintain a desired level of interaction torque between the user and the robot during resistive or assistive exercises. Impedance/admittance control strategies had also been implemented, usually through a position-based approach whereby the robot’s reference trajectory is modified based on the desired robot impedance and the measured interaction forces/moments [32, 33, 47, 48]. Such control schemes are also generally used with a computed torque/inverse dynamics based position controller to allow accurate tracking of the desired reference trajectories. While the basic interaction control schemes had been implemented on existing platform-based ankle rehabilitation robots, little emphasis had been placed on the realisation of adaptive control in such devices to allow adjustment of the robot behaviour due to variation in the user’s joint characteristics and capability.
2.1.3 Rehabilitation Robots for Masticatory System
There is no specific medical condition called “jaw motion disorder”. For the scope of this book, jaw motion disorder will be used to describe a deviation from ideal or normal function of the masticatory system, due to a single factor or combination of pathologies that affect mandibular movement. The causes of this dysfunctional movement can be from temporomandibular joint disorder (TMJD), which is an affliction of the TMJ, or paralysis or weakening of mandibular muscle.
TMJD is also known as myofascial pain dysfunction or Costen’s syndrome and it is mostly caused by habitual behaviours that place excessive wear on the TMJ, trauma, disease or wear from aging [49, 50]. It is estimated that at any one time in the USA, 10 million people suffer from TMJD, making it a major health problem [51]. The symptoms and effects of TMJD are numerous and affect other areas in the craniofacial region as well as the mandible itself. Symptoms such as headaches, ear pain, dizziness, fullness of the ear (where the ear feels clogged) and tinnitus (ringing in the ear) can all be caused by TMJD. More intuitively, TMJD also causes muscle pain, pain within the TMJ and grinding, crunching or popping sounds [49]. Pain in the facial muscles and jaw joints can also be extended to the neck or shoulders. The most significant effect, however, is on the actual motion of the mandible. TMJD reduces the range of motion, causing the mandible to not fully open or to deviate to one side during opening. These unnatural movements feel awkward and affect the nature of occlusion [50].
Besides TMJD, the other significant contributing factor to jaw motion disorder is a loss in mandibular muscle function and this can be due to a weakened or paralysed muscle or group of muscles. The causes of detrimental mandibular muscle function are no different from those of other muscles within the body, and include muscular dystrophy (MD) [52], muscular atrophy [53] and stroke.
Most of the pathologies described in this section which contribute to jaw motion disorder can be treated with varying degrees of physical therapy. The therapy has to be tailored to a particular patient and should suit their specific needs. Passive motion therapy followed by active therapy can help strengthen and increase the movement range of muscle. However, existing aids are not sufficient at emulating all the motions that may be required for mastication and a more sophisticated device is required that accommodates the multiple DOFs of the mandible to restore mandibular function in rehabilitative processes.
2.2 Human Musculoskeletal Models
2.2.1 Movements of Upper Limb
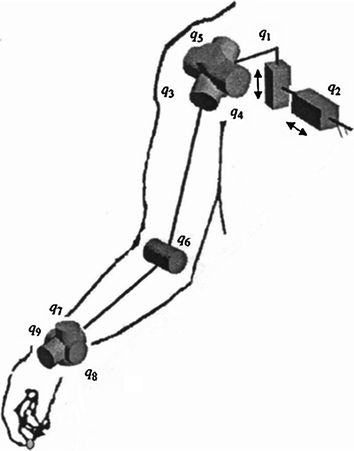
Operating alongside the human upper limb, exoskeletons need to be capable of producing movements similar to those of the upper limb. The upper limb effectively has a total of 9-DOF from the shoulder to the wrist with the finger joints excluded as shown by 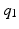 to
to 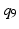 in Fig. 2.5 [54, 55]. This 9-DOF gives the upper limb exceptionally high manoeuverability and allows the hand to reach a very large workspace. The proximal joints of the upper limb are often considered a higher priority for rehabilitation as these joints have the largest influence on the hand’s position and provide support for the rest of the limb.
in Fig. 2.5 [54, 55]. This 9-DOF gives the upper limb exceptionally high manoeuverability and allows the hand to reach a very large workspace. The proximal joints of the upper limb are often considered a higher priority for rehabilitation as these joints have the largest influence on the hand’s position and provide support for the rest of the limb.
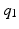 to
to  in Fig. 2.5 [54, 55]. This 9-DOF gives the upper limb exceptionally high manoeuverability and allows the hand to reach a very large workspace. The proximal joints of the upper limb are often considered a higher priority for rehabilitation as these joints have the largest influence on the hand’s position and provide support for the rest of the limb.
in Fig. 2.5 [54, 55]. This 9-DOF gives the upper limb exceptionally high manoeuverability and allows the hand to reach a very large workspace. The proximal joints of the upper limb are often considered a higher priority for rehabilitation as these joints have the largest influence on the hand’s position and provide support for the rest of the limb.The shoulder joint has 5-DOF, 3-rotational DOF which allow spherical rotation of the upper arm and 2-translational DOF which move the upper arm along the vertical axis and the anterior–posterior axis. The movements of each DOF are commonly described by a pair of terms, one for movement in the positive direction and one for the negative direction:
Shoulder flexion
Rotation of the upper arm about the shoulder ICOR (instantaneous centre of rotation) out of the plane of the torso so that it points forwards.
Shoulder extension
Rotation of the upper arm about the shoulder ICOR out of the plane of the torso so that it points backwards.
Shoulder abduction
Rotation of the upper arm about the shoulder ICOR in the plane of the torso so that it is lifted upwards.
Shoulder adduction
Rotation of the upper arm about the shoulder ICOR in the plane of the torso so that it is dropped downwards.
Shoulder medial rotation
Axial rotation of the upper arm towards the torso.
Shoulder lateral rotation
Axial rotation of the upper arm away from the torso.
Shoulder elevation
Translation of the shoulder ICOR upwards.
Shoulder depression
Translation of the shoulder ICOR downwards.
Shoulder protraction
Translation of the shoulder ICOR forwards.
Shoulder retraction
Translation of the shoulder ICOR backwards.
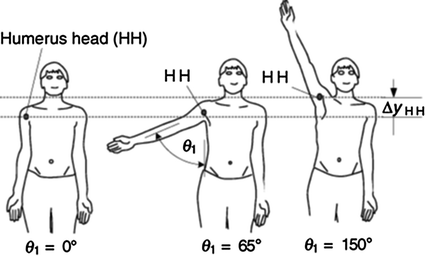
An interesting phenomenon of the shoulder is that abduction of the upper arm above the horizontal plane will occur simultaneously with elevation as shown in Fig. 2.6 [56]. Without this elevation, abduction above the horizontal plane cannot be achieved.
The elbow joint has 1-rotational DOF which moves the forearm with the following movements:
Elbow flexion
Rotation of the forearm about the elbow joint so that the forearm is moved closer to the upper arm.
Elbow extension
Rotation of the forearm about the elbow joint so that the forearm is moved further from the upper arm.
The wrist joint has 3-rotational DOF allowing the hand to rotate spherically about the wrist joint. The movements are described as:
Wrist flexion
Rotation of the hand about the wrist joint towards the palm.
Wrist extension
Rotation of the hand about the wrist joint away from the palm.
Wrist radial deviation
Rotation of the hand about the wrist joint towards the thumb.
Wrist ulnar deviation
Rotation of the hand about the wrist joint away from the thumb.
Forearm pronation
Rotation of the hand about the axis of the forearm so that the palm faces backwards when the hand is pointing downwards.
Forearm supination
Rotation of the hand about the axis of the forearm so that the palm faces forwards when the hand is pointing downwards.
2.2.2 Model of Ankle Joint
Kinematics of the ankle-foot complex had been extensively studied in the literature. The simplest representation of ankle-foot motion is that of a hinge joint perpendicular to the sagittal plane. This description considers the entire foot as a rigid body that can rotate about the shank in the plantarflexion and dorsiflexion directions. This is a gross oversimplification of the ankle-foot motion as movements in other DOF are ignored. Additionally, early studies had found from examination of the talus bone surface geometry that the axis of rotation of the talus will vary with its orientation [58, 59]. The actual kinematics of the foot is therefore very complex as it is governed by the articulating surfaces between the different foot bones, as well as constraints imposed by ligaments, tendons and soft tissues. This was highlighted in various studies which investigated the movement patterns of foot bones in terms of 6-DOF motion in either in vitro or in vivo scenarios [60–63]. The general findings of these works were that the axes of rotations of the ankle and subtalar joints do vary rather considerably between different foot orientations and different individuals/specimens. Additionally, translational motions of the joint centres were also recorded, although it was found that these movements are typically within the range of one to two centimetres.
Information of ankle kinematics is essential in applications such as gait analysis, diagnosis of normal ankle-foot function and design of implants for total ankle replacement. However, the complex motion observed at the ankle makes it difficult to describe the complete ankle kinematics concisely with a mathematical model. Models of varying levels of complexity had been established for different applications. As discussed above, the simplest model used is that of a single hinge joint model (Fig. 2.7a). Furthermore, ankle-foot motion had been described as purely rotational using an effective spherical joint (Fig. 2.7b) [64], while the biaxial model which considers the foot motion to be equivalent to rotations about two hinge/revolute joints in series was also widely adopted in literature (Fig. 2.7c) [64–69]. Additionally, recent studies had modelled the ankle-foot kinematics using four-bar linkages and spatial parallel mechanisms [63, 70].
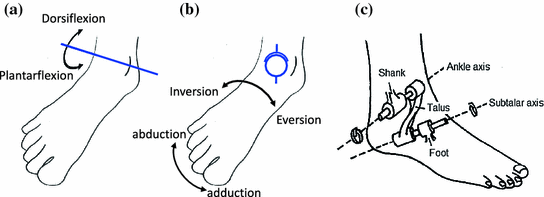

Fig. 2.7
Kinematic models used to describe ankle motion. a Hinge joint model. b Spherical joint model. c Biaxial joint model. Adapted from [65]
Since large inter-subject variability is observed in ankle kinematics, a user-specific description of ankle kinematics should be used to adapt the robot behaviour to suit the current user. Most of the studies in literature that considers subject-specific ankle kinematics in full 6-DOF have utilised either motion tracking systems or medical imaging techniques [71, 72]. As these methods typically require offline processing, they are not suited for use in real-time systems. A simpler kinematic model with reduced degree of freedom which is amenable to online parameter identification is therefore more appropriate for this research. Additionally, since this representation of the ankle kinematics will also be incorporated in the dynamic model of the ankle-foot structure, the use of a straightforward model will reduce the computational complexity of the system, thus making its simulation more tractable. For the above reasons, the biaxial ankle model appears to be sensible choice and its parameter estimation will be further discussed.
Parameter identification for a biaxial kinematic model was investigated by van den Bogert in an in vivo manner using visual markers placed on the subject’s foot [68]. The biaxial model considered has 12 parameters and these are determined through minimisation of the discrepancies between marker positions obtained from the assumed model and from measurements using the Levenberg–Marquardt algorithm. The resulting ankle and subtalar joint orientations using this method were found to be similar to corresponding values obtained from in vitro anatomical studies of the ankle. Good fit of the model in terms of the marker positions was also reported, with relatively small rigid body errors. Lewis et al. had also investigated the parameter identification of the biaxial ankle model on both biaxial mechanical linkage and cadaveric foot specimens [71]. The optimisation algorithm used is largely similar to that described by van den Bogert except that the ankle and subtalar joint displacements were estimated through optimisation using the Gauss–Newton algorithm. It was reported that the parameter identification of the biaxial mechanical linkages shows results that are largely consistent with the actual kinematic parameters of the structure. Considerable discrepancies, however, were observed between the ankle and subtalar joint orientations computed from the optimisation algorithm and the average helical axes obtained from successive measurements of the foot bone orientations. This had therefore led them to conclude that the biaxial ankle model with fixed revolute joints can only give a limited representation of the actual ankle-foot kinematics, and that an alternative model, perhaps one with configuration-dependent joint axes orientations, be explored. It should be noted that both the previous works discussed above on the identification of biaxial ankle kinematic model parameters were completed using offline optimisation techniques.
Studies in the biomechanical characteristics of the ankle go beyond the understanding the kinematic behaviour of the ankle. It seeks also to identify how the human ankle will react under certain loading conditions, as well as the loading distribution among different anatomical structures of the ankle-foot complex such as foot bones, ligaments, tendons and other soft tissues.
One of the core components of a computational ankle model is a description of the ankle-foot kinematics as it determines how the foot bones will move relative to one another, thus ultimately influencing the length of ligaments and muscle-tendon units, as well as deformation of other soft tissues. While the use of three-dimensional contact constraints [73–75] can lead to more realistic results, it can be computationally intensive and therefore limit the speed of simulations. In this aspect, the biaxial ankle kinematic model described previously appears to be able to provide a good balance between simplicity and the ability to provide a reasonably description of the ankle-foot motion.
Another important modelling decision is found in the treatment of bones and soft tissues. Some models treat the bones as rigid bodies and ignore effects caused by deformation of soft tissues [67, 73], while others apply finite element analysis on the bones and soft tissue in order to obtain the stress distribution across the articulating bone surfaces [74, 75]. Clearly, use of finite element analysis will improve the accuracy of the model at the expense of increased computational complexity.
Effects of ligaments on the ankle-foot biomechanics had also been considered in some models. Typically, they are treated as tension-only elastic elements whose lengths are dependent on the configurations of foot bones [73–75]. Some models, however, include the influence of ligaments on passive joint stiffness as a lumped effect, and describe it through application of non-linear resistive moment-displacement functions at the ankle and subtalar joints [76, 77]. Properties of muscles and tendons are also commonly included in computational models which require consideration of active muscular contractions [67, 76, 77], and these models typically employ a Hill-based muscle model and are often used for gait analysis. Models which involve explicit modelling of the ligaments and muscle-tendon units generally require the acquisition of bone geometry and ligament/tendon attachment locations by means of medical imaging, and this can add to the complexity of the model. However, as forces and strains along the ligaments/tendons can be extracted from such models, the added complexity can be justified for applications requiring greater insights into the loading on these anatomical elements.
2.2.3 Model of Masticatory System
The purpose of the human masticatory system is to perform the initial breakdown of food via chewing and prepare it for swallowing. It includes the bones and soft structures, such as muscles, ligaments and tendons of the face and mouth, that are involved in mastication. There are multiple complex mechanisms involved in this process, including the secretion of saliva, manipulation of the chewed food into a bolus with the tongue and the muscular control of the mandible that produces chewing motions, which is the focus of this and following parts. The main problem is that if the temporomandibular joint (TMJ) or mandibular muscles are weakened, the patient is unable to properly chew and process food. Current solutions include modifying the texture or consistency of the food for easier processing, or bypassing the masticatory system by tubular feeding through the oesophagus or abdomen. However, there are also efforts that are attempting to reduce the effects of physical symptoms through therapy and physical rehabilitation of the mandibular muscles. Similar to gait or upper limb rehabilitation, these exercises consist of repetitive exercises that are conducted with the assistance of a therapist, and can therefore also benefit from the advantages robotics and exoskeletons provided in those applications.
This section introduces the components of the masticatory system directly involved in the formation of chewing motions, including the skeletal structure, primary mandibular muscles and the temporomandibular joint. These components form a unique complex structure that is not replicated elsewhere in the human body and allows the mandible to be manipulated in three-dimensional space. A review of the available literature regarding masticatory robotics and the development of jaw exoskeletons for rehabilitation is also presented, which lead to the motivations behind this particular case study.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree