Fig. 18.1
Anatomy of the lower extremities
The three-dimensional motion of the hindfoot joints (Fig. 18.2) is clinically described as consisting of three anatomical planes of motion. Flexion occurs in the sagittal (X-Z) plane where dorsiflexion moves the superior (i.e. dorsal) surface of the foot towards the axis of the leg and plantarflexion moves the inferior (i.e. plantar) surface of the foot towards the axis of the tibia. Inversion and eversion occurs in the coronal (Y–Z) plane where inversion moves the plantar surface towards the median plane and eversion moves the plantar surface away from the median plane. Rotation of the foot occurs in the transverse (X–Y) plane where internal rotation moves the toes away from the median plane. During motion of the hindfoot, the joints of the ankle/foot complex work together rather than acting in isolation. While the hindfoot joints are often described as hinge joints, the true axis for this motion is not contained within any anatomical plane and changes orientation over the complete range of motion. In particular, flexion of the hindfoot joints is coupled to both rotation and inversion/eversion of the foot.
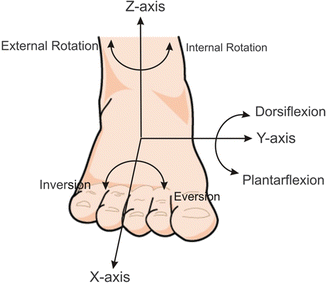

Fig. 18.2
Anatomical motions and coordinate axes of hindfoot joints
Foot and ankle anthropometry was collected in a study by Crandall et al. [1] from detailed measurements of cadavers tested at the University of Virginia (UVA) and Renault, as well as from a volunteer study conducted by Parham et al. [2] for the United States Army, and a compilation of studies by Diffrient et al. [3]. Measurements from the University of Virginia study were based on 39 male cadavers with an average mass of 77.5 ± 18.3 kg and an average stature of 175 ± 7.6 cm, and from Renault, based on 11 male cadavers, with an average stature of 175 ± 12 cm. The study by Parham et al. (n = 293) consisted of male soldiers with an average stature of 175.6 ± 7.1 cm and average mass of 75.7 ± 11.4 kg. The Diffrient et al. study was composed of volunteers with an average stature of 174.8 cm. A summary of detailed foot and ankle dimensions is shown in Table 18.1 (Fig. 18.3).
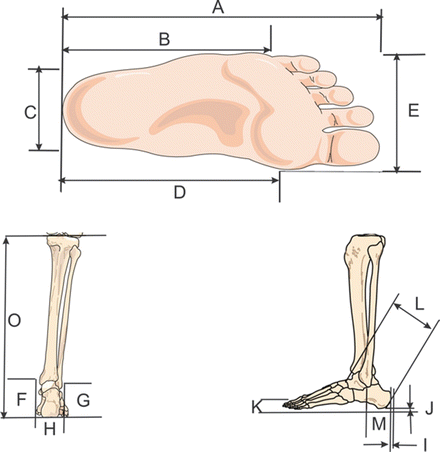
Table 18.1
Dimensions of the human foot and ankle
Label | Measurement | Study | Dimension (cm) |
|---|---|---|---|
A | Foot length | UVA [1] | 24.4 ± 1.5 |
B | Ball length (heel to head of 5th metatarsal) | Diffrient [3] | 16.3 |
C | Heel width | Parham [2] | 7.0 ± 0.44 |
D | Ball length (heel to head of first metatarsal) | Diffrient [3] | 19.6 |
E | Foot breadth at metatarsal-phalangeal joints | Parham [2] | 10.5 ± 0.56 |
F | Medial malleolus height form head to floor | UVA [1] | 8.3 ± 1.1 |
Medial malleolus height from tip to floor | UVA [1] | 8.3 ± 1.3 | |
G | Lateral malleolus height form head to floor | Parham [2] | 7.2 ± 0.29 |
Lateral malleolus height from tip to floor | UVA [1] | 6.9 ± 1.2 | |
H | Ankle width at level of medial malleolus | Diffrient [3] | 7.6 |
I | Soft tissue thickness from posterior heel to calcaneous | UVA [1] | 0.8 ± 0.4 |
J | Soft tissue thickness from distal heel to calcaneous | UVA [1] | 1.6 ± 0.4 |
K | Plantar arch height from floor | Parham [2] | 3.03 ± 0.60 |
L | Ankle length from heel to front of ankle (tibia) | Parham [2] | 10.8 ± 0.72 |
M | Heel to head of lateral malleolus | Diffrient [3] | 6.6 |
O | Tibia height from distal heel to tibial medial margin | UVA [1] | 47.0 ± 4.07 |

Fig. 18.3
Physical dimensions of the human foot and ankle
18.2 Automotive-Related Injuries
Lower limb injuries sustained during moderate-to-severe automobile collisions have occurred throughout history of the automobile as a result of toe-pan intrusion alone. Before the advent and wide-spread availability of air-bag equipped vehicles, the occupant was usually killed from head and thoracic trauma, so lower limb fractures were never well documented. As the number of air-bag equipped vehicles increased in the fleet, the number of collision survivors with serious lower limb injuries has seemingly increased. In fact, as the result of air-bags, injuries to the lower extremities have become the most frequent “non-minor” injury to happen in a frontal collision. Trauma to the foot and ankle make up approximately 30 % of these non-minor lower extremity injuries, and approximately 10 % of all non-minor injuries. Because of the frequency and severity of these lower limb injuries, significant research has been conducted over the last 20 years to understand the etiology and prevention of these injuries.
Similarly, there are approximately 15,000 hip injuries in the United States each year due to frontal crashes [4]. The study of Kuppa and Fessahaie [5] emphasizes that knee-thigh-hip injuries are the most common form of lower extremity injuries and are also the most life threatening due to the relatively high risk of severing an artery from the broken bones of the femur or pelvis.
Overall, the lower extremities represent the anatomic region most frequently injured in automobile collisions, and 20–30 % of these injuries occur at the knee as a result of contact with the knee bolsters of an automobile. Although less lethal than injuries to the head and neck, knee injuries result in significant recovery time and health care costs. Knee bolsters of varying stiffness are now common among automakers to reduce the load transmitted to the knee during a collision. Though protective of the knee, incorrect design of the knee bolster can shift the injury to the femur or hip.
As outlined in the beginning of this chapter, the biomechanics of the foot, ankle, and lower tibia/fibula involves a complex system of bones, ligaments, and load paths that depend not only on boundary conditions, but load rate and energy delivered to the foot as well.
18.2.1 Tibia/Fibula Response and Failure
The following section provides a review of both the publicly available literature and previous testing on the bending and axial load response and tolerance of the tibia-fibula complex. This section is meant to highlight the existing injury criteria and data available for finite element validation. This review of the leg/tibia/fibula is only concerned with whole bone/segment response to bending and axial load. Testing on the response and failure of the tibial plateau/condyles, the tibial plafond, and lateral and medial malleloli are discussed in the knee and ankle joint validation sections. For human finite element model validation of whole bone tibia/fibula and leg segment models, both the fracture tolerance and the structural bending response are discussed in the following sections.
18.2.1.1 Tibia/Fibula/Leg Fracture Tolerance in Bending
Numerous studies have been conducted to determine the structural fracture tolerance of the human leg in bending (Table 18.2). The studies report a significant variation in fracture tolerance that is likely due to both the wide variety of test conditions applied in the tests as well as variation in the human tissue specimens used. Injury risk functions that account for the applicable covariates are ideal for FE model validation of fracture/failure tolerance since they permit the application of conservative estimates, with statistical bases, to model simulations.
Table 18.2
Previous studies on the failure tolerance in bending of the tibia/fibula/leg
Study | Sample size | Fracture tolerance | Notes |
|---|---|---|---|
Weber 1859 in Nyquist 1986 [6] | 9 (4 M, 5 F) | 165/125 Nm (M/F) | Quasi-static, tibia only |
Messerer 1880 in Nyquist 1986 [6] | 12 (6 M, 6 F) | 207/124 Nm (M/F) | Quasi-static, tibia only |
Mather 1967 [7] | 16 | 3,244 (+/−783) N | Quasi-static, tibia only |
Mather 1968 [8] | 318 | 78.6 J/63.1 J (M/F) | Dynamic, energy required to fracture half of specimens tested |
Motoshima 1960 in Yamada 1970 [9] | 35 | 182 Nm | Quasi-static, females 5/6 as strong as males, bending tolerance same in all directions |
Nyquist et al. 1985 [10] | 10/9 (A-P/L-M bend) | 300/317 Nm (AP/LM) | Dynamic (2.1–4.7 m/s), Force data are filtered to cutoff of 100 Hz, L-M direction, with flesh and fibula |
Rabl et al. 1996 [11] | 16/5/5/6 (Ant/Lat/Med/Pos) | 5,787 N/6,430 N/6,117 N/4,556 N | Dynamic (0.3 m/s), moment/span not reported, constrained bone end boundary condition |
Schreiber et al. 1997 [12] | 10/12 (Q/D) | 241/408 Nm (Q/D) | Quasi-static and dynamic (5.6 m/s), P-A direction |
Kerrigan et al. 2003a [13] | 8 M (4 pairs) | 310 Nm | 1 Quasi-static, 7 dynamic (1.45 m/s), L-M direction, 1 with flesh and fibula and 7 only bare tibiae |
Kerrigan et al. 2003b [14] | 4/6 (Q/D) | 168/378 Nm (Q/D) | Quasi-static and dynamic (1.6 m/s), L-M direction, with flesh and fibula |
Kerrigan et al. 2004 [15] | 19 | 50 % Risk for 50th percentile Male: 312 Nm | Dynamic, L-M direction, with flesh and fibula |
Ivarsson et al. 2005 [16] | 4/4 (distal/proximal loading) | Dynamic, L-M direction, with flesh and fibula |
Loading rate is used as a primary evaluation criterion for previous studies. Some of these studies report results from tests conducted at quasi-static loading rates, which may significantly underestimate the bending tolerance of the femur under impact loading [17, 18]. Carter and Hayes [17] estimated that both strength and modulus of cortical bone were proportional to 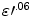 , where
, where 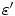 is the strain rate. Additionally, Mather [8] and Martens [19] suggest that bone exhibits an increase in strength and stiffness at higher strain rates during dynamic loading, and Schreiber et al. [12] showed a dramatic difference in bending tolerance of the human leg between quasi-static tests and dynamic tests. While this suggests bone may experience a strain rate sensitivity of fracture tolerance, this effect may be smaller than inter-specimen variation when strain rates vary by less than an order of magnitude. For an order of magnitude estimate, unpublished data from vehicle-pedestrian impact experiments performed using strain gage instrumented PMHS at the University of Virginia suggest that the tibia can experience strain rates from 100 %/s to as high as 700 %/s depending on pedestrian stance and vehicle geometry. Thus, tests where specimens were loaded only quasi-statically, will not be considered in the following review.
is the strain rate. Additionally, Mather [8] and Martens [19] suggest that bone exhibits an increase in strength and stiffness at higher strain rates during dynamic loading, and Schreiber et al. [12] showed a dramatic difference in bending tolerance of the human leg between quasi-static tests and dynamic tests. While this suggests bone may experience a strain rate sensitivity of fracture tolerance, this effect may be smaller than inter-specimen variation when strain rates vary by less than an order of magnitude. For an order of magnitude estimate, unpublished data from vehicle-pedestrian impact experiments performed using strain gage instrumented PMHS at the University of Virginia suggest that the tibia can experience strain rates from 100 %/s to as high as 700 %/s depending on pedestrian stance and vehicle geometry. Thus, tests where specimens were loaded only quasi-statically, will not be considered in the following review.
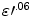 , where
, where 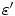 is the strain rate. Additionally, Mather [8] and Martens [19] suggest that bone exhibits an increase in strength and stiffness at higher strain rates during dynamic loading, and Schreiber et al. [12] showed a dramatic difference in bending tolerance of the human leg between quasi-static tests and dynamic tests. While this suggests bone may experience a strain rate sensitivity of fracture tolerance, this effect may be smaller than inter-specimen variation when strain rates vary by less than an order of magnitude. For an order of magnitude estimate, unpublished data from vehicle-pedestrian impact experiments performed using strain gage instrumented PMHS at the University of Virginia suggest that the tibia can experience strain rates from 100 %/s to as high as 700 %/s depending on pedestrian stance and vehicle geometry. Thus, tests where specimens were loaded only quasi-statically, will not be considered in the following review.
is the strain rate. Additionally, Mather [8] and Martens [19] suggest that bone exhibits an increase in strength and stiffness at higher strain rates during dynamic loading, and Schreiber et al. [12] showed a dramatic difference in bending tolerance of the human leg between quasi-static tests and dynamic tests. While this suggests bone may experience a strain rate sensitivity of fracture tolerance, this effect may be smaller than inter-specimen variation when strain rates vary by less than an order of magnitude. For an order of magnitude estimate, unpublished data from vehicle-pedestrian impact experiments performed using strain gage instrumented PMHS at the University of Virginia suggest that the tibia can experience strain rates from 100 %/s to as high as 700 %/s depending on pedestrian stance and vehicle geometry. Thus, tests where specimens were loaded only quasi-statically, will not be considered in the following review.Mather [8] tested a large number of tibiae in dynamic drop testing with different impact energies to determine which proportion of specimens failed at each level of impact energy. No moment or force calculations were made and thus the results of the study cannot be used in the development of injury risk functions.
In Rabl et al. [11], the authors’ goals were to gain basic information on the fracture behavior and fracture morphology of the tibia and to determine the relevance of the results for general practice. Thirty-two human tibiae (16 matched pairs) were loaded in bending, with 8 specimens each loaded on each of the 4 anatomical faces of the bone (posterior, anterior, lateral, and medial). The authors constrained the ends of the bone, which likely influenced the wide range of fracture tolerances presented (2,475–12,206 N). The authors do not report span length or moment data, nor do they report any anthropometrical measurements of the specimens (age, gender, stature, and weight were provided). The specimens were loaded at 0.3 m/s and data was sampled at 600 Hz from an accelerating load cell that was not inertially compensated. Additionally, only 20 cm long sections of tibiae were used, harvested from the specimen 6 cm distal to the tibial plateau regardless of specimen length. Thus, results from their study cannot be used to develop injury risk functions for bending loading of the tibia/fibula/leg. However, interestingly, despite mid-shaft loading of all specimens, the study reports distal third fractures in almost 60 % of the anterior loading cases, as well as in 20 % of cases with medial loading and 20 % of cases with lateral loading.
Almost all of the remaining studies (other than Nyquist et al. [10]) were performed by the University of Virginia [12–16]. Among these studies, only Schreiber et al. [12] presents data for leg bending in the posterior-anterior (P-A) direction, while the rest present data for bending in the lateral-medial (L-M) direction. Studies presenting data on the tolerance of the leg/tibia/fibula under L-M loading will be discussed first, followed by studies discussing the tolerance in P-A direction.
18.2.1.2 Dynamic Bending Tolerance of the Human Leg/Tibia/Fibula Under L-M Loading
In Kerrigan et al. [13], four matched pairs (all male) of leg specimens were loaded in L-M three point bending (Fig. 18.4). The epiphyses of each specimen were potted in rigid potting cups and attached to rollers. The rollers rested on greased support plates to create a simple support boundary condition at each end. The central loading was provided by a padded aluminum ram attached to the actuator of a servohydraulic materials testing machine able to deliver downward displacement pulses at controllable rates as high as 1.6 m/s. Each of the four matched pair bending tests was used to investigate the influence of a particular parameter on the bending strength of the leg/tibia (Table 18.3). In the first two pair of specimens, the influence of location of the central loading point was investigated by comparing the fracture tolerance of the tibia loaded at the mid-shaft versus loading at the proximal third location (first pair), and mid-shaft versus loading at the distal third location (second pair). The distal third and proximal third loading locations were defined by measuring to a point located 33 % of the bone’s length measured from the distal tip of the medial malleolus and from the proximal tip of the tibial spine. The fracture tolerance in bending was slightly higher in proximal third loading than in mid-shaft loading in the first pair, and slightly higher in mid-shaft loading than in distal third loading in the second pair. The effect of rate sensitivity was investigated using the third pair of specimens, both loaded at the proximal third location; however, one was loaded at 0.001 m/s while the other was loaded at the dynamic rate. A larger difference in fracture tolerance was reported in the pair loaded at rate than in either of the loading location pairs. In the fourth pair, one denuded tibia was loaded to failure at the mid-shaft and the other specimen with tissue intact (fibula and surrounding flesh were intact, including proximal and distal tibio-fibular joints). The greatest difference in fracture tolerance was noted in this pair: the denuded tibia failed at a bending moment less than 75 % of the failure moment in the leg segment case. This result highlights the importance of not only validating whole bone bending response of the tibia and fibula, but that the entire leg specimen (tibia, fibula and surrounding flesh) bending tolerance should be as well.
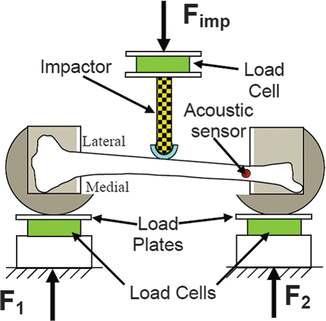

Fig. 18.4
Tibia/leg bending test setup schematic (From the work of Kerrigan et al. 2003a)
Spec. | Impact location | Tibia lengtha (mm) | Mid shaft circum.b (mm) | Span (mm) | Proximal moment arm (mm) | Distal moment arm (mm) | Moment arm ratioc | Summed support loadd (N) | Peak moment (Nm) |
|---|---|---|---|---|---|---|---|---|---|
122 L | Mid diaph. | 385.0 | 320.0 | 343.2 | 172.1 | 171.1 | 1.01 | −3,842 | −333.8 |
122R | Prox 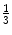 | 385.0 | 320.0 | 337.8 | 102.2 | 235.6 | 0.43 | −4,644 | −342.1 |
140 L | Mid diaph. | 405.0 | 355.0 | 363.4 | 181.7 | 181.7 | 1.00 | −2,656 | −251.7 |
140R | Dist 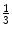 | 410.0 | 355.0 | 325.6 | 222.3 | 103.3 | 2.15 | −2,458 | −224.7 |
150 Le | Prox 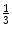 | 405.0 | 390.0 | 352.5 | 113.1 | 239.4 | 0.47 | −3,549 | −283.4 |
150R | Prox 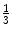 | 390.0 | 390.0 | 351.1 | 108.3 | 242.8 | 0.45 | −4,152 | −329.8 |
134R | Mid diaph. | 418.0 | 290.0 | 368.4 | 182.1 | 186.3 | 0.98 | −3,017 | −301.5 |
134 L | Mid diaph.f | 426.0 | 315.0 | 368.6 | 183.8 | 184.8 | 0.99 | −4,276 | −416.5 |
Mean | 403.0 | 342.0 | 351.3 | −3,574.5 | −310.4 | ||||
SD | 15.3 | 36.5 | 15.3 | −796.7 | −59.5 | ||||
A second study was performed by the University of Virginia [14], where 10 whole leg specimens (tibia, fibula, and surrounding flesh) were loaded in L-M three point bending (Fig. 18.5). This study was performed to highlight the rate sensitivity of the bending tolerance and response of whole leg specimens: six specimens were loaded in dynamic bending at 1.6 m/s, and four specimens were loaded in quasi-static bending. The tests were performed using identical hardware and equipment to those performed in the other University of Virginia study [13]. The bending responses were scaled and used to develop a quasi-static and a dynamic response corridor.
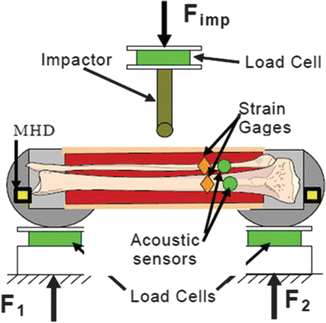

Fig. 18.5
Test diagram for three point bending tests (From the work of Kerrigan et al. 2003b)
In the third University of Virginia study [15], previously published data were combined with data from new experiments in an effort to create an injury risk function for the dynamic L-M bending tolerance of the leg. The new tests presented in this study included four (no matched pairs) leg specimen bending tests performed identically to those presented in the other two Kerrigan et al. [13, 14] studies. The previously published data that were included in the development of the injury risk function were the single leg specimens from Kerrigan et al. [13], the six dynamically loaded leg specimens from Kerrigan et al. [14], and nine tests published by Nyquist et al. [10].
Nyquist et al. [10] performed a series of leg/tibia bending experiments that included nine dynamic (2.1–4.7 m/s) L-M impacts to simply supported leg specimens (with tibia, fibula and surrounding flesh). Nyquist et al. [10] reported that force data were filtered at 100 Hz to “smooth the traces and slightly attenuate the short duration spikes”. Upon examination of the filtered and unfiltered data, it was concluded that the filtered data attenuated the peak forces by approximately 10 %. Nyquist also reported that there was no evidence to suggest that tibial fracture occurs at the peak force, so only filtered values are presented in the paper.
Thus for the purpose of the injury risk function development in Kerrigan et al. [15], all of the data from Nyquist et al. [10] were considered to be right-censored (fracture happens at a force or moment greater than the published values) and data from the other previous University of Virginia studies were to be considered exact, or uncensored (for more information on data censoring or injury risk function development see Kent and Funk [20]). The (moment-based) fracture tolerance of each of the 20 specimens was geometrically scaled to represent the 50th percentile male fracture tolerance using a whole bone length scale factor and 379 mm as the 50th percentile male tibia length. After scaling, 19 of the 20 available data points were used to construct the injury risk function for the leg. One of the Nyquist et al. [10] data points was not used because after scaling the fracture tolerance (634 Nm) was 2.5 standard deviations from the mean of the Nyquist et al. [10] data, 3.2 standard deviations away from the mean of all of the data in Table 18.2, and lastly because it was a right-censored point.
A parametric injury risk curve was developed from a Weibull univariant survival model that was fit to the scaled fracture moment data (8 right censored points and 11 exact points) to determine the relationship between the probability of fracture and peak applied moment. A Weibull model was chosen because it is not necessarily symmetric, permits a zero risk value at zero moment, and has been shown to be no worse than other distributions for modeling biomechanical injury data [20]. The injury risk function for mid shaft L-M bending of the leg is given with 95 % confidence intervals in Fig. 18.6.
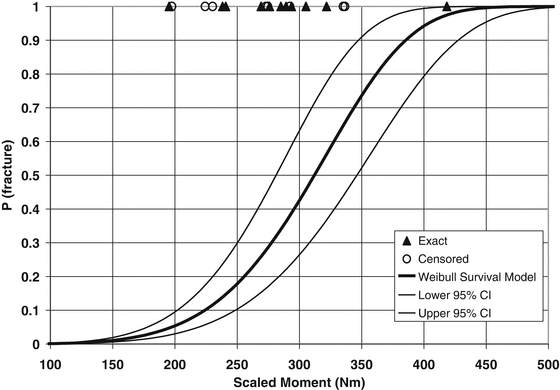

Fig. 18.6
Injury risk function and 95 % confidence interval for the human leg loaded dynamically at the mid shaft in three-point bending (Reproduced with permission from Kerrigan et al. 2004)
In the fourth University of Virginia study [16], the results of eight more dynamic L-M leg (tibia, fibula and surrounding flesh) bending experiments were presented. Four of the specimens were loaded at the distal third location and the remaining four specimens were loaded at the proximal third location. While the scaled (to 50th percentile male) bending tolerance data are presented in this study, no statistical analyses were performed due to the low number of specimens tested in each bending scenario.
In terms of bare bone (tibia or fibula) bending experiments the only available tolerance data for specimens loaded dynamically in the L-M direction were performed by the University of Virginia. However, none of the data have large enough sample sizes to determine injury risk functions with reasonable confidence intervals. Dynamic tolerance for seven bare tibiae loaded in the L-M direction were presented in Kerrigan et al. [13], and the University of Virginia has unpublished data for bending tests performed on the fibulae separated from the tibiae tested for the Kerrigan et al. [13] study. The fibula bending experiments were performed in the L-M direction where matched pairs were used in a manner similar to the tibia tests from Kerrigan et al. [13] to evaluate the influence of loading location and loading rate.
18.2.1.3 Dynamic Bending Tolerance of the Human Leg/Tibia/Fibula Under P-A Loading
Nyquist et al. [10] conducted A-P bending tests on leg specimens in addition to the L-M tests. Nyquist concluded that the tibia failure moment does not depend on the loading direction when comparing A-P bending (avgs. 320 Nm male, 280 Nm female) to L-M bending (avgs. 330 Nm male and 264 Nm female). Despite the shortcomings of the data (see previous section), Nyquist confirmed the earlier finding by Yamada [9] that bending strength was independent of loading direction.
In one study, Schreiber et al. [12] conducted dynamic (5.55 m/s impact velocity) P-A three-point bending tests of the leg complex for 12 intact leg specimens (Table 18.4). For comparison, six additional tests were conducted in A-P direction using identical test conditions (see Ref. [21] and Table 18.4). A Student’s t-test of the P-A and A-P loading scenarios showed no statistically significant differences with a 95 % level of confidence. Crandall et al. [21] concluded that by combining the University of Virginia data with the results of Nyquist et al. [10], the data indicated that the tibia has approximately the same bending moment to failure for all loading directions.
Leg | Energy to failure (J) | Mid-shaft moment (Nm) | Age (years) | Body mass (kg) | Fracture location |
|---|---|---|---|---|---|
Antero-posterior bending [21] | |||||
98-FF-14-RL | 6.73 | 265.28 | 63 | 55.8 | Mid-shaft |
98-FF-7-LL | 6.37 | 341.03 | 72 | 74.8 | Dist. 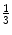 |
98-FF-10-EXT-LL | 12.46 | 340.88 | 86 | 66.2 | Mid-shaft |
98-FF-8-EXT-LL | 11.55 | 425.96 | 77 | 69.4 | Mid-shaft |
98-FF-14-LL | 6.24 | 260.13 | 63 | 55.8 | Mid-shaft |
98-FM-94-RL | 54.27 | 736.64 | 65 | 106.1 | Mid-shaft |
Average | 16.27 | 394.99 | 71.00 | 71.35 | |
Std. dev. | 18.82 | 178.07 | 9.23 | 18.62 | |
Posteroanterior bending [12] | |||||
48-L | 32.4 | 239 | 83 | 61.3 | Mid-shaft |
1004-R | 65.8 | 535 | 59 | 59.9 | Mid-shaft |
1003-R | 67 | 577 | 77 | 69.5 | Mid-shaft |
1000-R | 77.6 | 458 | 85 | 105 | Mid-shaft |
1005-R | 57.9 | 445 | 75 | 73.6 | Mid-shaft |
1006-R | 68.7 | 372 | 70 | 80.4 | Mid-shaft |
1002-R | 55.1 | 259 | 70 | 57.9 | Mid-shaft |
1010-R | 67.3 | 440 | 55 | 73.9 | Mid-shaft |
50-R | 40.2 | 371 | 68 | 46.7 | Dist 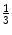 |
68-R | 120.4 | 424 | 56 | 72.6 | Mid and Dist 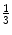 |
69-R | 116.7 | 534 | 62 | 90.3 | Mid and Dist 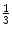 |
73-L | 54.17 | 242 | 61 | 57.2 | Mid-shaft |
Average | 68.61 | 408.00 | 68.42 | 70.69 | |
Std. dev. | 26.48 | 115.48 | 10.13 | 15.97 | |
The concept behind the tibia index comes from classical beam theory that involves a prismatic beam subjected to a combination of bending and compression. The form of the tibia index is closely related to the formula for the response of a beam-column:
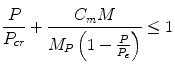
where P is the axial compression force, M is the applied bending moment across the beam, Cm is an empirically derived coefficient, MP is the plastic moment capacity (Mp = σyZP) where σy is the yield strength of that material and ZP is the plastic section modulus. Pcr is the compression capacity of the beam, or Euler load if the slenderness ratio is sufficiently large.
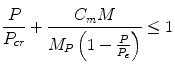
(18.1)
Following the form of this equation, Mertz [22] developed the tibia index as an injury criterion to aid in the design of injury mitigation strategies for lower limb injuries. In this case, the beam-column relation was reworked as the tibia index relation:
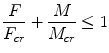
where F is the axial force in the tibia, M is the bending moment in the tibia, and Fcr and Mcr are the critical axial force and bending moment. If the tibia index exceeds the value of 1.0, a tibia injury is predicted.
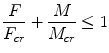
(18.2)
Using tibia properties derived by Yamada [9] and scaling them to different anthropometries, Mertz determined the critical compression force and moments for various occupants (Table 18.5).
Table 18.5
Tibia index critical forces and moments for different anthropometries
Critical value | Small female | Midsize male | Large male |
|---|---|---|---|
Fcr (kN) | 22.9 | 35.9 | 42.2 |
Mcr (Nm) | 115 | 225 | 307 |
Since the introduction of the tibia index to the biomechanics community, one study [12] has evaluated the validity of the criterion for combined axial and bending loads. This study combined a dynamic bending load and a static compression load and produced a decrease in bending moment by 19 % with an averaged scaled failure moment for a 505 male of 372 Nm. This appears to confirm that the interaction of the bending and compression forces combine to affect the fracture tolerance of the tibia.
Crandall et al. [21] reviewed all subsequent failure tests involving the tibia and offered revised tolerance values for the tibia index. Specifically, this review found that axial and bending tolerance for quasi-static loads should be approximately 10.3 kN and 240 Nm, respectively. Assuming that the fibula can handle 10 % of the static axial load of the tibia, the critical static force for the tibia index increases to 11.3 kN. Review of dynamic bending tests suggest a dynamic bending tolerance of 450 Nm. Using the static-to-dynamic scaling presented by Schreiber et al., the dynamic threshold of 16.6 kN is obtained without the fibula, and 18.3 kN with the fibula.
18.2.2 Ankle Injury
As previously noted, axial loading of the ankle complex produces the most serious injuries, but the most frequent injuries (i.e., malleolar fractures) are produced by a number of different mechanisms. Since we could not eliminate any loading modes, we have included a detailed summary of the literature along with recommended studies to be used for model validation.
18.2.2.1 Xversion Injuries
For simplification purposes, the ankle and subtalar joints have been linked in this chapter for the major motions of the hindfoot. Between the talus and calcaneus lies the subtalar joint, which has the primary function of enabling xversion rotation of the hindfoot. A summary of the response and injury data in both quasi-static and dynamic testing is provided.
Quasi-static Xversion Response
Investigations by the automobile safety community are the only studies with great detail on the quasi-static stiffness of the subtalar joint. Kjaersgaard-Anderson et al. [23] reported the range of motion of the human hindfoot for varying degrees of dorsiflexion. Maximum values for the range of motion used were the result of a 1.5 Nm moment. This moment is much lower than the moment expected in the subtalar joint during toepan intrusion. That being the case, a stiffness function for the subtalar joint was derived that contained the data point of Kjaersgaard-Anderson et al. The actual hindfoot resistance to motion in adduction/abduction and Z-axis rotation was assumed to be a parabolic function of the joint angle about the respective axis. The curve used to represent the resistance to joint motion was calculated as a second order polynomial that intersected the 0° – 0 Nm point and the point measured by Kjaersgaard-Anderson et al. (Fig. 18.7). This stiffness function was assumed for all angles of ankle flexion.
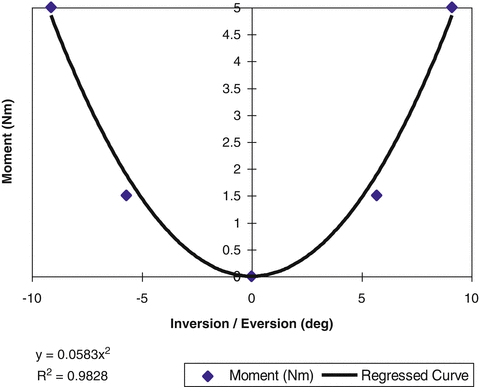

Fig. 18.7
Subtalar joint stiffness curve: inversion/eversion (From the work of Kjaersgaard-Andersen et al. 1988)
More recently, several studies have been performed by researchers in the automobile safety field for development of response corridors and injury thresholds. Parenteau et al. [24] performed quasi-static inversion and eversion tests on 16 cadaver specimens. The calcaneus of each leg specimen was rigidly fixed with screws and the foot was rotated about a fixed anterior-posterior axis. Petit et al. [25] performed quasi-static inversion and eversion tests on 15 cadaver specimens using a test methodology similar to Parenteau et al. [24], but with 400 N of tension applied to the Achilles tendon to simulate emergency braking. Tests were terminated at 45° of rotation, so not all specimens were injured.
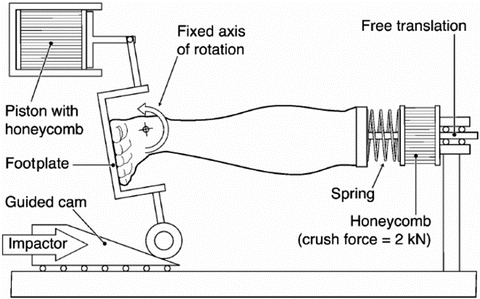
Jaffredo et al. [26] developed a unique test fixture that applied dynamic moments about a prescribed xversion axis. The fixture was developed by the Centre Européen d’Etudes de Sécurité et d’Analyse des Risques (CEESAR) to dynamically (~1,000°/s) apply pure moments about the inversion-eversion axis of the foot through the subtalar joint center. The test apparatus incorporated an adjustable footplate free to rotate about an offset, fixed vertical axis. Rotation of the footplate was driven by a pneumatic impactor striking a guided cam on one side of the plate and controlled by crushable honeycomb inside a piston on the other side (Fig. 18.8).
The striking side of the test apparatus could be reversed to alter the direction of rotation of the footplate. The amount of footplate rotation was prescribed to either 25° or 48° using different sized cams. In some tests, specimens were initially positioned in 14° of inversion or eversion so that a lower (11°) or higher (62°) final level of rotation could be achieved. In a subsequent study, Funk et al. [27] used the CEESAR apparatus and modified the fixture to include initial dorsiflexion and axial loading of the ankle complex. In a real world car crash severe enough to cause injury, the foot/ankle complex may experience significant axial loading and dorsiflexion [28]. These additional loading factors may influence the response, failure strength and injury mode of the foot/ankle complex in inversion and eversion. Thus, Funk et al. [27] attempted to examine the effects of axial preloading and dorsiflexion on the injury tolerance of the human ankle/subtalar joint in dynamic inversion and eversion.
The combined UVA-CEESAR data set consists of 44 tests, including 29 tests conducted at the University of Virginia and 15 tests conducted at CEESAR. Of the 15 CEESAR tests, the 9 non-injury tests were reported by Jaffredo et al. [26]. Given the comparable test apparatus, the results of Jaffredo et al. and Funk et al. appear similar for the case of no axial load or dorsiflexion.
In an effort to summarize the data for FE modeling, composite response graphs for both inversion and xversion have been developed based on all of the available response data and are shown in Figs. 18.9 and 18.10. Since there was a question in terms of the timing of the fracture and the validity of the response beyond the first acoustic burst (potentially denoting fracture), the response curves have been plotted using both the absolute peak moment as well as the moment-angle response until the time of first acoustic burst.
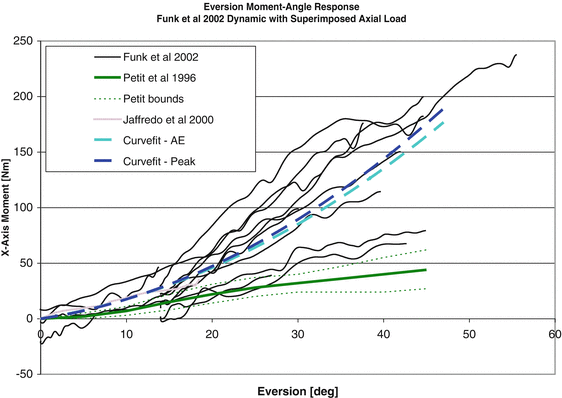
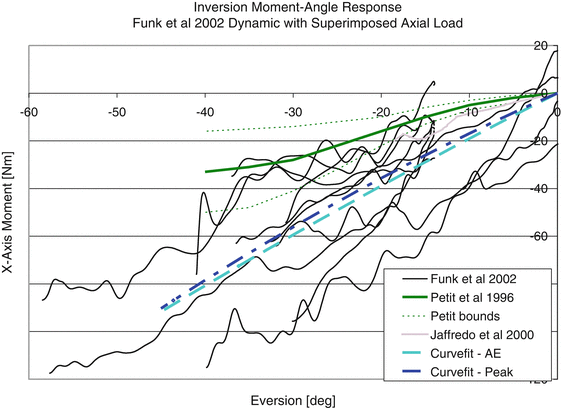

Fig. 18.9
Eversion response showing a comparison of the available quasi-static and dynamic test data

Fig. 18.10
Eversion response showing a comparison of the available quasi-static and dynamic test data
Dynamic Xversion Injury
The tolerance of the ankle/subtalar joint to inversion and eversion loading has been studied, but limited data is available that is appropriate for use in model development and validation. Several investigators have generated ankle injuries experimentally in cadaver specimens to study injury patterns, but have not measured failure strength [29–31]. Begeman et al. [32] performed dynamic inversion and eversion tests on 18 cadaveric leg specimens. A plate was attached to the foot of each specimen and struck by an impactor at an off-axis location 50 mm medial or lateral to the ankle center. The impact generated peak axial loads ranging from 270 to 1,300 N (average = 700 N) as well as a moment about the ankle joint. Ligaments were exposed and stained with a dye so that the time of injury could be determined from high-speed video. Injuries were generated in 13 specimens and consisted primarily of collateral ligament tears and avulsions, as well as 3 malleolar fractures. Peak ankle moments ranged from 9 to 120 Nm, with a mean failure moment of 33 ± 7 Nm in inversion and 41 ± 14 Nm in eversion (Table 18.6). High-speed video revealed that ligaments began tearing before fracture in some tests, but that fracture occurred at the time of peak moment. In spite of this finding, Begeman et al. [32] claimed that peak moment was not a good predictor of injury, and suggested that the best threshold of injury was 60° ± 6° degrees of inversion or eversion, as measured by the rotation of the footplate relative to the tibia. For the Parenteau et al. [24] tests, every test produced injury (primarily collateral ligament tears and avulsions, as well as two malleolar fractures). Failure was defined by audible joint damage or a drop in ankle moment. Inversion failure occurred at 34 ± 15 Nm and 34 ± 8°, and eversion failure occurred at 48 ± 12 Nm and 32 ± 7° (Table 18.6). Specimen age, gender, and bone mineral content were not found to be significant predictors of failure moment or failure angle, except in the case of inversion failure moment, which was significantly lower for females than males. For the tests performed by Petit et al. [25] failure was defined as the first significant drop in the ankle moment-angle curve. Inversion failure occurred in five specimens at 40 ± 26 Nm and 34 ± 8° and eversion failure occurred in five specimens at 35 ± 9 Nm and 32 ± 7° (Table 18.6).
Investigator | Loading conditions | Directions | Sample size | Failure moment (Nm) | Failure angle |
|---|---|---|---|---|---|
Begeman et al. [32] | Dynamic (~2,000°/s) 700 N axial load | Inversion | n = 6 | 33 ± 7 | 61° ± 6° |
Eversion | n = 7 | 41 ± 14 | 59° ± 6° | ||
Parenteau et al. [24] | Quasistatic (~6°/s) No axial load | Inversion | n = 8 | 34 ± 15 | 34° ± 8° |
Eversion | n = 8 | 48 ± 12 | 32° ± 7° | ||
Petit et al. [25] | Quasistatic (~7°/s) 400 N Achilles tension | Inversion | n = 5 | 40 ± 26 | 34° ± 8° |
Eversion | n = 5 | 35 ± 9 | 32° ± 7° |
Funk et al. [33] performed tests under three different loading conditions: neutral flexion with no axial preload, neutral flexion with 2 kN axial preload, and 30° of dorsiflexion with 2 kN axial preload. Forty-four tests were conducted on cadaveric lower limbs, with injury occurring in 30 specimens. Common injuries included malleolar fractures, osteochondral fractures of the talus, fractures of the lateral process of the talus, and collateral ligament tears, depending on the loading configuration (Fig. 18.11). The time of injury was determined either by the peak ankle moment or by a sudden drop in ankle moment that was accompanied by a burst of acoustic emission.
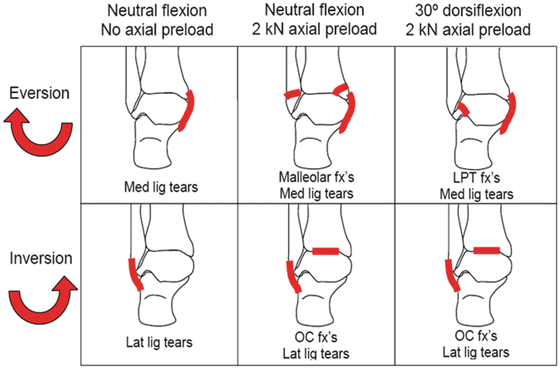

Fig. 18.11
Dependence of xversion injury pattern on the combination of initial position and concomitant axial load [33] (Reproduced with permission from the Stapp Association)
Characteristic moment-angle curves to injury were generated for each loading configuration. Neutrally flexed ankles with no applied axial preload sustained injury at 21 ± 5 Nm and 38° ± 8° in inversion, and 47 ± 21 Nm and 28° ± 4° in eversion. For ankles tested in neutral flexion with 2 kN of axial preload, inversion failure occurred at 77 ± 27 Nm and 40° ± 12°, and eversion failure occurred at 142 ± 100 Nm and 41° ± 14°. Ankles dorsiflexed 30° and axially preloaded to 2 kN sustained inversion injury at 62 ± 31 Nm and 33° ± 4°, and eversion injury at 140 ± 53 Nm and 40° ± 6°.
Survival analyses were performed to generate injury risk curves in terms of joint moment and rotation angle. Rotation direction, dorsiflexion angle, specimen age, gender, mass, height, and BMD were not found to be significant predictors of the angle at injury. However, axial load alone did not model the angle data very well (R2 = 0.16). The following closed-form moment survivor function was generated using only angle and axial load:
![$$ \mathrm{S}\left(\theta \Big|\mathrm{xi}\right)= \exp \left\{- \exp \left[\begin{array}{l}4.88\kern0.24em \cdotp \kern0.24em\ln \left(\theta \right)-\\ {}17.5-0.41\kern0.24em \cdotp\;\\ {}\;\mathrm{Axialload}\;\left(\mathrm{k}\mathrm{N}\right)\end{array}\right]\right\} $$](/wp-content/uploads/2016/09/A31137_3_En_18_Chapter_Equ3.gif)
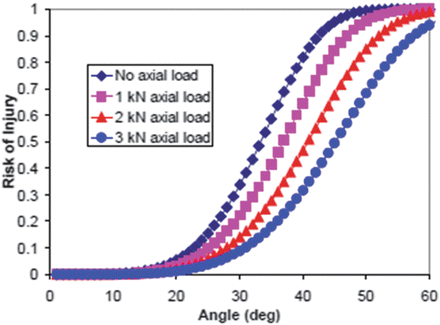
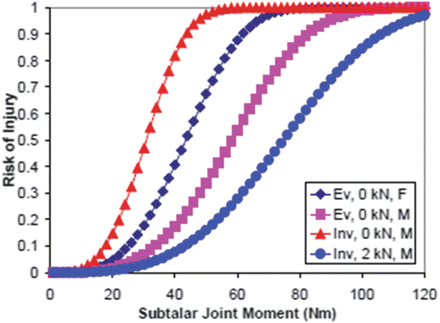
A graphical depiction of the survival function is shown in Fig. 18.12. Since biomechanists will be developing 5th and 95th male and female models, the analysis performed by Funk et al. [33] examining size and gender dependence are also useful for model validation and evaluation. In particular, Funk et al. found a large sensitivity of the response to the age and gender of the specimen (Fig. 18.13).
![$$ \mathrm{S}\left(\theta \Big|\mathrm{xi}\right)= \exp \left\{- \exp \left[\begin{array}{l}4.88\kern0.24em \cdotp \kern0.24em\ln \left(\theta \right)-\\ {}17.5-0.41\kern0.24em \cdotp\;\\ {}\;\mathrm{Axialload}\;\left(\mathrm{k}\mathrm{N}\right)\end{array}\right]\right\} $$](/wp-content/uploads/2016/09/A31137_3_En_18_Chapter_Equ3.gif)
(18.3)

Fig. 18.12
Injury risk as a function of subtalar joint moment for different rotation directions (Ev, Inv), levels of axial preload (1–3 kN) [33] (Reproduced with permission from the Stapp Association)

Fig. 18.13
Injury risk as a function of inversion/eversion angle for different levels of axial preload [33] (Reproduced with permission from the Stapp Association)
18.2.2.2 Dorsiflexion
The more controlled environment of quasi-static tests permitted evaluation of not only the moment-angle characteristics, but also the joint centers of rotation, which were shown to vary slightly with ankle position [24, 25]. Without inertial effects, the results were found to be less variable overall. Petit et al. [25] tested 25 limbs quasi-statically in dorsiflexion with simulated muscle tension applied through the Achilles tendon. The legs were amputated mid-shaft, and the proximal ends of the tibia and fibula were potted together in a cup with cement and Steinmann pins. The calcaneus was potted similarly. In order to apply muscle tension, the Achilles tendon was cut and secured to a cable, which was routed through the test fixture to a counterweight. Dorsiflexion tests were performed with 900 N of tension applied to the Achilles. The prepared specimens were placed in a test fixture which applied rotation to the joint with an electric motor while allowing the specimen to translate in two directions. Of seven legs tested in dorsiflexion, the center of rotation was found to be 76 ± 8 mm proximal from the sole of the foot and 61 ± 6 mm anterior from the posterior face of the heel. The dorsiflexion tests had an average 47 ± 17 N-m and 49° ± 5° failure point. Typical injuries included medial malleolus fractures and calcaneofibular ligament tears.
The quasi-static tests by Parenteau et al. [24] were performed in a fixture similar to the one used by Petit et al. [25], but without the applied muscle tension. Specimen preparation involved cutting the leg mid-shaft and potting the tibia and fibula together in a cup with cement and Steinmann pins. The calcaneus was held with pins and cement in a cup, as well. Torque was applied to the calcaneus cup, which induced rotation in the ankle or subtalar joint, depending on the orientation of the specimen. A motor applied torque at a constant rate of rotation until failure was detected by a drop in moment. Nine tests were performed in dorsiflexion, five of which sustained an injury. Injuries included two lateral malleolus fractures, two calcaneofibular ligament tears and one interosseous talocalcaneal ligament tear. Failure, defined by a drop in moment with increased rotation, occurred at an average moment of 33.1 ± 16.5 N-m and dorsiflexion of 44.0° ± 10.9°, while the average injury moment was 36.2 ± 14.8 N-m with dorsiflexion of 47.0° ± 5.3°. The center of rotation in dorsiflexion was found to be located at the ankle joint, near the center of the talar dome.
Schreiber et al. [34] conducted quasi-static tests in a six-degree of freedom test fixture that was capable of both constrained (rotation about on the dorsiflexion axis) and unconstrained motion. Six cadaveric lower limbs were amputated above the knee and subjected to complete cycles of dorsiflexion and plantarflexion at non-injurious loading levels. For each lower limb, four boundary conditions were used to determine the influence of various below-knee anatomical structures on the ankle response. The ankle test apparatus consisted of a gimbal assembly, with two links centered at the ankle’s theoretical center of rotation. A sprocket, driven by a hydraulic piston at a constant rate, produced a moment in the outermost gimbal assembly aligned with the flexion axis of rotation. As the ankle was forced into flexion, the other axes were unconstrained. The tibia was mounted rigidly to a fixed frame while the foot was mounted to a foot plate fixed to the inner gimbal link. Translation was accommodated by roller bearings in the inner gimbal link. In all, six degrees of freedom (three rotational and three translational), were permitted in the ankle’s motion. The results suggest that dorsiflexion of the ankle is highly dependent on the triceps surae muscle group, the superior tibio-fibular joint, and the relative spacing of the ankle mortise. The insensitivity of plantarflexion motion to varying anatomical conditions suggests that the boney stops, ligaments, and other local anatomical structures determine the extension response.
The overall utility of the tests by Schreiber et al. [34] for FE model validation may lie in the sequential identification of anatomical components to the overall response of the lower limb. Using a range of motion (ROM) defined as the angle achieved when 6 Nm of torque was applied in any direction, Schreiber et al. produced a stiffness mapping with different boundary conditions (Table 18.7).
Table 18.7
ROM for applied 6 Nm torque with differing boundary conditions
Fixed femur | Severed knee | Potted tibia-fibula | Severed fibula | ||
|---|---|---|---|---|---|
Constrained | Dorsiflexion | 4.7 ± 2.4° | 17.5 ± 4.4° | 22.7 ± 1.7° | 24.5 ± 1.4° |
Plantarflexion | 28.3 ± 4.0°
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|