Fig. 5.1
3D ILC system components: (1) unweighing robotic device, (2) surface electrodes on triceps and anterior deltoid, (3) FES module, (4) real-time processor and interface module, (5) PC, (6) monitor displaying task, and (7) operator monitor
In application, the FES electrodes are attached to the patient’s anterior deltoid and triceps muscles in accordance with clinical guidelines and are connected to a FES module that is, in turn, connected to the interface module. The clinical operator uses a graphical user interface (GUI) to enter data and initiate tests necessary for the generation of a suitable reaching task and information required for the FES control law. Once the task is set up, FES control algorithms are calculated automatically using a graphical simulation environment with access to control toolboxes and downloaded to a dedicated single-board controller. The task is displayed using custom-made virtual reality software, whilst the FES based control law simultaneously provides assistive stimulation to enable its accurate completion. The components of the system are next described in detail.
5.1.1 Mechanical Support
Armeo (Hocoma AG, Zurich, Switzerland) is a commercially available upper extremity therapy system that combines a passive arm support with intensive task-oriented exercises presented in a virtual reality environment. The mechanical support alone is used in the research described in this chapter. Each joint is aligned in either the horizontal or vertical plane, which is measured using a resolver. Moreover, whilst the FES laws and other system components developed in this chapter may in principle be applied using any system (passive or robotic) capable of providing support and kinematic information, the movement constraints and kinetic properties imposed influence the dynamic model used.
5.1.2 Biomechanical Dynamic Model
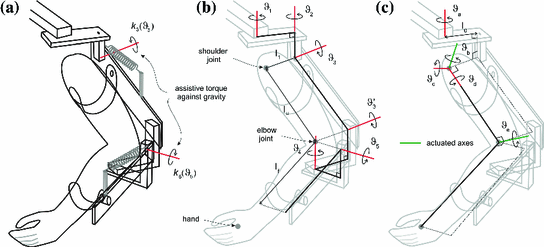
The biomechanical system consists of the human arm and exoskeleton mechanical support system shown in Fig. 5.2a. Figure 5.2b shows the kinematic structure of the exoskeleton support, for which the joint variables are assembled into the vector ![$$q_{a} = [\theta _1, \theta _2, \theta _3, \theta _3', \theta _4, \theta _5 ]^T$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_IEq1.gif) and correspond to the measured joint angles. Also the parallelogram structure of the upper arm section results in
and correspond to the measured joint angles. Also the parallelogram structure of the upper arm section results in 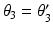 .
.
![$$q_{a} = [\theta _1, \theta _2, \theta _3, \theta _3', \theta _4, \theta _5 ]^T$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_IEq1.gif) and correspond to the measured joint angles. Also the parallelogram structure of the upper arm section results in
and correspond to the measured joint angles. Also the parallelogram structure of the upper arm section results in 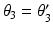 .
.
Fig. 5.2
Kinematic system relationships, a combined system, b Armeo support, and c human arm
Figure 5.2c shows the human arm and since it is strapped to the support there exists a unique bijective transformation between their coordinate sets, given by 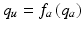 , where
, where
![$$\begin{aligned} q_u = \left[ \vartheta _a, \vartheta _b, \vartheta _c, \vartheta _d, \vartheta _e \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ18.gif) contains the anthropomorphic variables shown in this figure. Using this relationship, application of Lagrangian analysis produces a dynamic model of the combined robotic and human arm systems given in the anthropomorphic coordinates as
contains the anthropomorphic variables shown in this figure. Using this relationship, application of Lagrangian analysis produces a dynamic model of the combined robotic and human arm systems given in the anthropomorphic coordinates as
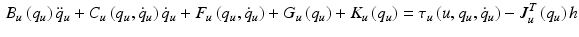
where 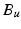 ,
, 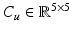 are the inertial and Coriolis matrices, respectively, for the 3D system,
are the inertial and Coriolis matrices, respectively, for the 3D system, 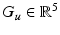 is the vector of moments produced by gravity, and
is the vector of moments produced by gravity, and 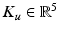 is the vector of moments produced by the unweighing action, where Freeman et al. (2011) gives a full description of the individual components.
is the vector of moments produced by the unweighing action, where Freeman et al. (2011) gives a full description of the individual components.
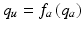 , where
, where![$$\begin{aligned} q_u = \left[ \vartheta _a, \vartheta _b, \vartheta _c, \vartheta _d, \vartheta _e \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ18.gif)
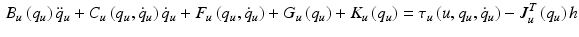
(5.1)
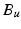 ,
, 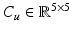 are the inertial and Coriolis matrices, respectively, for the 3D system,
are the inertial and Coriolis matrices, respectively, for the 3D system, 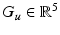 is the vector of moments produced by gravity, and
is the vector of moments produced by gravity, and 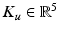 is the vector of moments produced by the unweighing action, where Freeman et al. (2011) gives a full description of the individual components.
is the vector of moments produced by the unweighing action, where Freeman et al. (2011) gives a full description of the individual components.The non-conservative forces assume the same form as in the planar case in the previous chapter and hence
![$$\begin{aligned} F_u \left( q_u, \dot{q}_u \right) = \left[ \begin{array}{ccc} F_a \left( \vartheta _a, \dot{\vartheta }_a \right)&\ldots&F_e \left( \vartheta _e, \dot{\vartheta }_e \right) \end{array} \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ19.gif) whose components incorporate friction and spasticity. Also the vector due to stimulated muscle in (5.1) takes the form
whose components incorporate friction and spasticity. Also the vector due to stimulated muscle in (5.1) takes the form
![$$ \tau _u \left( u, q_u, \dot{q}_u \right) = \left[ \begin{array}{ccccc} 0&\tau _b \left( u_b, \vartheta _b, \dot{\vartheta }_b \right)&0&0&\tau _e \left( u_e, \vartheta _e, \dot{\vartheta }_e \right) \end{array} \right] ^T $$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ20.gif) where
where 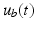 and
and 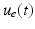 are the electrical stimulation sequences applied to the triceps and anterior deltoid muscles, respectively, and
are the electrical stimulation sequences applied to the triceps and anterior deltoid muscles, respectively, and ![$$u = \left[ u_a, u_b, u_c, u_d, u_e \right] ^T$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_IEq10.gif) . Moreover, h represents a vector of external forces and torques applied by the therapist using a handle mounted on a sensor attached to the robotic support and is only used during identification tests.
. Moreover, h represents a vector of external forces and torques applied by the therapist using a handle mounted on a sensor attached to the robotic support and is only used during identification tests.
![$$\begin{aligned} F_u \left( q_u, \dot{q}_u \right) = \left[ \begin{array}{ccc} F_a \left( \vartheta _a, \dot{\vartheta }_a \right)&\ldots&F_e \left( \vartheta _e, \dot{\vartheta }_e \right) \end{array} \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ19.gif)
![$$ \tau _u \left( u, q_u, \dot{q}_u \right) = \left[ \begin{array}{ccccc} 0&\tau _b \left( u_b, \vartheta _b, \dot{\vartheta }_b \right)&0&0&\tau _e \left( u_e, \vartheta _e, \dot{\vartheta }_e \right) \end{array} \right] ^T $$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ20.gif)
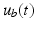 and
and 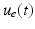 are the electrical stimulation sequences applied to the triceps and anterior deltoid muscles, respectively, and
are the electrical stimulation sequences applied to the triceps and anterior deltoid muscles, respectively, and ![$$u = \left[ u_a, u_b, u_c, u_d, u_e \right] ^T$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_IEq10.gif) . Moreover, h represents a vector of external forces and torques applied by the therapist using a handle mounted on a sensor attached to the robotic support and is only used during identification tests.
. Moreover, h represents a vector of external forces and torques applied by the therapist using a handle mounted on a sensor attached to the robotic support and is only used during identification tests.The model (5.1) is used by the FES control law to calculate a control vector that results in accurate tracking of a reference trajectory. Since assistive torque is applied about the 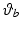 and
and 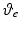 axes only, the system is underactuated. When applied during the treatment of patients, the control law assists tracking about
axes only, the system is underactuated. When applied during the treatment of patients, the control law assists tracking about 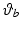 and
and 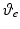 alone, and, in response to clinical guidelines, it is assumed that the patient has sufficient control over the remaining axes to adequately perform the task.
alone, and, in response to clinical guidelines, it is assumed that the patient has sufficient control over the remaining axes to adequately perform the task.
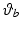 and
and 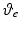 axes only, the system is underactuated. When applied during the treatment of patients, the control law assists tracking about
axes only, the system is underactuated. When applied during the treatment of patients, the control law assists tracking about 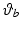 and
and 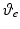 alone, and, in response to clinical guidelines, it is assumed that the patient has sufficient control over the remaining axes to adequately perform the task.
alone, and, in response to clinical guidelines, it is assumed that the patient has sufficient control over the remaining axes to adequately perform the task.5.1.3 FES Module
The FES system can deliver 4 channels of stimulation, each comprising a sequence of bi-phasic pulses at 40 Hz. The frequency, amplitude, pulsewidth range and bi-phasic characteristic have been chosen to achieve a smooth muscle contraction, see de Kroon et al. (2005), McNeal et al. (1986) for a comparison of the effects of the stimulation parameters. The control hardware produces a series of 5 V amplitude, 40 Hz pulses with the required pulsewidth for each channel. Each of them is then optically isolated and fed to the amplification stage of a battery powered commercial stimulator to result in the desired bi-phasic characteristic and voltage amplitude. In response to safety requirements, the pulsewidth and hence the energy supplied to the arm is limited by the control software and by components within the modified stimulator. The amplification level used for each channel is set prior to each treatment session by applying a stimulation signal with pulsewidth 350 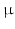 s and then the voltage is slowly increased until the maximum comfortable level is reached.
s and then the voltage is slowly increased until the maximum comfortable level is reached.
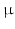 s and then the voltage is slowly increased until the maximum comfortable level is reached.
s and then the voltage is slowly increased until the maximum comfortable level is reached. 5.1.4 Software Systems
In contrast to the planar case of the previous chapter, it is not feasible to display a real world tracking task in 3D and therefore a virtual task is displayed to the patient to ensure clarity, with provision for additional visual instructions and performance feedback. The patient’s screen runs a 3D virtual reality environment that displays a graphic of their arm in real-time, together with the trajectory tracking task, and is shown in Fig. 5.3. The aim of the tracking task is for the patient to follow a sphere that travels along the trajectory at various speeds, whilst ILC laws, designed using the biomechanical system, regulate the assistive FES stimulation required for their completion. The graphic of the patient’s hand changes color to indicate their current error level. Feedback of performance is also given by an error percentage score displayed after each set of trials. A graphic of the initial arm position is displayed to ensure accurate resetting of the system at the start of each trial.
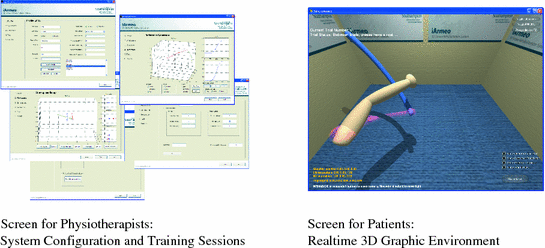

Fig. 5.3
Screen shots of the software system
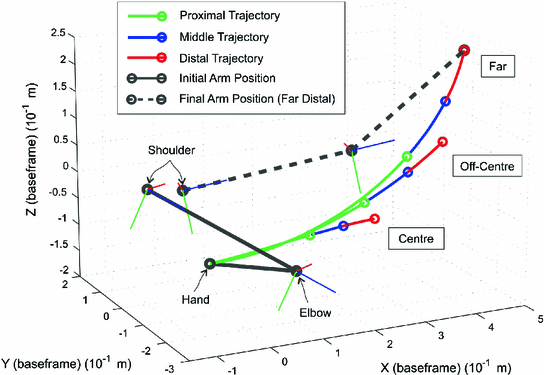
Custom reference trajectories are generated for each patient, producing tracking tasks that extend the arm out in front of the patient in response to clinical need, which were calculated using their identified workspace to establish the maximal arm extension directly in front of them and out to their affected side. By interpolating between these two points a third intermediate point is then generated. Each reference starts from an initial point close to the patient’s body and extends 60, 80 and 100 % of the distance to one of these points. The task comprises reaching out to one of the end-point locations, with the fixed trajectories for each of the five joints generated by scaling a third-order ramp signal of 10 s duration and adding an offset to ensure that it smoothly connects the required start and end joint angles. This results in the vector of reference trajectories
![$$\begin{aligned} q_u^*(t) = \left[ \begin{array}{ccccc} \vartheta _a^*(t)&\vartheta _b^*(t)&\vartheta _c^*(t)&\vartheta _d^*(t)&\vartheta _e^*(t) \end{array} \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ21.gif) where the presence of non-fixed
where the presence of non-fixed 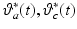 , and
, and 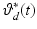 components makes the task more natural to the patients, who can use their remaining voluntary effort to move these joints. An example of the reaching tasks used during testing and in clinical trials is given in Fig. 5.4.
components makes the task more natural to the patients, who can use their remaining voluntary effort to move these joints. An example of the reaching tasks used during testing and in clinical trials is given in Fig. 5.4.
![$$\begin{aligned} q_u^*(t) = \left[ \begin{array}{ccccc} \vartheta _a^*(t)&\vartheta _b^*(t)&\vartheta _c^*(t)&\vartheta _d^*(t)&\vartheta _e^*(t) \end{array} \right] ^T \end{aligned}$$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ21.gif)
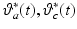 , and
, and 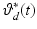 components makes the task more natural to the patients, who can use their remaining voluntary effort to move these joints. An example of the reaching tasks used during testing and in clinical trials is given in Fig. 5.4.
components makes the task more natural to the patients, who can use their remaining voluntary effort to move these joints. An example of the reaching tasks used during testing and in clinical trials is given in Fig. 5.4.
Fig. 5.4
Reference trajectories for the 3D rehabilitation system
5.2 ILC Design
Two ILC designs are used, starting with the phase-lead law of the previous chapter (see also (4.34)),
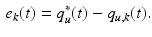
In this 3D case the system is treated as two SISO systems, i.e., the control and movement of forearm and upper arm can be achieved independently of each other. Since FES is applied only about 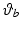 and
and 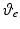 , L is multiplied by the matrix
, L is multiplied by the matrix
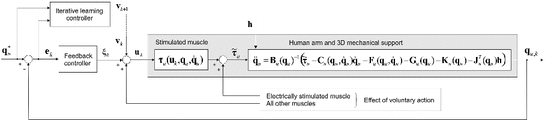
![$$ \left[ \begin{array}{ccccccccc}0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 1 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 1 \end{array} \right] $$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ22.gif) As illustrated in Fig. 5.5, the ILC law operates in conjunction with a feedback controller given by
As illustrated in Fig. 5.5, the ILC law operates in conjunction with a feedback controller given by 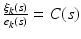 that provides baseline tracking and disturbance rejection. In operation the phase-lead ILC law performs best when the system approximates a simple time-delay and with an appropriately tuned feedback controller can ensure rapid convergence over initial trials. As in the previous chapter, the problem of high frequency components gradually increasing when a large number of trials are performed can always be addressed through use of a zero-phase filter applied to the error or control input, however, the low number of trials performed means that it is unnecessary in the present application. In contrast to phase-lead, Newton ILC (Lin et al. 2006) (2.36)–(2.42) uses the full model in the calculation of the next trial input.
that provides baseline tracking and disturbance rejection. In operation the phase-lead ILC law performs best when the system approximates a simple time-delay and with an appropriately tuned feedback controller can ensure rapid convergence over initial trials. As in the previous chapter, the problem of high frequency components gradually increasing when a large number of trials are performed can always be addressed through use of a zero-phase filter applied to the error or control input, however, the low number of trials performed means that it is unnecessary in the present application. In contrast to phase-lead, Newton ILC (Lin et al. 2006) (2.36)–(2.42) uses the full model in the calculation of the next trial input.
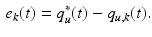
(5.3)
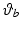 and
and 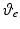 , L is multiplied by the matrix
, L is multiplied by the matrix![$$ \left[ \begin{array}{ccccccccc}0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 1 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 0\\ 0 &{}&{} 0 &{}&{} 0 &{}&{} 0 &{}&{} 1 \end{array} \right] $$](/wp-content/uploads/2016/09/A306304_1_En_5_Chapter_Equ22.gif)
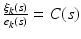 that provides baseline tracking and disturbance rejection. In operation the phase-lead ILC law performs best when the system approximates a simple time-delay and with an appropriately tuned feedback controller can ensure rapid convergence over initial trials. As in the previous chapter, the problem of high frequency components gradually increasing when a large number of trials are performed can always be addressed through use of a zero-phase filter applied to the error or control input, however, the low number of trials performed means that it is unnecessary in the present application. In contrast to phase-lead, Newton ILC (Lin et al. 2006) (2.36)–(2.42) uses the full model in the calculation of the next trial input.
that provides baseline tracking and disturbance rejection. In operation the phase-lead ILC law performs best when the system approximates a simple time-delay and with an appropriately tuned feedback controller can ensure rapid convergence over initial trials. As in the previous chapter, the problem of high frequency components gradually increasing when a large number of trials are performed can always be addressed through use of a zero-phase filter applied to the error or control input, however, the low number of trials performed means that it is unnecessary in the present application. In contrast to phase-lead, Newton ILC (Lin et al. 2006) (2.36)–(2.42) uses the full model in the calculation of the next trial input.
Fig. 5.5
Block diagram representation of the ILC control scheme for the 3D rehabilitation system
5.2.1 Experimental Results with Unimpaired Subjects
The phase-lead and Newton ILC laws were experimentally implemented using six unimpaired participants as an essential step in obtaining ethical approval for patient trials. Representative results and summary statistics are given in this section. Each participant was seated in the robot, which was adjusted to their individual arm dimensions. Electrodes were positioned over their triceps and anterior deltoid muscles in such a way that maximum movement was generated through application of FES. The stimulation amplitude and maximum pulsewidth were adjusted to be within comfortable limits. As described above, the model of the human arm includes two person-dependent parameters that define the position of the anterior deltoid axis, which is fixed with respect to the shoulder as shown in Fig. 5.2c. These were determined before the experiments commenced by applying FES to the anterior deltoid and recording the resulting movements of the human arm. Since the rotation of the human upper arm should then be about the anterior deltoid axis, see Fig. 5.2c, this axis was identified by fitting a plane to the elbow position by least mean squares optimization. The vector perpendicular to the plane, which is also through the pivot, then equates to the required anterior deltoid axis (Freeman et al. 2011).
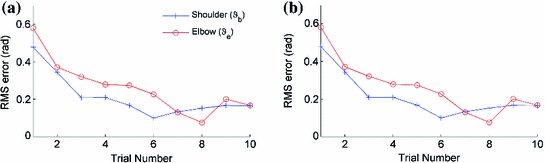

Fig. 5.6
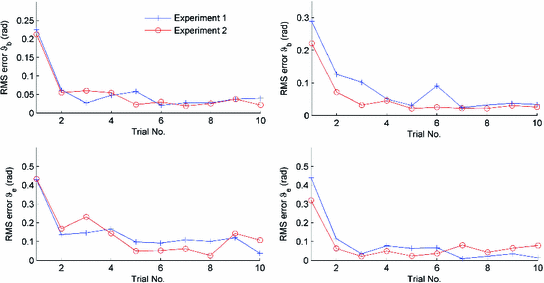
RMS error plots for a participant 1 and b participant 2 using phase-lead ILC
Figure 5.6 gives tracking performance results for two participants with the phase-lead ILC law. The RMS error is given for both 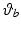 and
and 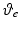 over 10 trials, where for trial k
over 10 trials, where for trial k
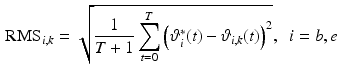
where 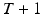 is the number of samples in the discrete representations of the reference
is the number of samples in the discrete representations of the reference 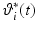 and recorded joint angle sequence
and recorded joint angle sequence 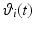 . Due to the kinematic redundancy of the task, this is a more reliable measure than the Cartesian end-point error, which was used in the planar case.
. Due to the kinematic redundancy of the task, this is a more reliable measure than the Cartesian end-point error, which was used in the planar case.
 and
and  over 10 trials, where for trial k
over 10 trials, where for trial k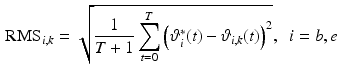
(5.4)
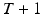 is the number of samples in the discrete representations of the reference
is the number of samples in the discrete representations of the reference 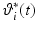 and recorded joint angle sequence
and recorded joint angle sequence 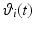 . Due to the kinematic redundancy of the task, this is a more reliable measure than the Cartesian end-point error, which was used in the planar case.
. Due to the kinematic redundancy of the task, this is a more reliable measure than the Cartesian end-point error, which was used in the planar case.
Fig. 5.7
Tracking performance for participant 1 on trial 6. Five second padding is applied at the beginning and end of each reaching movement
In this unimpaired study, the tracking error reduces quickly and maintains a low level as the trials progress. In some cases the RMS error increases slightly in later trials because the participant’s triceps started to suffer from fatigue but the ILC was quickly able to modify the stimulation to maintain a low error. Figure 5.7 shows tracking performance for the same two participants, illustrating close reference tracking for both controlled angles.
Table 5.1 gives summary statistics for 6 unimpaired participants. Each participant undertook ILC trials using two trajectories, the first moved their arm out in front of them and the second moved it out and to their side. The average RMS error was calculated for each trajectory and the mean and standard deviation calculated across participants. These calculations were then repeated using the lowest RMS error recorded for each trajectory.
Table 5.1
Mean (standard deviation) RMS error for 6 unimpaired participants undertaking two trajectory tracking exercises using the 3D robot system with no voluntary assistance
Trajectory 1 | Trajectory 2 | ||
|---|---|---|---|
Shoulder RMS error (rad) | Best trial only | 0.2415 (0.0693) | 0.0574 (0.0557) |
Mean of first 6 trials | 0.0949 (0.0906) | 0.1691 (0.1609) | |
Elbow RMS error (rad) | Best trial only | 0.0721 (0.0700) | 0.0837 (0.0900) |
Mean of first 6 trials | 0.1480 (0.1327) | 0.2189 (0.1723) | |
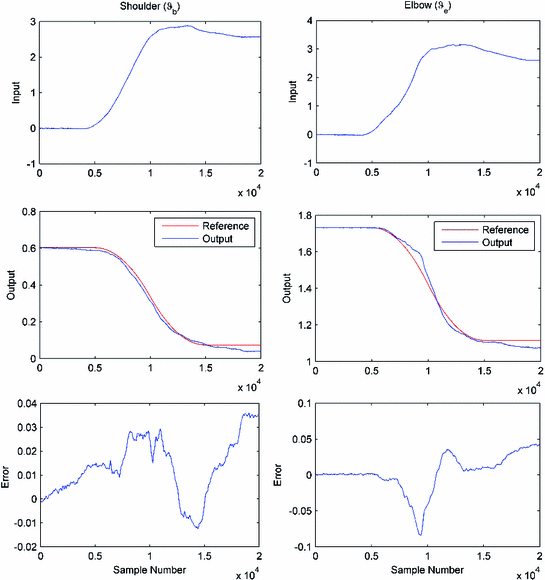
Figure 5.8 shows error norm results over 10 trials of the Newton ILC law for two participants, using a long off-center and a medium off-center trajectory. The results are representative of all the tasks tested and confirm that accurate tracking is achieved within very few trials. The NOILC weighting matrices used in these tests were 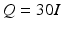 and
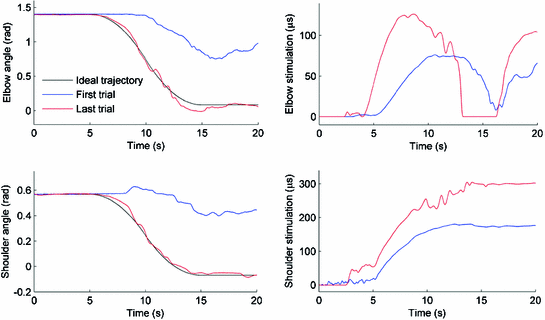
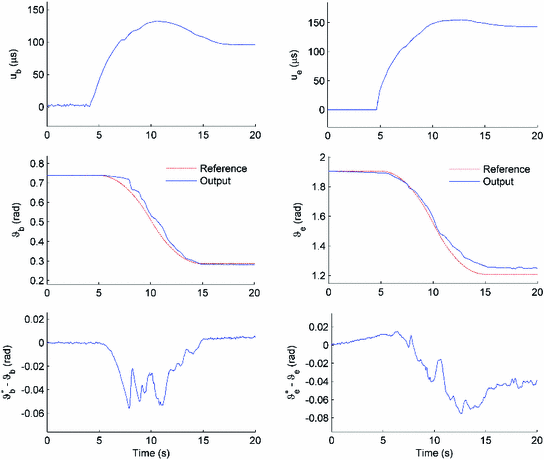
and 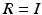 respectively. Figure 5.9 shows representative input, output, and error signals recorded on trial 8 for one participant and confirm that a high level of tracking performance is achieved with an input signal that is not excessive. The theoretical property of monotonic trial-to-trial convergence to zero tracking error is degraded due to inaccuracies in the human arm model, motivating development of more accurate identification procedures, and future use of on-line and recursive techniques. Such identifications routines, however, must be suitable for application within the restrictive conditions of clinical trials, where there is limited set-up time, little opportunity to repeat measurements and satisfactory results for a wide range of patients and changing physiological conditions are required.
respectively. Figure 5.9 shows representative input, output, and error signals recorded on trial 8 for one participant and confirm that a high level of tracking performance is achieved with an input signal that is not excessive. The theoretical property of monotonic trial-to-trial convergence to zero tracking error is degraded due to inaccuracies in the human arm model, motivating development of more accurate identification procedures, and future use of on-line and recursive techniques. Such identifications routines, however, must be suitable for application within the restrictive conditions of clinical trials, where there is limited set-up time, little opportunity to repeat measurements and satisfactory results for a wide range of patients and changing physiological conditions are required.
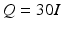 and
and 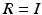 respectively. Figure 5.9 shows representative input, output, and error signals recorded on trial 8 for one participant and confirm that a high level of tracking performance is achieved with an input signal that is not excessive. The theoretical property of monotonic trial-to-trial convergence to zero tracking error is degraded due to inaccuracies in the human arm model, motivating development of more accurate identification procedures, and future use of on-line and recursive techniques. Such identifications routines, however, must be suitable for application within the restrictive conditions of clinical trials, where there is limited set-up time, little opportunity to repeat measurements and satisfactory results for a wide range of patients and changing physiological conditions are required.
respectively. Figure 5.9 shows representative input, output, and error signals recorded on trial 8 for one participant and confirm that a high level of tracking performance is achieved with an input signal that is not excessive. The theoretical property of monotonic trial-to-trial convergence to zero tracking error is degraded due to inaccuracies in the human arm model, motivating development of more accurate identification procedures, and future use of on-line and recursive techniques. Such identifications routines, however, must be suitable for application within the restrictive conditions of clinical trials, where there is limited set-up time, little opportunity to repeat measurements and satisfactory results for a wide range of patients and changing physiological conditions are required.
Fig. 5.8
RMS error plots for 2 participants using Newton ILC, subject 1, left-hand plots, subject 2, right-hand plots
5.2.2 Clinical Trial
The results in this section are, in the main, from Meadmore et al. (2012), which also details how the patients were recruited to the study and ethical approval obtained. On completion of these steps, the five patients chosen (three men and two women) were aged between 33 and 67 years (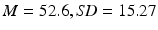 ) and had suffered ischemic strokes, between 6 years 6 months and 11 months prior to recruitment to the study (
) and had suffered ischemic strokes, between 6 years 6 months and 11 months prior to recruitment to the study (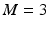 years 10 months,
years 10 months, 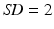 years); four had a hemiparesis of the left side and one of the right. All patients were right-side dominant prior to their stroke and all complied with the study protocol, i.e., attended all sessions. During each intervention session patients spent 40–50 min practising reaching movements.
years); four had a hemiparesis of the left side and one of the right. All patients were right-side dominant prior to their stroke and all complied with the study protocol, i.e., attended all sessions. During each intervention session patients spent 40–50 min practising reaching movements.
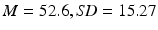 ) and had suffered ischemic strokes, between 6 years 6 months and 11 months prior to recruitment to the study (
) and had suffered ischemic strokes, between 6 years 6 months and 11 months prior to recruitment to the study (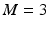 years 10 months,
years 10 months, 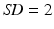 years); four had a hemiparesis of the left side and one of the right. All patients were right-side dominant prior to their stroke and all complied with the study protocol, i.e., attended all sessions. During each intervention session patients spent 40–50 min practising reaching movements.
years); four had a hemiparesis of the left side and one of the right. All patients were right-side dominant prior to their stroke and all complied with the study protocol, i.e., attended all sessions. During each intervention session patients spent 40–50 min practising reaching movements.
Fig. 5.9
Tracking performance of Newton ILC
In advance of the intervention sessions, two assessments, four weeks apart, were completed to establish baseline performance for three clinical outcome measures, with a final assessment one or two days later. Assessments of the upper limb consisted of the FMA and ARAT outcome measures, assessing impairment and function respectively. Eighteen possible reference trajectories were used; each of these could be in one of three orientations relating to space in front and to the hemiplegic side (center, off-center and far), one of three lengths (proximal, middle, and distal) and one of two speeds (5 and 10 s duration).
5.2.3 Unassisted Tracking Tasks
Patients completed four unassisted tracking tasks immediately following set up and at the end of each session. These tasks involved tracking a slowly moving sphere along the far distal, far middle, off-center middle, and center distal trajectories of 10 s duration. Patients attempted each unassisted tracking trajectory once, i.e., each task consisted of one trial, with no FES assistance. For each task, there was a five-second countdown prior to the commencement of each trial, presented both visually and verbally.
One measure of tracking performance that can be compared across different tasks is the RMS of the tracking error, which for joint j is given by (5.4). Once evaluated, this number was divided by the norm of the reference trajectory for the same joint, calculated using the same formula, and the result subtracted from 1. Hence performance score of 1 corresponded to perfect tracking and a negative value indicates a movement away from the desired trajectory.
Assisted tracking tasks were selected according to clinical need and hence some trajectories may have been used more than once or not at all. During each task, FES was applied to the muscles to assist the patient’s tracking. For three of the patients, the triceps and anterior deltoid were trained simultaneously (patients 1, 3, and 5). However, for two patients (2 and 4), an adverse response was observed when both muscles were stimulated, i.e., a flexor synergy was observed, most likely related to spasticity. In these cases, FES was mainly applied to one muscle at time, e.g., stimulation of triceps and then anterior deltoid.
In each task, patients completed 6 trials tracking the same trajectory. A 15 s rest period between trials was designed to reduce fatigue and was extended if necessary. During this period a graphic was presented illustrating tracking performance for the trial just completed and the optimal stimulation signals for application in the next trial were also computed in this time period.
Patients started each movement from the same initial position, which was determined at the start of the first trial and completed between 4 and 6 trials depending on fatigue, where control action to suppress this effect is considered in the next section of this chapter. For each trial tracking performance was measured, as described above, and the percentage of maximum FES applied was calculated by dividing the norm of the FES by the norm of the maximum stimulation that could be applied. Examples of these signals are shown in Fig. 5.10, which also illustrates ILC correcting the applied FES to result in accurate tracking.