to stabilise the system shown in Fig. 3.1 and achieve some level of tracking performance for the controlled joints, 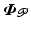 . The resulting closed-loop system [M, K] is represented by
. The resulting closed-loop system [M, K] is represented by
![$$\begin{aligned} G:&\mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{p}_2 [0,T] : \hat{\varvec{\varPhi }} \mapsto \varvec{\varPhi }\nonumber \\&: \left\{ \begin{array}{rl} \underbrace{ \left[ \begin{array}{c} \dot{\varvec{x}}_{s}(t) \\ \dot{\varvec{x}}_{c}(t) \end{array} \right] }_{\displaystyle { \dot{\varvec{x}}(t) }} &{}= \underbrace{ \left[ \begin{array}{c} \varvec{f}_s ( \varvec{x}_{s}(t) ) + \varvec{g}_s ( \varvec{h}_c ( \varvec{x}_{c}(t), \hat{\varvec{\varPhi }}(t) - \varvec{h}_s ( \varvec{x}_{s}(t) ) ) ) \\ \varvec{f}_c ( \varvec{x}_{c}(t), \hat{\varvec{\varPhi }}(t) - \varvec{h}_s ( \varvec{x}_{s}(t) ) ) \end{array} \right] }_{\displaystyle { \varvec{f} ( \varvec{x}(t), \hat{\varvec{\varPhi }}(t) )}} \\ \varvec{\varPhi }(t) &{}= \underbrace{ \varvec{h}_s ( \varvec{x}_{s}(t) ) }_{\displaystyle { \varvec{h} ( \varvec{x}(t) ) }}, \qquad \qquad \qquad \qquad \qquad \qquad \;\;\;\;\; t \in [0,T]. \end{array} \right. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ1.gif)
(4.1)
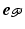 , which can be written in terms of G as
, which can be written in terms of G as 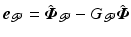 . Here
. Here 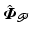 is the reference trajectory, and the following notation extracts the output associated with the controlled joints from operator G:
is the reference trajectory, and the following notation extracts the output associated with the controlled joints from operator G:Lemma 4.1
The relationship between the reference and controlled joints is defined by the map
![$$\begin{aligned} G_{ \mathscr {P}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T] : \hat{\varvec{\varPhi }} \mapsto \varvec{\varPhi }_{ \mathscr {P}} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ2.gif)
with components
![$$\begin{aligned} G_{ \mathscr {P}} \hat{\varvec{\varPhi }} = (G \hat{\varvec{\varPhi }})_{ \mathscr {P}} = \left[ \begin{array}{c} (G \hat{\varvec{\varPhi }})_{\mathscr {P}(1)} \\ \vdots \\ (G \hat{\varvec{\varPhi }})_{\mathscr {P}(n_p)} \end{array} \right] , \;\; (G \hat{\varvec{\varPhi }})_{\mathscr {P}(i)} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}_2 [0,T] : \hat{\varvec{\varPhi }} \mapsto {\phi }_{\mathscr {P}(i)} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ64.gif) and since
and since 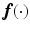 ,
, 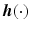 are continuous,
are continuous, 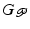 is unique and continuous [13].
is unique and continuous [13].
![$$\begin{aligned} G_{ \mathscr {P}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T] : \hat{\varvec{\varPhi }} \mapsto \varvec{\varPhi }_{ \mathscr {P}} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ2.gif)
(4.2)
![$$\begin{aligned} G_{ \mathscr {P}} \hat{\varvec{\varPhi }} = (G \hat{\varvec{\varPhi }})_{ \mathscr {P}} = \left[ \begin{array}{c} (G \hat{\varvec{\varPhi }})_{\mathscr {P}(1)} \\ \vdots \\ (G \hat{\varvec{\varPhi }})_{\mathscr {P}(n_p)} \end{array} \right] , \;\; (G \hat{\varvec{\varPhi }})_{\mathscr {P}(i)} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}_2 [0,T] : \hat{\varvec{\varPhi }} \mapsto {\phi }_{\mathscr {P}(i)} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ64.gif)
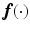 ,
, 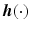 are continuous,
are continuous, 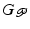 is unique and continuous [13].
is unique and continuous [13].We now add a feedforward signal 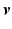 to the previous control scheme, producing the structure shown in Fig. 4.1. Here subscript
to the previous control scheme, producing the structure shown in Fig. 4.1. Here subscript 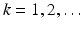 denotes the trial number. Signals
denotes the trial number. Signals ![$$\varvec{v}_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq11.gif) and
and ![$$\varvec{\varPhi }_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq12.gif) are the ILC input and joint angle outputs respectively on the kth trial, and the tracking error on trial k is
are the ILC input and joint angle outputs respectively on the kth trial, and the tracking error on trial k is ![$$\varvec{e}_k = \hat{\varvec{\varPhi }} - \varvec{\varPhi }_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq13.gif) . Note that the analysis which follows can equally be applied to the case where the ILC input is placed between the feedback controller K and the stimulated arm system M, and yields similar results.
. Note that the analysis which follows can equally be applied to the case where the ILC input is placed between the feedback controller K and the stimulated arm system M, and yields similar results.
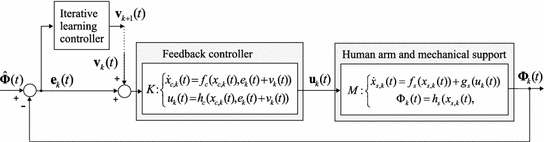
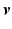 to the previous control scheme, producing the structure shown in Fig. 4.1. Here subscript
to the previous control scheme, producing the structure shown in Fig. 4.1. Here subscript 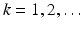 denotes the trial number. Signals
denotes the trial number. Signals ![$$\varvec{v}_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq11.gif) and
and ![$$\varvec{\varPhi }_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq12.gif) are the ILC input and joint angle outputs respectively on the kth trial, and the tracking error on trial k is
are the ILC input and joint angle outputs respectively on the kth trial, and the tracking error on trial k is ![$$\varvec{e}_k = \hat{\varvec{\varPhi }} - \varvec{\varPhi }_k \in \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq13.gif) . Note that the analysis which follows can equally be applied to the case where the ILC input is placed between the feedback controller K and the stimulated arm system M, and yields similar results.
. Note that the analysis which follows can equally be applied to the case where the ILC input is placed between the feedback controller K and the stimulated arm system M, and yields similar results.
Fig. 4.1
ILC scheme added to feedback structure [M, K]
The ILC problem is to ultimately generate a feedforward signal 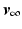 which minimizes the norm of the controlled joint tracking error. This can be stated as:
which minimizes the norm of the controlled joint tracking error. This can be stated as:
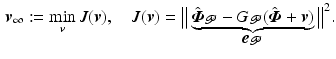
In the ILC framework this problem is solved using iterative optimization methods which employ experimental data to embed robustness against model uncertainty. When the system 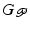 is nonlinear, this can be accomplished using successive linear approximation of the system dynamics, as stated in the following theorem:
is nonlinear, this can be accomplished using successive linear approximation of the system dynamics, as stated in the following theorem:
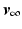 which minimizes the norm of the controlled joint tracking error. This can be stated as:
which minimizes the norm of the controlled joint tracking error. This can be stated as: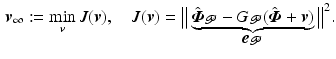
(4.3)
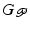 is nonlinear, this can be accomplished using successive linear approximation of the system dynamics, as stated in the following theorem:
is nonlinear, this can be accomplished using successive linear approximation of the system dynamics, as stated in the following theorem:Theorem 4.1
Consider the ILC update sequence
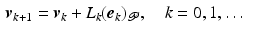
If learning operator ![$$L_k : \mathscr {L}^{n_p}_2 [0,T] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq16.gif) is designed to satisfy
is designed to satisfy
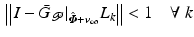
where the operator norm is induced from the inner product  , then
, then
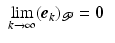
and, for 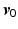 chosen sufficiently close to
chosen sufficiently close to 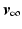 , the ILC update converges to
, the ILC update converges to
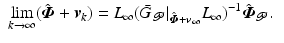
Alternatively, if the learning operator 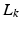 is chosen to satisfy
is chosen to satisfy
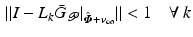
then, for 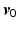 chosen sufficiently close to
chosen sufficiently close to 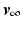 , the ILC update converges to
, the ILC update converges to
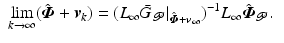
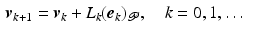
(4.4)
![$$L_k : \mathscr {L}^{n_p}_2 [0,T] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq16.gif) is designed to satisfy
is designed to satisfy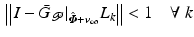
(4.5)
 , then
, then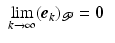
(4.6)
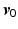 chosen sufficiently close to
chosen sufficiently close to 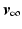 , the ILC update converges to
, the ILC update converges to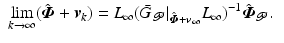
(4.7)
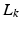 is chosen to satisfy
is chosen to satisfy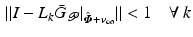
(4.8)
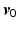 chosen sufficiently close to
chosen sufficiently close to 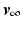 , the ILC update converges to
, the ILC update converges to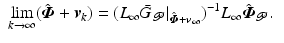
(4.9)
Proof
This result follows from application of conditions in [14] for solving the non-linear equation 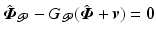 using iterative minimization. In particular, on each iteration the error dynamics locally satisfy
using iterative minimization. In particular, on each iteration the error dynamics locally satisfy
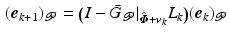
so that, if (4.5) holds, the error converges monotonically to zero since
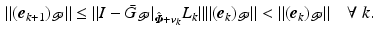 If
If 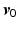 is sufficiently close to
is sufficiently close to 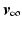 , then
, then 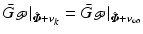 and
and 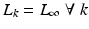 , so that
, so that
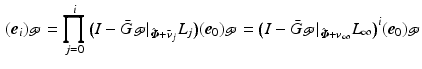
yielding the input expression
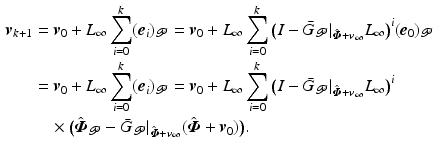
Since we have assumed that (4.5) holds, we have the limit
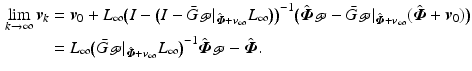
Under the same assumption, we also note that the direct input update sequence is
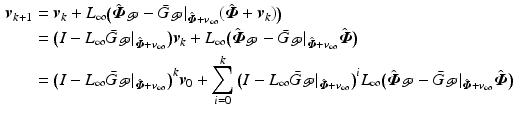
and if (4.8) holds we obtain the limiting input
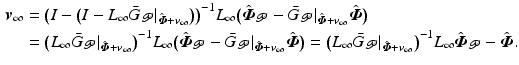 Setting
Setting 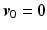 in (4.12) and (4.14) we can also conclude
in (4.12) and (4.14) we can also conclude
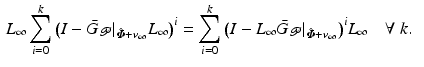

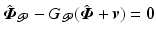 using iterative minimization. In particular, on each iteration the error dynamics locally satisfy
using iterative minimization. In particular, on each iteration the error dynamics locally satisfy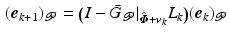
(4.10)
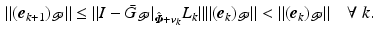
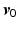 is sufficiently close to
is sufficiently close to  , then
, then 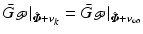 and
and 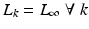 , so that
, so that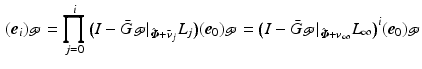
(4.11)
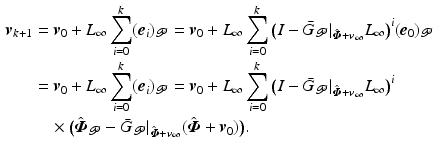
(4.12)
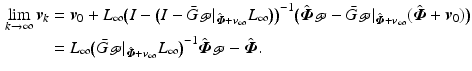
(4.13)
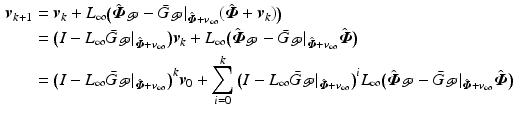
(4.14)
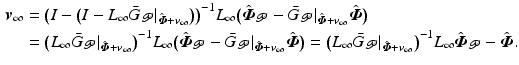
 in (4.12) and (4.14) we can also conclude
in (4.12) and (4.14) we can also conclude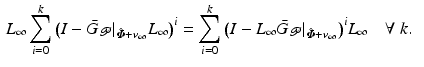
(4.15)

Here ![$$\bar{G}_{ \mathscr {P}} |_{\bar{\varvec{v}}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq30.gif) denotes the system obtained by linearizing
denotes the system obtained by linearizing 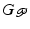 about operating point
about operating point 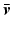 , and can be computed using the following result.
, and can be computed using the following result.
![$$\bar{G}_{ \mathscr {P}} |_{\bar{\varvec{v}}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq30.gif) denotes the system obtained by linearizing
denotes the system obtained by linearizing 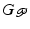 about operating point
about operating point 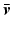 , and can be computed using the following result.
, and can be computed using the following result.Lemma 4.2
Around operating point 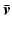 , dynamics
, dynamics 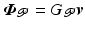 are represented by linear time-varying (LTV) state-space system
are represented by linear time-varying (LTV) state-space system 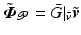 , where
, where
![$$\begin{aligned} \begin{array}{rcl} \dot{\tilde{\varvec{x}}}(t) &{}=&{} A(t) \tilde{\varvec{x}}(t) + B(t) \tilde{\varvec{v}}(t) \\ \tilde{\varvec{\varPhi }}_{ \mathscr {P} }(t) &{}=&{} C(t) \tilde{\varvec{x}}(t), \qquad \qquad \; \tilde{\varvec{x}}(0) = \bar{\varvec{x}}(0), \quad t \in [0,T] \end{array} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ16.gif)
with
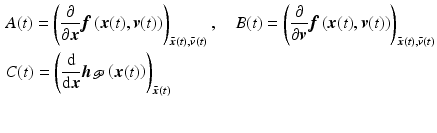
with corresponding map ![$$\bar{G} |_{\bar{\varvec{v}}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq36.gif)
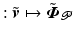 given by
given by
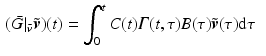 where
where  is the state transition matrix for system (4.16).
is the state transition matrix for system (4.16).
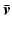 , dynamics
, dynamics 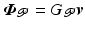 are represented by linear time-varying (LTV) state-space system
are represented by linear time-varying (LTV) state-space system 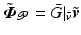 , where
, where![$$\begin{aligned} \begin{array}{rcl} \dot{\tilde{\varvec{x}}}(t) &{}=&{} A(t) \tilde{\varvec{x}}(t) + B(t) \tilde{\varvec{v}}(t) \\ \tilde{\varvec{\varPhi }}_{ \mathscr {P} }(t) &{}=&{} C(t) \tilde{\varvec{x}}(t), \qquad \qquad \; \tilde{\varvec{x}}(0) = \bar{\varvec{x}}(0), \quad t \in [0,T] \end{array} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ16.gif)
(4.16)
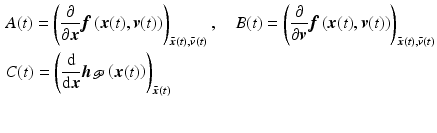
(4.17)
![$$\bar{G} |_{\bar{\varvec{v}}} : \mathscr {L}^{p}_2 [0,T] \rightarrow \mathscr {L}^{n_p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq36.gif)
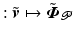 given by
given by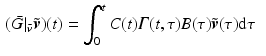
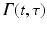 is the state transition matrix for system (4.16).
is the state transition matrix for system (4.16).Depending on the system dynamics and choice of input and output sets, problem (4.3) may have a single or an infinite number of solutions, 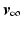 . To examine whether perfect tracking is possible, denote the set of achievable joint motions as
. To examine whether perfect tracking is possible, denote the set of achievable joint motions as
![$$\begin{aligned}&\text {im}( G_{ \mathscr {P}} ) := \left\{ \varvec{y} = G_{ \mathscr {P}} \varvec{x} \; | \; \varvec{x} \in \mathscr {L}^{p}_2[0,T] \right\} . \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ18.gif)
We next show how ILC update operator 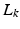 can be chosen to satisfy (4.5) in the case that perfect tracking is possible, or to satisfy (4.8) in the case that it is not.
can be chosen to satisfy (4.5) in the case that perfect tracking is possible, or to satisfy (4.8) in the case that it is not.
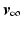 . To examine whether perfect tracking is possible, denote the set of achievable joint motions as
. To examine whether perfect tracking is possible, denote the set of achievable joint motions as![$$\begin{aligned}&\text {im}( G_{ \mathscr {P}} ) := \left\{ \varvec{y} = G_{ \mathscr {P}} \varvec{x} \; | \; \varvec{x} \in \mathscr {L}^{p}_2[0,T] \right\} . \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ18.gif)
(4.18)
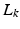 can be chosen to satisfy (4.5) in the case that perfect tracking is possible, or to satisfy (4.8) in the case that it is not.
can be chosen to satisfy (4.5) in the case that perfect tracking is possible, or to satisfy (4.8) in the case that it is not.Theorem 4.2
Within (4.4) let the ILC operator be given by
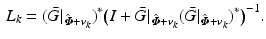
Setting 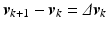 , this is equivalent to solving
, this is equivalent to solving
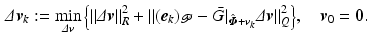
with symmetric positive-definite weights R, Q, and 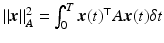 .
.
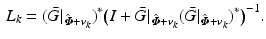
(4.19)
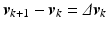 , this is equivalent to solving
, this is equivalent to solving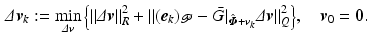
(4.20)
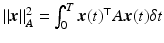 .
.Proof
A necessary condition for local error convergence on trial k is that 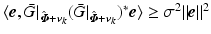 ,
, 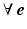 . If
. If ![$$\sigma > 0$$” src=”/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq48.gif”></SPAN> the solution to (<SPAN class=InternalRef><A href=]() 4.20) is then
4.20) is then 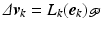 with
with 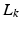 given by (4.19) which satisfies (4.21) since
given by (4.19) which satisfies (4.21) since 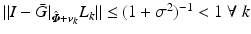 so that
so that 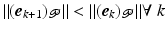 . The limit (4.7) is given by
. The limit (4.7) is given by
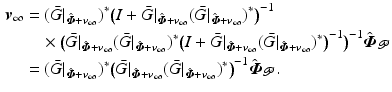
If 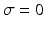 then (4.19), which can also be written as
then (4.19), which can also be written as
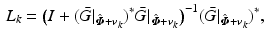
gives 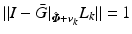 , however if
, however if 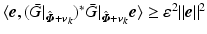 ,
, 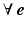 , then
, then
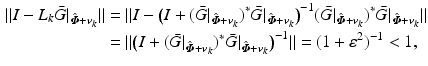 and from (4.14), with
and from (4.14), with 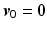 ,
,
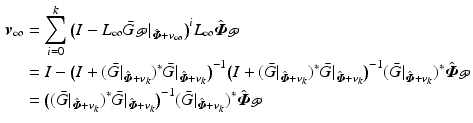
locally satisfying condition (4.22). In (4.19) and (4.24) cases adjoint operator ![$$(\bar{G}|_{\hat{\varvec{\varPhi }} + \varvec{v}_k})^{ *} : \mathscr {L}^{n_p}_2 [0,T] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq59.gif) is given by
is given by
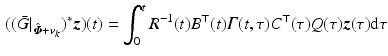 with
with 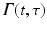 the state transition matrix for state space system
the state transition matrix for state space system 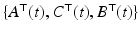 , and hence can be computed efficiently using the adjoint system
, and hence can be computed efficiently using the adjoint system
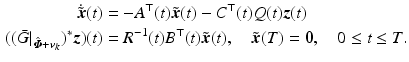

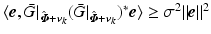 ,
, 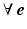 . If
. If 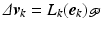 with
with 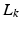 given by (4.19) which satisfies (4.21) since
given by (4.19) which satisfies (4.21) since 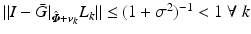 so that
so that 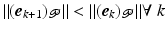 . The limit (4.7) is given by
. The limit (4.7) is given by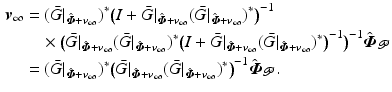
(4.23)
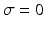 then (4.19), which can also be written as
then (4.19), which can also be written as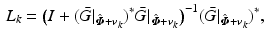
(4.24)
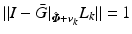 , however if
, however if 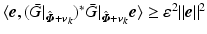 ,
, 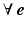 , then
, then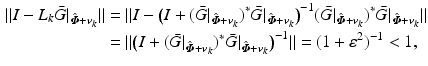
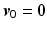 ,
,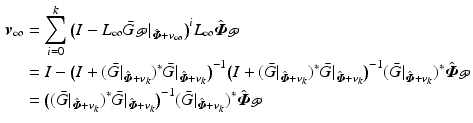
(4.25)
![$$(\bar{G}|_{\hat{\varvec{\varPhi }} + \varvec{v}_k})^{ *} : \mathscr {L}^{n_p}_2 [0,T] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq59.gif) is given by
is given by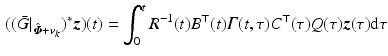
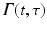 the state transition matrix for state space system
the state transition matrix for state space system 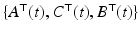 , and hence can be computed efficiently using the adjoint system
, and hence can be computed efficiently using the adjoint system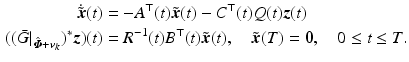
(4.26)

The update of Theorem 4.2 corresponds to the well-known norm optimal ILC update [15–18], and addresses the demands of rehabilitation by allowing the designer to balance change in control input from trial-to-trial and the corresponding error reduction. As more weight is applied to the right-hand term in (4.20), the algorithm corresponds to Newton method based ILC [19], which can be implemented using the simple procedure outlined next:
Lemma 4.3
Choosing 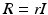 ,
, 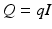 ,
, 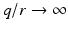 , the ILC update (4.19) realizes minimizing solutions (4.23) or (4.25) respectively in a single iteration. In both cases the required term
, the ILC update (4.19) realizes minimizing solutions (4.23) or (4.25) respectively in a single iteration. In both cases the required term 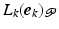 in (4.4) can be efficiently computed off-line between experimental trials as the outcome,
in (4.4) can be efficiently computed off-line between experimental trials as the outcome, 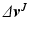 , of J iterations of
, of J iterations of
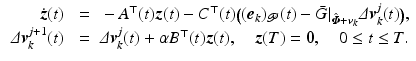
where J and ![$$\alpha > 0$$” src=”/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq68.gif”></SPAN> are sufficiently large and small values respectively.</DIV></DIV><br />
<DIV id=FPar8 class=]()
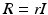 ,
, 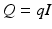 ,
, 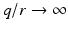 , the ILC update (4.19) realizes minimizing solutions (4.23) or (4.25) respectively in a single iteration. In both cases the required term
, the ILC update (4.19) realizes minimizing solutions (4.23) or (4.25) respectively in a single iteration. In both cases the required term 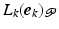 in (4.4) can be efficiently computed off-line between experimental trials as the outcome,
in (4.4) can be efficiently computed off-line between experimental trials as the outcome, 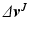 , of J iterations of
, of J iterations of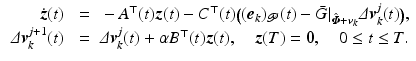
(4.27)
Proof
As 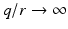 , updates (4.19) and (4.24) respectively converge to
, updates (4.19) and (4.24) respectively converge to
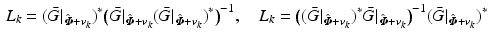 which it is shown in [20] correspond to solutions of the minimum energy problem
which it is shown in [20] correspond to solutions of the minimum energy problem
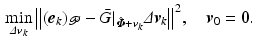
using gradient ILC [21]. This equates to 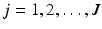 inter-trial iterations of update
inter-trial iterations of update
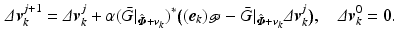
Scalar 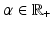 must satisfy
must satisfy 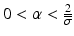 , where
, where 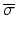 is the smallest
is the smallest 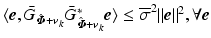 . Using (4.26), update (4.29) yields (4.27).
. Using (4.26), update (4.29) yields (4.27). 
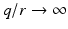 , updates (4.19) and (4.24) respectively converge to
, updates (4.19) and (4.24) respectively converge to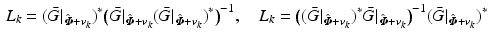
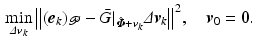
(4.28)
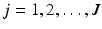 inter-trial iterations of update
inter-trial iterations of update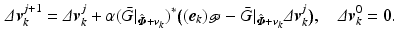
(4.29)
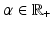 must satisfy
must satisfy 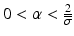 , where
, where 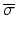 is the smallest
is the smallest 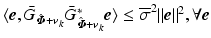 . Using (4.26), update (4.29) yields (4.27).
. Using (4.26), update (4.29) yields (4.27). 
Whatever ILC update operator 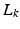 is chosen, bounds on the convergence rate of the approach of Theorem 4.1 follow from properties of iterative minimization techniques established in [14]. These provide an upper bound on the convergence rate as a function of the magnitude of the linearized system, nonlinearity, and proximity of the initial input to the solution. However, these are only valid locally around the operating point of each trial and therefore we will undertake a comprehensive analysis of robustness in Sect. 4.4.
is chosen, bounds on the convergence rate of the approach of Theorem 4.1 follow from properties of iterative minimization techniques established in [14]. These provide an upper bound on the convergence rate as a function of the magnitude of the linearized system, nonlinearity, and proximity of the initial input to the solution. However, these are only valid locally around the operating point of each trial and therefore we will undertake a comprehensive analysis of robustness in Sect. 4.4.
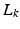 is chosen, bounds on the convergence rate of the approach of Theorem 4.1 follow from properties of iterative minimization techniques established in [14]. These provide an upper bound on the convergence rate as a function of the magnitude of the linearized system, nonlinearity, and proximity of the initial input to the solution. However, these are only valid locally around the operating point of each trial and therefore we will undertake a comprehensive analysis of robustness in Sect. 4.4.
is chosen, bounds on the convergence rate of the approach of Theorem 4.1 follow from properties of iterative minimization techniques established in [14]. These provide an upper bound on the convergence rate as a function of the magnitude of the linearized system, nonlinearity, and proximity of the initial input to the solution. However, these are only valid locally around the operating point of each trial and therefore we will undertake a comprehensive analysis of robustness in Sect. 4.4.The convergence of ILC to a fixed solution, 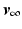 , of problem (4.3), enables us to update our initial stability result of Theorem 3.2 as follows:
, of problem (4.3), enables us to update our initial stability result of Theorem 3.2 as follows:
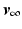 , of problem (4.3), enables us to update our initial stability result of Theorem 3.2 as follows:
, of problem (4.3), enables us to update our initial stability result of Theorem 3.2 as follows:Theorem 4.3
Let ILC operator 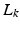 satisfy (4.5). Then the controlled joints converge to reference
satisfy (4.5). Then the controlled joints converge to reference 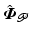 , and the uncontrolled joints are locally stable if Theorem 3.2 is satisfied using operating-point
, and the uncontrolled joints are locally stable if Theorem 3.2 is satisfied using operating-point 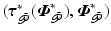
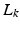 satisfy (4.5). Then the controlled joints converge to reference
satisfy (4.5). Then the controlled joints converge to reference 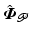 , and the uncontrolled joints are locally stable if Theorem 3.2 is satisfied using operating-point
, and the uncontrolled joints are locally stable if Theorem 3.2 is satisfied using operating-point 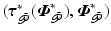
where
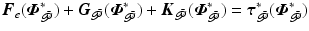 with
with
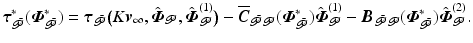
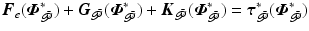
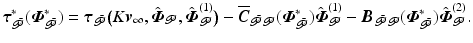
Proof
4.2 Case Study: ILC Applied to Input-Output Linearized System
In the special case that feedback controller K is selected to linearize the system dynamics, the relationship 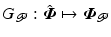 is linear. It follows that system
is linear. It follows that system 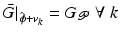 and the properties of Theorem 4.1 hold globally.
and the properties of Theorem 4.1 hold globally.
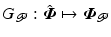 is linear. It follows that system
is linear. It follows that system 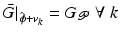 and the properties of Theorem 4.1 hold globally.
and the properties of Theorem 4.1 hold globally.To illustrate this, consider the electrically stimulated, mechanically assisted arm system that was introduced in Sect. 2.2.5, and let feedback controller K be chosen as the input-output linearizing controller of (3.27) developed in Sect. 3.2. About any operating point,  , system
, system 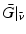 then corresponds to the LTI system given in transfer-function form
then corresponds to the LTI system given in transfer-function form
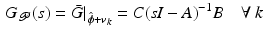
with A, B and C matrices defined by:
![$$\begin{aligned} A&= \left[ \begin{array}{cccc} 0 &{}I &{}0 &{}0 \\ 0 &{}0 &{}I &{}0 \\ 0 &{}0 &{}0 &{}I \\ -A_{0} &{} -A_{1} &{} -A_{2} &{} -A_{3} \end{array} \right] , \quad B = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ A_{0} \end{array} \right] , \quad C = [ \begin{array}{cccc} I&0&\cdots&0 \end{array} ], \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ73.gif) which writing
which writing 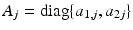 ,
, 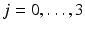 , gives rise to the form
, gives rise to the form
![$$\begin{aligned} G_{ {\mathscr {P}}}(s)&= \left[ \begin{array}{cc} \displaystyle { \frac{a_{10}}{s^4 + a_{13} s^3 + a_{12} s^2 + a_{11} s + a_{10}} } &{}0 \\ 0 &{} \displaystyle { \frac{a_{20}}{s^4 + a_{23} s^3 + a_{22} s^2 + a_{21} s + a_{20}} } \end{array} \right] . \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ74.gif) To design an ILC operator
To design an ILC operator 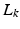 for this system which satisfies (4.5), we will employ Theorem 4.2. This involves minimizing the quadratic objective function of (4.20), which since
for this system which satisfies (4.5), we will employ Theorem 4.2. This involves minimizing the quadratic objective function of (4.20), which since ![$$\left[ \begin{array}{c} (\varvec{e}_{k}(t))_2 \\ (\varvec{e}_{k}(t))_5 \end{array} \right] - G_{ {\mathscr {P}}} \varDelta \varvec{v} = \left[ \begin{array}{c} (\varvec{e}_{k+1}(t))_2 \\ (\varvec{e}_{k+1}(t))_5 \end{array} \right] $$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq91.gif) , specifies in the current case to
, specifies in the current case to
![$$\begin{aligned}&\int _{t = 0}^T \Big \{ ( \varvec{v}_{k+1}(t) - \varvec{v}_k(t) )^\top R ( \varvec{v}_{k+1}(t) - \varvec{v}_k(t) ) \nonumber \\&\qquad \qquad \quad + \big [ (\varvec{e}_{k+1}(t))_2, \; (\varvec{e}_{k+1}(t))_5 \big ] Q \left[ \begin{array}{c} (\varvec{e}_{k+1}(t))_2 \\ (\varvec{e}_{k+1}(t))_5 \end{array} \right] \Big \} dt \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ31.gif)
where T is the duration of the task. Through selection of symmetric positive-definite weighting matrices R and Q, this objective function allows the designer to balance accuracy of task completion with the amount of ES applied to assist the impaired participant’s movement. The solution to minimizing (4.31) is given by (4.19), which specifies in the current case to the update
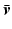 , system
, system 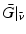 then corresponds to the LTI system given in transfer-function form
then corresponds to the LTI system given in transfer-function form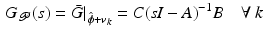
(4.30)
![$$\begin{aligned} A&= \left[ \begin{array}{cccc} 0 &{}I &{}0 &{}0 \\ 0 &{}0 &{}I &{}0 \\ 0 &{}0 &{}0 &{}I \\ -A_{0} &{} -A_{1} &{} -A_{2} &{} -A_{3} \end{array} \right] , \quad B = \left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ A_{0} \end{array} \right] , \quad C = [ \begin{array}{cccc} I&0&\cdots&0 \end{array} ], \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ73.gif)
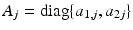 ,
, 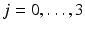 , gives rise to the form
, gives rise to the form![$$\begin{aligned} G_{ {\mathscr {P}}}(s)&= \left[ \begin{array}{cc} \displaystyle { \frac{a_{10}}{s^4 + a_{13} s^3 + a_{12} s^2 + a_{11} s + a_{10}} } &{}0 \\ 0 &{} \displaystyle { \frac{a_{20}}{s^4 + a_{23} s^3 + a_{22} s^2 + a_{21} s + a_{20}} } \end{array} \right] . \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ74.gif)
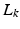 for this system which satisfies (4.5), we will employ Theorem 4.2. This involves minimizing the quadratic objective function of (4.20), which since
for this system which satisfies (4.5), we will employ Theorem 4.2. This involves minimizing the quadratic objective function of (4.20), which since ![$$\left[ \begin{array}{c} (\varvec{e}_{k}(t))_2 \\ (\varvec{e}_{k}(t))_5 \end{array} \right] - G_{ {\mathscr {P}}} \varDelta \varvec{v} = \left[ \begin{array}{c} (\varvec{e}_{k+1}(t))_2 \\ (\varvec{e}_{k+1}(t))_5 \end{array} \right] $$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_IEq91.gif) , specifies in the current case to
, specifies in the current case to![$$\begin{aligned}&\int _{t = 0}^T \Big \{ ( \varvec{v}_{k+1}(t) - \varvec{v}_k(t) )^\top R ( \varvec{v}_{k+1}(t) - \varvec{v}_k(t) ) \nonumber \\&\qquad \qquad \quad + \big [ (\varvec{e}_{k+1}(t))_2, \; (\varvec{e}_{k+1}(t))_5 \big ] Q \left[ \begin{array}{c} (\varvec{e}_{k+1}(t))_2 \\ (\varvec{e}_{k+1}(t))_5 \end{array} \right] \Big \} dt \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ31.gif)
(4.31)

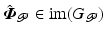
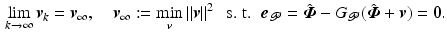
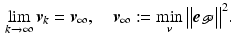
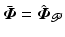

![$$\begin{aligned} \varvec{v}_{k+1} = \varvec{v}_{k} + \underbrace{ G^{*}(s) (I + G(s) G^{*}(s))^{-1} }_{L_k(s)} \overbrace{ \left[ \begin{array}{c} (\varvec{e}_{k})_2 \\ (\varvec{e}_{k})_5 \end{array} \right] }^{(\varvec{e}_k)_{ {\mathscr {P}}}}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_4_Chapter_Equ32.gif)


