Intra- and Inter-person Coordinated Movements of Fingers and Toes

Fig. 4.1

Tasks involving coordinated movements of the right fingers and the right toes. The fingers and the toes simultaneously flex or extend in Simul-Same and Simul-Opp, whereas finger flexion (viz. extension) is coupled with toe extension (viz. flexion) in Alter-Opp and Alter-Same. Fingers and toes rotate in the same direction in Simul-Same and Alter-Same, whereas they rotate in the opposite direction in Alter-Opp and Simul-Opp

In the experimental session, subjects were initially instructed to perform the four tasks several times; each task involved five cycles. This served as a practice session. They were then instructed to perform the tasks at their preferred frequency, but to perform all tasks at the same frequency. We requested that the subjects synchronize the timing of finger peak extension or flexion to toe peak extension or flexion as precisely as possible. The subjects were permitted to choose their preferred range of motion (ROM) of fingers and toes for each task as long as the ROMs differed less than 30 % among the tasks. This was done to minimize the influence of the difference in attentional cost among the tasks in order to maintain a given ROM on the stability of the coordinated movements. After the practice session, the subjects were instructed to perform one of the tasks for 25 cycles, in random order within each cluster of the four tasks. Five clusters were repeated for each subject. Subjects were instructed to not actively resist pattern change and to establish a comfortable pattern. There was no pacing signal such as an auditory metronome during trials.

In experiment 2, ten subjects were initially grouped into five pairs in the order of their average values of movement frequency in experiment 1. Then, across subjects, the pairs of the right hands and feet were made and the subjects performed tasks 1, 2, 3, and 4. Each pair of subjects was seated in a chair, side by side. The subject seated on the right seat put his or her right foot on the incline board and moved their right toes, and the subject seated on the left seat put his or her right forearm on the armrest and moved their right fingers. The subjects were asked to coordinate their periodic movements of toes or fingers to perform tasks 1, 2, 3, or 4 at their preferred frequency. As in experiment 1, the subjects first did a practice session and also decided on movement frequency and ROM in the same way as in experiment 1. The subjects then switched appendages, so the subjects using their right toes used their right fingers and the subjects using their right fingers used their right toes. The tasks were run again. The results of the two combinations were analyzed separately.

4.2.4 Calculation of Relative Phase Between Toes and Fingers Movements

The period of each movement cycle (extension + flexion) of the fingers was compared to the corresponding period of the movement cycle of the toes (extension + flexion in the tasks 1 and 3, or flexion + extension in the tasks 2 and 4). Φ was then calculated as the difference in time between the mid-point of the two periods and expressed in degrees of angular displacement, taking the period of finger movement as a reference. In the present study, the movement cycle of the toes was differently defined for tasks 1 and 3, and for tasks 2 and 4, such that the required Φ was 0° in all tasks. When Φ was less than 90°, we considered the cycle to be successfully performed. When Φ was more than 90°, we considered a loss of stability to have occurred. The standard deviation of Φ (SDΦ) for each trial was calculated using Φ of the first 20 cycles after the intended coordination started or Φ from the beginning of the intended coordination before the occurrence of a loss of stability. The SDΦ was used to represent coordination stability. Trials in which a loss of stability occurred within the first seven cycles after the initiation of the intended coordination were excluded from statistical analysis for the SDΦ calculations. The number of excluded trials was nine in experiment 1 (4.5 % of the total number of trials) and 3 in experiment 2 (1.5 % of the total number of trials).

Movement frequency of the fingers was calculated for each cycle; then mean movement frequency for each trial was calculated using the movement frequency data obtained from the same cycles utilized for the calculation of SDΦ.

4.2.5 Statistics

Differences in SDΦ among the tasks were tested by a two-way ANOVA with repeated measures design (2 × 2, movement coupling × movement direction). The movement coupling condition consisted of two levels: simultaneous flexion of fingers and toes versus alternate flexion of fingers and toes. The movement direction condition consisted of two levels: fingers and toes rotated in the same-direction versus fingers and toes rotated in the opposite-direction. When there was an interaction between movement coupling × movement direction, the Bonferoni test was used to test the difference in SDΦ among the four conditions. Values are presented as means ± SD. Statistical difference was set at a level of p < 0.05.

4.3 Results

In the intra-person coordination of experiment 1, there were significant main effects of both movement coupling (F(1,9) = 15.1, p < 0.005) and movement direction (F(1,9) = 28.6, p < 0.0005) on SDΦ, whereas an interaction between activation coupling × movement direction was not significant (F(1,9) = 0.3, p > 0.05) (Fig. 4.2). SDΦ for each task was in accordance with the number of trials in which a loss of stability occurred (Simul-Same = 2 % (1 trial), Alter-Opp = 30 % (15 trials), Simul-Opp = 10 % (five trials), and Alter-Same = 12 % (six trials), 50 trials for each task).

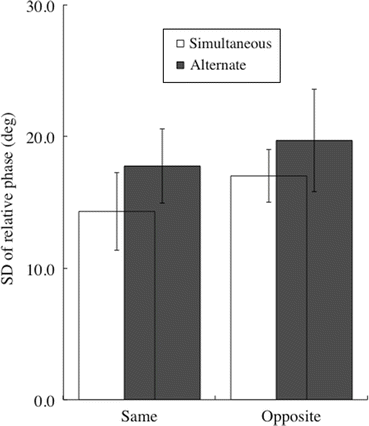
Fig. 4.2

Standard deviation of the relative phase in intra-person coordination. There were significant main effects of both activation coupling (simultaneous versus alternate activation of corresponding muscles of fingers and toes) and movement direction (same- versus opposite-directions). Vertical bars represent SD. N = 10

In the inter-person coordination of experiment 2, there was a significant main effect of movement coupling (F(1,9) = 49.3, p < 0.0001) on SDΦ, though a main effect of movement direction was not significant (F(1,9) = 4.8, p = 0.056). There was a significant interaction between activation coupling × movement direction (F(1,9) = 10.2, p < 0.05) on SDΦ. The Bonferoni test showed that SDΦ in Alter-Opp was significantly greater than that in Simul-Same (p < 0.01), Simul-Opp (p < 0.001), and Alter-Same (p < 0.05), and that there was no significant difference in SDΦ among Simul-Same, Simul-Opp, and Alter-Same (Fig. 4.3). Similar to the case in the intra-person coordination in experiment 1, SDΦ for each task was in accordance with the number of trials in which a loss of stability occurred (Simul-Same = 2 % (one trial), Alter-Opp = 8 % (four trials), Simul-Opp = 4 % (two trials), and Alter-Same = 2 % (one trial), 50 trials for each task), though total number of a loss of stability in the inter-person coordination (eight trials) was smaller than that in the intra-person coordination (27 trials).

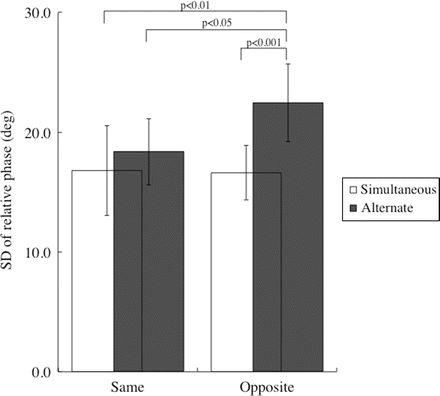
Fig. 4.3

Standard deviation of the relative phase in inter-person coordination. SD of relative phase was significantly greater in Alter-Opp compared to Simul-Same, Simul-Opp, and Alter-Same. Vertical bars represent SD. N = 10

The mean movement frequency in Simul-Same, Alter-Opp, Simul-Opp, and Alter-Same in experiment 1 were 1.15 ± 0.24 Hz, 1.16 ± 0.23 Hz, 1.15 ± 0.23 Hz, and 1.15 ± 0.23 Hz, respectively. The mean movement frequencies in Simul-Same, Alter-Opp, Simul-Opp, and Alter-Same in experiment 2 were 1.32 ± 0.08 Hz, 1.26 ± 0.09 Hz, 1.31 ± 0.09 Hz, and 1.28 ± 0.09 Hz, respectively. Similar values were obtained for the different tasks in each experiment.

4.4 Discussion

The fundamental goal of this study was to investigate whether intra- and inter-person coordination of fingers and toes were constrained based on spatial or motoric information. We measured stability of the coordinated movements of fingers and toes in two modes of coordination with two different forearm positions in order to dissociate influences of spatial and motoric information. The results showed that both relative direction of the movement and activation coupling influenced the stability of coordination to a similar extent in intra-person coordination, and that the coordination with alternate activation of corresponding muscles of fingers and toes in the opposite direction was less stable compared to other coordination modes in inter-person coordination. Consequently, we suggest that both spatial and motoric information are utilized in intra-person coordination of fingers and toes, whereas either spatial or motoric information are utilized in inter-person coordination to meet a specific requirement for each task.

4.4.1 Intra-personal Coordination of Fingers and Toes

The present study showed that both relative direction of the movement and activation coupling influenced the stability of coordination of fingers and toes to a similar extent. It has been shown that bimanual coordination of index finger flexion-extension is predominantly constrained based on motoric relative phase (Riek et al. 1992) and that other coordinated movements of two limbs are predominantly constrained based on spatial relative phase (Baldissera et al. 1982; Carson et al. 1995; Mechsner et al. 2001; Li et al. 2004; Salesse et al. 2005; Muraoka et al. 2013). However, the present study showed that intra-person coordination between toes and fingers was constrained based on both motoric and spatial relative phases independently, which did not agree with previous studies.

The fact that constraint based on motoric relative phase only occurred in coordination between digits flexion/extension in different limbs may be because digit movements are inseparable from functional meaning (i.e., grasping) at the perceptual-cognitive level. On the other hand, the joint movements often utilized in previous studies on intra-person coordination such as flexion/extension of the wrist, elbow, ankle, and knee are not related to specific meaningful behavior. In interlimb coordination of meaningful behavioral patterns, simultaneous execution of meaningful behavior (e.g., simultaneous grasping) could utilize common neural processes for the movements of two limbs and thus would result in more stable coordination compared to alternate execution of meaningful behavioral patterns. On the other hand, when coordinating two limbs movements that normally operate without a specific functional meaning, in terms of the spatial aspects of movements, movements of two limbs in a same direction could utilize a common neural process and thus result in more stable coordination as compared to movements in an opposite direction. We rarely grasp objects using toes in our daily life and our toes are so short that their ability to grasp is limited, and thus the relationship between movement and specific functional meaning might have become less strong for human toe movement. In support of this, the somatic sensibilities for the toes are less than for those of the fingers in humans, while those for the toes and the fingers are almost the same in monkeys, based on studies of evoked potentials in the thalamus and cortex (Kandel 2000). A decline in the toes’ grasping ability in humans might have resulted in the coordination of the fingers and the toes being constrained based on the spatial relative phase as well as the motoric relative phase.

Only gold members can continue reading. Log In or Register to continue