Fig. 9.1
Dynamic human cadaveric ankle loading model in which ankles were made incongruous with a coronally directed osteotomy of the anterior distal tibial surface displaced proximally 2.0 mm (a). Anterior and posterior forces were applied to the tibia through pneumatic cylinders to affect the stability of the joint. Incrementally increasing pulses were applied posteriorly to the tibia (a, black arrow) until subluxation occurred during loading. Changes in contact stress in stable-incongruous and unstable-incongruous specimens were modest compared to intact specimens (b). In contrast, contact stress rates increased dramatically in unstable-incongruous specimens compared to stable-incongruous specimens (b). Contour maps clearly depict relative equivalence in changes in contact stress peaks (c) and significant differences in contact stress rate peaks (d) that occurred during instability
During testing, anteriorly and posteriorly directed forces were applied to the tibia to modulate the sagittal tibiotalar relationship and ultimately the stability of the ankle joint (Fig. 9.1a). Increasing incremental posteriorly directed pulses were applied to the tibia during the gait cycle until the talus grossly subluxated anteriorly into the distal tibial defect during loading. Stresses were captured at a 132 Hz sampling frequency with a pliable piezoelectric real-time stress transducer that was inserted into the ankle joint. Raw data were used to calculate ankle joint contact stress and contact stress rates throughout the motion cycle.
Contact stresses and contact stress rates were compared under metastable conditions within each specimen. Attention was focused on comparing stress measurements between the last cycle in which the talus remained stable beneath the distal tibia (pre-instability cycle termed stable-incongruous) and the first cycle in which the talus subluxated into the distal tibial defect (instability cycle termed unstable-incongruous). Loading conditions were nearly identical between these two tests with identical motion and axial load, and only a 20 N increase in the posteriorly directed impulse applied to the tibia in the unstable-incongruous trial. Therefore, the effects of incongruity with or without instability could be measured.
Peak contact stresses were only 25 % higher in unstable-incongruous specimens compared to stable-incongruous specimens. In contrast, changes in contact stress rates increased 170 % in unstable-incongruous specimens compared to stable-incongruous specimens (Fig. 9.1b). These data clearly depicted the effects of instability. The rapid rise in contact stresses resulting in the increases in contact stress rates occurred over approximately 5 ms and the entire subluxation event lasted approximately 25 ms which was felt to be physiologically relevant. Real-time contact stress and contact stress rate contour plots demonstrate relative equivalence in peak contact stresses in incongruous ankles regardless of instability (Fig. 9.1c). However, the sharp peak in contact stress rate was clearly evident in unstable ankles (Fig. 9.1d). The instability event studied in this experiment was admittedly idiosyncratic. However, the experiment was designed to create conditions in which the talus would subluxate with minimal additional differences in extrinsic loading between stable and unstable conditions allowing the investigators to focus on the mechanical aberrations that occur primarily due to instability in already incongruous joints.
Contact Stress Directional Gradient Changes During Instability
Using an identical cadaveric ankle incongruity/instability model, the effects of incongruity and instability on contact stress directional gradients were determined under metastable conditions [27]. In this experiment, the researchers used regional contact stress measurements to calculate directional stress magnitude vectors (Fig. 9.2a). Peak transient directional gradients nearly doubled in unstable-incongruous specimens compared to intact specimens and increased 50 % in unstable-incongruous specimens compared to stable-incongruous specimens (Fig. 9.2b). Interestingly, under intact conditions, directional gradients were typically randomly oriented throughout the ankle motion cycle at any specific location and low magnitude (Fig. 9.2c left figure). When these individual vectors were summed over the entire motion cycle, the resultant vectors at each locus in intact ankles were close to zero. The authors concluded that small magnitude randomly oriented directional gradient vectors optimized interstitial stresses to maintain homogenous interstitial fluid distribution and healthy chondrocyte mechanotransduction. In contrast, directional gradients were higher in magnitude and preferentially oriented in incongruous specimens and the magnitudes increased significantly secondary to instability (Fig. 9.2c right two figures). Consistent high-magnitude directional gradients with a consistent orientation would increase shearing deformation of regional chondrocytes which has been shown to result in compromised mechanotransduction and cartilage degeneration. Additionally, this type of oriented stress distribution could lead to regions of interstitial fluid depletion.
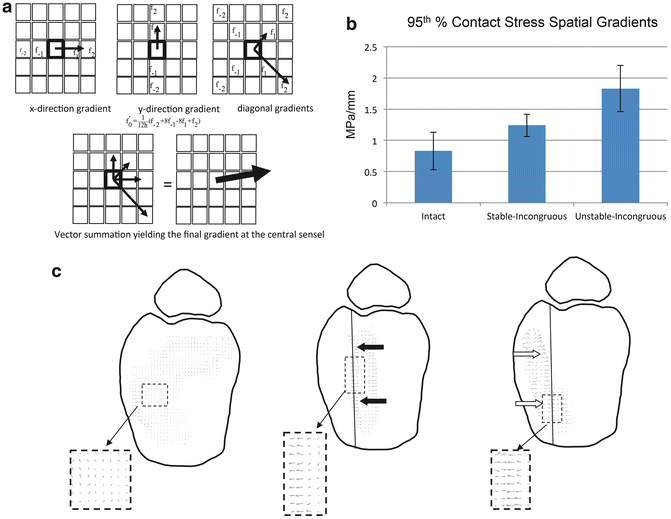

Fig. 9.2
Contact stress directional gradients were calculated by calculating a local derivative at each stress transducer sensel (f0) based on values of neighboring sensels (a). Unstable-incongruous specimens had 100 and 50 % increases in 95th percentile spatial gradient values compared to intact and stable-incongruous conditions (b). Vector plots demonstrate low-magnitude randomly oriented spatial gradients in intact specimens in contrast to polarized higher magnitude vectors in stable-incongruous and unstable-incongruous specimens (c)
In conclusion, human cadaveric testing using an ankle model has been used to develop a physiologically relevant macroscopic model of articular instability. Investigators have created an instability event and quantified resultant changes in articular surface stress transfer. Significant increases in contact stress rates and contact stress directional gradients were documented in incongruous specimens with instability compared to incongruous specimens that remained stable. Typical contact stress rates during instability under these conditions ranged between 100 MPa/s and 200 MPa/s.
Computational Models of Instability
Cadaveric macromechanical models quantify changes in surface stresses allowing measurements of pressure peaks and calculations of time and directional gradients. However, they do not quantify interstitial cartilage stresses and deformations resulting under both normal conditions and under pathologic conditions such as instability and incongruity. Currently, there are limited analyses that allow direct interstitial stress and strain measurements in loaded cartilage. Therefore, investigators have had to rely on computational methods to simulate such information. However, as outlined above, cartilage material properties are complex highlighting the difficulty and ultimately the importance of sophisticated computational methods to accurately simulate interstitial cartilage deformation and stress fields under load.
Goreham-Voss and colleagues developed a transversely isotropic poroelastic finite element model that could simulate unstable motion resulting from an incongruous articulation [28]. This was a two-dimensional model evaluating plane strain and two-dimensional stresses. Initially, the investigators validated the performance of the model by comparing results in congruous and stable ankles to finite element simulations. These comparisons included ankles that were entirely intact and in ankles that had an osteotomy that was anatomically reduced. Subsequently, they modeled a 2.0 mm coronal plane stepoff that simulated cadaveric ankle testing. Under these conditions, they simulated ankle flexion-extension in which the talus remained stable (metastable) under the tibia and conditions in which the talus subluxated anteriorly into the defect (unstable).
Interstitial fluid pressures and stresses increased in metastable and unstable conditions compared to reduced and intact conditions (Fig. 9.3a–c), but the increases were modest. In contrast, temporal gradients of fluid pressure, tangential (shear) stress, and normal stress all increased significantly in unstable conditions compared to metastable conditions. Solid-phase normal transient stress rates increased from approximately 4 MPa/s in metastable conditions to 14 MPa/s in unstable conditions (Fig. 9.3d). Likewise, temporal gradients of solid-phase tangential stresses and fluid pressures increased between 250 % and 300 % in unstable conditions compared to metastable conditions. Incongruity-and instability-related changes in stresses and stress rates were encountered throughout the entire thickness of the cartilage but were greater in the superficial and middle zones of cartilage. These findings demonstrated similar stress rate elevations compared to surface stress rates in cadaveric ankles. In addition, abnormal increases in interstitial stress rates dissipated throughout the thickness of the cartilage demonstrating how cartilage transduces abnormal surface loads to more uniform stresses in the deep layers of cartilage at the level of the subchondral plate.
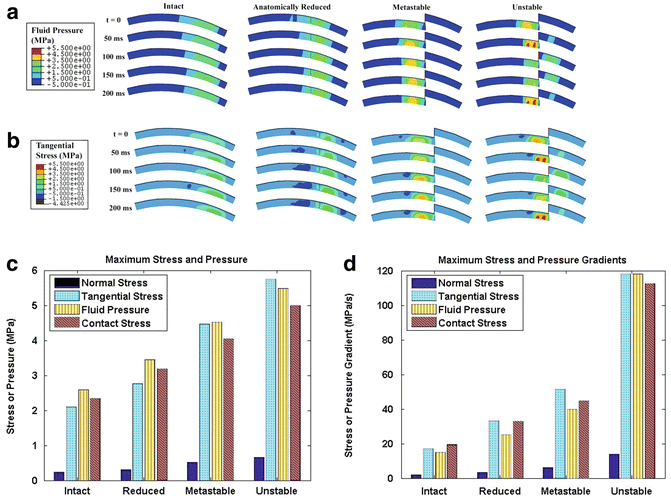

Fig. 9.3
Poroelastic two-dimensional finite element modeling of incongruous and unstable ankle motion demonstrated that both interstitial fluid pressure (a) and solid phase tangential stresses (b) significantly increased secondary to instability during the subluxation event (t = 50 ms) and when the talus reduced back under the distal tibia (t = 200 ms). Fluid pressure, normal stress, and shear (tangential) stress increased modestly in metastable and unstable specimens compared to intact and reduced specimens (c). In contrast, instability resulted in significant increases in temporal gradients of normal stress, shear stress, and fluid pressure compared to metastable, reduced, and intact conditions (d)
Tissue-Level Models of Instability
Cartilage tissue is unique because it exists in vivo in relative anoxia and has no direct blood supply. This allows for explanted tissue-level investigations that can subject cartilage samples to prescribed mechanical perturbations and subsequently measure biosynthetic response under quasi-physiologic conditions.
In an ongoing series of experiments, investigators have subjected freshly explanted bovine tibial plateau osteochondral specimens to a series of repetitive loads. Explants were subjected to loading regimens representing normal loads (1.0 MPa applied at 10 MPa/s) and unstable loads (3 MPa applied at 100 MPa/s) [29]. Specimens were subjected to the prescribed loading regimen for 1,000 cycles at 1 Hz every other day for 2 weeks. In these specimens, materials testing demonstrated that unstable loads resulted in a 20 % increase in compressive modulus and a 20 % decrease in relaxation coefficient compared to normally loaded specimens (Fig. 9.4a). The investigators concluded that short-term exposure to instability type stresses affected the collagenous matrix constituents of cartilage more so than the proteoglycan components. At the end of the testing period, cartilage biosynthesis as measured by proline uptake in specimens subjected to instability loading was 40 % of proline uptake in specimens subjected to normal loads (Fig. 9.4b). In contrast, proteoglycan content was unchanged between the two loading conditions.
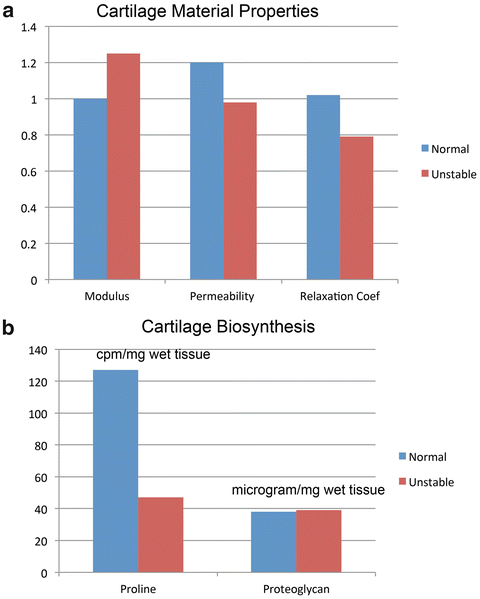

Fig. 9.4
Material property (a) and biochemical (b) changes in osteochondral specimens subjected to normal and unstable loads. Compared to preloading values, instability resulted in a modest rise in compressive modulus and decreases in permeability and relaxation coefficient compared to normally loaded specimens (a). These findings were corroborated in biochemical testing that demonstrated no changes in proteoglycan content but significant decreases in proline uptake consistent with disruption of the collagenous structure of cartilage in unstable specimens (b)
In Vivo Models of Instability
In vitro cadaveric whole-joint mechanical tests yield information regarding changes articular surface stress transfer under pathologic conditions. However, these tests cannot determine tissue-level biologic response to changes in joint loading. Tissue-level testing in freshly harvested specimens has allowed investigators to determine how changes in loading parameters affect the biologic response of viable but isolated cartilage to various injurious loading regimens. However, these tests are reduced to evaluating isolated cartilage biologic responses to mechanical perturbations and cannot account for whole-joint biologic effects of injury. In vivo testing is necessary to truly investigate an organ-level response of a joint to injury or chronic changes in the prevailing loading environment. PTOA is an organ-level disease and ultimately the pathophysiology leading to PTOA needs to be described in survival organ-level investigations. Evidence continues to accumulate describing whole-joint responses to injury, highlighting contributions from cartilage and synovium to mechanical changes in loading.
There have been multiple models of ACL-transection instability used to study articular cartilage changes that result from ligament transaction [30]. Similar alterations of mechanical properties in articular cartilage that are observed in the human with osteoarthritis also occur in the canine after 12 weeks ACL transection [31]. However, rigorous measuring of post-transection instability was not done as a part of this type of investigation. Recently, an in vivo model of joint instability, in which instability was quantified, was developed to investigate the effect of increasing instability on cartilage degeneration and biologic response [32]. In this test, the investigators developed a model of graded instability in rabbit knees to determine the mechanical and biologic effect of instability on an intact joint. Rabbits were subjected to an anterior parapatellar arthrotomy, allowing the anterior cruciate ligament (ACL) to be isolated. Subsequently, graded portions of the ACL were transected. Immediately after transection, the anesthetized rabbits were subjected to sagittal plane translational stability testing using purpose-designed fixturing to quantify the instability resulting from ligament transection. Both the tibia and femur were secured with Steinmann pins which articulated with a custom mechanical actuator that applied a linear displacement to the tibia while the femur was statically stationed. Force/displacement curves were plotted to determine knee stiffness, allowing the investigators to quantify translational kinematics in transaction specimens compared to normal controls. The stiffness of the linear portion of the force displacement curve was a designated surrogate for instability. The laxity encompassing the neutral zone (the “toe” region in the force displacement curve representing normal laxity surrounding the resting position of the ligament around zero displacement) was also quantified. Both the linear stiffness and neutral zone laxity were found to be directly related to the percentage of ACL transaction.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree






