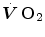Kinetics
Abstract
The steady state of light constant-power submaximal exercise is attained after at least 3 min since the exercise start. Although the application of mechanical power is practically immediate, the rate of oxygen uptake 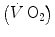 increases at a remarkably slower rate: a metabolic transient phase occurs, during which
increases at a remarkably slower rate: a metabolic transient phase occurs, during which 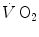 , despite increasing, is insufficient to provide all the metabolic power that is necessary to sustain ATP resynthesis, so that an oxygen deficit is incurred. The oxygen deficit consists of (i) an obligatory component, covered by phosphocreatine breakdown, reflecting the kinetics of glycolysis activation in the contracting muscles, and characterized by an invariant time constant independent of the exercise intensity and (ii) a facultative component, covered by anaerobic lactic metabolism (early lactate accumulation), due to the dissociation between cardiopulmonary response and muscular response at elevated powers, and characterized by a time constant depending on the exercise intensity. The kinetics of
, despite increasing, is insufficient to provide all the metabolic power that is necessary to sustain ATP resynthesis, so that an oxygen deficit is incurred. The oxygen deficit consists of (i) an obligatory component, covered by phosphocreatine breakdown, reflecting the kinetics of glycolysis activation in the contracting muscles, and characterized by an invariant time constant independent of the exercise intensity and (ii) a facultative component, covered by anaerobic lactic metabolism (early lactate accumulation), due to the dissociation between cardiopulmonary response and muscular response at elevated powers, and characterized by a time constant depending on the exercise intensity. The kinetics of 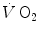 upon exercise onset is described with exponential equations. The implications of single- and double-exponential models are discussed. The former model carries along the assumption that the kinetics of
upon exercise onset is described with exponential equations. The implications of single- and double-exponential models are discussed. The former model carries along the assumption that the kinetics of 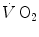 determined at the mouth reflects the kinetics of
determined at the mouth reflects the kinetics of 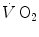 in the contracting muscles. This correspondence, however, does not hold anymore when early lactate appears. The latter model, in particular, implies a rapid phase (phase I), which has been related to the fast cardiovascular responses at exercise start. A single-exponential model assumes also that the exercising muscles behave as dynamic linear first-order systems that, as such, admit only one transfer function. On this basis, ramp exercise and sinusoidal exercise, typically two unsteady-state conditions, are discussed. More recently, at powers higher than the critical power (see Chap. 5), the so-called slow component, or third phase of the
in the contracting muscles. This correspondence, however, does not hold anymore when early lactate appears. The latter model, in particular, implies a rapid phase (phase I), which has been related to the fast cardiovascular responses at exercise start. A single-exponential model assumes also that the exercising muscles behave as dynamic linear first-order systems that, as such, admit only one transfer function. On this basis, ramp exercise and sinusoidal exercise, typically two unsteady-state conditions, are discussed. More recently, at powers higher than the critical power (see Chap. 5), the so-called slow component, or third phase of the 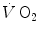 kinetics, has been also characterized. The energetic meaning of the slow component is also discussed. Finally, some methodological aspects of single-breath analysis of pulmonary gas exchange are discussed.
kinetics, has been also characterized. The energetic meaning of the slow component is also discussed. Finally, some methodological aspects of single-breath analysis of pulmonary gas exchange are discussed.
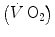 increases at a remarkably slower rate: a metabolic transient phase occurs, during which
increases at a remarkably slower rate: a metabolic transient phase occurs, during which 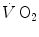 , despite increasing, is insufficient to provide all the metabolic power that is necessary to sustain ATP resynthesis, so that an oxygen deficit is incurred. The oxygen deficit consists of (i) an obligatory component, covered by phosphocreatine breakdown, reflecting the kinetics of glycolysis activation in the contracting muscles, and characterized by an invariant time constant independent of the exercise intensity and (ii) a facultative component, covered by anaerobic lactic metabolism (early lactate accumulation), due to the dissociation between cardiopulmonary response and muscular response at elevated powers, and characterized by a time constant depending on the exercise intensity. The kinetics of
, despite increasing, is insufficient to provide all the metabolic power that is necessary to sustain ATP resynthesis, so that an oxygen deficit is incurred. The oxygen deficit consists of (i) an obligatory component, covered by phosphocreatine breakdown, reflecting the kinetics of glycolysis activation in the contracting muscles, and characterized by an invariant time constant independent of the exercise intensity and (ii) a facultative component, covered by anaerobic lactic metabolism (early lactate accumulation), due to the dissociation between cardiopulmonary response and muscular response at elevated powers, and characterized by a time constant depending on the exercise intensity. The kinetics of 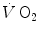 upon exercise onset is described with exponential equations. The implications of single- and double-exponential models are discussed. The former model carries along the assumption that the kinetics of
upon exercise onset is described with exponential equations. The implications of single- and double-exponential models are discussed. The former model carries along the assumption that the kinetics of 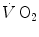 determined at the mouth reflects the kinetics of
determined at the mouth reflects the kinetics of 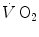 in the contracting muscles. This correspondence, however, does not hold anymore when early lactate appears. The latter model, in particular, implies a rapid phase (phase I), which has been related to the fast cardiovascular responses at exercise start. A single-exponential model assumes also that the exercising muscles behave as dynamic linear first-order systems that, as such, admit only one transfer function. On this basis, ramp exercise and sinusoidal exercise, typically two unsteady-state conditions, are discussed. More recently, at powers higher than the critical power (see Chap. 5), the so-called slow component, or third phase of the
in the contracting muscles. This correspondence, however, does not hold anymore when early lactate appears. The latter model, in particular, implies a rapid phase (phase I), which has been related to the fast cardiovascular responses at exercise start. A single-exponential model assumes also that the exercising muscles behave as dynamic linear first-order systems that, as such, admit only one transfer function. On this basis, ramp exercise and sinusoidal exercise, typically two unsteady-state conditions, are discussed. More recently, at powers higher than the critical power (see Chap. 5), the so-called slow component, or third phase of the 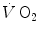 kinetics, has been also characterized. The energetic meaning of the slow component is also discussed. Finally, some methodological aspects of single-breath analysis of pulmonary gas exchange are discussed.
kinetics, has been also characterized. The energetic meaning of the slow component is also discussed. Finally, some methodological aspects of single-breath analysis of pulmonary gas exchange are discussed.Introduction
The steady state of light constant-power submaximal exercise, which I discussed in Chap. 2, is attained after at least 3 min since the exercise start. Although the application of mechanical power is practically immediate, the rate of oxygen uptake or consumption 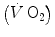 , which at the steady state represents the overall metabolic power, increases at a remarkably slower rate, as when charging a capacitance: a metabolic transient phase occurs before the attainment of the steady state, during which
, which at the steady state represents the overall metabolic power, increases at a remarkably slower rate, as when charging a capacitance: a metabolic transient phase occurs before the attainment of the steady state, during which 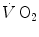 , despite increasing, is insufficient to provide the metabolic power that is necessary to sustain ATP resynthesis at a rate corresponding to that of ATP hydrolysis supporting muscular contraction. As a consequence, during the transient, metabolic power must be generated also by anaerobic metabolism, coherently with Eq. (2.1) (see Chap. 2).
, despite increasing, is insufficient to provide the metabolic power that is necessary to sustain ATP resynthesis at a rate corresponding to that of ATP hydrolysis supporting muscular contraction. As a consequence, during the transient, metabolic power must be generated also by anaerobic metabolism, coherently with Eq. (2.1) (see Chap. 2).
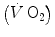 , which at the steady state represents the overall metabolic power, increases at a remarkably slower rate, as when charging a capacitance: a metabolic transient phase occurs before the attainment of the steady state, during which
, which at the steady state represents the overall metabolic power, increases at a remarkably slower rate, as when charging a capacitance: a metabolic transient phase occurs before the attainment of the steady state, during which 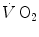 , despite increasing, is insufficient to provide the metabolic power that is necessary to sustain ATP resynthesis at a rate corresponding to that of ATP hydrolysis supporting muscular contraction. As a consequence, during the transient, metabolic power must be generated also by anaerobic metabolism, coherently with Eq. (2.1) (see Chap. 2).
, despite increasing, is insufficient to provide the metabolic power that is necessary to sustain ATP resynthesis at a rate corresponding to that of ATP hydrolysis supporting muscular contraction. As a consequence, during the transient, metabolic power must be generated also by anaerobic metabolism, coherently with Eq. (2.1) (see Chap. 2).The historical view of the kinetics of 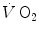 increase upon exercise onset was discussed in Chap. 1 and is summarized in Eq. (1.4), which describes the time course of
increase upon exercise onset was discussed in Chap. 1 and is summarized in Eq. (1.4), which describes the time course of 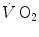 increase as a mono-exponential. This led to the creation of the concept of oxygen deficit, defined as the time integral of Eq. (1.4a). The oxygen deficit corresponds to the amount of metabolic energy that is derived from energy sources other than
increase as a mono-exponential. This led to the creation of the concept of oxygen deficit, defined as the time integral of Eq. (1.4a). The oxygen deficit corresponds to the amount of metabolic energy that is derived from energy sources other than 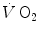 during the exercise transient. An implicit assumption underlies this mono-exponential model of the
during the exercise transient. An implicit assumption underlies this mono-exponential model of the 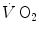 —on kinetics of square wave constant-load exercise: the kinetics of
—on kinetics of square wave constant-load exercise: the kinetics of 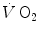 as measured at the mouth corresponds to the kinetics of
as measured at the mouth corresponds to the kinetics of 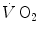 taking place in the working muscles, once possible changes in blood oxygen stores have been accounted for. This assumption implies equal time constants of
taking place in the working muscles, once possible changes in blood oxygen stores have been accounted for. This assumption implies equal time constants of 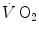 increase at any level in the respiratory system, so that the time constant of
increase at any level in the respiratory system, so that the time constant of 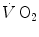 is equal to that of muscle oxygen consumption, or of its mirror image, muscle phosphocreatine decrease. A second fundamental assumption is that the muscle metabolic response to exercise start follows the laws of linear first-order systems. Although this may indeed be the case during light exercise, it is definitely not so during higher intensity exercise.
is equal to that of muscle oxygen consumption, or of its mirror image, muscle phosphocreatine decrease. A second fundamental assumption is that the muscle metabolic response to exercise start follows the laws of linear first-order systems. Although this may indeed be the case during light exercise, it is definitely not so during higher intensity exercise.
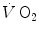 increase upon exercise onset was discussed in Chap. 1 and is summarized in Eq. (1.4), which describes the time course of
increase upon exercise onset was discussed in Chap. 1 and is summarized in Eq. (1.4), which describes the time course of 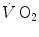 increase as a mono-exponential. This led to the creation of the concept of oxygen deficit, defined as the time integral of Eq. (1.4a). The oxygen deficit corresponds to the amount of metabolic energy that is derived from energy sources other than
increase as a mono-exponential. This led to the creation of the concept of oxygen deficit, defined as the time integral of Eq. (1.4a). The oxygen deficit corresponds to the amount of metabolic energy that is derived from energy sources other than 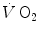 during the exercise transient. An implicit assumption underlies this mono-exponential model of the
during the exercise transient. An implicit assumption underlies this mono-exponential model of the 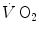 —on kinetics of square wave constant-load exercise: the kinetics of
—on kinetics of square wave constant-load exercise: the kinetics of 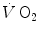 as measured at the mouth corresponds to the kinetics of
as measured at the mouth corresponds to the kinetics of 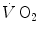 taking place in the working muscles, once possible changes in blood oxygen stores have been accounted for. This assumption implies equal time constants of
taking place in the working muscles, once possible changes in blood oxygen stores have been accounted for. This assumption implies equal time constants of 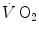 increase at any level in the respiratory system, so that the time constant of
increase at any level in the respiratory system, so that the time constant of 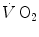 is equal to that of muscle oxygen consumption, or of its mirror image, muscle phosphocreatine decrease. A second fundamental assumption is that the muscle metabolic response to exercise start follows the laws of linear first-order systems. Although this may indeed be the case during light exercise, it is definitely not so during higher intensity exercise.
is equal to that of muscle oxygen consumption, or of its mirror image, muscle phosphocreatine decrease. A second fundamental assumption is that the muscle metabolic response to exercise start follows the laws of linear first-order systems. Although this may indeed be the case during light exercise, it is definitely not so during higher intensity exercise.Soon afterwards, however, it became evident that a single-exponential model was insufficient for a satisfactory description of the 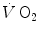 response during the square wave exercise transient. Wasserman et al. (1974) were the first to realize that there might be a rapid component in the earliest phase of the exercise transient, which they attributed to a sudden increase in cardiac output
response during the square wave exercise transient. Wasserman et al. (1974) were the first to realize that there might be a rapid component in the earliest phase of the exercise transient, which they attributed to a sudden increase in cardiac output  . This rapid component became a preferential object of research in the field ever since, particularly by the British school led by Brian Whipp. It was integrated in the subsequent double-exponential model of the exercise transient, proposed by Barstow and Molé (1987). It also restricted the domain of application of the concept of a correspondence between
. This rapid component became a preferential object of research in the field ever since, particularly by the British school led by Brian Whipp. It was integrated in the subsequent double-exponential model of the exercise transient, proposed by Barstow and Molé (1987). It also restricted the domain of application of the concept of a correspondence between 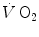 response at the mouth and in muscle to the second exponential only, whose time delay was taken to represent the physiological delay between muscle and mouth
response at the mouth and in muscle to the second exponential only, whose time delay was taken to represent the physiological delay between muscle and mouth 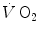 increase.
increase.
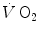 response during the square wave exercise transient. Wasserman et al. (1974) were the first to realize that there might be a rapid component in the earliest phase of the exercise transient, which they attributed to a sudden increase in cardiac output
response during the square wave exercise transient. Wasserman et al. (1974) were the first to realize that there might be a rapid component in the earliest phase of the exercise transient, which they attributed to a sudden increase in cardiac output 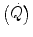 . This rapid component became a preferential object of research in the field ever since, particularly by the British school led by Brian Whipp. It was integrated in the subsequent double-exponential model of the exercise transient, proposed by Barstow and Molé (1987). It also restricted the domain of application of the concept of a correspondence between
. This rapid component became a preferential object of research in the field ever since, particularly by the British school led by Brian Whipp. It was integrated in the subsequent double-exponential model of the exercise transient, proposed by Barstow and Molé (1987). It also restricted the domain of application of the concept of a correspondence between 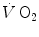 response at the mouth and in muscle to the second exponential only, whose time delay was taken to represent the physiological delay between muscle and mouth
response at the mouth and in muscle to the second exponential only, whose time delay was taken to represent the physiological delay between muscle and mouth 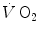 increase.
increase.In this chapter, I discuss first the energetics of the oxygen deficit, within the context of a mono-exponential model. These concepts still hold as long as, in a double-exponential context, accent is placed on the so-called primary component (or phase II) of the 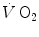 response. Then, I treat the implications of the double-exponential model and the cardiovascular transients, and I analyse the case of intense exercise, with the appearance of the so-called slow component, or phase III. Other exercise modalities than the square wave exercise will finally be considered.
response. Then, I treat the implications of the double-exponential model and the cardiovascular transients, and I analyse the case of intense exercise, with the appearance of the so-called slow component, or phase III. Other exercise modalities than the square wave exercise will finally be considered.
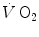 response. Then, I treat the implications of the double-exponential model and the cardiovascular transients, and I analyse the case of intense exercise, with the appearance of the so-called slow component, or phase III. Other exercise modalities than the square wave exercise will finally be considered.
response. Then, I treat the implications of the double-exponential model and the cardiovascular transients, and I analyse the case of intense exercise, with the appearance of the so-called slow component, or phase III. Other exercise modalities than the square wave exercise will finally be considered.The Energetics of the Oxygen Deficit During Light Exercise
The energy that 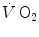 is unable to provide during the exercise transient comes essentially from three sources: (i) phosphocreatine breakdown, providing what is called the net alactic oxygen deficit; (ii) “early” lactate accumulation (Cerretelli et al. 1979); (iii) body oxygen stores. These components of the oxygen deficit are not necessarily called upon all together. As exercise starts, no lactate accumulation occurs except in the intense exercise domain. This was clearly demonstrated in the isolated–perfused dog muscle preparation by Piiper et al. (1968), who found a relatively rapid time constant for
is unable to provide during the exercise transient comes essentially from three sources: (i) phosphocreatine breakdown, providing what is called the net alactic oxygen deficit; (ii) “early” lactate accumulation (Cerretelli et al. 1979); (iii) body oxygen stores. These components of the oxygen deficit are not necessarily called upon all together. As exercise starts, no lactate accumulation occurs except in the intense exercise domain. This was clearly demonstrated in the isolated–perfused dog muscle preparation by Piiper et al. (1968), who found a relatively rapid time constant for 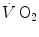 , faster than that usually observed in humans in the context of the single-exponential model of
, faster than that usually observed in humans in the context of the single-exponential model of 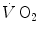 increase. Moreover, di Prampero and Margaria (1968) estimated a P/O2 ratio close to 6.17 from the ratio of phosphocreatine split to oxygen deficit (both expressed in moles per kg of wet muscle), clearly suggesting a primary role for phosphocreatine and anaerobic alactic metabolism in the genesis of the oxygen deficit.
increase. Moreover, di Prampero and Margaria (1968) estimated a P/O2 ratio close to 6.17 from the ratio of phosphocreatine split to oxygen deficit (both expressed in moles per kg of wet muscle), clearly suggesting a primary role for phosphocreatine and anaerobic alactic metabolism in the genesis of the oxygen deficit.
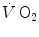 is unable to provide during the exercise transient comes essentially from three sources: (i) phosphocreatine breakdown, providing what is called the net alactic oxygen deficit; (ii) “early” lactate accumulation (Cerretelli et al. 1979); (iii) body oxygen stores. These components of the oxygen deficit are not necessarily called upon all together. As exercise starts, no lactate accumulation occurs except in the intense exercise domain. This was clearly demonstrated in the isolated–perfused dog muscle preparation by Piiper et al. (1968), who found a relatively rapid time constant for
is unable to provide during the exercise transient comes essentially from three sources: (i) phosphocreatine breakdown, providing what is called the net alactic oxygen deficit; (ii) “early” lactate accumulation (Cerretelli et al. 1979); (iii) body oxygen stores. These components of the oxygen deficit are not necessarily called upon all together. As exercise starts, no lactate accumulation occurs except in the intense exercise domain. This was clearly demonstrated in the isolated–perfused dog muscle preparation by Piiper et al. (1968), who found a relatively rapid time constant for 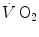 , faster than that usually observed in humans in the context of the single-exponential model of
, faster than that usually observed in humans in the context of the single-exponential model of 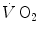 increase. Moreover, di Prampero and Margaria (1968) estimated a P/O2 ratio close to 6.17 from the ratio of phosphocreatine split to oxygen deficit (both expressed in moles per kg of wet muscle), clearly suggesting a primary role for phosphocreatine and anaerobic alactic metabolism in the genesis of the oxygen deficit.
increase. Moreover, di Prampero and Margaria (1968) estimated a P/O2 ratio close to 6.17 from the ratio of phosphocreatine split to oxygen deficit (both expressed in moles per kg of wet muscle), clearly suggesting a primary role for phosphocreatine and anaerobic alactic metabolism in the genesis of the oxygen deficit.In fact during light aerobic exercise in normoxia, when no early lactate accumulation takes place and body oxygen stores do not vary, the entire amount of energy released to build the oxygen deficit comes from the hydrolysis of high-energy phosphates, so that the energetics of the exercise transient can be summarized by the following equation:
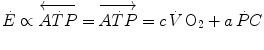
Equation (3.1) is nothing but a simplified version of the general equation of the energetics of muscular exercise (see Chap. 2, Eq. 2.1) for the specific case of a system in which only two metabolic energy sources are simultaneously active. In Eq. (3.1), 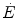 is the overall metabolic power,
is the overall metabolic power, 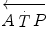 and
and 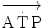 are the rates of ATP splitting and resynthesis, respectively, which during constant-power square wave exercise are equal, and the two constants a and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolyzed and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1. On the other hand, c is equal to the P/O2 ratio.
are the rates of ATP splitting and resynthesis, respectively, which during constant-power square wave exercise are equal, and the two constants a and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolyzed and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1. On the other hand, c is equal to the P/O2 ratio.
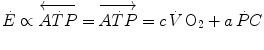
(3.1)
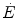 is the overall metabolic power,
is the overall metabolic power, 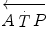 and
and 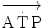 are the rates of ATP splitting and resynthesis, respectively, which during constant-power square wave exercise are equal, and the two constants a and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolyzed and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1. On the other hand, c is equal to the P/O2 ratio.
are the rates of ATP splitting and resynthesis, respectively, which during constant-power square wave exercise are equal, and the two constants a and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolyzed and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1. On the other hand, c is equal to the P/O2 ratio.In case of constant-power square wave exercise, as long as during the exercise transient 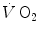 goes up,
goes up, 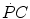 goes down in such a way as to maintain the sum
goes down in such a way as to maintain the sum 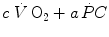 invariant. In the context of the mono-exponential model of
invariant. In the context of the mono-exponential model of 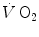 increase upon exercise onset, at the very start of exercise (exercise time 0), all the
increase upon exercise onset, at the very start of exercise (exercise time 0), all the 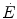 above the resting metabolic rate is therefore from anaerobic alactic metabolism, so that Eq. (3.1) becomes
above the resting metabolic rate is therefore from anaerobic alactic metabolism, so that Eq. (3.1) becomes
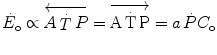
where suffix 0 indicates the exercise time 0. This being so, then we have
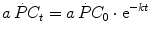
where t is time and k is the velocity constant (reciprocal of the time constant τ). In a system like the one represented by Eq. (3.1), if 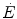 is invariant, then k must take the same value for the
is invariant, then k must take the same value for the 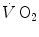 and the
and the 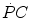 kinetics. Moreover, since at any t a positive value of
kinetics. Moreover, since at any t a positive value of 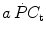 implies a given finite reduction of muscle phosphocreatine concentration ([PC]), then the time course of muscle [PC] changes during the exercise transient is also described by a mono-exponential equation, whose k takes the same value as the one obtained from Eq. (3.3). Finally, the time integral of Eq. (3.3) provides the overall amount of phosphocreatine that has been hydrolyzed during the exercise transient in order to cover the oxygen deficit. This amount is directly proportional to the oxygen deficit and thus to the applied mechanical power, so that there must be a negative linear relationship between [PC] and
implies a given finite reduction of muscle phosphocreatine concentration ([PC]), then the time course of muscle [PC] changes during the exercise transient is also described by a mono-exponential equation, whose k takes the same value as the one obtained from Eq. (3.3). Finally, the time integral of Eq. (3.3) provides the overall amount of phosphocreatine that has been hydrolyzed during the exercise transient in order to cover the oxygen deficit. This amount is directly proportional to the oxygen deficit and thus to the applied mechanical power, so that there must be a negative linear relationship between [PC] and 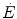 .
.
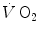 goes up,
goes up, 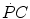 goes down in such a way as to maintain the sum
goes down in such a way as to maintain the sum 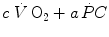 invariant. In the context of the mono-exponential model of
invariant. In the context of the mono-exponential model of 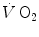 increase upon exercise onset, at the very start of exercise (exercise time 0), all the
increase upon exercise onset, at the very start of exercise (exercise time 0), all the 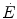 above the resting metabolic rate is therefore from anaerobic alactic metabolism, so that Eq. (3.1) becomes
above the resting metabolic rate is therefore from anaerobic alactic metabolism, so that Eq. (3.1) becomes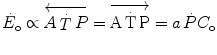
(3.2)
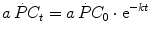
(3.3)
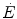 is invariant, then k must take the same value for the
is invariant, then k must take the same value for the 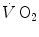 and the
and the 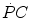 kinetics. Moreover, since at any t a positive value of
kinetics. Moreover, since at any t a positive value of 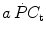 implies a given finite reduction of muscle phosphocreatine concentration ([PC]), then the time course of muscle [PC] changes during the exercise transient is also described by a mono-exponential equation, whose k takes the same value as the one obtained from Eq. (3.3). Finally, the time integral of Eq. (3.3) provides the overall amount of phosphocreatine that has been hydrolyzed during the exercise transient in order to cover the oxygen deficit. This amount is directly proportional to the oxygen deficit and thus to the applied mechanical power, so that there must be a negative linear relationship between [PC] and
implies a given finite reduction of muscle phosphocreatine concentration ([PC]), then the time course of muscle [PC] changes during the exercise transient is also described by a mono-exponential equation, whose k takes the same value as the one obtained from Eq. (3.3). Finally, the time integral of Eq. (3.3) provides the overall amount of phosphocreatine that has been hydrolyzed during the exercise transient in order to cover the oxygen deficit. This amount is directly proportional to the oxygen deficit and thus to the applied mechanical power, so that there must be a negative linear relationship between [PC] and 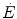 .
.These concepts have received wide experimental support. Values for τ comprised between 20 and 25 s were found for mono-exponential [PC] kinetics on the isolated–perfused dog muscle preparation (Piiper et al. 1968). The same authors demonstrated the negative linear relationship between [PC] and 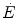 . Concerning humans, a remarkable breakthrough was generated by the technological evolution of magnetic resonance spectroscopy, which allowed obtaining serial relative non-invasive determinations of high-energy phosphates in human muscle during contractions. This allowed the assessment of the kinetics of phosphocreatine decrease upon square wave exercise onset, for which Binzoni et al. (1992) obtained a τ value of 23.4 s. The same authors demonstrated also in humans the negative linear relationship between [PC] and
. Concerning humans, a remarkable breakthrough was generated by the technological evolution of magnetic resonance spectroscopy, which allowed obtaining serial relative non-invasive determinations of high-energy phosphates in human muscle during contractions. This allowed the assessment of the kinetics of phosphocreatine decrease upon square wave exercise onset, for which Binzoni et al. (1992) obtained a τ value of 23.4 s. The same authors demonstrated also in humans the negative linear relationship between [PC] and 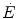 . Similar results were later obtained by other authors (di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002). This τ value for [PC] was also found to be independent of the exercise intensity (Binzoni et al. 1997), so that (i) the cumulative oxygen deficit of step-increasing powers up to a given level turns out equal to the oxygen deficit incurred if that very same level is attained in a unique step, and (ii) the oxygen deficit is directly proportional to the steady-state
. Similar results were later obtained by other authors (di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002). This τ value for [PC] was also found to be independent of the exercise intensity (Binzoni et al. 1997), so that (i) the cumulative oxygen deficit of step-increasing powers up to a given level turns out equal to the oxygen deficit incurred if that very same level is attained in a unique step, and (ii) the oxygen deficit is directly proportional to the steady-state 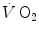 , with τ as proportionality constant.
, with τ as proportionality constant.
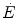 . Concerning humans, a remarkable breakthrough was generated by the technological evolution of magnetic resonance spectroscopy, which allowed obtaining serial relative non-invasive determinations of high-energy phosphates in human muscle during contractions. This allowed the assessment of the kinetics of phosphocreatine decrease upon square wave exercise onset, for which Binzoni et al. (1992) obtained a τ value of 23.4 s. The same authors demonstrated also in humans the negative linear relationship between [PC] and
. Concerning humans, a remarkable breakthrough was generated by the technological evolution of magnetic resonance spectroscopy, which allowed obtaining serial relative non-invasive determinations of high-energy phosphates in human muscle during contractions. This allowed the assessment of the kinetics of phosphocreatine decrease upon square wave exercise onset, for which Binzoni et al. (1992) obtained a τ value of 23.4 s. The same authors demonstrated also in humans the negative linear relationship between [PC] and 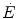 . Similar results were later obtained by other authors (di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002). This τ value for [PC] was also found to be independent of the exercise intensity (Binzoni et al. 1997), so that (i) the cumulative oxygen deficit of step-increasing powers up to a given level turns out equal to the oxygen deficit incurred if that very same level is attained in a unique step, and (ii) the oxygen deficit is directly proportional to the steady-state
. Similar results were later obtained by other authors (di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002). This τ value for [PC] was also found to be independent of the exercise intensity (Binzoni et al. 1997), so that (i) the cumulative oxygen deficit of step-increasing powers up to a given level turns out equal to the oxygen deficit incurred if that very same level is attained in a unique step, and (ii) the oxygen deficit is directly proportional to the steady-state 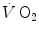 , with τ as proportionality constant.
, with τ as proportionality constant.Single-leg extension exercise was also used as a tool to gain insight into the muscle oxygen consumption kinetics in humans (Grassi et al. 1996; Koga et al. 2005). These studies provided τ values similar to those for [PC]. A direct comparison between the τ of 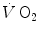 during single-leg exercise and the τ of [PC] on the same subjects during the same exercise transients further reinforced this notion (Rossiter et al. 1999) (Fig. 3.1). Finally, on the isolated–perfused dog muscle preparation, the τ of muscle oxygen consumption was found to be equal in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease (Grassi et al. 1998), demonstrating that there is at least some peripheral components of the kinetics of muscle oxygen consumption which are fully independent of muscle oxygen delivery.
during single-leg exercise and the τ of [PC] on the same subjects during the same exercise transients further reinforced this notion (Rossiter et al. 1999) (Fig. 3.1). Finally, on the isolated–perfused dog muscle preparation, the τ of muscle oxygen consumption was found to be equal in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease (Grassi et al. 1998), demonstrating that there is at least some peripheral components of the kinetics of muscle oxygen consumption which are fully independent of muscle oxygen delivery.
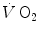 during single-leg exercise and the τ of [PC] on the same subjects during the same exercise transients further reinforced this notion (Rossiter et al. 1999) (Fig. 3.1). Finally, on the isolated–perfused dog muscle preparation, the τ of muscle oxygen consumption was found to be equal in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease (Grassi et al. 1998), demonstrating that there is at least some peripheral components of the kinetics of muscle oxygen consumption which are fully independent of muscle oxygen delivery.
during single-leg exercise and the τ of [PC] on the same subjects during the same exercise transients further reinforced this notion (Rossiter et al. 1999) (Fig. 3.1). Finally, on the isolated–perfused dog muscle preparation, the τ of muscle oxygen consumption was found to be equal in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease (Grassi et al. 1998), demonstrating that there is at least some peripheral components of the kinetics of muscle oxygen consumption which are fully independent of muscle oxygen delivery.
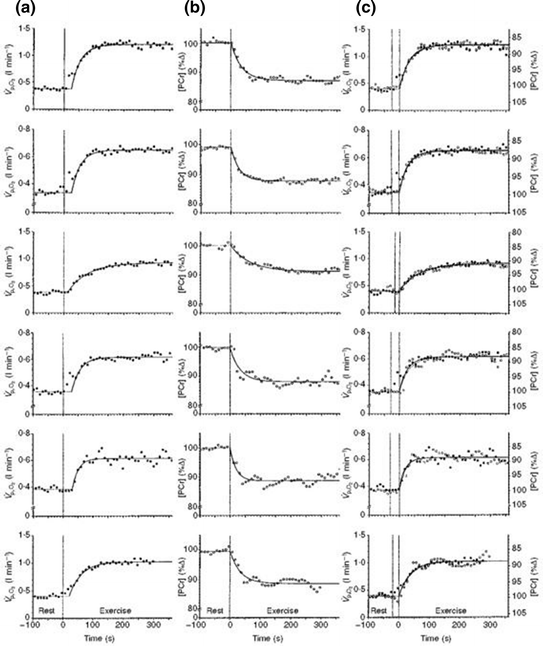
Fig. 3.1
Comparative kinetics of oxygen consumption 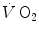 and phosphocreatine concentration [PC] during constant-load exercise in six subjects. a
and phosphocreatine concentration [PC] during constant-load exercise in six subjects. a 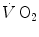 as a function of time, with the phase II response fitted by a mono-exponential. b [PC] as a function of time, simultaneously determined on the same subjects. c demonstration of the identity of phase II
as a function of time, with the phase II response fitted by a mono-exponential. b [PC] as a function of time, simultaneously determined on the same subjects. c demonstration of the identity of phase II 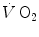 (black circle) and [PC] (white circle) kinetics determined simultaneously during quadriceps exercise. The [PCr] scale is inverted to facilitate comparisons. From Rossiter et al. (1999)
(black circle) and [PC] (white circle) kinetics determined simultaneously during quadriceps exercise. The [PCr] scale is inverted to facilitate comparisons. From Rossiter et al. (1999)
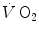 and phosphocreatine concentration [PC] during constant-load exercise in six subjects. a
and phosphocreatine concentration [PC] during constant-load exercise in six subjects. a 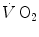 as a function of time, with the phase II response fitted by a mono-exponential. b [PC] as a function of time, simultaneously determined on the same subjects. c demonstration of the identity of phase II
as a function of time, with the phase II response fitted by a mono-exponential. b [PC] as a function of time, simultaneously determined on the same subjects. c demonstration of the identity of phase II 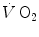 (black circle) and [PC] (white circle) kinetics determined simultaneously during quadriceps exercise. The [PCr] scale is inverted to facilitate comparisons. From Rossiter et al. (1999)
(black circle) and [PC] (white circle) kinetics determined simultaneously during quadriceps exercise. The [PCr] scale is inverted to facilitate comparisons. From Rossiter et al. (1999)More recently, however, faster mono-exponential τ values were obtained (Cautero et al. 2002; Lador et al. 2006) than in the classical studies (di Prampero 1981; Linnarsson 1974) with the same exercise mode and intensities, possibly as a consequence of improved signal-to-noise ratio in breath-by-breath 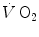 computation (Capelli et al. 2001). The τ values for
computation (Capelli et al. 2001). The τ values for 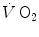 reported in those studies were also faster than those found for the mono-exponential phosphocreatine decrease upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Rossiter et al. 1999). These fast time constants suggest the possibility that the correspondence between lung
reported in those studies were also faster than those found for the mono-exponential phosphocreatine decrease upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Rossiter et al. 1999). These fast time constants suggest the possibility that the correspondence between lung 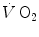 and muscle oxygen consumption may not be so good under certain circumstances. It was then demonstrated that lung
and muscle oxygen consumption may not be so good under certain circumstances. It was then demonstrated that lung 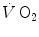 kinetics can be accelerated by prior exercise performance (Faisal et al. 2009), possibly as a consequence of maintained muscle vasodilation after completion of the first exercise bout (Faisal et al. 2010). Although, and especially when classical computational algorithms are employed, the lung
kinetics can be accelerated by prior exercise performance (Faisal et al. 2009), possibly as a consequence of maintained muscle vasodilation after completion of the first exercise bout (Faisal et al. 2010). Although, and especially when classical computational algorithms are employed, the lung 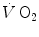 kinetics may indeed result equivalent to the muscle oxygen consumption kinetics, this correspondence may be fortuitous: different mechanisms may be implicated in the two transients. This does not mean, however, that the above energetic interpretation of the oxygen deficit is to be rejected. This means only that the energetic analysis of the oxygen deficit performed on the basis of lung
kinetics may indeed result equivalent to the muscle oxygen consumption kinetics, this correspondence may be fortuitous: different mechanisms may be implicated in the two transients. This does not mean, however, that the above energetic interpretation of the oxygen deficit is to be rejected. This means only that the energetic analysis of the oxygen deficit performed on the basis of lung 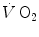 kinetics may provide an underestimate with respect to the oxygen deficit incurred in the contracting muscles. Nevertheless, I feel confident in stating that whenever the τ of lung
kinetics may provide an underestimate with respect to the oxygen deficit incurred in the contracting muscles. Nevertheless, I feel confident in stating that whenever the τ of lung 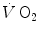 kinetics is lower (faster) than or at most equal to that of muscle oxygen consumption, we deal with a dual energetic system like the one represented by Eq. (3.1): no early lactate accumulation occurs under these circumstances, and the kinetics of muscle [PC] is a mirror image of that of muscle oxygen consumption.
kinetics is lower (faster) than or at most equal to that of muscle oxygen consumption, we deal with a dual energetic system like the one represented by Eq. (3.1): no early lactate accumulation occurs under these circumstances, and the kinetics of muscle [PC] is a mirror image of that of muscle oxygen consumption.
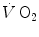 computation (Capelli et al. 2001). The τ values for
computation (Capelli et al. 2001). The τ values for 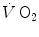 reported in those studies were also faster than those found for the mono-exponential phosphocreatine decrease upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Rossiter et al. 1999). These fast time constants suggest the possibility that the correspondence between lung
reported in those studies were also faster than those found for the mono-exponential phosphocreatine decrease upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Rossiter et al. 1999). These fast time constants suggest the possibility that the correspondence between lung 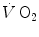 and muscle oxygen consumption may not be so good under certain circumstances. It was then demonstrated that lung
and muscle oxygen consumption may not be so good under certain circumstances. It was then demonstrated that lung 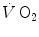 kinetics can be accelerated by prior exercise performance (Faisal et al. 2009), possibly as a consequence of maintained muscle vasodilation after completion of the first exercise bout (Faisal et al. 2010). Although, and especially when classical computational algorithms are employed, the lung
kinetics can be accelerated by prior exercise performance (Faisal et al. 2009), possibly as a consequence of maintained muscle vasodilation after completion of the first exercise bout (Faisal et al. 2010). Although, and especially when classical computational algorithms are employed, the lung 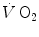 kinetics may indeed result equivalent to the muscle oxygen consumption kinetics, this correspondence may be fortuitous: different mechanisms may be implicated in the two transients. This does not mean, however, that the above energetic interpretation of the oxygen deficit is to be rejected. This means only that the energetic analysis of the oxygen deficit performed on the basis of lung
kinetics may indeed result equivalent to the muscle oxygen consumption kinetics, this correspondence may be fortuitous: different mechanisms may be implicated in the two transients. This does not mean, however, that the above energetic interpretation of the oxygen deficit is to be rejected. This means only that the energetic analysis of the oxygen deficit performed on the basis of lung 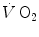 kinetics may provide an underestimate with respect to the oxygen deficit incurred in the contracting muscles. Nevertheless, I feel confident in stating that whenever the τ of lung
kinetics may provide an underestimate with respect to the oxygen deficit incurred in the contracting muscles. Nevertheless, I feel confident in stating that whenever the τ of lung 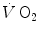 kinetics is lower (faster) than or at most equal to that of muscle oxygen consumption, we deal with a dual energetic system like the one represented by Eq. (3.1): no early lactate accumulation occurs under these circumstances, and the kinetics of muscle [PC] is a mirror image of that of muscle oxygen consumption.
kinetics is lower (faster) than or at most equal to that of muscle oxygen consumption, we deal with a dual energetic system like the one represented by Eq. (3.1): no early lactate accumulation occurs under these circumstances, and the kinetics of muscle [PC] is a mirror image of that of muscle oxygen consumption.Also, the introduction of bi-exponential models of the pulmonary 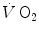 response at the exercise onset has contributed to a redefinition of the concept of a correspondence between lung
response at the exercise onset has contributed to a redefinition of the concept of a correspondence between lung 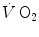 and muscle oxygen consumption kinetics. In this context, the first exponential (rapid phase or phase I) is fully unrelated to the events occurring in contracting muscles (see below). The domain of application of the same reasoning as above on the oxygen deficit is restricted to the second exponential (primary phase of phase II) (Whipp and Ward 1990).
and muscle oxygen consumption kinetics. In this context, the first exponential (rapid phase or phase I) is fully unrelated to the events occurring in contracting muscles (see below). The domain of application of the same reasoning as above on the oxygen deficit is restricted to the second exponential (primary phase of phase II) (Whipp and Ward 1990).
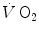 response at the exercise onset has contributed to a redefinition of the concept of a correspondence between lung
response at the exercise onset has contributed to a redefinition of the concept of a correspondence between lung 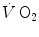 and muscle oxygen consumption kinetics. In this context, the first exponential (rapid phase or phase I) is fully unrelated to the events occurring in contracting muscles (see below). The domain of application of the same reasoning as above on the oxygen deficit is restricted to the second exponential (primary phase of phase II) (Whipp and Ward 1990).
and muscle oxygen consumption kinetics. In this context, the first exponential (rapid phase or phase I) is fully unrelated to the events occurring in contracting muscles (see below). The domain of application of the same reasoning as above on the oxygen deficit is restricted to the second exponential (primary phase of phase II) (Whipp and Ward 1990).The Energetics of the Oxygen Deficit During Intense Exercise
As far as early lactate is concerned, Cerretelli et al. (1979) reported that the τ of a mono-exponential 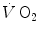 increase upon exercise onset is higher, the higher is the mechanical power applied, and thus, the higher is
increase upon exercise onset is higher, the higher is the mechanical power applied, and thus, the higher is 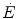 : they demonstrated in fact that τ is linearly related to the lactate accumulation in blood during the exercise transient, as described by the following:
: they demonstrated in fact that τ is linearly related to the lactate accumulation in blood during the exercise transient, as described by the following:
![$$ \tau =\uplambda\left[ {\text{La}} \right]_{\text{e}} + \tau_{0} $$](/wp-content/uploads/2016/09/A322139_1_En_3_Chapter_Equ4.gif)
where [La]e is early lactate (net blood lactate accumulation during the exercise transient), λ is a constant indicating how much τ increases per unit increase of lactate in blood during the exercise transient (di Prampero and Ferretti 1999), and τ 0 is the time constant that would incur in the absence of early lactate accumulation. The constant λ is an inverse function of the steady-state 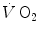 . From the data of Cerretelli et al. (1979), it results equal to 7.8 and 12.1 s mM−1 at a steady-state
. From the data of Cerretelli et al. (1979), it results equal to 7.8 and 12.1 s mM−1 at a steady-state 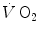 of 1.5 and 1.0 L min−1 (mechanical powers of 125 and 75 W), respectively (Fig. 3.2). These values allow computation of the oxygen deficit increase (in ml O2 kg−1) per unit increase in [La]e (in mM), which is nothing but the energy equivalent of blood lactate accumulation (see Chap. 6). This turns out equal to 2.19 and 2.89 ml kg−1 mM−1 for the 125 and 75 W powers, respectively, the latter value agreeing well with those reported in Chap. 6 (di Prampero 1981). On the other hand, the constant τ 0 corresponds to the time constant that one would observe in the two-component system described by Eq. (3.1) and thus to the time constant of muscle phosphocreatine decrease (see above). Considering the error due to extrapolation of a regression equation and neglecting possible though small changes in blood oxygen stores, the obtained value of τ 0 as from Fig. 3.2 (24.5 and 29.7 s for the two reported equations) corresponds very well to those reported from P-NMR studies for phosphocreatine decrease (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002).
of 1.5 and 1.0 L min−1 (mechanical powers of 125 and 75 W), respectively (Fig. 3.2). These values allow computation of the oxygen deficit increase (in ml O2 kg−1) per unit increase in [La]e (in mM), which is nothing but the energy equivalent of blood lactate accumulation (see Chap. 6). This turns out equal to 2.19 and 2.89 ml kg−1 mM−1 for the 125 and 75 W powers, respectively, the latter value agreeing well with those reported in Chap. 6 (di Prampero 1981). On the other hand, the constant τ 0 corresponds to the time constant that one would observe in the two-component system described by Eq. (3.1) and thus to the time constant of muscle phosphocreatine decrease (see above). Considering the error due to extrapolation of a regression equation and neglecting possible though small changes in blood oxygen stores, the obtained value of τ 0 as from Fig. 3.2 (24.5 and 29.7 s for the two reported equations) corresponds very well to those reported from P-NMR studies for phosphocreatine decrease (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002).
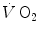 increase upon exercise onset is higher, the higher is the mechanical power applied, and thus, the higher is
increase upon exercise onset is higher, the higher is the mechanical power applied, and thus, the higher is 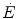 : they demonstrated in fact that τ is linearly related to the lactate accumulation in blood during the exercise transient, as described by the following:
: they demonstrated in fact that τ is linearly related to the lactate accumulation in blood during the exercise transient, as described by the following:![$$ \tau =\uplambda\left[ {\text{La}} \right]_{\text{e}} + \tau_{0} $$](/wp-content/uploads/2016/09/A322139_1_En_3_Chapter_Equ4.gif)
(3.4)
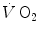 . From the data of Cerretelli et al. (1979), it results equal to 7.8 and 12.1 s mM−1 at a steady-state
. From the data of Cerretelli et al. (1979), it results equal to 7.8 and 12.1 s mM−1 at a steady-state 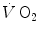 of 1.5 and 1.0 L min−1 (mechanical powers of 125 and 75 W), respectively (Fig. 3.2). These values allow computation of the oxygen deficit increase (in ml O2 kg−1) per unit increase in [La]e (in mM), which is nothing but the energy equivalent of blood lactate accumulation (see Chap. 6). This turns out equal to 2.19 and 2.89 ml kg−1 mM−1 for the 125 and 75 W powers, respectively, the latter value agreeing well with those reported in Chap. 6 (di Prampero 1981). On the other hand, the constant τ 0 corresponds to the time constant that one would observe in the two-component system described by Eq. (3.1) and thus to the time constant of muscle phosphocreatine decrease (see above). Considering the error due to extrapolation of a regression equation and neglecting possible though small changes in blood oxygen stores, the obtained value of τ 0 as from Fig. 3.2 (24.5 and 29.7 s for the two reported equations) corresponds very well to those reported from P-NMR studies for phosphocreatine decrease (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002).
of 1.5 and 1.0 L min−1 (mechanical powers of 125 and 75 W), respectively (Fig. 3.2). These values allow computation of the oxygen deficit increase (in ml O2 kg−1) per unit increase in [La]e (in mM), which is nothing but the energy equivalent of blood lactate accumulation (see Chap. 6). This turns out equal to 2.19 and 2.89 ml kg−1 mM−1 for the 125 and 75 W powers, respectively, the latter value agreeing well with those reported in Chap. 6 (di Prampero 1981). On the other hand, the constant τ 0 corresponds to the time constant that one would observe in the two-component system described by Eq. (3.1) and thus to the time constant of muscle phosphocreatine decrease (see above). Considering the error due to extrapolation of a regression equation and neglecting possible though small changes in blood oxygen stores, the obtained value of τ 0 as from Fig. 3.2 (24.5 and 29.7 s for the two reported equations) corresponds very well to those reported from P-NMR studies for phosphocreatine decrease (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2013; Rossiter et al. 1999, 2002).
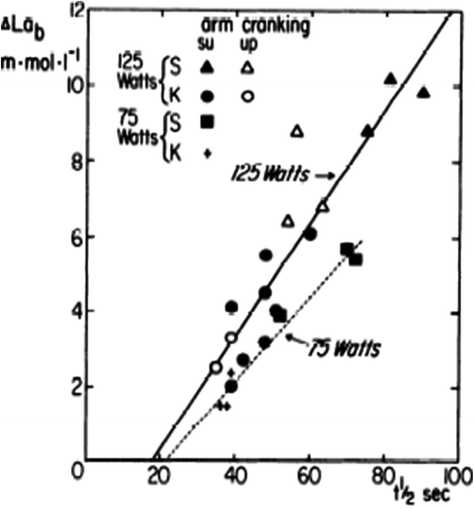
Fig. 3.2
Net blood lactate accumulation (Δ[La]b) at min 6 of square wave exercises of the type and intensity indicated on the graph as a function of the half-time (t ½) of the exponential oxygen uptake increase upon exercise onset. From Cerretelli et al. (1979). Note that t ½ = 0.75 τ. Note also that the representation proposed by Cerretelli et al. (1979) corresponds to the solution of Eq. (3.4) for [La]b, which they considered as the independent variable. In this representation, the constant τ 0 of Eq. (3.4) is given by the x-axis intercept of the reported relationships (in fact t ½,0 in the graph)
Thus, above a given power, which I postulate to correspond to the critical power (Chap. 5), the overall oxygen deficit becomes larger than the net alactic oxygen deficit, so that τ becomes higher than that of muscle [PC] drop: the energy gap is bridged by the appearance of early lactate accumulation. This being so, the difference between the overall oxygen deficit and the net alactic oxygen deficit can be precisely predicted from the amount of [La]e and the energy equivalent of blood lactate accumulation. It is of note that at such intense powers, the lung 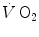 kinetics may indeed correspond to the muscle oxygen consumption kinetics, so that the overall oxygen deficit determined at the lungs would reflect the overall oxygen deficit incurred in the contracting muscles. But this does not inform on the alactic oxygen deficit. It is only the x-axis intercept of Fig. 3.2 (τ 0) that corresponds to the τ of the kinetics of muscle [PC] drop, if we assume that the effects of changes in oxygen stores are nil.
kinetics may indeed correspond to the muscle oxygen consumption kinetics, so that the overall oxygen deficit determined at the lungs would reflect the overall oxygen deficit incurred in the contracting muscles. But this does not inform on the alactic oxygen deficit. It is only the x-axis intercept of Fig. 3.2 (τ 0) that corresponds to the τ of the kinetics of muscle [PC] drop, if we assume that the effects of changes in oxygen stores are nil.
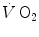 kinetics may indeed correspond to the muscle oxygen consumption kinetics, so that the overall oxygen deficit determined at the lungs would reflect the overall oxygen deficit incurred in the contracting muscles. But this does not inform on the alactic oxygen deficit. It is only the x-axis intercept of Fig. 3.2 (τ 0) that corresponds to the τ of the kinetics of muscle [PC] drop, if we assume that the effects of changes in oxygen stores are nil.
kinetics may indeed correspond to the muscle oxygen consumption kinetics, so that the overall oxygen deficit determined at the lungs would reflect the overall oxygen deficit incurred in the contracting muscles. But this does not inform on the alactic oxygen deficit. It is only the x-axis intercept of Fig. 3.2 (τ 0) that corresponds to the τ of the kinetics of muscle [PC] drop, if we assume that the effects of changes in oxygen stores are nil.As a consequence of the diffusion–perfusion interaction equation for peripheral gas exchange (see Chap. 2) and of the reduction of capillary contact time, the amount of oxygen stored in the body during steady-state exercise is smaller, the higher is the exercise intensity, essentially because of lower oxygen concentration in mixed venous blood. Thus, the amount of energy constituting the oxygen deficit that is derived from oxygen stores becomes predictably smaller in a given transition from light to heavier work load than in an equivalent transition from rest to exercise. In fact, the τ of a mono-exponential lung 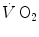 kinetics was found to be lower (faster) in the former than in the latter case (di Prampero et al. 1970). Similarly, in acute normobaric hypoxia, a condition obviously characterized by decreased oxygen stores, the oxygen deficit was coherently smaller for equivalent early lactate accumulation (di Prampero et al. 1983). In other terms, oxygen stores may be viewed as a kind of buffer between contracting muscles and lungs, the size of which may slightly vary the lung
kinetics was found to be lower (faster) in the former than in the latter case (di Prampero et al. 1970). Similarly, in acute normobaric hypoxia, a condition obviously characterized by decreased oxygen stores, the oxygen deficit was coherently smaller for equivalent early lactate accumulation (di Prampero et al. 1983). In other terms, oxygen stores may be viewed as a kind of buffer between contracting muscles and lungs, the size of which may slightly vary the lung 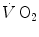 kinetics. Of course, this does not mean that overall the lung
kinetics. Of course, this does not mean that overall the lung 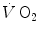 kinetics is faster in hypoxia than in normoxia. In fact, it was shown to be slower in the former condition than in the latter (Engelen et al. 1996; Hughson and Kowalchuk 1995; Xing et al. 1991), as a consequence of increased early lactate accumulation at equivalent work load (Lador et al. 2013).
kinetics is faster in hypoxia than in normoxia. In fact, it was shown to be slower in the former condition than in the latter (Engelen et al. 1996; Hughson and Kowalchuk 1995; Xing et al. 1991), as a consequence of increased early lactate accumulation at equivalent work load (Lador et al. 2013).
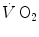 kinetics was found to be lower (faster) in the former than in the latter case (di Prampero et al. 1970). Similarly, in acute normobaric hypoxia, a condition obviously characterized by decreased oxygen stores, the oxygen deficit was coherently smaller for equivalent early lactate accumulation (di Prampero et al. 1983). In other terms, oxygen stores may be viewed as a kind of buffer between contracting muscles and lungs, the size of which may slightly vary the lung
kinetics was found to be lower (faster) in the former than in the latter case (di Prampero et al. 1970). Similarly, in acute normobaric hypoxia, a condition obviously characterized by decreased oxygen stores, the oxygen deficit was coherently smaller for equivalent early lactate accumulation (di Prampero et al. 1983). In other terms, oxygen stores may be viewed as a kind of buffer between contracting muscles and lungs, the size of which may slightly vary the lung 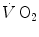 kinetics. Of course, this does not mean that overall the lung
kinetics. Of course, this does not mean that overall the lung 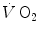 kinetics is faster in hypoxia than in normoxia. In fact, it was shown to be slower in the former condition than in the latter (Engelen et al. 1996; Hughson and Kowalchuk 1995; Xing et al. 1991), as a consequence of increased early lactate accumulation at equivalent work load (Lador et al. 2013).
kinetics is faster in hypoxia than in normoxia. In fact, it was shown to be slower in the former condition than in the latter (Engelen et al. 1996; Hughson and Kowalchuk 1995; Xing et al. 1991), as a consequence of increased early lactate accumulation at equivalent work load (Lador et al. 2013).Mechanisms Underlying the Oxygen Deficit
The contraction of the net alactic oxygen deficit is a physiological necessity. It is unavoidable at exercise onset because the key enzymes of glycolysis need to be activated in order to sustain an increase in the rate of glycolytic energy fluxes. Phospho-fructo-kinase (PFK) is the key enzyme of glycolysis whose activity is modulated by the concentration of high-energy phosphates: a decrease in [PC] accelerates its kinetics as does an increase in inorganic phosphate concentration ([Pi]). The drop of [PC] carries along also an augmentation of adenosine di-phosphate ([ADP]) and of [Pi], so that the so-called phosphorylation potential {[ATP]/([ADP] + [Pi])} is increased. This is a key controller of oxidative phosphorylation in the mitochondria (Korzeniewski 2003; Meyer and Foley 1996). Thus, the priming of aerobic metabolism requires an initial drop of [PC].
As exercise starts, immediately available ATP in the cytosol of the muscle fibres is used in the cross-bridge cycle and is immediately resynthesized by the Lohmann’s reaction. The subsequent drop of muscle [PC] accelerates PFK activity, and thus the energy flux along the glycolytic pathway, and prompts the aerobic metabolism overall through a reduction of the phosphorylation potential. This chain of events supports the concept that the relatively slow increase of muscle oxygen consumption at exercise onset has a metabolic origin (di Prampero 1981; di Prampero and Ferretti 1999; Grassi 2000), as opposed to the alternative concept that the oxygen deficit is imposed by the delayed response of the respiratory system (Hughson et al. 2001; Whipp and Ward 1982). In this context, the τ of the muscle [PC] fall upon exercise onset describes the τ of glycolysis activation.
However, the acceleration of glycolysis and of all subsequent metabolic pathways that are summarized in the concept of aerobic metabolism requires an adequate amount of oxygen to be made available in the mitochondria of the active muscle mass. This amount of oxygen is taken up from ambient air and transferred to the mitochondria along the respiratory system. A tight match between the rate of glycolysis acceleration and the rate of oxygen flow in the respiratory system upon exercise onset is needed in order to have equal τ values for the [PC] fall and the 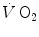 increase in the exercise transient. Only the respect of this condition warrants that we deal indeed with a dual energetic system (aerobic metabolism plus anaerobic alactic metabolism) in the exercise transient. More likely, however, during light aerobic exercise, the
increase in the exercise transient. Only the respect of this condition warrants that we deal indeed with a dual energetic system (aerobic metabolism plus anaerobic alactic metabolism) in the exercise transient. More likely, however, during light aerobic exercise, the 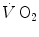 kinetics is faster than that of muscle oxygen consumption: although in this case the oxygen deficit incurred in the lungs is lower than, and so does not reflect the muscle oxygen deficit, nevertheless, we still deal with a dual energetic system, where differences in oxygen deficit between lungs and muscles are buffered by oxygen stores. The oxygen flow that the respiratory system is able to provide to the contracting muscle mass is sufficient to sustain the acceleration of glycolysis generated by the fall of [PC] at exercise start: in this case pyruvate, end product of glycolysis, can be entirely removed through the Krebs cycle and the new equilibrium is attained thanks to prompting of ATP resynthesis by aerobic metabolism only. Under these circumstances, the net alactic oxygen deficit represents indeed the entire oxygen deficit, a condition represented in Fig. 3.2 by the x-axis intercept of the regression line. This intercept defines the condition of evenly aerobic metabolism, in which all muscle fibres have sufficient oxygen delivery and oxidative capacity to sustain their aerobic metabolism.
kinetics is faster than that of muscle oxygen consumption: although in this case the oxygen deficit incurred in the lungs is lower than, and so does not reflect the muscle oxygen deficit, nevertheless, we still deal with a dual energetic system, where differences in oxygen deficit between lungs and muscles are buffered by oxygen stores. The oxygen flow that the respiratory system is able to provide to the contracting muscle mass is sufficient to sustain the acceleration of glycolysis generated by the fall of [PC] at exercise start: in this case pyruvate, end product of glycolysis, can be entirely removed through the Krebs cycle and the new equilibrium is attained thanks to prompting of ATP resynthesis by aerobic metabolism only. Under these circumstances, the net alactic oxygen deficit represents indeed the entire oxygen deficit, a condition represented in Fig. 3.2 by the x-axis intercept of the regression line. This intercept defines the condition of evenly aerobic metabolism, in which all muscle fibres have sufficient oxygen delivery and oxidative capacity to sustain their aerobic metabolism.
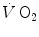 increase in the exercise transient. Only the respect of this condition warrants that we deal indeed with a dual energetic system (aerobic metabolism plus anaerobic alactic metabolism) in the exercise transient. More likely, however, during light aerobic exercise, the
increase in the exercise transient. Only the respect of this condition warrants that we deal indeed with a dual energetic system (aerobic metabolism plus anaerobic alactic metabolism) in the exercise transient. More likely, however, during light aerobic exercise, the 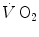 kinetics is faster than that of muscle oxygen consumption: although in this case the oxygen deficit incurred in the lungs is lower than, and so does not reflect the muscle oxygen deficit, nevertheless, we still deal with a dual energetic system, where differences in oxygen deficit between lungs and muscles are buffered by oxygen stores. The oxygen flow that the respiratory system is able to provide to the contracting muscle mass is sufficient to sustain the acceleration of glycolysis generated by the fall of [PC] at exercise start: in this case pyruvate, end product of glycolysis, can be entirely removed through the Krebs cycle and the new equilibrium is attained thanks to prompting of ATP resynthesis by aerobic metabolism only. Under these circumstances, the net alactic oxygen deficit represents indeed the entire oxygen deficit, a condition represented in Fig. 3.2 by the x-axis intercept of the regression line. This intercept defines the condition of evenly aerobic metabolism, in which all muscle fibres have sufficient oxygen delivery and oxidative capacity to sustain their aerobic metabolism.
kinetics is faster than that of muscle oxygen consumption: although in this case the oxygen deficit incurred in the lungs is lower than, and so does not reflect the muscle oxygen deficit, nevertheless, we still deal with a dual energetic system, where differences in oxygen deficit between lungs and muscles are buffered by oxygen stores. The oxygen flow that the respiratory system is able to provide to the contracting muscle mass is sufficient to sustain the acceleration of glycolysis generated by the fall of [PC] at exercise start: in this case pyruvate, end product of glycolysis, can be entirely removed through the Krebs cycle and the new equilibrium is attained thanks to prompting of ATP resynthesis by aerobic metabolism only. Under these circumstances, the net alactic oxygen deficit represents indeed the entire oxygen deficit, a condition represented in Fig. 3.2 by the x-axis intercept of the regression line. This intercept defines the condition of evenly aerobic metabolism, in which all muscle fibres have sufficient oxygen delivery and oxidative capacity to sustain their aerobic metabolism.By contrast, this is not so during intense exercise: in this case, the 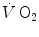 kinetics becomes slower than during light exercise (τ higher than τ 0), so that the
kinetics becomes slower than during light exercise (τ higher than τ 0), so that the 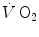 response does not follow the rate at which glycolysis is activated by the reduction of phosphorylation potential and does not provide the necessary amount of oxygen in due time. The postulate, supported by the NMR experiments of Binzoni et al. (1997), is that the rate of glycolysis activation at exercise onset is independent of the developed mechanical power, whereas the
response does not follow the rate at which glycolysis is activated by the reduction of phosphorylation potential and does not provide the necessary amount of oxygen in due time. The postulate, supported by the NMR experiments of Binzoni et al. (1997), is that the rate of glycolysis activation at exercise onset is independent of the developed mechanical power, whereas the 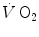 kinetics depends on the exercise intensity. When the time constant of the latter becomes higher than that of the former, the amount of oxygen made available by the respiratory system during the exercise transient is insufficient to ensure complete pyruvate removal through aerobic metabolism: oxidative phosphorylation and the Krebs cycle are unable to follow glycolysis acceleration anymore, so that a bottleneck appears, tending to increase muscle pyruvate concentration. As a consequence, the equilibrium of the reaction of pyruvate reduction to lactate is displaced towards lactate production, and lactate accumulates in muscle, then in blood, whence the appearance of early lactate.
kinetics depends on the exercise intensity. When the time constant of the latter becomes higher than that of the former, the amount of oxygen made available by the respiratory system during the exercise transient is insufficient to ensure complete pyruvate removal through aerobic metabolism: oxidative phosphorylation and the Krebs cycle are unable to follow glycolysis acceleration anymore, so that a bottleneck appears, tending to increase muscle pyruvate concentration. As a consequence, the equilibrium of the reaction of pyruvate reduction to lactate is displaced towards lactate production, and lactate accumulates in muscle, then in blood, whence the appearance of early lactate.
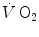 kinetics becomes slower than during light exercise (τ higher than τ 0), so that the
kinetics becomes slower than during light exercise (τ higher than τ 0), so that the 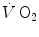 response does not follow the rate at which glycolysis is activated by the reduction of phosphorylation potential and does not provide the necessary amount of oxygen in due time. The postulate, supported by the NMR experiments of Binzoni et al. (1997), is that the rate of glycolysis activation at exercise onset is independent of the developed mechanical power, whereas the
response does not follow the rate at which glycolysis is activated by the reduction of phosphorylation potential and does not provide the necessary amount of oxygen in due time. The postulate, supported by the NMR experiments of Binzoni et al. (1997), is that the rate of glycolysis activation at exercise onset is independent of the developed mechanical power, whereas the 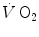 kinetics depends on the exercise intensity. When the time constant of the latter becomes higher than that of the former, the amount of oxygen made available by the respiratory system during the exercise transient is insufficient to ensure complete pyruvate removal through aerobic metabolism: oxidative phosphorylation and the Krebs cycle are unable to follow glycolysis acceleration anymore, so that a bottleneck appears, tending to increase muscle pyruvate concentration. As a consequence, the equilibrium of the reaction of pyruvate reduction to lactate is displaced towards lactate production, and lactate accumulates in muscle, then in blood, whence the appearance of early lactate.
kinetics depends on the exercise intensity. When the time constant of the latter becomes higher than that of the former, the amount of oxygen made available by the respiratory system during the exercise transient is insufficient to ensure complete pyruvate removal through aerobic metabolism: oxidative phosphorylation and the Krebs cycle are unable to follow glycolysis acceleration anymore, so that a bottleneck appears, tending to increase muscle pyruvate concentration. As a consequence, the equilibrium of the reaction of pyruvate reduction to lactate is displaced towards lactate production, and lactate accumulates in muscle, then in blood, whence the appearance of early lactate.The amount of lactate that is accumulated during a high-intensity exercise transient is proportional to the difference between the progressively increasing τ of the 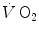 increase and the invariant τ of the [PC] fall (x-axis intercept of Fig. 3.2). The fraction of oxygen deficit that is due to early lactate accumulation—facultative component of the oxygen deficit—corresponds to the difference between the overall oxygen deficit and the fraction of oxygen deficit that is covered by [PC] hydrolysis. This last is the obligatory component of the oxygen deficit that is incurred anytime a human starts an exercise. For an invariant τ of the [PC] fall, as already pointed out, its amount depends only on the exercise intensity, i.e. on the mechanical power developed by muscle contraction. Conversely, the amount of energy provided by the facultative component of the oxygen deficit is directly proportional to the amount of early lactate that is accumulated, the proportionality constant being equal to the energy equivalent of blood lactate accumulation (see Chap. 6) (Lador et al. 2013 details given in Sect. 3.7).
increase and the invariant τ of the [PC] fall (x-axis intercept of Fig. 3.2). The fraction of oxygen deficit that is due to early lactate accumulation—facultative component of the oxygen deficit—corresponds to the difference between the overall oxygen deficit and the fraction of oxygen deficit that is covered by [PC] hydrolysis. This last is the obligatory component of the oxygen deficit that is incurred anytime a human starts an exercise. For an invariant τ of the [PC] fall, as already pointed out, its amount depends only on the exercise intensity, i.e. on the mechanical power developed by muscle contraction. Conversely, the amount of energy provided by the facultative component of the oxygen deficit is directly proportional to the amount of early lactate that is accumulated, the proportionality constant being equal to the energy equivalent of blood lactate accumulation (see Chap. 6) (Lador et al. 2013 details given in Sect. 3.7).
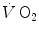 increase and the invariant τ of the [PC] fall (x-axis intercept of Fig. 3.2). The fraction of oxygen deficit that is due to early lactate accumulation—facultative component of the oxygen deficit—corresponds to the difference between the overall oxygen deficit and the fraction of oxygen deficit that is covered by [PC] hydrolysis. This last is the obligatory component of the oxygen deficit that is incurred anytime a human starts an exercise. For an invariant τ of the [PC] fall, as already pointed out, its amount depends only on the exercise intensity, i.e. on the mechanical power developed by muscle contraction. Conversely, the amount of energy provided by the facultative component of the oxygen deficit is directly proportional to the amount of early lactate that is accumulated, the proportionality constant being equal to the energy equivalent of blood lactate accumulation (see Chap. 6) (Lador et al. 2013 details given in Sect. 3.7).
increase and the invariant τ of the [PC] fall (x-axis intercept of Fig. 3.2). The fraction of oxygen deficit that is due to early lactate accumulation—facultative component of the oxygen deficit—corresponds to the difference between the overall oxygen deficit and the fraction of oxygen deficit that is covered by [PC] hydrolysis. This last is the obligatory component of the oxygen deficit that is incurred anytime a human starts an exercise. For an invariant τ of the [PC] fall, as already pointed out, its amount depends only on the exercise intensity, i.e. on the mechanical power developed by muscle contraction. Conversely, the amount of energy provided by the facultative component of the oxygen deficit is directly proportional to the amount of early lactate that is accumulated, the proportionality constant being equal to the energy equivalent of blood lactate accumulation (see Chap. 6) (Lador et al. 2013 details given in Sect. 3.7).A necessary consequence of the above reasoning is that the progressive increase of the τ of the 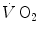 kinetics at intense exercise should be related to a progressively slower kinetics of cardiopulmonary variables. These were poorly investigated until beat-by-beat methods became available. Their quantitative analysis was carried out essentially in the context of a double-exponential model. Thus, I will introduce this model before discussing the dynamics of the cardiovascular responses to exercise.
kinetics at intense exercise should be related to a progressively slower kinetics of cardiopulmonary variables. These were poorly investigated until beat-by-beat methods became available. Their quantitative analysis was carried out essentially in the context of a double-exponential model. Thus, I will introduce this model before discussing the dynamics of the cardiovascular responses to exercise.
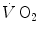 kinetics at intense exercise should be related to a progressively slower kinetics of cardiopulmonary variables. These were poorly investigated until beat-by-beat methods became available. Their quantitative analysis was carried out essentially in the context of a double-exponential model. Thus, I will introduce this model before discussing the dynamics of the cardiovascular responses to exercise.
kinetics at intense exercise should be related to a progressively slower kinetics of cardiopulmonary variables. These were poorly investigated until beat-by-beat methods became available. Their quantitative analysis was carried out essentially in the context of a double-exponential model. Thus, I will introduce this model before discussing the dynamics of the cardiovascular responses to exercise.The Double-exponential Model of 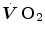 Kinetics
Kinetics
The double-exponential model, or two-phase model, of the 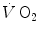 kinetics was proposed by Barstow and Molé (1987) after an original idea of Wasserman et al. (1974) refined by Whipp et al. (1982). This model foresees that an exponential increase in
kinetics was proposed by Barstow and Molé (1987) after an original idea of Wasserman et al. (1974) refined by Whipp et al. (1982). This model foresees that an exponential increase in 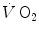 (phase II), related to metabolic adaptation in skeletal muscle, is preceded by a faster
(phase II), related to metabolic adaptation in skeletal muscle, is preceded by a faster 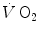 increase in the first seconds of exercise (phase I), which Barstow and Molé (1987) also treated as an exponential and which the British school led by Brian Whipp attributed to a rapid, also immediate cardiovascular response upon exercise onset (see, e.g. Whipp and Ward 1982, 1990). In the context of this model, the
increase in the first seconds of exercise (phase I), which Barstow and Molé (1987) also treated as an exponential and which the British school led by Brian Whipp attributed to a rapid, also immediate cardiovascular response upon exercise onset (see, e.g. Whipp and Ward 1982, 1990). In the context of this model, the 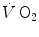 kinetics (measured value minus resting value) upon exercise onset is described by the following:
kinetics (measured value minus resting value) upon exercise onset is described by the following:
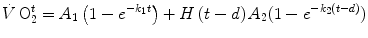
where 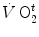 is the net
is the net 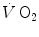 (measured value minus resting value) at time t, k 1 and k 2 are the velocity constants of the exponential
(measured value minus resting value) at time t, k 1 and k 2 are the velocity constants of the exponential 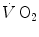 increase in phase I and II, respectively (their reciprocals τ 1 and τ 2 being the corresponding time constants), d is the time delay, and A 1 and A 2 are the amplitudes of the
increase in phase I and II, respectively (their reciprocals τ 1 and τ 2 being the corresponding time constants), d is the time delay, and A 1 and A 2 are the amplitudes of the 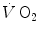 increase during phase I and phase II, respectively. H(t − d) is the associated Heaviside function, whose value is either 0 if t < d or 1 if t ≥ d.
increase during phase I and phase II, respectively. H(t − d) is the associated Heaviside function, whose value is either 0 if t < d or 1 if t ≥ d.
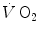 kinetics was proposed by Barstow and Molé (1987) after an original idea of Wasserman et al. (1974) refined by Whipp et al. (1982). This model foresees that an exponential increase in
kinetics was proposed by Barstow and Molé (1987) after an original idea of Wasserman et al. (1974) refined by Whipp et al. (1982). This model foresees that an exponential increase in 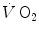 (phase II), related to metabolic adaptation in skeletal muscle, is preceded by a faster
(phase II), related to metabolic adaptation in skeletal muscle, is preceded by a faster 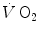 increase in the first seconds of exercise (phase I), which Barstow and Molé (1987) also treated as an exponential and which the British school led by Brian Whipp attributed to a rapid, also immediate cardiovascular response upon exercise onset (see, e.g. Whipp and Ward 1982, 1990). In the context of this model, the
increase in the first seconds of exercise (phase I), which Barstow and Molé (1987) also treated as an exponential and which the British school led by Brian Whipp attributed to a rapid, also immediate cardiovascular response upon exercise onset (see, e.g. Whipp and Ward 1982, 1990). In the context of this model, the 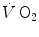 kinetics (measured value minus resting value) upon exercise onset is described by the following:
kinetics (measured value minus resting value) upon exercise onset is described by the following: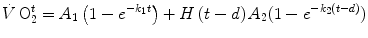
(3.5)
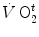 is the net
is the net 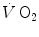 (measured value minus resting value) at time t, k 1 and k 2 are the velocity constants of the exponential
(measured value minus resting value) at time t, k 1 and k 2 are the velocity constants of the exponential 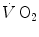 increase in phase I and II, respectively (their reciprocals τ 1 and τ 2 being the corresponding time constants), d is the time delay, and A 1 and A 2 are the amplitudes of the
increase in phase I and II, respectively (their reciprocals τ 1 and τ 2 being the corresponding time constants), d is the time delay, and A 1 and A 2 are the amplitudes of the 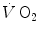 increase during phase I and phase II, respectively. H(t − d) is the associated Heaviside function, whose value is either 0 if t < d or 1 if t ≥ d.
increase during phase I and phase II, respectively. H(t − d) is the associated Heaviside function, whose value is either 0 if t < d or 1 if t ≥ d.Application of the double-exponential model to the analysis of the 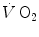 kinetics provides extremely rapid, functionally instantaneous τ 1 values, indicating a practically immediate upward translation of
kinetics provides extremely rapid, functionally instantaneous τ 1 values, indicating a practically immediate upward translation of 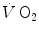 since the first breath. Higher τ 2 values are conversely obtained, similar to, although slightly faster than, the τ provided by the single-exponential model. This slight difference is a mere mathematical consequence of having introduced a time delay accounting for the time taken by venous blood to reach the pulmonary capillaries from the active muscles and thus corresponding to the time during which mixed venous oxygen concentration remains unchanged after exercise onset (Barstow and Molé 1987).
since the first breath. Higher τ 2 values are conversely obtained, similar to, although slightly faster than, the τ provided by the single-exponential model. This slight difference is a mere mathematical consequence of having introduced a time delay accounting for the time taken by venous blood to reach the pulmonary capillaries from the active muscles and thus corresponding to the time during which mixed venous oxygen concentration remains unchanged after exercise onset (Barstow and Molé 1987).
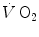 kinetics provides extremely rapid, functionally instantaneous τ 1 values, indicating a practically immediate upward translation of
kinetics provides extremely rapid, functionally instantaneous τ 1 values, indicating a practically immediate upward translation of 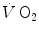 since the first breath. Higher τ 2 values are conversely obtained, similar to, although slightly faster than, the τ provided by the single-exponential model. This slight difference is a mere mathematical consequence of having introduced a time delay accounting for the time taken by venous blood to reach the pulmonary capillaries from the active muscles and thus corresponding to the time during which mixed venous oxygen concentration remains unchanged after exercise onset (Barstow and Molé 1987).
since the first breath. Higher τ 2 values are conversely obtained, similar to, although slightly faster than, the τ provided by the single-exponential model. This slight difference is a mere mathematical consequence of having introduced a time delay accounting for the time taken by venous blood to reach the pulmonary capillaries from the active muscles and thus corresponding to the time during which mixed venous oxygen concentration remains unchanged after exercise onset (Barstow and Molé 1987).The double-exponential model represents a significant refinement with respect to the single-exponential model, including also phenomena that are unrelated to muscle oxygen consumption kinetics. By so doing, Lador et al. (2006) obtained faster τ 2 values than previously reported for the muscle [PC] decrease (Binzoni et al. 1992; di Prampero et al. 2003; Rossiter et al. 1999), thus explicitly introducing the concept of a possible dissociation between lung oxygen uptake and muscle oxygen consumption also during light aerobic exercise.
This may be the case also for the kinetics of leg oxygen flow, which Grassi et al. (1996) analysed with a single-exponential model. In their study, however, the time constant of leg oxygen flow was found to be only slightly faster than that of the leg 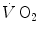 , but much slower than that of the muscle blood flow response at exercise onset, which is known to be extremely rapid (Rådegran and Saltin 1998; Toska and Ericksen 1994; Walloe and Wesche 1988). This data demonstrate that for some reasons, leg oxygen flow was unable to respond as fast as leg or muscle blood flow, suggesting that systemic oxygen flow, leg oxygen transfer and muscle oxygen consumption may be the consequence of different, independent, though optimized phenomena. Grassi et al. (1998) also demonstrated, on isolated–perfused dog gastrocnemii, that the time constant of the
, but much slower than that of the muscle blood flow response at exercise onset, which is known to be extremely rapid (Rådegran and Saltin 1998; Toska and Ericksen 1994; Walloe and Wesche 1988). This data demonstrate that for some reasons, leg oxygen flow was unable to respond as fast as leg or muscle blood flow, suggesting that systemic oxygen flow, leg oxygen transfer and muscle oxygen consumption may be the consequence of different, independent, though optimized phenomena. Grassi et al. (1998) also demonstrated, on isolated–perfused dog gastrocnemii, that the time constant of the 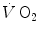 kinetics was the same in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease, further reinforcing the concept of an independent peripheral component of the kinetics of muscle oxygen consumption. This component, as discussed above, determines the net alactic oxygen deficit and is a necessary consequence of the mechanisms accelerating glycolysis at exercise onset.
kinetics was the same in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease, further reinforcing the concept of an independent peripheral component of the kinetics of muscle oxygen consumption. This component, as discussed above, determines the net alactic oxygen deficit and is a necessary consequence of the mechanisms accelerating glycolysis at exercise onset.
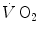 , but much slower than that of the muscle blood flow response at exercise onset, which is known to be extremely rapid (Rådegran and Saltin 1998; Toska and Ericksen 1994; Walloe and Wesche 1988). This data demonstrate that for some reasons, leg oxygen flow was unable to respond as fast as leg or muscle blood flow, suggesting that systemic oxygen flow, leg oxygen transfer and muscle oxygen consumption may be the consequence of different, independent, though optimized phenomena. Grassi et al. (1998) also demonstrated, on isolated–perfused dog gastrocnemii, that the time constant of the
, but much slower than that of the muscle blood flow response at exercise onset, which is known to be extremely rapid (Rådegran and Saltin 1998; Toska and Ericksen 1994; Walloe and Wesche 1988). This data demonstrate that for some reasons, leg oxygen flow was unable to respond as fast as leg or muscle blood flow, suggesting that systemic oxygen flow, leg oxygen transfer and muscle oxygen consumption may be the consequence of different, independent, though optimized phenomena. Grassi et al. (1998) also demonstrated, on isolated–perfused dog gastrocnemii, that the time constant of the 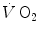 kinetics was the same in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease, further reinforcing the concept of an independent peripheral component of the kinetics of muscle oxygen consumption. This component, as discussed above, determines the net alactic oxygen deficit and is a necessary consequence of the mechanisms accelerating glycolysis at exercise onset.
kinetics was the same in conditions of normal and forced oxygen delivery and equal to that calculated for the kinetics of muscle phosphocreatine decrease, further reinforcing the concept of an independent peripheral component of the kinetics of muscle oxygen consumption. This component, as discussed above, determines the net alactic oxygen deficit and is a necessary consequence of the mechanisms accelerating glycolysis at exercise onset.Kinetics of Cardiac Output and Oxygen Delivery at Exercise Onset
The development of beat-by-beat techniques for the determination of cardiac output 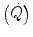 led to demonstrate that the kinetics of
led to demonstrate that the kinetics of 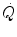 at exercise onset is very fast, much faster than that of
at exercise onset is very fast, much faster than that of 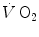 (Cummin et al. 1986; De Cort et al. 1991; Eriksen et al. 1990; Yoshida and Whipp 1994). Lador et al. (2006) modelled the kinetics of
(Cummin et al. 1986; De Cort et al. 1991; Eriksen et al. 1990; Yoshida and Whipp 1994). Lador et al. (2006) modelled the kinetics of 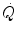 by extending the field of application of the dual exponential model of Barstow and Molé (1987) to include its description. During light aerobic exercise, they obtained very low τ values not only for phase I, but also for phase II (τ 2 equal to 2.1 s as compared to 15.4 s for
by extending the field of application of the dual exponential model of Barstow and Molé (1987) to include its description. During light aerobic exercise, they obtained very low τ values not only for phase I, but also for phase II (τ 2 equal to 2.1 s as compared to 15.4 s for 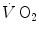 ). Since arterial oxygen concentration
). Since arterial oxygen concentration 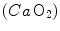 did not vary during the exercise transient in normoxia, the same was the case for systemic oxygen delivery
did not vary during the exercise transient in normoxia, the same was the case for systemic oxygen delivery 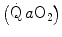
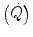 led to demonstrate that the kinetics of
led to demonstrate that the kinetics of 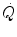 at exercise onset is very fast, much faster than that of
at exercise onset is very fast, much faster than that of 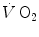 (Cummin et al. 1986; De Cort et al. 1991; Eriksen et al. 1990; Yoshida and Whipp 1994). Lador et al. (2006) modelled the kinetics of
(Cummin et al. 1986; De Cort et al. 1991; Eriksen et al. 1990; Yoshida and Whipp 1994). Lador et al. (2006) modelled the kinetics of 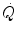 by extending the field of application of the dual exponential model of Barstow and Molé (1987) to include its description. During light aerobic exercise, they obtained very low τ values not only for phase I, but also for phase II (τ 2 equal to 2.1 s as compared to 15.4 s for
by extending the field of application of the dual exponential model of Barstow and Molé (1987) to include its description. During light aerobic exercise, they obtained very low τ values not only for phase I, but also for phase II (τ 2 equal to 2.1 s as compared to 15.4 s for 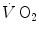 ). Since arterial oxygen concentration
). Since arterial oxygen concentration 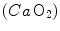 did not vary during the exercise transient in normoxia, the same was the case for systemic oxygen delivery
did not vary during the exercise transient in normoxia, the same was the case for systemic oxygen delivery 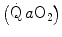
The rapid increase in 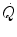 is the consequence of the equally rapid increase in heart rate (f H ) and in stroke volume (Q s). That the increase in f H is a very rapid phenomenon is a well-known concept since long. Fagraeus and Linnarsson (1976) identified two components of it, one almost immediate, the second slower and slightly delayed. They attributed the former to the withdrawal of vagal tone at exercise start, the latter to the progressive increase of sympathetic activity. Vagal blockade with atropine is known to suppress in fact the rapid component of the f H increase (Fagraeus and Linnarsson 1976). Coherently in hypoxia, when vagal activity is already reduced at rest, the amplitude of the f H increase in phase I is smaller than in normoxia (Lador et al. 2008).
is the consequence of the equally rapid increase in heart rate (f H ) and in stroke volume (Q s). That the increase in f H is a very rapid phenomenon is a well-known concept since long. Fagraeus and Linnarsson (1976) identified two components of it, one almost immediate, the second slower and slightly delayed. They attributed the former to the withdrawal of vagal tone at exercise start, the latter to the progressive increase of sympathetic activity. Vagal blockade with atropine is known to suppress in fact the rapid component of the f H increase (Fagraeus and Linnarsson 1976). Coherently in hypoxia, when vagal activity is already reduced at rest, the amplitude of the f H increase in phase I is smaller than in normoxia (Lador et al. 2008).
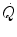 is the consequence of the equally rapid increase in heart rate (f H ) and in stroke volume (Q s). That the increase in f H is a very rapid phenomenon is a well-known concept since long. Fagraeus and Linnarsson (1976) identified two components of it, one almost immediate, the second slower and slightly delayed. They attributed the former to the withdrawal of vagal tone at exercise start, the latter to the progressive increase of sympathetic activity. Vagal blockade with atropine is known to suppress in fact the rapid component of the f H increase (Fagraeus and Linnarsson 1976). Coherently in hypoxia, when vagal activity is already reduced at rest, the amplitude of the f H increase in phase I is smaller than in normoxia (Lador et al. 2008).
is the consequence of the equally rapid increase in heart rate (f H ) and in stroke volume (Q s). That the increase in f H is a very rapid phenomenon is a well-known concept since long. Fagraeus and Linnarsson (1976) identified two components of it, one almost immediate, the second slower and slightly delayed. They attributed the former to the withdrawal of vagal tone at exercise start, the latter to the progressive increase of sympathetic activity. Vagal blockade with atropine is known to suppress in fact the rapid component of the f H increase (Fagraeus and Linnarsson 1976). Coherently in hypoxia, when vagal activity is already reduced at rest, the amplitude of the f H increase in phase I is smaller than in normoxia (Lador et al. 2008).The evidence concerning Q s is more elusive. The morphological evidence about heart innervation, indicating a presence of muscarinic receptors only in the sinus node, would suggest that vagal withdrawal would not act on Q s . This being the case, the 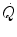 increase at exercise onset would be due only to the increase in f H . Yet a rapid increase in Q s was also demonstrated (Faisal et al. 2009; Lador et al. 2006, 2008), clearly opening the way to a possible role for the Frank-Starling mechanism in the Q s increase at exercise start, likely activated by the sudden blood displacement from lower limbs to the heart due to muscle pump action. If this is so, then
increase at exercise onset would be due only to the increase in f H . Yet a rapid increase in Q s was also demonstrated (Faisal et al. 2009; Lador et al. 2006, 2008), clearly opening the way to a possible role for the Frank-Starling mechanism in the Q s increase at exercise start, likely activated by the sudden blood displacement from lower limbs to the heart due to muscle pump action. If this is so, then 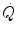 would be under dual control, neural (f H increase via vagal withdrawal) and mechanical (Q s increase via Frank-Starling mechanism).
would be under dual control, neural (f H increase via vagal withdrawal) and mechanical (Q s increase via Frank-Starling mechanism).
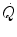 increase at exercise onset would be due only to the increase in f H . Yet a rapid increase in Q s was also demonstrated (Faisal et al. 2009; Lador et al. 2006, 2008), clearly opening the way to a possible role for the Frank-Starling mechanism in the Q s increase at exercise start, likely activated by the sudden blood displacement from lower limbs to the heart due to muscle pump action. If this is so, then
increase at exercise onset would be due only to the increase in f H . Yet a rapid increase in Q s was also demonstrated (Faisal et al. 2009; Lador et al. 2006, 2008), clearly opening the way to a possible role for the Frank-Starling mechanism in the Q s increase at exercise start, likely activated by the sudden blood displacement from lower limbs to the heart due to muscle pump action. If this is so, then 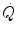 would be under dual control, neural (f H increase via vagal withdrawal) and mechanical (Q s increase via Frank-Starling mechanism).
would be under dual control, neural (f H increase via vagal withdrawal) and mechanical (Q s increase via Frank-Starling mechanism).The latter mechanism was proposed on the basis of animal studies (Sheriff et al. 1993), but direct evidence in healthy humans is still missing. Indirect evidence derives from experiments in supine posture, in which central blood volume is higher than in upright posture, showing that the phase I of 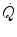 and Q s is not evident (Leyk et al. 1994; Wieling et al. 1996). In humans, the action of the Frank-Starling mechanism during exercise transients was clearly demonstrated only in heart transplant recipients, who do not show rapid f H increase at exercise start because they have denervated hearts (Meyer et al. 1994). Experiments with human exposure to lower body negative pressure would be crucial to further clarify this issue.
and Q s is not evident (Leyk et al. 1994; Wieling et al. 1996). In humans, the action of the Frank-Starling mechanism during exercise transients was clearly demonstrated only in heart transplant recipients, who do not show rapid f H increase at exercise start because they have denervated hearts (Meyer et al. 1994). Experiments with human exposure to lower body negative pressure would be crucial to further clarify this issue.
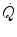 and Q s is not evident (Leyk et al. 1994; Wieling et al. 1996). In humans, the action of the Frank-Starling mechanism during exercise transients was clearly demonstrated only in heart transplant recipients, who do not show rapid f H increase at exercise start because they have denervated hearts (Meyer et al. 1994). Experiments with human exposure to lower body negative pressure would be crucial to further clarify this issue.
and Q s is not evident (Leyk et al. 1994; Wieling et al. 1996). In humans, the action of the Frank-Starling mechanism during exercise transients was clearly demonstrated only in heart transplant recipients, who do not show rapid f H increase at exercise start because they have denervated hearts (Meyer et al. 1994). Experiments with human exposure to lower body negative pressure would be crucial to further clarify this issue.A double-exponential treatment was already proposed for the kinetics of f H , but not for that of Q s . The use of an exponential model implies the assumption that the system behaves linearly. This may well be the case for f H , as indicated by the classical linear relationship between f H and power. This may not be so, however, for Q s , whose response to exercise steady state is markedly nonlinear (Cerretelli and di Prampero 1987). So, applying an exponential model to the analysis of Q s may be arbitrary. Lador et al. (2006) refrained from fitting parameters through Q s data for this reason. Under these circumstances, a tool for a quantitative evaluation of the contribution of Q s to the A 1 of 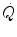 is provided by the following equation:
is provided by the following equation:
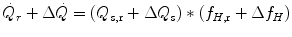
where suffix r designates the resting value of the corresponding variable, whereas Δ indicates the corresponding respective increments during phase I as compared with rest, which, assuming exponential models, should correspond to the respective phase I amplitudes (A 1). The use of Eq. (3.6), however, implies that ΔQ s would correspond to the A 1 of an exponential Q s increase only if the Q s kinetics upon exercise onset had the same time constant of the f H kinetics, which is still undemonstrated.
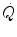 is provided by the following equation:
is provided by the following equation: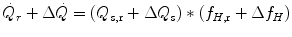
(3.6)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree