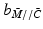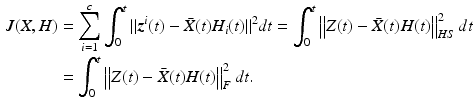, of ES signal ![$$\varvec{u} \in \mathscr {L}^m_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq2.gif) represents the electrical stimulation applied to the ith muscle. Since each array element does not necessarily correspond to a single muscle, we now introduce signal
represents the electrical stimulation applied to the ith muscle. Since each array element does not necessarily correspond to a single muscle, we now introduce signal ![$$\varvec{z} \in \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq3.gif) containing the stimulation applied to each of the n elements of the array over
containing the stimulation applied to each of the n elements of the array over ![$$t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq4.gif) . The stimulation provided to the ith muscle is assumed to be a linear combination of those array elements within spatial range, and hence can be modeled using the relationship
. The stimulation provided to the ith muscle is assumed to be a linear combination of those array elements within spatial range, and hence can be modeled using the relationship
![$$\begin{aligned} u_i(t) = \sum ^{n}_{j = 1} a_{i,j} z_j (t), \quad i = 1, \ldots , m, \quad t \in [0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ1.gif)
(8.1)
![$$\begin{aligned} M : \varvec{\varPhi } = H_{RB} F_m (\varvec{\varPhi },\dot{\varvec{\varPhi }}) H_{LAD} h_{IRC}(A \varvec{z}), \quad A :\varvec{z} \mapsto \varvec{u}: \varvec{u}(t) = \left[ \begin{array}{ccc} a_{1,1} &{}\cdots &{} a_{1,n} \\ \vdots &{}\ddots &{}\vdots \\ a_{m,1} &{}\cdots &{}a_{m,n} \end{array} \right] \varvec{z}(t) \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ2.gif)
(8.2)
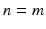 and
and 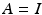 (i.e. each ES channel is associated with a single muscle).
(i.e. each ES channel is associated with a single muscle).It is possible to identify parameters in (8.2) by extending the approach developed in Chap. 2. However, in the case of the wrist and hand there are at least 41 musculo-tendon units actuating16 joints with 23 degrees of freedom [6]. This makes measurement of all joint angles and application and sensing of force/moments about each axis highly challenging. In addition, since the muscles are small and closely packed, the model system is sensitive to small changes in array position as well as to physiological changes such as fatigue and spasticity, and environmental conditions such as temperature and humidity. This makes the previous approach impractical, and therefore it will be exchanged for the identification of local linear models (as incorporated as an option within the design procedures of Chaps. 3, 4 and 6).
8.2 General Array Control Framework
Application of control design Procedure 4 of Sect. 6.4 to the array control problem first requires designing feedback controller K to stabilise the linearised model description 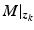 . The impractically of obtaining a global non-linear model means that we must identify
. The impractically of obtaining a global non-linear model means that we must identify 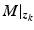 around each operating point
around each operating point 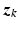 . The structure of
. The structure of 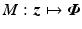 is given by (8.2) and has n inputs and p outputs, making it potentially high dimension. To recover a tractable identification problem we therefore embed a restricted plant stimulation space with dimension
is given by (8.2) and has n inputs and p outputs, making it potentially high dimension. To recover a tractable identification problem we therefore embed a restricted plant stimulation space with dimension 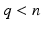 . From Definition 6.1, this necessitates feedback structure (6.11), and hence the control scheme takes the form shown in Fig. 8.1, where operator X is given by (6.6) with full rank
. From Definition 6.1, this necessitates feedback structure (6.11), and hence the control scheme takes the form shown in Fig. 8.1, where operator X is given by (6.6) with full rank 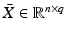 . We can expand the previous design procedure as follows:
. We can expand the previous design procedure as follows:
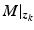 . The impractically of obtaining a global non-linear model means that we must identify
. The impractically of obtaining a global non-linear model means that we must identify 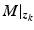 around each operating point
around each operating point 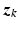 . The structure of
. The structure of 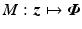 is given by (8.2) and has n inputs and p outputs, making it potentially high dimension. To recover a tractable identification problem we therefore embed a restricted plant stimulation space with dimension
is given by (8.2) and has n inputs and p outputs, making it potentially high dimension. To recover a tractable identification problem we therefore embed a restricted plant stimulation space with dimension 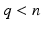 . From Definition 6.1, this necessitates feedback structure (6.11), and hence the control scheme takes the form shown in Fig. 8.1, where operator X is given by (6.6) with full rank
. From Definition 6.1, this necessitates feedback structure (6.11), and hence the control scheme takes the form shown in Fig. 8.1, where operator X is given by (6.6) with full rank 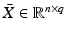 . We can expand the previous design procedure as follows:
. We can expand the previous design procedure as follows:Procedure 5
(Design for Robust stability: specification to electrode array)
Define task: Choose P via (6.1) and Lemma 6.3 to capture the required functional task (or for simplicity choose 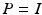 to track reference
to track reference 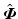 over
over ![$$t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq15.gif) ).
).
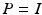 to track reference
to track reference 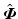 over
over ![$$t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq15.gif) ).
).Model identification: Apply input sequence 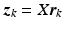 to the ES electrode array, and use resulting input-output data set
to the ES electrode array, and use resulting input-output data set 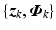 to identify a linear approximation to the dynamics
to identify a linear approximation to the dynamics 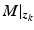 about
about 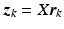 . Here
. Here
![$$\begin{aligned}&M |_{\varvec{z}(k)} : \mathscr {L}^n_2[0,T] \rightarrow \mathscr {L}^p_2[0,T] : \varvec{z} \mapsto \varvec{\varPhi } \nonumber \\&\,\;\;\;\;\;\qquad \qquad \qquad : \varvec{\varPhi } = \big ( H_{RB} |_{\varvec{w}} F_m (\varvec{\varPhi },\dot{\varvec{\varPhi }}) H_{LAD} \varvec{h}_{IRC} (A \varvec{z}) \big ) |_{\varvec{z}_k} \varvec{z} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ3.gif)
Feedback controller design: Design ![$$K_X : \mathscr {L}^p_2[0,T] \rightarrow \mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq20.gif) to stabilize
to stabilize 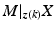 . This is equivalent to designing K to stabilize
. This is equivalent to designing K to stabilize 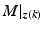 given structure (6.11).
given structure (6.11).
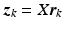 to the ES electrode array, and use resulting input-output data set
to the ES electrode array, and use resulting input-output data set 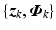 to identify a linear approximation to the dynamics
to identify a linear approximation to the dynamics 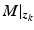 about
about 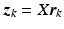 . Here
. Here![$$\begin{aligned}&M |_{\varvec{z}(k)} : \mathscr {L}^n_2[0,T] \rightarrow \mathscr {L}^p_2[0,T] : \varvec{z} \mapsto \varvec{\varPhi } \nonumber \\&\,\;\;\;\;\;\qquad \qquad \qquad : \varvec{\varPhi } = \big ( H_{RB} |_{\varvec{w}} F_m (\varvec{\varPhi },\dot{\varvec{\varPhi }}) H_{LAD} \varvec{h}_{IRC} (A \varvec{z}) \big ) |_{\varvec{z}_k} \varvec{z} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ3.gif)
(8.3)
![$$K_X : \mathscr {L}^p_2[0,T] \rightarrow \mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq20.gif) to stabilize
to stabilize 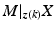 . This is equivalent to designing K to stabilize
. This is equivalent to designing K to stabilize 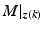 given structure (6.11).
given structure (6.11).ILC design: Design L to satisfy condition (6.14) or (6.17) of Theorem 6.1 for the resulting closed-loop system
![$$\begin{aligned}&G |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} : \mathscr {L}^p_2[0,T] \rightarrow \mathscr {L}^p_2[0,T] : \varvec{v} \mapsto \varvec{\varPhi } : \varvec{\varPhi } = (I + M |_{\varvec{z}(k)} K)^{-1} M |_{\varvec{z}(k)} K \varvec{v}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ4.gif)
The first condition guarantees nominal convergence to zero error, but requires 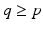 . In both cases, implement ILC update using (6.26).
. In both cases, implement ILC update using (6.26).
![$$\begin{aligned}&G |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} : \mathscr {L}^p_2[0,T] \rightarrow \mathscr {L}^p_2[0,T] : \varvec{v} \mapsto \varvec{\varPhi } : \varvec{\varPhi } = (I + M |_{\varvec{z}(k)} K)^{-1} M |_{\varvec{z}(k)} K \varvec{v}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ4.gif)
(8.4)
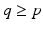 . In both cases, implement ILC update using (6.26).
. In both cases, implement ILC update using (6.26).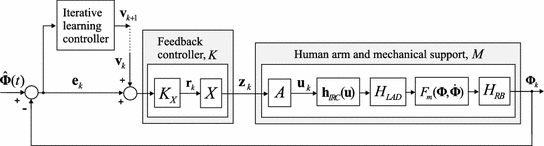
Fig. 8.1
Feedback and ILC control scheme specified to electrode array structure
We next present examples of explicit forms of 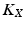 and L for application in the above procedure. These assume that the form of linearized system (8.3) is stipulated by the designer as a static
and L for application in the above procedure. These assume that the form of linearized system (8.3) is stipulated by the designer as a static 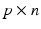 mapping, i.e. with form
mapping, i.e. with form
![$$\begin{aligned} F : \mathscr {L}^n[0,T] \rightarrow \mathscr {L}^p[0,T] : \varvec{z} \mapsto \varvec{\varPhi } : \varvec{\varPhi }(t) = \bar{F} \varvec{z}(t), \;\; \bar{F} \in \mathbb {R}^{p \times n}, \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ5.gif)
followed by SISO linear dynamics. In practice this assumption is supported by similar muscle and rigid body dynamics in the wrist and hand, together with the presence of spasticity, inherent stiffness, and the low bandwidth of required movements.
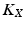 and L for application in the above procedure. These assume that the form of linearized system (8.3) is stipulated by the designer as a static
and L for application in the above procedure. These assume that the form of linearized system (8.3) is stipulated by the designer as a static 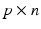 mapping, i.e. with form
mapping, i.e. with form![$$\begin{aligned} F : \mathscr {L}^n[0,T] \rightarrow \mathscr {L}^p[0,T] : \varvec{z} \mapsto \varvec{\varPhi } : \varvec{\varPhi }(t) = \bar{F} \varvec{z}(t), \;\; \bar{F} \in \mathbb {R}^{p \times n}, \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ5.gif)
(8.5)
Proposition 8.1
Let linearized dynamics (8.3) have form 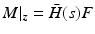 where F is given by (8.5) and
where F is given by (8.5) and 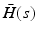 is a SISO system. The feedback control action
is a SISO system. The feedback control action 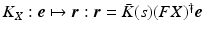 , where
, where 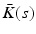 is a SISO system, applied to system
is a SISO system, applied to system 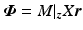 realizes stimulation input
realizes stimulation input
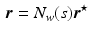
where 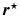 is the unique minimizer of a weighted norm of the tracking error,
is the unique minimizer of a weighted norm of the tracking error, 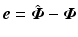 , and the SISO system
, and the SISO system
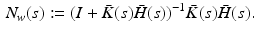
The resulting closed-loop system dynamics are
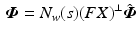
where the orthogonal projection onto the range of FX is 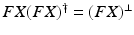 ,
,
![$$\begin{aligned} (FX)^\perp : \mathscr {L}^p[0,T] \rightarrow \mathscr {L}^p[0,T] : \hat{\varvec{\varPhi }} \mapsto \varvec{x} : \varvec{x}(t) = \bar{F} \bar{X}(\bar{F} \bar{X})^\dagger \hat{\varvec{\varPhi }}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ9.gif)
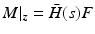 where F is given by (8.5) and
where F is given by (8.5) and 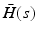 is a SISO system. The feedback control action
is a SISO system. The feedback control action 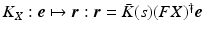 , where
, where 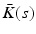 is a SISO system, applied to system
is a SISO system, applied to system 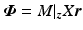 realizes stimulation input
realizes stimulation input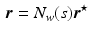
(8.6)
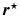 is the unique minimizer of a weighted norm of the tracking error,
is the unique minimizer of a weighted norm of the tracking error, 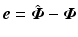 , and the SISO system
, and the SISO system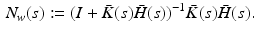
(8.7)
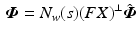
(8.8)
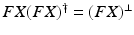 ,
,![$$\begin{aligned} (FX)^\perp : \mathscr {L}^p[0,T] \rightarrow \mathscr {L}^p[0,T] : \hat{\varvec{\varPhi }} \mapsto \varvec{x} : \varvec{x}(t) = \bar{F} \bar{X}(\bar{F} \bar{X})^\dagger \hat{\varvec{\varPhi }}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ9.gif)
(8.9)
Proof
Consider the weighted tracking error 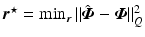 where weight
where weight 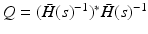 with
with 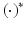 the adjoint operator. This has solution
the adjoint operator. This has solution
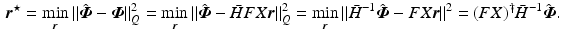 The proposed control action
The proposed control action 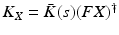 realizes (when
realizes (when  )
)
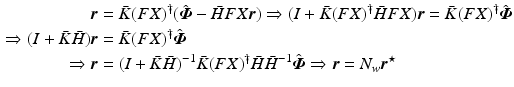
The corresponding closed-loop dynamics are
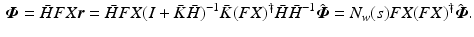
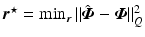 where weight
where weight 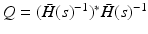 with
with 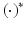 the adjoint operator. This has solution
the adjoint operator. This has solution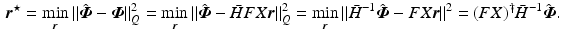
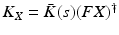 realizes (when
realizes (when  )
)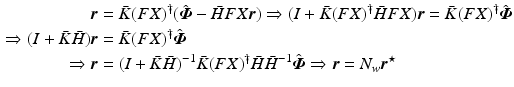
(8.10)
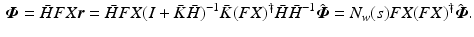
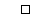
The feedback control action 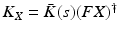 of Proposition 8.1 therefore ensures that
of Proposition 8.1 therefore ensures that 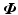 tracks the demand input
tracks the demand input 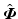 (or
(or 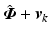 if ILC is also applied) as closely as possible, subject to dynamics
if ILC is also applied) as closely as possible, subject to dynamics 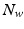 specified by the designer. It requires only that SISO feedback controller
specified by the designer. It requires only that SISO feedback controller 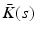 be selected to stabilize dynamics (8.7), but has the property of stabilizing all p joints. By enforcing dynamics
be selected to stabilize dynamics (8.7), but has the property of stabilizing all p joints. By enforcing dynamics 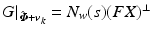 , it also facilitates the following simplified ILC update:
, it also facilitates the following simplified ILC update:
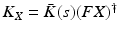 of Proposition 8.1 therefore ensures that
of Proposition 8.1 therefore ensures that 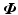 tracks the demand input
tracks the demand input 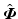 (or
(or 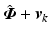 if ILC is also applied) as closely as possible, subject to dynamics
if ILC is also applied) as closely as possible, subject to dynamics 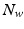 specified by the designer. It requires only that SISO feedback controller
specified by the designer. It requires only that SISO feedback controller 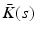 be selected to stabilize dynamics (8.7), but has the property of stabilizing all p joints. By enforcing dynamics
be selected to stabilize dynamics (8.7), but has the property of stabilizing all p joints. By enforcing dynamics 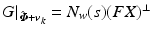 , it also facilitates the following simplified ILC update:
, it also facilitates the following simplified ILC update:Proposition 8.2
The system of Fig. 8.1 with 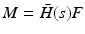 , the feedback action of Proposition 8.1, and ILC update
, the feedback action of Proposition 8.1, and ILC update
![$$\begin{aligned} \varvec{v}_{k+1} = \varvec{v}_{k} + L P \varvec{e}_{k}, \quad L = l (P N_w (F X)^\perp )^\dagger , \quad l \in (0,1] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ11.gif)
satisfies (6.17) and enforces convergence to the minimum extended error norm, i.e.
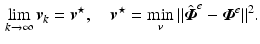
Furthermore, if 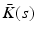 is tuned so that
is tuned so that 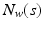 approximates a pure delay of
approximates a pure delay of 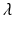 seconds then (8.11) corresponds to the phaselead update
seconds then (8.11) corresponds to the phaselead update
![$$\begin{aligned} \varvec{v}_{k+1}(t) = \varvec{v}_{k}(t) + l (P_j (\bar{F} \bar{X})^\perp )^\dagger \varvec{e}_k^e (t + \lambda ), \quad \quad t \in [t_{j-1},t_j], \; j = 1, \ldots S. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ13.gif)
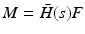 , the feedback action of Proposition 8.1, and ILC update
, the feedback action of Proposition 8.1, and ILC update![$$\begin{aligned} \varvec{v}_{k+1} = \varvec{v}_{k} + L P \varvec{e}_{k}, \quad L = l (P N_w (F X)^\perp )^\dagger , \quad l \in (0,1] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ11.gif)
(8.11)
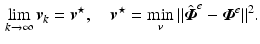
(8.12)
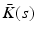 is tuned so that
is tuned so that 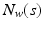 approximates a pure delay of
approximates a pure delay of 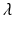 seconds then (8.11) corresponds to the phaselead update
seconds then (8.11) corresponds to the phaselead update![$$\begin{aligned} \varvec{v}_{k+1}(t) = \varvec{v}_{k}(t) + l (P_j (\bar{F} \bar{X})^\perp )^\dagger \varvec{e}_k^e (t + \lambda ), \quad \quad t \in [t_{j-1},t_j], \; j = 1, \ldots S. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ13.gif)
(8.13)
Proof
We set 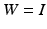 in Theorem 6.1 and assume
in Theorem 6.1 and assume 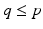 . Since Proposition 8.1 yields closed-loop dynamics
. Since Proposition 8.1 yields closed-loop dynamics 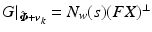 , we then substitute
, we then substitute 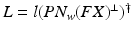 and
and 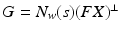 into
into 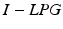 to give
to give 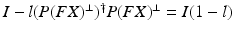 which satisfies (6.17). The corresponding limiting error solution (6.22),
which satisfies (6.17). The corresponding limiting error solution (6.22), 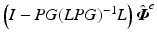 , is given by
, is given by 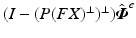 which is the orthogonal projection onto the kernel of
which is the orthogonal projection onto the kernel of 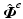 . This is the minimum achievable error and hence solves (8.12). If
. This is the minimum achievable error and hence solves (8.12). If 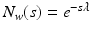 then
then 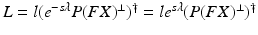 with time-based implementation (8.13).
with time-based implementation (8.13). 
 in Theorem 6.1 and assume
in Theorem 6.1 and assume 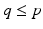 . Since Proposition 8.1 yields closed-loop dynamics
. Since Proposition 8.1 yields closed-loop dynamics 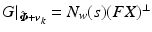 , we then substitute
, we then substitute 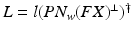 and
and 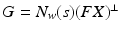 into
into 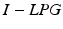 to give
to give 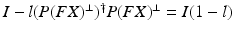 which satisfies (6.17). The corresponding limiting error solution (6.22),
which satisfies (6.17). The corresponding limiting error solution (6.22), 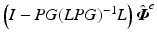 , is given by
, is given by 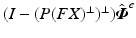 which is the orthogonal projection onto the kernel of
which is the orthogonal projection onto the kernel of 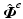 . This is the minimum achievable error and hence solves (8.12). If
. This is the minimum achievable error and hence solves (8.12). If 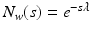 then
then 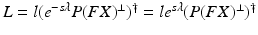 with time-based implementation (8.13).
with time-based implementation (8.13). 
Note that update (8.13) takes the ‘phase-lead ILC’ form, which has received significant research attention due to its simple structure (with only two parameters, l, 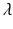 ) that enables heuristic tuning [7–9].
) that enables heuristic tuning [7–9].
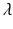 ) that enables heuristic tuning [7–9].
) that enables heuristic tuning [7–9].We next examine how stimulation subspace X can be chosen to balance tracking accuracy with practicality of identification.
8.3 Subspace Identification
The identification of subspace 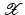 is addressed in this section, with subsequent identification of the q input, p output system
is addressed in this section, with subsequent identification of the q input, p output system 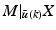 following in Sect. 8.4. The purpose of
following in Sect. 8.4. The purpose of 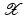 is to reduce the dimension of the latter problem so that it can feasibly be performed within the limited time available in practice. The use of
is to reduce the dimension of the latter problem so that it can feasibly be performed within the limited time available in practice. The use of 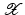 is motivated by the observation that only a subset of muscles are required for a given posture, and the underlying muscle locations can be assumed to not change. It is hence possible to select an input subspace that covers those muscles needed to perform a required set of tasks, together with the possible variation in array placement. In practice a suitable input subspace can be constructed using:
is motivated by the observation that only a subset of muscles are required for a given posture, and the underlying muscle locations can be assumed to not change. It is hence possible to select an input subspace that covers those muscles needed to perform a required set of tasks, together with the possible variation in array placement. In practice a suitable input subspace can be constructed using:
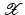 is addressed in this section, with subsequent identification of the q input, p output system
is addressed in this section, with subsequent identification of the q input, p output system 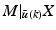 following in Sect. 8.4. The purpose of
following in Sect. 8.4. The purpose of 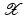 is to reduce the dimension of the latter problem so that it can feasibly be performed within the limited time available in practice. The use of
is to reduce the dimension of the latter problem so that it can feasibly be performed within the limited time available in practice. The use of 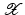 is motivated by the observation that only a subset of muscles are required for a given posture, and the underlying muscle locations can be assumed to not change. It is hence possible to select an input subspace that covers those muscles needed to perform a required set of tasks, together with the possible variation in array placement. In practice a suitable input subspace can be constructed using:
is motivated by the observation that only a subset of muscles are required for a given posture, and the underlying muscle locations can be assumed to not change. It is hence possible to select an input subspace that covers those muscles needed to perform a required set of tasks, together with the possible variation in array placement. In practice a suitable input subspace can be constructed using:
previous experimental input and output data, and/or
structural information based on prior system knowledge.
From the comments made following Theorem 6.3, any basis can be used to define the stimulation subspace without affecting subsequent performance (i.e. X may be exchanged for 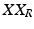 with any full rank
with any full rank 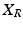 ).
).
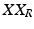 with any full rank
with any full rank 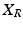 ).
).8.3.1 Selection Using Experimental Data
Assume that previous experiments (with any choice of input subspace) have yielded input and output signal pairs 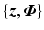 for plant M given by (8.2) (where
for plant M given by (8.2) (where 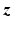 is the stimulation applied to the n elements of the array). From these select those with outputs close to the required movement(s), and denote as
is the stimulation applied to the n elements of the array). From these select those with outputs close to the required movement(s), and denote as 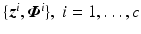 . These can be used to produce a basis for the input set by directly inserting in X as
. These can be used to produce a basis for the input set by directly inserting in X as
![$$\begin{aligned} \bar{X}(t) = [\varvec{z}^1(t), \varvec{z}^2(t), \dots , \varvec{z}^c(t)] \in \mathbb {R}^{n \times c} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ14.gif)
and setting 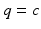 . If X is time-invariant, then a finite set of
. If X is time-invariant, then a finite set of 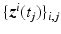 can instead be employed. In the case of linear M, any reference in the set spanned by a linear combination of
can instead be employed. In the case of linear M, any reference in the set spanned by a linear combination of 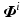 (corresponding to the range of MX,
(corresponding to the range of MX, 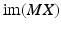 ), will be tracked with zero error using the ILC algorithms of Theorem 6.1. If
), will be tracked with zero error using the ILC algorithms of Theorem 6.1. If 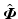 does not belong to this set, then the subsequent error is the orthogonal projection of
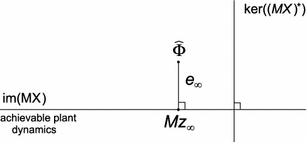
does not belong to this set, then the subsequent error is the orthogonal projection of 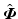 onto
onto 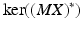 , as shown in Fig. 8.2. If
, as shown in Fig. 8.2. If 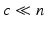 , the dimension of MX is far smaller than that of M. The direct use of previous inputs is not ideal as q cannot be independently prescribed (since
, the dimension of MX is far smaller than that of M. The direct use of previous inputs is not ideal as q cannot be independently prescribed (since 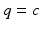 ). Inputs may also be linearly dependent, and thereby provide no new information. This is now addressed.
). Inputs may also be linearly dependent, and thereby provide no new information. This is now addressed.
 for plant M given by (8.2) (where
for plant M given by (8.2) (where 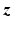 is the stimulation applied to the n elements of the array). From these select those with outputs close to the required movement(s), and denote as
is the stimulation applied to the n elements of the array). From these select those with outputs close to the required movement(s), and denote as 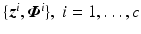 . These can be used to produce a basis for the input set by directly inserting in X as
. These can be used to produce a basis for the input set by directly inserting in X as![$$\begin{aligned} \bar{X}(t) = [\varvec{z}^1(t), \varvec{z}^2(t), \dots , \varvec{z}^c(t)] \in \mathbb {R}^{n \times c} \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ14.gif)
(8.14)
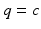 . If X is time-invariant, then a finite set of
. If X is time-invariant, then a finite set of 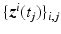 can instead be employed. In the case of linear M, any reference in the set spanned by a linear combination of
can instead be employed. In the case of linear M, any reference in the set spanned by a linear combination of 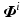 (corresponding to the range of MX,
(corresponding to the range of MX, 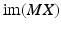 ), will be tracked with zero error using the ILC algorithms of Theorem 6.1. If
), will be tracked with zero error using the ILC algorithms of Theorem 6.1. If 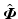 does not belong to this set, then the subsequent error is the orthogonal projection of
does not belong to this set, then the subsequent error is the orthogonal projection of 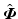 onto
onto 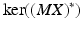 , as shown in Fig. 8.2. If
, as shown in Fig. 8.2. If 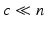 , the dimension of MX is far smaller than that of M. The direct use of previous inputs is not ideal as q cannot be independently prescribed (since
, the dimension of MX is far smaller than that of M. The direct use of previous inputs is not ideal as q cannot be independently prescribed (since 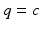 ). Inputs may also be linearly dependent, and thereby provide no new information. This is now addressed.
). Inputs may also be linearly dependent, and thereby provide no new information. This is now addressed.
Fig. 8.2
Output space showing error as an orthogonal projection onto achievable plant dynamics
8.3.1.1 Previous Input Data
Let subspace dimension q be prescribed and data sets 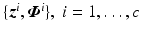 available. The next proposition provides optimizations to yield
available. The next proposition provides optimizations to yield ![$$X : \mathscr {L}^q_2[0,T] \rightarrow \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq85.gif) :
:
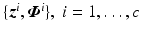 available. The next proposition provides optimizations to yield
available. The next proposition provides optimizations to yield ![$$X : \mathscr {L}^q_2[0,T] \rightarrow \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq85.gif) :
:Proposition 8.3
The distance between each ![$$\varvec{z}^i \in \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq86.gif) and the closest element in the image of X is minimized by solving
and the closest element in the image of X is minimized by solving
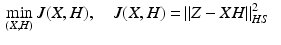
where 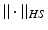 is the Hilbert-Schmidt norm and operators
is the Hilbert-Schmidt norm and operators
![$$\begin{aligned} H&: \mathbb {R}^c \rightarrow \mathscr {L}^q_2[0,T] : \varvec{a} \mapsto \varvec{b} : \varvec{b}_i = \sum ^c_{i = 1} H_i \varvec{a}_i, \nonumber \\ Z&: \mathbb {R}^c \rightarrow \mathscr {L}^n_2[0,T] : \varvec{a} \mapsto \varvec{b} : \varvec{b}_i = \sum ^c_{i = 1} \varvec{z}^i \varvec{a}_i. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ16.gif)
Using the Frobenius norm 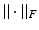 , this can also be expressed as
, this can also be expressed as
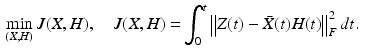
![$$\varvec{z}^i \in \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq86.gif) and the closest element in the image of X is minimized by solving
and the closest element in the image of X is minimized by solving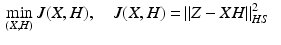
(8.15)
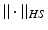 is the Hilbert-Schmidt norm and operators
is the Hilbert-Schmidt norm and operators![$$\begin{aligned} H&: \mathbb {R}^c \rightarrow \mathscr {L}^q_2[0,T] : \varvec{a} \mapsto \varvec{b} : \varvec{b}_i = \sum ^c_{i = 1} H_i \varvec{a}_i, \nonumber \\ Z&: \mathbb {R}^c \rightarrow \mathscr {L}^n_2[0,T] : \varvec{a} \mapsto \varvec{b} : \varvec{b}_i = \sum ^c_{i = 1} \varvec{z}^i \varvec{a}_i. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ16.gif)
(8.16)
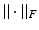 , this can also be expressed as
, this can also be expressed as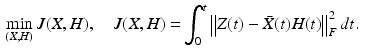
(8.17)
Proof
The total distance between each ![$$\varvec{z}^i \in \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq89.gif) and the closest element in the image of
and the closest element in the image of
![$$\begin{aligned} X : \mathscr {L}^q_2[0,T] \rightarrow \mathscr {L}^n_2[0,T] : \varvec{r} \mapsto \varvec{z} : \varvec{z}(t) = \bar{X}(t) \varvec{r}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ18.gif)
is minimized by solving
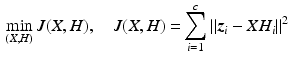
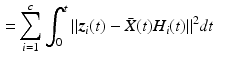
where ![$$H_i \in \mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq90.gif) . This is simplified by using
. This is simplified by using
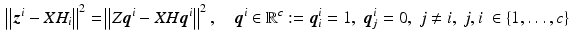 since
since 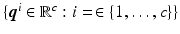 is an orthogonal basis of
is an orthogonal basis of 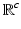 , it follows that
, it follows that
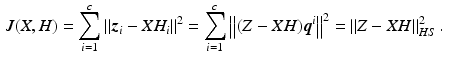
Note, from (8.20), that this can also be expressed as
![$$\varvec{z}^i \in \mathscr {L}^n_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq89.gif) and the closest element in the image of
and the closest element in the image of![$$\begin{aligned} X : \mathscr {L}^q_2[0,T] \rightarrow \mathscr {L}^n_2[0,T] : \varvec{r} \mapsto \varvec{z} : \varvec{z}(t) = \bar{X}(t) \varvec{r}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_Equ18.gif)
(8.18)
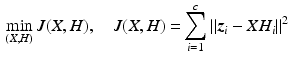
(8.19)
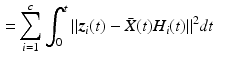
(8.20)
![$$H_i \in \mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_8_Chapter_IEq90.gif) . This is simplified by using
. This is simplified by using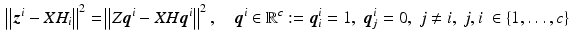
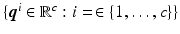 is an orthogonal basis of
is an orthogonal basis of 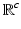 , it follows that
, it follows that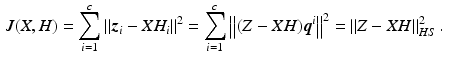
(8.21)