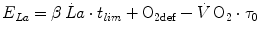, Critical Power and Maximal Aerobic Power
Abstract
The critical power ( ) is the highest power that can be sustained relying exclusively on aerobic metabolism, although unevenly distributed among muscle fibres, and thus, it is the highest power for which oxygen consumption is, not only in theory, the sole source of metabolic energy. As such, the
) is the highest power that can be sustained relying exclusively on aerobic metabolism, although unevenly distributed among muscle fibres, and thus, it is the highest power for which oxygen consumption is, not only in theory, the sole source of metabolic energy. As such, the  concept is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state and for its association to the maximal lactate steady state. The
concept is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state and for its association to the maximal lactate steady state. The  corresponds to the y-axis asymptote of the hyperbolic relationship between sustained power and time to exhaustion. The curvature of the hyperbole defines a constant corresponding to the amount of mechanical work that can be sustained above the
corresponds to the y-axis asymptote of the hyperbolic relationship between sustained power and time to exhaustion. The curvature of the hyperbole defines a constant corresponding to the amount of mechanical work that can be sustained above the 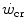 (energy store component). The energy store component does not correspond to the anaerobic capacity, but to the amount of work that can be carried out at powers higher than the
(energy store component). The energy store component does not correspond to the anaerobic capacity, but to the amount of work that can be carried out at powers higher than the 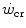 , the energy sustaining it deriving from both aerobic and anaerobic sources. After a survey of the descriptive physiology of
, the energy sustaining it deriving from both aerobic and anaerobic sources. After a survey of the descriptive physiology of 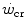 , the case of intermittent exercise is discussed, as is the relationship between
, the case of intermittent exercise is discussed, as is the relationship between 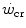 and the maximal aerobic power. Finally, the three-parameter model of
and the maximal aerobic power. Finally, the three-parameter model of 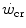 , taken as an example of generalization, is considered, evidencing the relation between its y-axis intercept and the maximal instantaneous anaerobic alactic power. The determination of
, taken as an example of generalization, is considered, evidencing the relation between its y-axis intercept and the maximal instantaneous anaerobic alactic power. The determination of 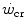 is a key issue in exercise testing. Procedures for simplifying its determination have been proposed.
is a key issue in exercise testing. Procedures for simplifying its determination have been proposed.
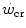 ) is the highest power that can be sustained relying exclusively on aerobic metabolism, although unevenly distributed among muscle fibres, and thus, it is the highest power for which oxygen consumption is, not only in theory, the sole source of metabolic energy. As such, the
) is the highest power that can be sustained relying exclusively on aerobic metabolism, although unevenly distributed among muscle fibres, and thus, it is the highest power for which oxygen consumption is, not only in theory, the sole source of metabolic energy. As such, the 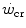 concept is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state and for its association to the maximal lactate steady state. The
concept is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state and for its association to the maximal lactate steady state. The 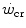 corresponds to the y-axis asymptote of the hyperbolic relationship between sustained power and time to exhaustion. The curvature of the hyperbole defines a constant corresponding to the amount of mechanical work that can be sustained above the
corresponds to the y-axis asymptote of the hyperbolic relationship between sustained power and time to exhaustion. The curvature of the hyperbole defines a constant corresponding to the amount of mechanical work that can be sustained above the 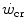 (energy store component). The energy store component does not correspond to the anaerobic capacity, but to the amount of work that can be carried out at powers higher than the
(energy store component). The energy store component does not correspond to the anaerobic capacity, but to the amount of work that can be carried out at powers higher than the 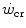 , the energy sustaining it deriving from both aerobic and anaerobic sources. After a survey of the descriptive physiology of
, the energy sustaining it deriving from both aerobic and anaerobic sources. After a survey of the descriptive physiology of 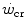 , the case of intermittent exercise is discussed, as is the relationship between
, the case of intermittent exercise is discussed, as is the relationship between 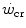 and the maximal aerobic power. Finally, the three-parameter model of
and the maximal aerobic power. Finally, the three-parameter model of 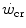 , taken as an example of generalization, is considered, evidencing the relation between its y-axis intercept and the maximal instantaneous anaerobic alactic power. The determination of
, taken as an example of generalization, is considered, evidencing the relation between its y-axis intercept and the maximal instantaneous anaerobic alactic power. The determination of 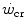 is a key issue in exercise testing. Procedures for simplifying its determination have been proposed.
is a key issue in exercise testing. Procedures for simplifying its determination have been proposed.Introduction
The concept of critical power (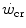 ) is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state. The
) is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state. The 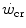 was firstly defined by Monod and Scherrer (1965) as “the maximum power that can be kept up for a very long time without fatigue”. This qualitative definition came nevertheless from the quantitative analysis of a graph, in which they plotted the total work done, determined during several fatiguing exercise bouts of variable intensity, as a function of the exhaustion time. They gave a hyperbolic solution to this plot, where
was firstly defined by Monod and Scherrer (1965) as “the maximum power that can be kept up for a very long time without fatigue”. This qualitative definition came nevertheless from the quantitative analysis of a graph, in which they plotted the total work done, determined during several fatiguing exercise bouts of variable intensity, as a function of the exhaustion time. They gave a hyperbolic solution to this plot, where 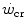 corresponds to the dependent variable’s asymptote (Fig. 5.1), while the curvature of the hyperbole [the product of x times (
corresponds to the dependent variable’s asymptote (Fig. 5.1), while the curvature of the hyperbole [the product of x times (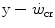 )] defines a constant corresponding to the amount of mechanical work that can be sustained above
)] defines a constant corresponding to the amount of mechanical work that can be sustained above 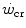 , which was called the “energy store” component (W′). This relationship can be linearized by replacing time with its reciprocal as independent variable, in which case the
, which was called the “energy store” component (W′). This relationship can be linearized by replacing time with its reciprocal as independent variable, in which case the 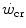 is the y-axis intercept and W′ is the line’s slope.
is the y-axis intercept and W′ is the line’s slope.
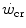 ) is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state. The
) is fundamental in exercise physiology for its strict relation to the concept of metabolic steady state. The 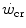 was firstly defined by Monod and Scherrer (1965) as “the maximum power that can be kept up for a very long time without fatigue”. This qualitative definition came nevertheless from the quantitative analysis of a graph, in which they plotted the total work done, determined during several fatiguing exercise bouts of variable intensity, as a function of the exhaustion time. They gave a hyperbolic solution to this plot, where
was firstly defined by Monod and Scherrer (1965) as “the maximum power that can be kept up for a very long time without fatigue”. This qualitative definition came nevertheless from the quantitative analysis of a graph, in which they plotted the total work done, determined during several fatiguing exercise bouts of variable intensity, as a function of the exhaustion time. They gave a hyperbolic solution to this plot, where 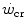 corresponds to the dependent variable’s asymptote (Fig. 5.1), while the curvature of the hyperbole [the product of x times (
corresponds to the dependent variable’s asymptote (Fig. 5.1), while the curvature of the hyperbole [the product of x times (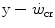 )] defines a constant corresponding to the amount of mechanical work that can be sustained above
)] defines a constant corresponding to the amount of mechanical work that can be sustained above 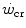 , which was called the “energy store” component (W′). This relationship can be linearized by replacing time with its reciprocal as independent variable, in which case the
, which was called the “energy store” component (W′). This relationship can be linearized by replacing time with its reciprocal as independent variable, in which case the 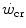 is the y-axis intercept and W′ is the line’s slope.
is the y-axis intercept and W′ is the line’s slope.
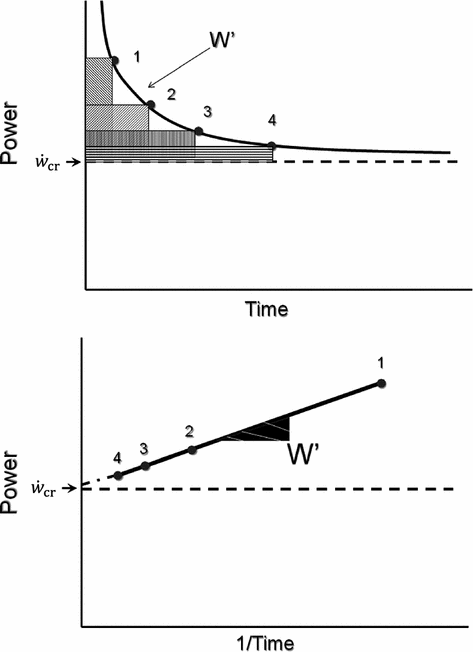
Fig. 5.1
Top panel Schematic qualitative representation showing the power versus time relationship for high-intensity exercise. Points 1–4 indicate the time to exhaustion for independent tests at the designated power. The critical power (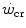 ) is the y-axis asymptote of the hyperbola. Bottom panel Schematic qualitative representation showing the linearized version of the power versus time relationship, obtained by replacing time by its reciprocal. Points 1–4 indicate the time to exhaustion for independent tests at the designated power, as in the top panel. The
) is the y-axis asymptote of the hyperbola. Bottom panel Schematic qualitative representation showing the linearized version of the power versus time relationship, obtained by replacing time by its reciprocal. Points 1–4 indicate the time to exhaustion for independent tests at the designated power, as in the top panel. The 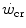 is the y-axis intercept of the line. In both graphs, W′ is the mechanical work above
is the y-axis intercept of the line. In both graphs, W′ is the mechanical work above 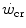 : it corresponds to the hyperbola’s curvature in the top panel and to the line’s slope in the bottom graph. Modified after Jones et al. (2010)
: it corresponds to the hyperbola’s curvature in the top panel and to the line’s slope in the bottom graph. Modified after Jones et al. (2010)
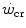 ) is the y-axis asymptote of the hyperbola. Bottom panel Schematic qualitative representation showing the linearized version of the power versus time relationship, obtained by replacing time by its reciprocal. Points 1–4 indicate the time to exhaustion for independent tests at the designated power, as in the top panel. The
) is the y-axis asymptote of the hyperbola. Bottom panel Schematic qualitative representation showing the linearized version of the power versus time relationship, obtained by replacing time by its reciprocal. Points 1–4 indicate the time to exhaustion for independent tests at the designated power, as in the top panel. The 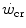 is the y-axis intercept of the line. In both graphs, W′ is the mechanical work above
is the y-axis intercept of the line. In both graphs, W′ is the mechanical work above 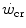 : it corresponds to the hyperbola’s curvature in the top panel and to the line’s slope in the bottom graph. Modified after Jones et al. (2010)
: it corresponds to the hyperbola’s curvature in the top panel and to the line’s slope in the bottom graph. Modified after Jones et al. (2010)Monod and Scherrer (1965) considered 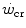 dependent, at least in part, on muscle blood flow and hence oxygen delivery. Moritani et al. (1981) associated
dependent, at least in part, on muscle blood flow and hence oxygen delivery. Moritani et al. (1981) associated 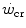 with the lactate threshold. Although it has become clear that
with the lactate threshold. Although it has become clear that 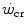 is a higher power than that corresponding to the lactate threshold, at least in non-athletic individuals (Poole et al. 1988, 1990), this may be the case in endurance athletes (Jones and Poole 2009), who are characterized by an elevated fraction of type I slow aerobic fibres in locomotory muscles as compared to the former. Subsequent studies have related W′ to overall anaerobic capacity and
is a higher power than that corresponding to the lactate threshold, at least in non-athletic individuals (Poole et al. 1988, 1990), this may be the case in endurance athletes (Jones and Poole 2009), who are characterized by an elevated fraction of type I slow aerobic fibres in locomotory muscles as compared to the former. Subsequent studies have related W′ to overall anaerobic capacity and 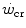 to the power sustained in evenly aerobic conditions, with all muscle fibres acting as normoaerobic fibres. This made these two constants conceptually independent of each other (Hill 1993; Miura et al. 2000; Poole et al. 1990; Vanhatalo and Jones 2009). This concept is criticized in the paragraph on the physiological meaning of W′.
to the power sustained in evenly aerobic conditions, with all muscle fibres acting as normoaerobic fibres. This made these two constants conceptually independent of each other (Hill 1993; Miura et al. 2000; Poole et al. 1990; Vanhatalo and Jones 2009). This concept is criticized in the paragraph on the physiological meaning of W′.
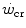 dependent, at least in part, on muscle blood flow and hence oxygen delivery. Moritani et al. (1981) associated
dependent, at least in part, on muscle blood flow and hence oxygen delivery. Moritani et al. (1981) associated 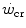 with the lactate threshold. Although it has become clear that
with the lactate threshold. Although it has become clear that 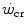 is a higher power than that corresponding to the lactate threshold, at least in non-athletic individuals (Poole et al. 1988, 1990), this may be the case in endurance athletes (Jones and Poole 2009), who are characterized by an elevated fraction of type I slow aerobic fibres in locomotory muscles as compared to the former. Subsequent studies have related W′ to overall anaerobic capacity and
is a higher power than that corresponding to the lactate threshold, at least in non-athletic individuals (Poole et al. 1988, 1990), this may be the case in endurance athletes (Jones and Poole 2009), who are characterized by an elevated fraction of type I slow aerobic fibres in locomotory muscles as compared to the former. Subsequent studies have related W′ to overall anaerobic capacity and 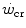 to the power sustained in evenly aerobic conditions, with all muscle fibres acting as normoaerobic fibres. This made these two constants conceptually independent of each other (Hill 1993; Miura et al. 2000; Poole et al. 1990; Vanhatalo and Jones 2009). This concept is criticized in the paragraph on the physiological meaning of W′.
to the power sustained in evenly aerobic conditions, with all muscle fibres acting as normoaerobic fibres. This made these two constants conceptually independent of each other (Hill 1993; Miura et al. 2000; Poole et al. 1990; Vanhatalo and Jones 2009). This concept is criticized in the paragraph on the physiological meaning of W′.The present definition of 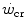 includes an oversimplification. Considering
includes an oversimplification. Considering 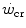 as the asymptote of hyperbolic power versus time curve implies that, for powers below the
as the asymptote of hyperbolic power versus time curve implies that, for powers below the 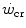 , power can be sustained for an infinite time. Obviously, this is not so. Below the
, power can be sustained for an infinite time. Obviously, this is not so. Below the 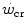 , the maximal duration is limited by the amount of substrates for aerobic exercise, which is finite. Thus, there must exist another hyperbolic power versus time relationship, whose y-axis asymptote may be the resting metabolic rate, or even the basal metabolic rate, and whose curvature is proportional to the amount of substrates for aerobic metabolism that are stored in the body, consisting of glycogen and lipids. This amount, however, is so huge that power versus time relationship at powers below the
, the maximal duration is limited by the amount of substrates for aerobic exercise, which is finite. Thus, there must exist another hyperbolic power versus time relationship, whose y-axis asymptote may be the resting metabolic rate, or even the basal metabolic rate, and whose curvature is proportional to the amount of substrates for aerobic metabolism that are stored in the body, consisting of glycogen and lipids. This amount, however, is so huge that power versus time relationship at powers below the 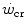 must be very flat, almost undistinguishable from a horizontal line. Saltin (1973) treated it as linear. Thus, from a practical viewpoint, the present definition of
must be very flat, almost undistinguishable from a horizontal line. Saltin (1973) treated it as linear. Thus, from a practical viewpoint, the present definition of 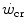 can be considered, on first approximation, acceptable, at least for exercise durations shorter than 6 h, which is approximately the best time of the 100-km run for top athletes (for an analysis of ultra-marathon running performance, see Hoffman 2010).
can be considered, on first approximation, acceptable, at least for exercise durations shorter than 6 h, which is approximately the best time of the 100-km run for top athletes (for an analysis of ultra-marathon running performance, see Hoffman 2010).
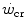 includes an oversimplification. Considering
includes an oversimplification. Considering 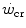 as the asymptote of hyperbolic power versus time curve implies that, for powers below the
as the asymptote of hyperbolic power versus time curve implies that, for powers below the 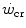 , power can be sustained for an infinite time. Obviously, this is not so. Below the
, power can be sustained for an infinite time. Obviously, this is not so. Below the 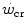 , the maximal duration is limited by the amount of substrates for aerobic exercise, which is finite. Thus, there must exist another hyperbolic power versus time relationship, whose y-axis asymptote may be the resting metabolic rate, or even the basal metabolic rate, and whose curvature is proportional to the amount of substrates for aerobic metabolism that are stored in the body, consisting of glycogen and lipids. This amount, however, is so huge that power versus time relationship at powers below the
, the maximal duration is limited by the amount of substrates for aerobic exercise, which is finite. Thus, there must exist another hyperbolic power versus time relationship, whose y-axis asymptote may be the resting metabolic rate, or even the basal metabolic rate, and whose curvature is proportional to the amount of substrates for aerobic metabolism that are stored in the body, consisting of glycogen and lipids. This amount, however, is so huge that power versus time relationship at powers below the 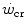 must be very flat, almost undistinguishable from a horizontal line. Saltin (1973) treated it as linear. Thus, from a practical viewpoint, the present definition of
must be very flat, almost undistinguishable from a horizontal line. Saltin (1973) treated it as linear. Thus, from a practical viewpoint, the present definition of 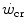 can be considered, on first approximation, acceptable, at least for exercise durations shorter than 6 h, which is approximately the best time of the 100-km run for top athletes (for an analysis of ultra-marathon running performance, see Hoffman 2010).
can be considered, on first approximation, acceptable, at least for exercise durations shorter than 6 h, which is approximately the best time of the 100-km run for top athletes (for an analysis of ultra-marathon running performance, see Hoffman 2010).The Physiological Meaning of the Energy Store Component
The energy store component W′ has received various interpretations, the meaning of which has been questioned under several respects. To date, the consensus about the concept of W′ is still weak and is undermined by the different meaning that is given to the concept of aerobic metabolism. The present discussion of W′ is carried out in the wide context of the general theory of the energetics of muscular exercise, developed by Margaria and his successors (see Chap. 1).
Mechanically speaking, there is little doubt that W′ (expressed in J) corresponds to the mechanical work that can be performed above the 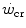 . Being a constant characterizing the power versus time relationship, its value is independent of the applied mechanical power. A corollary of the association, made by Moritani et al. (1981), between
. Being a constant characterizing the power versus time relationship, its value is independent of the applied mechanical power. A corollary of the association, made by Moritani et al. (1981), between 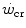 and the lactate threshold, is that
and the lactate threshold, is that 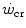 is the highest sustainable rate of aerobic metabolism, at which the maximal lactate steady state occurs (Poole et al. 1988; Pringle and Jones 2002). As a consequence, W′ was interpreted as the work that can be sustained relying on anaerobic lactic metabolism. This interpretation is affected by the notion that the lactate threshold defines the boundary between aerobic and anaerobic metabolism, which is a physiologically incorrect concept (di Prampero and Ferretti 1999), and thus, it must be rejected.
is the highest sustainable rate of aerobic metabolism, at which the maximal lactate steady state occurs (Poole et al. 1988; Pringle and Jones 2002). As a consequence, W′ was interpreted as the work that can be sustained relying on anaerobic lactic metabolism. This interpretation is affected by the notion that the lactate threshold defines the boundary between aerobic and anaerobic metabolism, which is a physiologically incorrect concept (di Prampero and Ferretti 1999), and thus, it must be rejected.
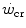 . Being a constant characterizing the power versus time relationship, its value is independent of the applied mechanical power. A corollary of the association, made by Moritani et al. (1981), between
. Being a constant characterizing the power versus time relationship, its value is independent of the applied mechanical power. A corollary of the association, made by Moritani et al. (1981), between 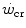 and the lactate threshold, is that
and the lactate threshold, is that 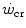 is the highest sustainable rate of aerobic metabolism, at which the maximal lactate steady state occurs (Poole et al. 1988; Pringle and Jones 2002). As a consequence, W′ was interpreted as the work that can be sustained relying on anaerobic lactic metabolism. This interpretation is affected by the notion that the lactate threshold defines the boundary between aerobic and anaerobic metabolism, which is a physiologically incorrect concept (di Prampero and Ferretti 1999), and thus, it must be rejected.
is the highest sustainable rate of aerobic metabolism, at which the maximal lactate steady state occurs (Poole et al. 1988; Pringle and Jones 2002). As a consequence, W′ was interpreted as the work that can be sustained relying on anaerobic lactic metabolism. This interpretation is affected by the notion that the lactate threshold defines the boundary between aerobic and anaerobic metabolism, which is a physiologically incorrect concept (di Prampero and Ferretti 1999), and thus, it must be rejected.Jones et al. (2010) have corrected this interpretation by adding a small aerobic contribution from myoglobin- and (venous) haemoglobin-bound oxygen stores, but this does not appear as a substantial modification of the above concept that W′ corresponds to the anaerobic capacity. Nevertheless, the same authors acknowledged that the physiological underpinnings of 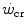 and W′ have been the subject of some controversy, for their difficulty in being assessed. They relate this to the ambiguous meaning of fatigue, which is an elegant way of admitting that the situation is confused. Based on various findings, part of which are summarized below, Jones et al. (2010) stated that “W′ may not represent a fixed “anaerobic” substrate store, but rather a mechanical work capacity that can be used while [PCr] and pH project toward a nadir value, which occurs near
and W′ have been the subject of some controversy, for their difficulty in being assessed. They relate this to the ambiguous meaning of fatigue, which is an elegant way of admitting that the situation is confused. Based on various findings, part of which are summarized below, Jones et al. (2010) stated that “W′ may not represent a fixed “anaerobic” substrate store, but rather a mechanical work capacity that can be used while [PCr] and pH project toward a nadir value, which occurs near 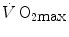 and ultimately exhaustion”. This alternate definition of the meaning of W′, however, does not bring this concept outside the domain of anaerobic capacity, although in the same paper, these authors admit that interpreting W′ as the anaerobic capacity is an oversimplification.
and ultimately exhaustion”. This alternate definition of the meaning of W′, however, does not bring this concept outside the domain of anaerobic capacity, although in the same paper, these authors admit that interpreting W′ as the anaerobic capacity is an oversimplification.
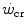 and W′ have been the subject of some controversy, for their difficulty in being assessed. They relate this to the ambiguous meaning of fatigue, which is an elegant way of admitting that the situation is confused. Based on various findings, part of which are summarized below, Jones et al. (2010) stated that “W′ may not represent a fixed “anaerobic” substrate store, but rather a mechanical work capacity that can be used while [PCr] and pH project toward a nadir value, which occurs near
and W′ have been the subject of some controversy, for their difficulty in being assessed. They relate this to the ambiguous meaning of fatigue, which is an elegant way of admitting that the situation is confused. Based on various findings, part of which are summarized below, Jones et al. (2010) stated that “W′ may not represent a fixed “anaerobic” substrate store, but rather a mechanical work capacity that can be used while [PCr] and pH project toward a nadir value, which occurs near 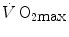 and ultimately exhaustion”. This alternate definition of the meaning of W′, however, does not bring this concept outside the domain of anaerobic capacity, although in the same paper, these authors admit that interpreting W′ as the anaerobic capacity is an oversimplification.
and ultimately exhaustion”. This alternate definition of the meaning of W′, however, does not bring this concept outside the domain of anaerobic capacity, although in the same paper, these authors admit that interpreting W′ as the anaerobic capacity is an oversimplification.If we accept the notion that 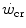 has some relation to the maximal lactate steady state, it might represent the highest power at which metabolic power is delivered in fully aerobic conditions. In this case, after the attainment of a steady state for oxygen consumption, the general equation of the energetics of muscular exercise would take the simplified form of Eq. (2.2) (see Chap. 2). Under these conditions, aerobic metabolism may be either evenly distributed, in which case all muscle fibres oxidize pyruvate via the Krebs cycle, or oddly distributed, in which case hypoaerobic type II fibres reduce part of the accumulated pyruvate into lactate: this in turn is taken up by adjacent hyperaerobic type I fibres and converted back to pyruvate, which is then fully oxidized via the Krebs cycle. The condition of uneven aerobic metabolism requires an increase in muscle and blood lactate concentrations. This increase takes place during the exercise transient (early lactate, see Chap. 3 and Cerretelli et al. 1979) and leads to stable lactate concentrations with time at a higher level than the resting one. The only difference between an even and an odd aerobic metabolism is that in the former case, the entire oxidation process from glycogen to CO2 takes place within a single muscle fibre, whereas in the latter case, the same process requires the intervention of two adjacent fibres, one working in hypoaerobic condition and accumulating lactate, and the other working in hyperaerobic condition and oxidizing lactate. Both cases are fully compatible with Eq. (2.2). An increase in lactate concentration above a given level does not define the transition from aerobic to anaerobic metabolism. Oxygen consumption still increases at powers higher than
has some relation to the maximal lactate steady state, it might represent the highest power at which metabolic power is delivered in fully aerobic conditions. In this case, after the attainment of a steady state for oxygen consumption, the general equation of the energetics of muscular exercise would take the simplified form of Eq. (2.2) (see Chap. 2). Under these conditions, aerobic metabolism may be either evenly distributed, in which case all muscle fibres oxidize pyruvate via the Krebs cycle, or oddly distributed, in which case hypoaerobic type II fibres reduce part of the accumulated pyruvate into lactate: this in turn is taken up by adjacent hyperaerobic type I fibres and converted back to pyruvate, which is then fully oxidized via the Krebs cycle. The condition of uneven aerobic metabolism requires an increase in muscle and blood lactate concentrations. This increase takes place during the exercise transient (early lactate, see Chap. 3 and Cerretelli et al. 1979) and leads to stable lactate concentrations with time at a higher level than the resting one. The only difference between an even and an odd aerobic metabolism is that in the former case, the entire oxidation process from glycogen to CO2 takes place within a single muscle fibre, whereas in the latter case, the same process requires the intervention of two adjacent fibres, one working in hypoaerobic condition and accumulating lactate, and the other working in hyperaerobic condition and oxidizing lactate. Both cases are fully compatible with Eq. (2.2). An increase in lactate concentration above a given level does not define the transition from aerobic to anaerobic metabolism. Oxygen consumption still increases at powers higher than 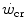 , and the maximal oxygen consumption is higher than the oxygen consumption incurring at the
, and the maximal oxygen consumption is higher than the oxygen consumption incurring at the 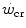 .
.
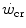 has some relation to the maximal lactate steady state, it might represent the highest power at which metabolic power is delivered in fully aerobic conditions. In this case, after the attainment of a steady state for oxygen consumption, the general equation of the energetics of muscular exercise would take the simplified form of Eq. (2.2) (see Chap. 2). Under these conditions, aerobic metabolism may be either evenly distributed, in which case all muscle fibres oxidize pyruvate via the Krebs cycle, or oddly distributed, in which case hypoaerobic type II fibres reduce part of the accumulated pyruvate into lactate: this in turn is taken up by adjacent hyperaerobic type I fibres and converted back to pyruvate, which is then fully oxidized via the Krebs cycle. The condition of uneven aerobic metabolism requires an increase in muscle and blood lactate concentrations. This increase takes place during the exercise transient (early lactate, see Chap. 3 and Cerretelli et al. 1979) and leads to stable lactate concentrations with time at a higher level than the resting one. The only difference between an even and an odd aerobic metabolism is that in the former case, the entire oxidation process from glycogen to CO2 takes place within a single muscle fibre, whereas in the latter case, the same process requires the intervention of two adjacent fibres, one working in hypoaerobic condition and accumulating lactate, and the other working in hyperaerobic condition and oxidizing lactate. Both cases are fully compatible with Eq. (2.2). An increase in lactate concentration above a given level does not define the transition from aerobic to anaerobic metabolism. Oxygen consumption still increases at powers higher than
has some relation to the maximal lactate steady state, it might represent the highest power at which metabolic power is delivered in fully aerobic conditions. In this case, after the attainment of a steady state for oxygen consumption, the general equation of the energetics of muscular exercise would take the simplified form of Eq. (2.2) (see Chap. 2). Under these conditions, aerobic metabolism may be either evenly distributed, in which case all muscle fibres oxidize pyruvate via the Krebs cycle, or oddly distributed, in which case hypoaerobic type II fibres reduce part of the accumulated pyruvate into lactate: this in turn is taken up by adjacent hyperaerobic type I fibres and converted back to pyruvate, which is then fully oxidized via the Krebs cycle. The condition of uneven aerobic metabolism requires an increase in muscle and blood lactate concentrations. This increase takes place during the exercise transient (early lactate, see Chap. 3 and Cerretelli et al. 1979) and leads to stable lactate concentrations with time at a higher level than the resting one. The only difference between an even and an odd aerobic metabolism is that in the former case, the entire oxidation process from glycogen to CO2 takes place within a single muscle fibre, whereas in the latter case, the same process requires the intervention of two adjacent fibres, one working in hypoaerobic condition and accumulating lactate, and the other working in hyperaerobic condition and oxidizing lactate. Both cases are fully compatible with Eq. (2.2). An increase in lactate concentration above a given level does not define the transition from aerobic to anaerobic metabolism. Oxygen consumption still increases at powers higher than 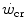 , and the maximal oxygen consumption is higher than the oxygen consumption incurring at the
, and the maximal oxygen consumption is higher than the oxygen consumption incurring at the 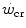 .
.The above reasoning includes the demonstration that W′ does not represent anaerobic capacity, even with the addition of a small aerobic component from oxygen stores. The energy balance in the range of powers comprised between 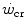 and the maximal aerobic power (
and the maximal aerobic power (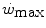 ), which defines the intense exercise domain, consists of a mixture of energy derived from aerobic and from anaerobic sources. Oxygen consumption does still increase, because it has not achieved the uppermost limit that mitochondrial oxidative capacity is able to attain and/or because it can be sustained by a further increase in systemic oxygen delivery. In other terms, neither the peripheral resistance nor the cardiovascular resistance to oxygen flow has yet attained their minimal value at the
), which defines the intense exercise domain, consists of a mixture of energy derived from aerobic and from anaerobic sources. Oxygen consumption does still increase, because it has not achieved the uppermost limit that mitochondrial oxidative capacity is able to attain and/or because it can be sustained by a further increase in systemic oxygen delivery. In other terms, neither the peripheral resistance nor the cardiovascular resistance to oxygen flow has yet attained their minimal value at the 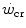 .
.
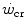 and the maximal aerobic power (
and the maximal aerobic power (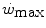 ), which defines the intense exercise domain, consists of a mixture of energy derived from aerobic and from anaerobic sources. Oxygen consumption does still increase, because it has not achieved the uppermost limit that mitochondrial oxidative capacity is able to attain and/or because it can be sustained by a further increase in systemic oxygen delivery. In other terms, neither the peripheral resistance nor the cardiovascular resistance to oxygen flow has yet attained their minimal value at the
), which defines the intense exercise domain, consists of a mixture of energy derived from aerobic and from anaerobic sources. Oxygen consumption does still increase, because it has not achieved the uppermost limit that mitochondrial oxidative capacity is able to attain and/or because it can be sustained by a further increase in systemic oxygen delivery. In other terms, neither the peripheral resistance nor the cardiovascular resistance to oxygen flow has yet attained their minimal value at the 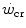 .
.At the same time, the number of muscle fibres operating in hypoaerobic condition goes up as the mechanical power increases, as does their rate of lactate production, until a power is attained at which the lactate produced by hypoaerobic power exceeds the capacity of hyperaerobic fibres to remove it. Also these fibres in fact increase the rate at which they oxidize glycogen, and thus have fewer margins to face a higher rate of lactate production by hypoaerobic fibres. Once this condition has been attained, lactate concentration keeps increasing with time at a rate which is higher the higher the mechanical power, and anaerobic lactic power (see Chap. 6) becomes positive.
This line of reasoning applies only to the fraction of mechanical power above the 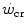 , which even at
, which even at 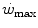 represents a relatively small amount with respect to the total applied mechanical power. Within the power range between
represents a relatively small amount with respect to the total applied mechanical power. Within the power range between 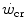 and
and 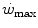 , we may also account for the “slow component” of muscle phosphocreatine decrease (Rossiter et al. 2002). If we assume that this is associated with the activation of anaerobic alactic metabolism, we can state that during intense exercise, above
, we may also account for the “slow component” of muscle phosphocreatine decrease (Rossiter et al. 2002). If we assume that this is associated with the activation of anaerobic alactic metabolism, we can state that during intense exercise, above 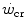 but below
but below 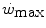 , all the three main energy metabolisms are simultaneously active also at exercise times longer than the 4–5 min that classically define the duration of the exercise transient. Note that this is the same power range in which the slow component of the oxygen uptake kinetics (Chap. 3) becomes visible. If we finally consider that, at the net of the oxygen deficit, all the power between rest and
, all the three main energy metabolisms are simultaneously active also at exercise times longer than the 4–5 min that classically define the duration of the exercise transient. Note that this is the same power range in which the slow component of the oxygen uptake kinetics (Chap. 3) becomes visible. If we finally consider that, at the net of the oxygen deficit, all the power between rest and 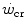 is sustained by aerobic metabolism, oxygen consumption represents anyway and by far the largest contributor to the overall metabolic rate also at powers comprised between
is sustained by aerobic metabolism, oxygen consumption represents anyway and by far the largest contributor to the overall metabolic rate also at powers comprised between 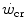 and
and 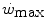 .
.
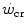 , which even at
, which even at 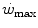 represents a relatively small amount with respect to the total applied mechanical power. Within the power range between
represents a relatively small amount with respect to the total applied mechanical power. Within the power range between 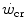 and
and 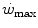 , we may also account for the “slow component” of muscle phosphocreatine decrease (Rossiter et al. 2002). If we assume that this is associated with the activation of anaerobic alactic metabolism, we can state that during intense exercise, above
, we may also account for the “slow component” of muscle phosphocreatine decrease (Rossiter et al. 2002). If we assume that this is associated with the activation of anaerobic alactic metabolism, we can state that during intense exercise, above 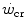 but below
but below 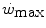 , all the three main energy metabolisms are simultaneously active also at exercise times longer than the 4–5 min that classically define the duration of the exercise transient. Note that this is the same power range in which the slow component of the oxygen uptake kinetics (Chap. 3) becomes visible. If we finally consider that, at the net of the oxygen deficit, all the power between rest and
, all the three main energy metabolisms are simultaneously active also at exercise times longer than the 4–5 min that classically define the duration of the exercise transient. Note that this is the same power range in which the slow component of the oxygen uptake kinetics (Chap. 3) becomes visible. If we finally consider that, at the net of the oxygen deficit, all the power between rest and 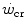 is sustained by aerobic metabolism, oxygen consumption represents anyway and by far the largest contributor to the overall metabolic rate also at powers comprised between
is sustained by aerobic metabolism, oxygen consumption represents anyway and by far the largest contributor to the overall metabolic rate also at powers comprised between 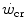 and
and 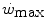 .
.Descriptive Physiology of Critical Power and Energy Store Component
For reasons that are outlined below, pertaining to the strict relations between 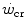 and
and 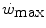 , all chronic adaptive phenomena and all acute manoeuvres that act on
, all chronic adaptive phenomena and all acute manoeuvres that act on 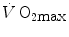 , and thus on
, and thus on 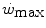 , act also on
, act also on 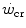 . Not all conditions, however, have been investigated in terms of effects on
. Not all conditions, however, have been investigated in terms of effects on 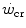 . In any case, and coherently with the principles pointed out here above, it has been demonstrated that both continuous (Heubert et al. 2003; Jenkins and Quigley 1992) and high-intensity interval training (Gaesser and Wilson 1988; Jenkins and Quigley 1993; Kendall et al. 2009; Poole et al. 1990; Vanhatalo et al. 2008) increase
. In any case, and coherently with the principles pointed out here above, it has been demonstrated that both continuous (Heubert et al. 2003; Jenkins and Quigley 1992) and high-intensity interval training (Gaesser and Wilson 1988; Jenkins and Quigley 1993; Kendall et al. 2009; Poole et al. 1990; Vanhatalo et al. 2008) increase 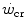 . Moreover, strength training was shown to increase the time to exhaustion during high-intensity exercise by an effect on W′ without changes of
. Moreover, strength training was shown to increase the time to exhaustion during high-intensity exercise by an effect on W′ without changes of 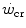 (Sawyer et al. 2014). It seems logical to expect a decrease in
(Sawyer et al. 2014). It seems logical to expect a decrease in 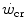 after prolonged bed rest, especially during upright exercise, but I am unaware of any study specifically addressing this issue. Conversely, there is some evidence that
after prolonged bed rest, especially during upright exercise, but I am unaware of any study specifically addressing this issue. Conversely, there is some evidence that 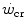 goes down in hypoxia (Dekerle et al. 2012; Moritani et al. 1981; Parker-Simpson et al. 2014; Valli et al. 2011). Possibly for its effects on muscle blood flow, and thus on the rate of lactate accumulation, prior high-intensity exercise displaces
goes down in hypoxia (Dekerle et al. 2012; Moritani et al. 1981; Parker-Simpson et al. 2014; Valli et al. 2011). Possibly for its effects on muscle blood flow, and thus on the rate of lactate accumulation, prior high-intensity exercise displaces 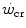 closer to
closer to 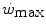 and reduces W′ (Ferguson et al. 2007, 2010; Miura et al. 2009; Vanhatalo and Jones 2009).
and reduces W′ (Ferguson et al. 2007, 2010; Miura et al. 2009; Vanhatalo and Jones 2009).
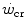 and
and 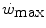 , all chronic adaptive phenomena and all acute manoeuvres that act on
, all chronic adaptive phenomena and all acute manoeuvres that act on 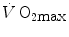 , and thus on
, and thus on 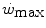 , act also on
, act also on 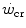 . Not all conditions, however, have been investigated in terms of effects on
. Not all conditions, however, have been investigated in terms of effects on 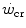 . In any case, and coherently with the principles pointed out here above, it has been demonstrated that both continuous (Heubert et al. 2003; Jenkins and Quigley 1992) and high-intensity interval training (Gaesser and Wilson 1988; Jenkins and Quigley 1993; Kendall et al. 2009; Poole et al. 1990; Vanhatalo et al. 2008) increase
. In any case, and coherently with the principles pointed out here above, it has been demonstrated that both continuous (Heubert et al. 2003; Jenkins and Quigley 1992) and high-intensity interval training (Gaesser and Wilson 1988; Jenkins and Quigley 1993; Kendall et al. 2009; Poole et al. 1990; Vanhatalo et al. 2008) increase 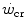 . Moreover, strength training was shown to increase the time to exhaustion during high-intensity exercise by an effect on W′ without changes of
. Moreover, strength training was shown to increase the time to exhaustion during high-intensity exercise by an effect on W′ without changes of 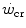 (Sawyer et al. 2014). It seems logical to expect a decrease in
(Sawyer et al. 2014). It seems logical to expect a decrease in 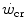 after prolonged bed rest, especially during upright exercise, but I am unaware of any study specifically addressing this issue. Conversely, there is some evidence that
after prolonged bed rest, especially during upright exercise, but I am unaware of any study specifically addressing this issue. Conversely, there is some evidence that 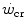 goes down in hypoxia (Dekerle et al. 2012; Moritani et al. 1981; Parker-Simpson et al. 2014; Valli et al. 2011). Possibly for its effects on muscle blood flow, and thus on the rate of lactate accumulation, prior high-intensity exercise displaces
goes down in hypoxia (Dekerle et al. 2012; Moritani et al. 1981; Parker-Simpson et al. 2014; Valli et al. 2011). Possibly for its effects on muscle blood flow, and thus on the rate of lactate accumulation, prior high-intensity exercise displaces 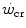 closer to
closer to 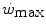 and reduces W′ (Ferguson et al. 2007, 2010; Miura et al. 2009; Vanhatalo and Jones 2009).
and reduces W′ (Ferguson et al. 2007, 2010; Miura et al. 2009; Vanhatalo and Jones 2009).Interesting is the case of hyperoxia. If the degree of hyperoxia is sufficiently strong, so that the concentration of free oxygen in blood becomes significant, hyperoxia increases 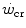 , thus reducing the rate at which lactate concentration goes up and muscle phosphocreatine goes down at a given power. Since hyperoxia does not increase
, thus reducing the rate at which lactate concentration goes up and muscle phosphocreatine goes down at a given power. Since hyperoxia does not increase 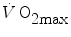 , and thus
, and thus 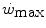 , this reduces the difference between
, this reduces the difference between 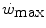 and
and 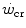 , so that the size of the energy store component W′ inevitably decreases, as demonstrated by Vanhatalo et al. (2010). More generally speaking, I would tend to state that whenever the difference between
, so that the size of the energy store component W′ inevitably decreases, as demonstrated by Vanhatalo et al. (2010). More generally speaking, I would tend to state that whenever the difference between 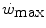 and
and 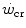 is reduced—implying an increase of the
is reduced—implying an increase of the 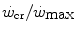 ratio—the size of W′ decreases; conversely, whenever the difference between
ratio—the size of W′ decreases; conversely, whenever the difference between 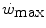 and
and 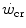 is enhanced, the size of W′ increases. The
is enhanced, the size of W′ increases. The 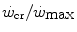 ratio is increased also when there is an identical absolute increase in
ratio is increased also when there is an identical absolute increase in 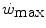 and
and 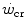 . This occurs for instance during exercise training (Heubert et al. 2003; Jenkins and Quigley 1992): also in this condition, the increase in
. This occurs for instance during exercise training (Heubert et al. 2003; Jenkins and Quigley 1992): also in this condition, the increase in 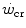 is accompanied by a decrease in W′ (Vanhatalo et al. 2008).
is accompanied by a decrease in W′ (Vanhatalo et al. 2008).
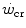 , thus reducing the rate at which lactate concentration goes up and muscle phosphocreatine goes down at a given power. Since hyperoxia does not increase
, thus reducing the rate at which lactate concentration goes up and muscle phosphocreatine goes down at a given power. Since hyperoxia does not increase 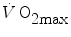 , and thus
, and thus 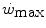 , this reduces the difference between
, this reduces the difference between 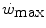 and
and 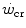 , so that the size of the energy store component W′ inevitably decreases, as demonstrated by Vanhatalo et al. (2010). More generally speaking, I would tend to state that whenever the difference between
, so that the size of the energy store component W′ inevitably decreases, as demonstrated by Vanhatalo et al. (2010). More generally speaking, I would tend to state that whenever the difference between 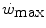 and
and 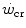 is reduced—implying an increase of the
is reduced—implying an increase of the 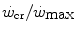 ratio—the size of W′ decreases; conversely, whenever the difference between
ratio—the size of W′ decreases; conversely, whenever the difference between 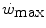 and
and 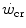 is enhanced, the size of W′ increases. The
is enhanced, the size of W′ increases. The 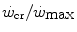 ratio is increased also when there is an identical absolute increase in
ratio is increased also when there is an identical absolute increase in 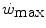 and
and 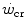 . This occurs for instance during exercise training (Heubert et al. 2003; Jenkins and Quigley 1992): also in this condition, the increase in
. This occurs for instance during exercise training (Heubert et al. 2003; Jenkins and Quigley 1992): also in this condition, the increase in 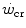 is accompanied by a decrease in W′ (Vanhatalo et al. 2008).
is accompanied by a decrease in W′ (Vanhatalo et al. 2008).Interventions specifically acting on substrate stores can be predicted to have an effect on W′, which is positive if substrate stores are enlarged, negative in the opposite case. Coherently with this prediction, glycogen depletion reduces W′ (Miura et al. 2000), whereas creatine supplementation increases it (Kendall et al. 2009; Smith et al. 1998).
All these results are coherent with the energetic meaning of 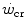 and W′ outlined previously. They thus provide strong experimental support to the concepts that (i)
and W′ outlined previously. They thus provide strong experimental support to the concepts that (i) 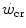 represents the upper limit of unevenly distributed aerobic metabolism as summarized by Eq. (2.2), and (ii) the energetics of W′ consists of the simultaneous intervention of aerobic, anaerobic lactic and eventually also anaerobic alactic metabolism.
represents the upper limit of unevenly distributed aerobic metabolism as summarized by Eq. (2.2), and (ii) the energetics of W′ consists of the simultaneous intervention of aerobic, anaerobic lactic and eventually also anaerobic alactic metabolism.
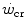 and W′ outlined previously. They thus provide strong experimental support to the concepts that (i)
and W′ outlined previously. They thus provide strong experimental support to the concepts that (i) 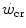 represents the upper limit of unevenly distributed aerobic metabolism as summarized by Eq. (2.2), and (ii) the energetics of W′ consists of the simultaneous intervention of aerobic, anaerobic lactic and eventually also anaerobic alactic metabolism.
represents the upper limit of unevenly distributed aerobic metabolism as summarized by Eq. (2.2), and (ii) the energetics of W′ consists of the simultaneous intervention of aerobic, anaerobic lactic and eventually also anaerobic alactic metabolism.Energetic Consequences of the Hyperbolic Critical Power Model
The hyperbolic model of 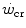 originally conceived by Monod and Scherrer (1965) and represented in Fig. 5.1 can be algebraically represented in the following form:
originally conceived by Monod and Scherrer (1965) and represented in Fig. 5.1 can be algebraically represented in the following form:
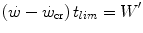
where t lim is the maximal time over which a given 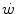 above the
above the 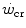 can be sustained. Equation (5.1) tells that t lim is inversely proportional and W′ is directly proportional to the
can be sustained. Equation (5.1) tells that t lim is inversely proportional and W′ is directly proportional to the 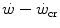 difference. Equation (5.1) therefore provides a solid theoretical explanation of the experimental results reported in the preceding paragraph and allows precise predictions of how the power versus time relationship evolves when chronic adaptive changes or acute manoeuvres alter W′ and/or
difference. Equation (5.1) therefore provides a solid theoretical explanation of the experimental results reported in the preceding paragraph and allows precise predictions of how the power versus time relationship evolves when chronic adaptive changes or acute manoeuvres alter W′ and/or 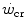 .
.
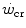 originally conceived by Monod and Scherrer (1965) and represented in Fig. 5.1 can be algebraically represented in the following form:
originally conceived by Monod and Scherrer (1965) and represented in Fig. 5.1 can be algebraically represented in the following form: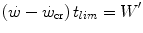
(5.1)
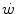 above the
above the 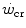 can be sustained. Equation (5.1) tells that t lim is inversely proportional and W′ is directly proportional to the
can be sustained. Equation (5.1) tells that t lim is inversely proportional and W′ is directly proportional to the 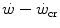 difference. Equation (5.1) therefore provides a solid theoretical explanation of the experimental results reported in the preceding paragraph and allows precise predictions of how the power versus time relationship evolves when chronic adaptive changes or acute manoeuvres alter W′ and/or
difference. Equation (5.1) therefore provides a solid theoretical explanation of the experimental results reported in the preceding paragraph and allows precise predictions of how the power versus time relationship evolves when chronic adaptive changes or acute manoeuvres alter W′ and/or 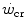 .
.The total amount of mechanical work (W) carried out during a square wave exercise lasting a time equal to t lim is given by:
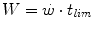
whence, after combining Eqs. (5.1) and (5.2) and rearranging, we obtain:
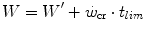
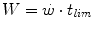
(5.2)
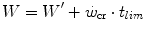
(5.3)
Equation (5.3) can be expressed in terms of metabolic energy as follows:
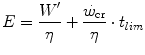
where η is the mechanical efficiency of exercise. Since the lactate concentration at the steady state of an exercise carried out at 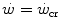 does not vary with time, the ratio
does not vary with time, the ratio 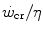 corresponds to the net (measured value minus resting value) steady-state oxygen consumption at the
corresponds to the net (measured value minus resting value) steady-state oxygen consumption at the 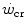 , which I propose to call the critical oxygen consumption (
, which I propose to call the critical oxygen consumption (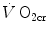 ), and Eq. (5.4) can be rewritten as follows:
), and Eq. (5.4) can be rewritten as follows:
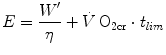
where the ratio 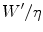 , according to the general equation of the energetics of muscular exercise, is equal to:
, according to the general equation of the energetics of muscular exercise, is equal to:
![$$ \frac{{W^{\prime } }}{\eta } = \left[ {\left( {\dot{V}\,{\text{O}}_{2} - \dot{V}\,{\text{O}}_{{2{\text{cr}}}} } \right) + \beta\dot{L}a} \right]t_{lim} $$](/wp-content/uploads/2016/09/A322139_1_En_5_Chapter_Equ6.gif)
where 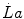 is the rate at which lactate concentration in blood increases (slope of a lactate versus time line) after the first 5 min of exercise, and β is a proportionality constant indicating the amount of energy corresponding to a mole of lactate accumulated in blood (energy equivalent of blood lactate accumulation, see Chap. 6). Combining Eqs. (5.5) and (5.6) yields:
is the rate at which lactate concentration in blood increases (slope of a lactate versus time line) after the first 5 min of exercise, and β is a proportionality constant indicating the amount of energy corresponding to a mole of lactate accumulated in blood (energy equivalent of blood lactate accumulation, see Chap. 6). Combining Eqs. (5.5) and (5.6) yields:
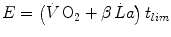
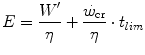
(5.4)
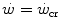 does not vary with time, the ratio
does not vary with time, the ratio 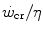 corresponds to the net (measured value minus resting value) steady-state oxygen consumption at the
corresponds to the net (measured value minus resting value) steady-state oxygen consumption at the 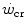 , which I propose to call the critical oxygen consumption (
, which I propose to call the critical oxygen consumption (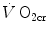 ), and Eq. (5.4) can be rewritten as follows:
), and Eq. (5.4) can be rewritten as follows: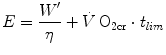
(5.5)
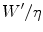 , according to the general equation of the energetics of muscular exercise, is equal to:
, according to the general equation of the energetics of muscular exercise, is equal to:![$$ \frac{{W^{\prime } }}{\eta } = \left[ {\left( {\dot{V}\,{\text{O}}_{2} - \dot{V}\,{\text{O}}_{{2{\text{cr}}}} } \right) + \beta\dot{L}a} \right]t_{lim} $$](/wp-content/uploads/2016/09/A322139_1_En_5_Chapter_Equ6.gif)
(5.6)
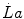 is the rate at which lactate concentration in blood increases (slope of a lactate versus time line) after the first 5 min of exercise, and β is a proportionality constant indicating the amount of energy corresponding to a mole of lactate accumulated in blood (energy equivalent of blood lactate accumulation, see Chap. 6). Combining Eqs. (5.5) and (5.6) yields:
is the rate at which lactate concentration in blood increases (slope of a lactate versus time line) after the first 5 min of exercise, and β is a proportionality constant indicating the amount of energy corresponding to a mole of lactate accumulated in blood (energy equivalent of blood lactate accumulation, see Chap. 6). Combining Eqs. (5.5) and (5.6) yields: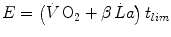
(5.7)
In Eq. (5.7), 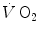 is the net oxygen consumption, to be expressed in watts when energy is expressed in joules (note that 1 L of oxygen STPD provides about 20.9 kJ of energy).
is the net oxygen consumption, to be expressed in watts when energy is expressed in joules (note that 1 L of oxygen STPD provides about 20.9 kJ of energy). 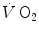 corresponds to the asymptote of the primary component of the oxygen consumption kinetics (steady state of phase II) and includes the energy derived from anaerobic sources during contraction of the oxygen deficit (O2def), which is given by.
corresponds to the asymptote of the primary component of the oxygen consumption kinetics (steady state of phase II) and includes the energy derived from anaerobic sources during contraction of the oxygen deficit (O2def), which is given by.
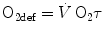
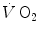 is the net oxygen consumption, to be expressed in watts when energy is expressed in joules (note that 1 L of oxygen STPD provides about 20.9 kJ of energy).
is the net oxygen consumption, to be expressed in watts when energy is expressed in joules (note that 1 L of oxygen STPD provides about 20.9 kJ of energy). 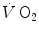 corresponds to the asymptote of the primary component of the oxygen consumption kinetics (steady state of phase II) and includes the energy derived from anaerobic sources during contraction of the oxygen deficit (O2def), which is given by.
corresponds to the asymptote of the primary component of the oxygen consumption kinetics (steady state of phase II) and includes the energy derived from anaerobic sources during contraction of the oxygen deficit (O2def), which is given by.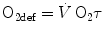
(5.8)
Because of Eq. (3.4), Eq. (5.8) can be rewritten as follows:
![$$ {\text{O}}_{{ 2 {\text{def}}}} = \dot{V}\,{\text{O}}_{2} \cdot (\lambda \cdot \left[ {\text{La}} \right]_{\text{e}} + \tau_{0} ) $$](/wp-content/uploads/2016/09/A322139_1_En_5_Chapter_Equ9.gif)
where the lactate concentration [La]e represents early lactate, λ is the constant indicating how much 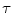 increases per unit increase of lactate in blood during the exercise transient (di Prampero and Ferretti 1999), and
increases per unit increase of lactate in blood during the exercise transient (di Prampero and Ferretti 1999), and 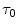 is the time constant of the obligatory component of the oxygen deficit, i.e. the time constant that would incur in the absence of early lactate accumulation. The
is the time constant of the obligatory component of the oxygen deficit, i.e. the time constant that would incur in the absence of early lactate accumulation. The 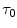 values range between 23 and 30 s (see Chap. 3), which corresponds well to the time constant of muscle phosphocreatine depletion upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2008, 2013; Rossiter et al. 1999, 2002). Therefore, during exercise at any power
values range between 23 and 30 s (see Chap. 3), which corresponds well to the time constant of muscle phosphocreatine depletion upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2008, 2013; Rossiter et al. 1999, 2002). Therefore, during exercise at any power 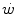 higher than
higher than 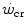 , the amount of energy derived from the anaerobic lactic component (E La ) of the metabolic energy expenditure is equal to:
, the amount of energy derived from the anaerobic lactic component (E La ) of the metabolic energy expenditure is equal to:
![$$ {\text{O}}_{{ 2 {\text{def}}}} = \dot{V}\,{\text{O}}_{2} \cdot (\lambda \cdot \left[ {\text{La}} \right]_{\text{e}} + \tau_{0} ) $$](/wp-content/uploads/2016/09/A322139_1_En_5_Chapter_Equ9.gif)
(5.9)
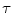 increases per unit increase of lactate in blood during the exercise transient (di Prampero and Ferretti 1999), and
increases per unit increase of lactate in blood during the exercise transient (di Prampero and Ferretti 1999), and 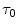 is the time constant of the obligatory component of the oxygen deficit, i.e. the time constant that would incur in the absence of early lactate accumulation. The
is the time constant of the obligatory component of the oxygen deficit, i.e. the time constant that would incur in the absence of early lactate accumulation. The 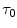 values range between 23 and 30 s (see Chap. 3), which corresponds well to the time constant of muscle phosphocreatine depletion upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2008, 2013; Rossiter et al. 1999, 2002). Therefore, during exercise at any power
values range between 23 and 30 s (see Chap. 3), which corresponds well to the time constant of muscle phosphocreatine depletion upon exercise onset (Binzoni et al. 1992; di Prampero et al. 2003; Francescato et al. 2008, 2013; Rossiter et al. 1999, 2002). Therefore, during exercise at any power 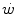 higher than
higher than 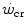 , the amount of energy derived from the anaerobic lactic component (E La ) of the metabolic energy expenditure is equal to:
, the amount of energy derived from the anaerobic lactic component (E La ) of the metabolic energy expenditure is equal to: