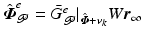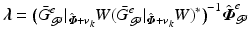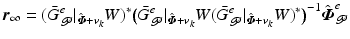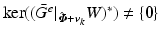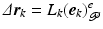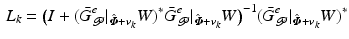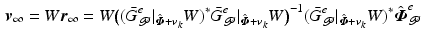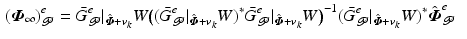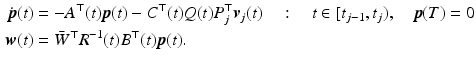to track reference trajectory 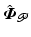 , where operator
, where operator 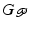 is defined by (4.1). This objective assumes that a trajectory
is defined by (4.1). This objective assumes that a trajectory ![$$\hat{\varvec{\varPhi }}_{\mathscr {P}}(t), \; t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq4.gif) is available. In the rehabilitation domain this is appropriate if the task is defined and explicitly presented to the patient as it was in Chap. 5. However, this is not possible when training more natural, everyday activities such as eating, washing or manipulating objects. To address this, the problem definition is now extended to encompass fully functional tasks.
is available. In the rehabilitation domain this is appropriate if the task is defined and explicitly presented to the patient as it was in Chap. 5. However, this is not possible when training more natural, everyday activities such as eating, washing or manipulating objects. To address this, the problem definition is now extended to encompass fully functional tasks.
6.1 Extended Task Representation
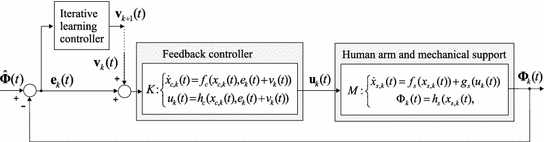
Fig. 6.1
Combined feedback and ILC control structure
To expand the task definition to capture the needs of human motor control, we define 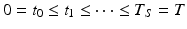 distinct points in [0, T] which are deemed important to the task completion. These break the task down into S intervals in which one or more joints may be required to perform a synchronized movement. For example, time interval
distinct points in [0, T] which are deemed important to the task completion. These break the task down into S intervals in which one or more joints may be required to perform a synchronized movement. For example, time interval ![$$[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq6.gif) may correspond to the hand palm pushing a drawer along its runners, or the fingers holding a cup during a pouring movement. If
may correspond to the hand palm pushing a drawer along its runners, or the fingers holding a cup during a pouring movement. If 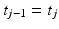 is specified then the interval is an isolated time point, and may for example represent the time where the index finger makes contact with a light switch.
is specified then the interval is an isolated time point, and may for example represent the time where the index finger makes contact with a light switch.
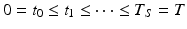 distinct points in [0, T] which are deemed important to the task completion. These break the task down into S intervals in which one or more joints may be required to perform a synchronized movement. For example, time interval
distinct points in [0, T] which are deemed important to the task completion. These break the task down into S intervals in which one or more joints may be required to perform a synchronized movement. For example, time interval ![$$[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq6.gif) may correspond to the hand palm pushing a drawer along its runners, or the fingers holding a cup during a pouring movement. If
may correspond to the hand palm pushing a drawer along its runners, or the fingers holding a cup during a pouring movement. If 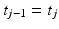 is specified then the interval is an isolated time point, and may for example represent the time where the index finger makes contact with a light switch.
is specified then the interval is an isolated time point, and may for example represent the time where the index finger makes contact with a light switch.Given joint angle signal 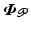 defined over [0, T], we extract the single or linear combination of joints involved in any coordinated action by using the projection
defined over [0, T], we extract the single or linear combination of joints involved in any coordinated action by using the projection
![$$\begin{aligned} P&: \mathscr {L}_2^{n_p} [0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}] : \varvec{\varPhi }_{\mathscr {P}} \mapsto \left[ \begin{array}{c} (P \varvec{\varPhi }_{\mathscr {P}})_1 \\ \vdots \\ (P \varvec{\varPhi }_{\mathscr {P}})_S \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ1.gif)
with each component, ![$$(P \varvec{\varPhi }_{\mathscr {P}})_j: \mathscr {L}_2^{n_p}[0,T] \rightarrow \mathscr {L}_2^{p_j}[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq9.gif) , defined by
, defined by
![$$\begin{aligned} ((P \varvec{\varPhi }_{\mathscr {P}})_j )(t) = P_j \varvec{\varPhi }_{\mathscr {P}}(t), \quad \quad t \in [t_{j-1}, t_j], \quad j = 1, 2, \ldots , S, \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ2.gif)
where 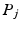 is a
is a 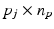 matrix of full row rank specifying the joint angles involved in the gesture or movement stipulated over time interval
matrix of full row rank specifying the joint angles involved in the gesture or movement stipulated over time interval ![$$[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq12.gif) .
.
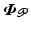 defined over [0, T], we extract the single or linear combination of joints involved in any coordinated action by using the projection
defined over [0, T], we extract the single or linear combination of joints involved in any coordinated action by using the projection![$$\begin{aligned} P&: \mathscr {L}_2^{n_p} [0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}] : \varvec{\varPhi }_{\mathscr {P}} \mapsto \left[ \begin{array}{c} (P \varvec{\varPhi }_{\mathscr {P}})_1 \\ \vdots \\ (P \varvec{\varPhi }_{\mathscr {P}})_S \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ1.gif)
(6.1)
![$$(P \varvec{\varPhi }_{\mathscr {P}})_j: \mathscr {L}_2^{n_p}[0,T] \rightarrow \mathscr {L}_2^{p_j}[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq9.gif) , defined by
, defined by![$$\begin{aligned} ((P \varvec{\varPhi }_{\mathscr {P}})_j )(t) = P_j \varvec{\varPhi }_{\mathscr {P}}(t), \quad \quad t \in [t_{j-1}, t_j], \quad j = 1, 2, \ldots , S, \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ2.gif)
(6.2)
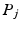 is a
is a 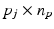 matrix of full row rank specifying the joint angles involved in the gesture or movement stipulated over time interval
matrix of full row rank specifying the joint angles involved in the gesture or movement stipulated over time interval ![$$[t_{j-1}, t_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq12.gif) .
.For ease of notation, the projected output 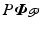 is termed the “extended output” and denoted by
is termed the “extended output” and denoted by ![$$\varvec{\varPhi }_{\mathscr {P}}^e \in \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq14.gif) . We can also incorporate the projection into the system operator to yield the extended system operator
. We can also incorporate the projection into the system operator to yield the extended system operator ![$$G_{\mathscr {P}}^e : \mathscr {L}_2^{p} [0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq15.gif) defined by
defined by
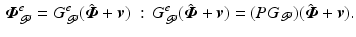
Using this extended task representation allows us to replace the ILC tracking problem (4.3) by the more general form
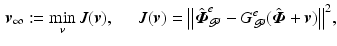
where the extended reference trajectory and extended error are respectively
![$$\begin{aligned} \hat{\varvec{\varPhi }}_{\mathscr {P}}^e = \left[ \begin{array}{c} \hat{\varvec{\varPhi }}^{p_1}_{\mathscr {P}} \\ \vdots \\ \hat{\varvec{\varPhi }}^{p_S}_{\mathscr {P}} \end{array} \right] , \quad \varvec{e}_{\mathscr {P}}^e = \left[ \begin{array}{c} \hat{\varvec{\varPhi }}^{p_1}_{\mathscr {P}} - (P G_{\mathscr {P}})_1 (\hat{\varvec{\varPhi }} + \varvec{v}) \\ \vdots \\ \hat{\varvec{\varPhi }}^{p_S}_{\mathscr {P}} - (P G_{\mathscr {P}})_S (\hat{\varvec{\varPhi }} + \varvec{v}) \end{array} \right] = \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - G_{\mathscr {P}}^e (\hat{\varvec{\varPhi }} + \varvec{v}). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ5.gif)
Here 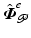 contains the reference trajectories/points that must be followed at time points
contains the reference trajectories/points that must be followed at time points 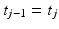 or over intervals
or over intervals ![$$[{t}_{j-1}, {t}_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq18.gif) . Note that the extended reference can be represented as the projection of a “virtual reference”,
. Note that the extended reference can be represented as the projection of a “virtual reference”, 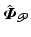 , denoted by
, denoted by 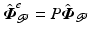 , however
, however 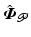 is not required in the control strategy. If the designer chooses
is not required in the control strategy. If the designer chooses 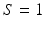 ,
, 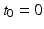 ,
, 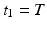 , and
, and 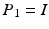 then (6.4) collapses to the standard form (4.3).
then (6.4) collapses to the standard form (4.3).
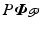 is termed the “extended output” and denoted by
is termed the “extended output” and denoted by ![$$\varvec{\varPhi }_{\mathscr {P}}^e \in \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq14.gif) . We can also incorporate the projection into the system operator to yield the extended system operator
. We can also incorporate the projection into the system operator to yield the extended system operator ![$$G_{\mathscr {P}}^e : \mathscr {L}_2^{p} [0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq15.gif) defined by
defined by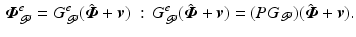
(6.3)
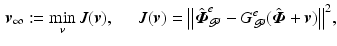
(6.4)
![$$\begin{aligned} \hat{\varvec{\varPhi }}_{\mathscr {P}}^e = \left[ \begin{array}{c} \hat{\varvec{\varPhi }}^{p_1}_{\mathscr {P}} \\ \vdots \\ \hat{\varvec{\varPhi }}^{p_S}_{\mathscr {P}} \end{array} \right] , \quad \varvec{e}_{\mathscr {P}}^e = \left[ \begin{array}{c} \hat{\varvec{\varPhi }}^{p_1}_{\mathscr {P}} - (P G_{\mathscr {P}})_1 (\hat{\varvec{\varPhi }} + \varvec{v}) \\ \vdots \\ \hat{\varvec{\varPhi }}^{p_S}_{\mathscr {P}} - (P G_{\mathscr {P}})_S (\hat{\varvec{\varPhi }} + \varvec{v}) \end{array} \right] = \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - G_{\mathscr {P}}^e (\hat{\varvec{\varPhi }} + \varvec{v}). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ5.gif)
(6.5)
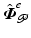 contains the reference trajectories/points that must be followed at time points
contains the reference trajectories/points that must be followed at time points 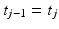 or over intervals
or over intervals ![$$[{t}_{j-1}, {t}_j]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq18.gif) . Note that the extended reference can be represented as the projection of a “virtual reference”,
. Note that the extended reference can be represented as the projection of a “virtual reference”, 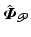 , denoted by
, denoted by 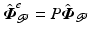 , however
, however 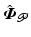 is not required in the control strategy. If the designer chooses
is not required in the control strategy. If the designer chooses 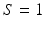 ,
, 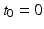 ,
, 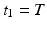 , and
, and 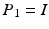 then (6.4) collapses to the standard form (4.3).
then (6.4) collapses to the standard form (4.3).6.2 Reduced Stimulation and Joint Subspaces
To reduce the number of degrees of freedom in problem (6.4) we can mimic the natural strategy of human motor control which involves a single neural command signal controlling multiple muscles. Each group of muscles working together is called a synergy, and the same muscle can potentially be employed within multiple synergies. To do this we introduce a set of 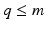 neural signals, denoted
neural signals, denoted ![$$\varvec{x} \in \mathscr {L}_2^{q}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq27.gif) . The mapping between
. The mapping between 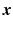 and the m muscle stimulation signals
and the m muscle stimulation signals ![$$\varvec{u} \in \mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq29.gif) , can be represented at time t by
, can be represented at time t by 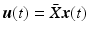 . Here
. Here 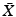 is a
is a 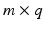 matrix with full column rank, with the jth column defining which muscles make up the jth synergy. The map between neural and muscle stimulation signals is therefore defined by
matrix with full column rank, with the jth column defining which muscles make up the jth synergy. The map between neural and muscle stimulation signals is therefore defined by 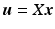 , with
, with
![$$\begin{aligned} X : \mathscr {L}_2^{q}[0,T] \rightarrow \mathscr {X}[0,T] : \varvec{x} \mapsto \varvec{u}, \; \varvec{u}(t) = \bar{X} \varvec{x}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ6.gif)
Here ![$$\mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq34.gif) is that subset of stimulation space
is that subset of stimulation space ![$$\mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq35.gif) which is achievable given the specified set of q synergistic muscle combinations, and is defined by
which is achievable given the specified set of q synergistic muscle combinations, and is defined by
![$$\begin{aligned} \mathscr {X}[0,T] := \left\{ \varvec{u} = X \varvec{x}, \; \varvec{x} \in \mathscr {L}_2^{q}[0,T] \right\} \subset \mathscr {L}_2^{m}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ7.gif)
The subspace ![$$\mathscr {X}[0,T] $$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq36.gif) is convex: to see this let
is convex: to see this let 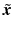 ,
, 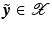 , then
, then 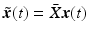 ,
, 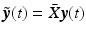 then
then ![$$\tilde{\varvec{x}}(t) + a (\tilde{\varvec{y}}(t) - \tilde{\varvec{x}}(t)) = X ( \varvec{x}(t) + a (\varvec{y}(t) - \varvec{x}(t)) ), \; a = [0,1]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq41.gif) . Since
. Since ![$$\varvec{x} + a (\varvec{y} - \varvec{x}) \in \mathscr {L}_2^{q}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq42.gif) it follows from (6.7) that
it follows from (6.7) that ![$$\tilde{\varvec{x}} + a (\tilde{\varvec{y}} - \tilde{\varvec{x}}) \in \mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq43.gif) .
.
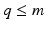 neural signals, denoted
neural signals, denoted ![$$\varvec{x} \in \mathscr {L}_2^{q}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq27.gif) . The mapping between
. The mapping between 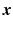 and the m muscle stimulation signals
and the m muscle stimulation signals ![$$\varvec{u} \in \mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq29.gif) , can be represented at time t by
, can be represented at time t by 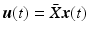 . Here
. Here 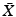 is a
is a 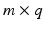 matrix with full column rank, with the jth column defining which muscles make up the jth synergy. The map between neural and muscle stimulation signals is therefore defined by
matrix with full column rank, with the jth column defining which muscles make up the jth synergy. The map between neural and muscle stimulation signals is therefore defined by 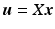 , with
, with![$$\begin{aligned} X : \mathscr {L}_2^{q}[0,T] \rightarrow \mathscr {X}[0,T] : \varvec{x} \mapsto \varvec{u}, \; \varvec{u}(t) = \bar{X} \varvec{x}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ6.gif)
(6.6)
![$$\mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq34.gif) is that subset of stimulation space
is that subset of stimulation space ![$$\mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq35.gif) which is achievable given the specified set of q synergistic muscle combinations, and is defined by
which is achievable given the specified set of q synergistic muscle combinations, and is defined by![$$\begin{aligned} \mathscr {X}[0,T] := \left\{ \varvec{u} = X \varvec{x}, \; \varvec{x} \in \mathscr {L}_2^{q}[0,T] \right\} \subset \mathscr {L}_2^{m}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ7.gif)
(6.7)
![$$\mathscr {X}[0,T] $$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq36.gif) is convex: to see this let
is convex: to see this let 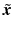 ,
, 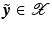 , then
, then 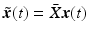 ,
, 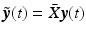 then
then ![$$\tilde{\varvec{x}}(t) + a (\tilde{\varvec{y}}(t) - \tilde{\varvec{x}}(t)) = X ( \varvec{x}(t) + a (\varvec{y}(t) - \varvec{x}(t)) ), \; a = [0,1]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq41.gif) . Since
. Since ![$$\varvec{x} + a (\varvec{y} - \varvec{x}) \in \mathscr {L}_2^{q}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq42.gif) it follows from (6.7) that
it follows from (6.7) that ![$$\tilde{\varvec{x}} + a (\tilde{\varvec{y}} - \tilde{\varvec{x}}) \in \mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq43.gif) .
.Operator X restricts the stimulation signal 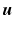 to belong to a subspace
to belong to a subspace ![$$\mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq45.gif) of
of ![$$\mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq46.gif) . However, we can also reduce the degree of freedom of control problem (6.4) by restricting the joint demand signal,
. However, we can also reduce the degree of freedom of control problem (6.4) by restricting the joint demand signal, 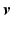 , generated by ILC to belong to a suitable subspace of
, generated by ILC to belong to a suitable subspace of ![$$\mathscr {L}_2^{p}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq48.gif) . To do this we introduce a set of q signals which represent synergies in joint space, and define the mapping between
. To do this we introduce a set of q signals which represent synergies in joint space, and define the mapping between ![$$\mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq49.gif) and the achievable subset of joint space by
and the achievable subset of joint space by
![$$\begin{aligned} W : \mathscr {L}_2^{q}[0,T] \rightarrow \mathscr {W}[0,T] : \varvec{r} \mapsto \varvec{v}, \; \varvec{v}(t) = \bar{W} \varvec{r}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ8.gif)
where 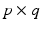 matrix W has full column rank. The corresponding joint subspace is
matrix W has full column rank. The corresponding joint subspace is
![$$\begin{aligned} \mathscr {W}[0,T] := \left\{ \varvec{v} = W \varvec{r}, \; \varvec{r} \in \mathscr {L}_2^{q}[0,T] \right\} \subset \mathscr {L}_2^{p}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ9.gif)
Embedding these subspaces into control problem (6.4) gives rise to:
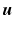 to belong to a subspace
to belong to a subspace ![$$\mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq45.gif) of
of ![$$\mathscr {L}_2^{m}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq46.gif) . However, we can also reduce the degree of freedom of control problem (6.4) by restricting the joint demand signal,
. However, we can also reduce the degree of freedom of control problem (6.4) by restricting the joint demand signal, 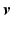 , generated by ILC to belong to a suitable subspace of
, generated by ILC to belong to a suitable subspace of ![$$\mathscr {L}_2^{p}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq48.gif) . To do this we introduce a set of q signals which represent synergies in joint space, and define the mapping between
. To do this we introduce a set of q signals which represent synergies in joint space, and define the mapping between ![$$\mathscr {L}^q_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq49.gif) and the achievable subset of joint space by
and the achievable subset of joint space by![$$\begin{aligned} W : \mathscr {L}_2^{q}[0,T] \rightarrow \mathscr {W}[0,T] : \varvec{r} \mapsto \varvec{v}, \; \varvec{v}(t) = \bar{W} \varvec{r}(t). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ8.gif)
(6.8)
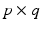 matrix W has full column rank. The corresponding joint subspace is
matrix W has full column rank. The corresponding joint subspace is![$$\begin{aligned} \mathscr {W}[0,T] := \left\{ \varvec{v} = W \varvec{r}, \; \varvec{r} \in \mathscr {L}_2^{q}[0,T] \right\} \subset \mathscr {L}_2^{p}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ9.gif)
(6.9)
Definition 6.1
6.3 Extended ILC Framework
Theorem 6.1
Consider the ILC update sequence
![$$\begin{aligned} \varvec{v}_{k+1}&= \varvec{v}_k + W L_k ( \varvec{e}_{k} )^e_{\mathscr {P}}, \quad \quad k = 0,1,\ldots , \quad \varvec{v}_0 \in \mathscr {W}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ13.gif)
If learning operator ![$$L_k : \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq55.gif) satisfies
satisfies
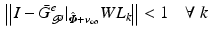
where the operator norm is induced from the inner product 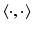 , then
, then
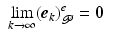
and, for 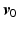 chosen sufficiently close to
chosen sufficiently close to 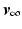 , the ILC update converges to
, the ILC update converges to
![$$\begin{aligned}&\lim _{k \rightarrow \infty } (\hat{\varvec{\varPhi }} + \varvec{v}_k) = W L_{\infty } (\bar{G}_{\mathscr {P}}^e |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty })^{-1} \hat{\varvec{\varPhi }}^e_{\mathscr {P}}, \quad \text {with} \quad \varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ16.gif)
Alternatively, if the learning operator 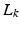 satisfies
satisfies
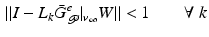
then, for 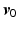 chosen sufficiently close to
chosen sufficiently close to 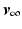 , the ILC update converges to
, the ILC update converges to
![$$\begin{aligned}&\lim _{k \rightarrow \infty } (\hat{\varvec{\varPhi }} + \varvec{v}_k) = W ( L_{\infty } \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W )^{-1} L_{\infty } \hat{\varvec{\varPhi }}^e_{\mathscr {P}} \quad \text {with} \quad \varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ18.gif)
![$$\begin{aligned} \varvec{v}_{k+1}&= \varvec{v}_k + W L_k ( \varvec{e}_{k} )^e_{\mathscr {P}}, \quad \quad k = 0,1,\ldots , \quad \varvec{v}_0 \in \mathscr {W}[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ13.gif)
(6.13)
![$$L_k : \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}] \rightarrow \mathscr {L}^{p}_2 [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq55.gif) satisfies
satisfies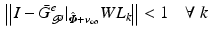
(6.14)
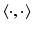 , then
, then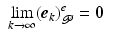
(6.15)
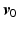 chosen sufficiently close to
chosen sufficiently close to 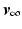 , the ILC update converges to
, the ILC update converges to![$$\begin{aligned}&\lim _{k \rightarrow \infty } (\hat{\varvec{\varPhi }} + \varvec{v}_k) = W L_{\infty } (\bar{G}_{\mathscr {P}}^e |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty })^{-1} \hat{\varvec{\varPhi }}^e_{\mathscr {P}}, \quad \text {with} \quad \varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ16.gif)
(6.16)
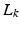 satisfies
satisfies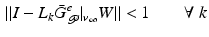
(6.17)
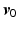 chosen sufficiently close to
chosen sufficiently close to 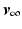 , the ILC update converges to
, the ILC update converges to![$$\begin{aligned}&\lim _{k \rightarrow \infty } (\hat{\varvec{\varPhi }} + \varvec{v}_k) = W ( L_{\infty } \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W )^{-1} L_{\infty } \hat{\varvec{\varPhi }}^e_{\mathscr {P}} \quad \text {with} \quad \varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ18.gif)
(6.18)
Proof
Update (6.13) is equivalent to applying 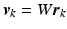 to system (6.3) where
to system (6.3) where
![$$\begin{aligned} \varvec{r}_{k+1} = \varvec{r}_k + L_k ( \varvec{e}_{k} )^e_{\mathscr {P}}, \quad \quad k = 0,1,\ldots , \quad \varvec{r}_0 \in \mathscr {L}_2^q[0,T] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ19.gif)
and hence ![$$\varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq63.gif) . The error dynamics locally satisfy
. The error dynamics locally satisfy
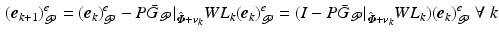 so if (6.14) holds, the extended error converges monotonically to zero since
so if (6.14) holds, the extended error converges monotonically to zero since
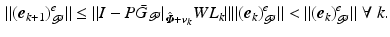
For 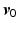 sufficiently close to
sufficiently close to 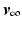 , then
, then 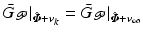 and
and 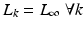 , and
, and
![$$\begin{aligned} \varvec{v}_{k+1}&= \varvec{v}_0 + W L_{\infty } \sum ^k_{i = 0} ( \varvec{e}_{i} )^e_{\mathscr {P}} = \varvec{v}_0 + W L_{\infty } \sum ^k_{i = 0} \big ( I - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty } \big )^i \nonumber \\[-0.4cm]&\quad \times \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} ( \hat{\varvec{\varPhi }} + \varvec{v}_0 ) \big ) \nonumber \\&= W L_{\infty } \sum ^k_{i = 0} \big ( I - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty } \big )^i \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - \hat{\varvec{\varPhi }} \nonumber \\[-0.9cm] \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ51.gif) so that if (6.14) holds
so that if (6.14) holds
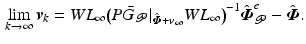
In addition, the input signals locally satisfy
![$$\begin{aligned} \varvec{r}_{k+1}&= \varvec{r}_{k} + L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} (\hat{\varvec{\varPhi }} + W \varvec{r}_k) \big ) \nonumber \\&= \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big ) \varvec{r}_{k} + L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\&= \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{k+1} \varvec{r}_0 \nonumber \\&\quad + \sum _{i = 0}^{k} \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^i L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\[-0.9cm] \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ52.gif) so that, if (6.17) is satisfied,
so that, if (6.17) is satisfied,
![$$\begin{aligned} \lim _{k \rightarrow \infty } \varvec{v}_k&= W \big ( L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{-1} L_{\infty } P \big ( \hat{\varvec{\varPhi }}_{\mathscr {P}} - \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\[-0.2cm]&= W \big ( L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{-1} L_{\infty } \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - \hat{\varvec{\varPhi }}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ22.gif)

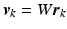 to system (6.3) where
to system (6.3) where![$$\begin{aligned} \varvec{r}_{k+1} = \varvec{r}_k + L_k ( \varvec{e}_{k} )^e_{\mathscr {P}}, \quad \quad k = 0,1,\ldots , \quad \varvec{r}_0 \in \mathscr {L}_2^q[0,T] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ19.gif)
(6.19)
![$$\varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq63.gif) . The error dynamics locally satisfy
. The error dynamics locally satisfy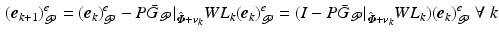
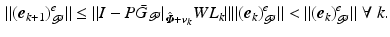
(6.20)
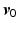 sufficiently close to
sufficiently close to 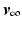 , then
, then 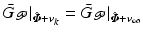 and
and 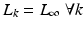 , and
, and![$$\begin{aligned} \varvec{v}_{k+1}&= \varvec{v}_0 + W L_{\infty } \sum ^k_{i = 0} ( \varvec{e}_{i} )^e_{\mathscr {P}} = \varvec{v}_0 + W L_{\infty } \sum ^k_{i = 0} \big ( I - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty } \big )^i \nonumber \\[-0.4cm]&\quad \times \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} ( \hat{\varvec{\varPhi }} + \varvec{v}_0 ) \big ) \nonumber \\&= W L_{\infty } \sum ^k_{i = 0} \big ( I - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W L_{\infty } \big )^i \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - \hat{\varvec{\varPhi }} \nonumber \\[-0.9cm] \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ51.gif)
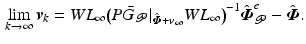
(6.21)
![$$\begin{aligned} \varvec{r}_{k+1}&= \varvec{r}_{k} + L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} (\hat{\varvec{\varPhi }} + W \varvec{r}_k) \big ) \nonumber \\&= \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big ) \varvec{r}_{k} + L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\&= \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{k+1} \varvec{r}_0 \nonumber \\&\quad + \sum _{i = 0}^{k} \big ( I - L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^i L_{\infty } \big ( \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\[-0.9cm] \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ52.gif)
![$$\begin{aligned} \lim _{k \rightarrow \infty } \varvec{v}_k&= W \big ( L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{-1} L_{\infty } P \big ( \hat{\varvec{\varPhi }}_{\mathscr {P}} - \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} \hat{\varvec{\varPhi }} \big ) \nonumber \\[-0.2cm]&= W \big ( L_{\infty } P \bar{G}_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_{\infty }} W \big )^{-1} L_{\infty } \hat{\varvec{\varPhi }}^e_{\mathscr {P}} - \hat{\varvec{\varPhi }}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ22.gif)
(6.22)

Within Theorem 6.1, the linearized extended plant operator is defined by:
Lemma 6.1
Around operating point 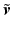 the dynamics
the dynamics 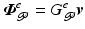 are captured by the map
are captured by the map ![$$\bar{G}^e_{\mathscr {P}} |_{\tilde{\varvec{v}}} : \mathscr {L}_2^{p}[0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq71.gif) defined by
defined by
![$$\begin{aligned}&\bar{G}^e_{\mathscr {P}} |_{\tilde{\varvec{v}}} \varvec{v} = \left[ \begin{array}{c} (P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_1 \varvec{v} \\ \vdots \\ (P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_S \varvec{v} \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ23.gif)
where
![$$\begin{aligned} ((P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_j \varvec{v})(t) = {P_j} {\int _0^{t}} C(t) \varGamma ( t, \tau ) B( \tau ) \varvec{v} (\tau ) \mathrm {d} \tau , \quad t \in [{t_{j-1}}, {t_j}], \; j = 1, \ldots , S \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ24.gif)
in which A(t), B(t), C(t) and 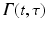 are defined in Lemma 4.2.
are defined in Lemma 4.2.
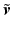 the dynamics
the dynamics 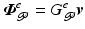 are captured by the map
are captured by the map ![$$\bar{G}^e_{\mathscr {P}} |_{\tilde{\varvec{v}}} : \mathscr {L}_2^{p}[0,T] \rightarrow \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq71.gif) defined by
defined by![$$\begin{aligned}&\bar{G}^e_{\mathscr {P}} |_{\tilde{\varvec{v}}} \varvec{v} = \left[ \begin{array}{c} (P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_1 \varvec{v} \\ \vdots \\ (P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_S \varvec{v} \end{array} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ23.gif)
(6.23)
![$$\begin{aligned} ((P \bar{G}_{\mathscr {P}} |_{\tilde{\varvec{v}}} )_j \varvec{v})(t) = {P_j} {\int _0^{t}} C(t) \varGamma ( t, \tau ) B( \tau ) \varvec{v} (\tau ) \mathrm {d} \tau , \quad t \in [{t_{j-1}}, {t_j}], \; j = 1, \ldots , S \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ24.gif)
(6.24)
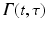 are defined in Lemma 4.2.
are defined in Lemma 4.2.Theorem 6.2
Within (6.13), let the ILC operator be given by
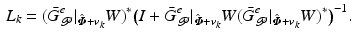
Setting 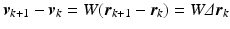 , this is equivalent to solving the underlying subspace problem
, this is equivalent to solving the underlying subspace problem
![$$\begin{aligned} \varDelta \varvec{r}_k := \min _{\varDelta \varvec{r}} \Big \{ \Vert \varDelta \varvec{r} \Vert ^2_{[R]} + \Vert (\varvec{e}_k)^e_{\mathscr {P}} - \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \varDelta \varvec{r} \Vert ^2_{Q} \Big \}, \quad \quad \varvec{r}_0 = \varvec{0}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ26.gif)
where ![$$[R] = W^\top R W$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq74.gif) , with symmetric positive-definite weights Q and R.
, with symmetric positive-definite weights Q and R.
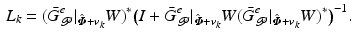
(6.25)
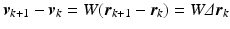 , this is equivalent to solving the underlying subspace problem
, this is equivalent to solving the underlying subspace problem![$$\begin{aligned} \varDelta \varvec{r}_k := \min _{\varDelta \varvec{r}} \Big \{ \Vert \varDelta \varvec{r} \Vert ^2_{[R]} + \Vert (\varvec{e}_k)^e_{\mathscr {P}} - \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \varDelta \varvec{r} \Vert ^2_{Q} \Big \}, \quad \quad \varvec{r}_0 = \varvec{0}. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ26.gif)
(6.26)
![$$[R] = W^\top R W$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq74.gif) , with symmetric positive-definite weights Q and R.
, with symmetric positive-definite weights Q and R.Proof
If 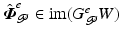 for all possible
for all possible 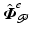 , it follows that
, it follows that 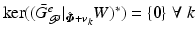 . If
. If 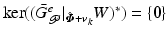 the solution to (6.26) is
the solution to (6.26) is 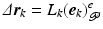 with
with 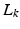 given by (6.25) which satisfies (6.14) with limiting solution
given by (6.25) which satisfies (6.14) with limiting solution
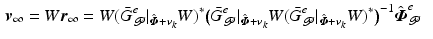
corresponding to
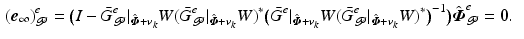 The Lagrangian associated with minimum energy problem (6.27) is just, with Lagrange multiplier
The Lagrangian associated with minimum energy problem (6.27) is just, with Lagrange multiplier ![$$\varvec{\lambda } \in \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq83.gif) ,
,
Get Clinical Tree app for offline access

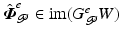 for all possible
for all possible 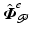 , it follows that
, it follows that 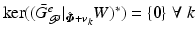 . If
. If 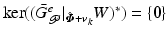 the solution to (6.26) is
the solution to (6.26) is 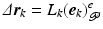 with
with 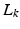 given by (6.25) which satisfies (6.14) with limiting solution
given by (6.25) which satisfies (6.14) with limiting solution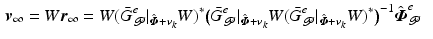
(6.29)
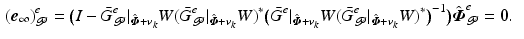
![$$\varvec{\lambda } \in \mathscr {L}_2^{p_1} [0, t_1] \times \cdots \times \mathscr {L}_2^{p_{S}} [t_{S-1}, t_{S}]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq83.gif) ,
,Lemma 6.2
Choosing 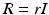 ,
, 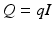 ,
, 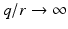 , the ILC update (6.25) realizes minimizing solutions (6.29) and (6.31) respectively in a single ILC iteration. In both cases the required term
, the ILC update (6.25) realizes minimizing solutions (6.29) and (6.31) respectively in a single ILC iteration. In both cases the required term 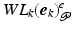 in (4.4) can be computed efficiently as the outcome,
in (4.4) can be computed efficiently as the outcome, 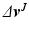 , of J iterations of the computation
, of J iterations of the computation
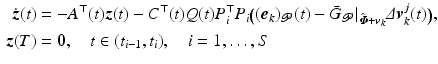
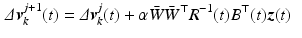
where J and ![$$\alpha > 0$$” src=”/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq96.gif”></SPAN> are sufficiently large and small values respectively.</DIV></DIV><br />
<DIV id=FPar8 class=]()
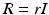 ,
, 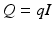 ,
, 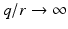 , the ILC update (6.25) realizes minimizing solutions (6.29) and (6.31) respectively in a single ILC iteration. In both cases the required term
, the ILC update (6.25) realizes minimizing solutions (6.29) and (6.31) respectively in a single ILC iteration. In both cases the required term 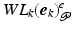 in (4.4) can be computed efficiently as the outcome,
in (4.4) can be computed efficiently as the outcome, 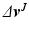 , of J iterations of the computation
, of J iterations of the computation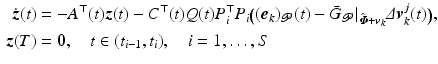
(6.33)
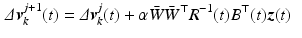
(6.34)
Proof
As 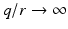 , update (6.25) and (6.30) respectively converge to
, update (6.25) and (6.30) respectively converge to
![$$\begin{aligned}&L_k = (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \big ( \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \big )^{-1}, \quad \text {and} \nonumber \\[-0.1cm]&L_k = \big ( (\bar{G}^e_{ \mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \big )^{-1} (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ55.gif) which it is shown in [1] correspond to solutions of the minimum energy problem
which it is shown in [1] correspond to solutions of the minimum energy problem
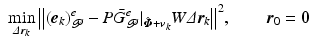
using gradient based ILC [2]. This equates to 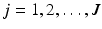 iterations of update
iterations of update
![$$\begin{aligned}&\varDelta \varvec{r}_k^{j+1} = \varDelta \varvec{r}_k^j + \alpha ( P \bar{G}^e|_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W )^*\big ( (\varvec{e}_k)^e_{\mathscr {P}} - P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \varDelta \varvec{r}_k^j \big ) \nonumber \\[-0.1cm] \Rightarrow&\varDelta \varvec{v}_k^{j+1} = \varDelta \varvec{v}_k^j + \alpha W ( P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W )^*\big ( (\varvec{e}_k)^e_{\mathscr {P}} - P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} \varDelta \varvec{v}_k^j \big ). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ36.gif)
Operator 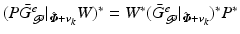 is defined by a relation of the form
is defined by a relation of the form 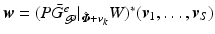 as the continuous solution of the costate equation
as the continuous solution of the costate equation
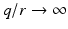 , update (6.25) and (6.30) respectively converge to
, update (6.25) and (6.30) respectively converge to![$$\begin{aligned}&L_k = (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \big ( \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \big )^{-1}, \quad \text {and} \nonumber \\[-0.1cm]&L_k = \big ( (\bar{G}^e_{ \mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \big )^{-1} (\bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W)^{*} \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ55.gif)
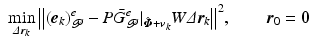
(6.35)
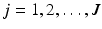 iterations of update
iterations of update![$$\begin{aligned}&\varDelta \varvec{r}_k^{j+1} = \varDelta \varvec{r}_k^j + \alpha ( P \bar{G}^e|_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W )^*\big ( (\varvec{e}_k)^e_{\mathscr {P}} - P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \varDelta \varvec{r}_k^j \big ) \nonumber \\[-0.1cm] \Rightarrow&\varDelta \varvec{v}_k^{j+1} = \varDelta \varvec{v}_k^j + \alpha W ( P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} W )^*\big ( (\varvec{e}_k)^e_{\mathscr {P}} - P \bar{G}^e_{\mathscr {P}} |_{\hat{\varvec{\varPhi }} + \varvec{v}_k} \varDelta \varvec{v}_k^j \big ). \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ36.gif)
(6.36)
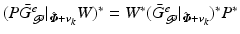 is defined by a relation of the form
is defined by a relation of the form 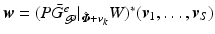 as the continuous solution of the costate equation
as the continuous solution of the costate equation
![$$\mathscr {X}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq51.gif)
![$$\begin{aligned} \varvec{v}_{\infty } := \min _{\varvec{v}} J( \varvec{v} ), \;\;\;\;\; J( \varvec{v} ) = \big \Vert \overbrace{ \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - G_{\mathscr {P}}^e (\hat{\varvec{\varPhi }} + \varvec{v}) }^{ \varvec{e}_{\mathscr {P}}^e} \big \Vert ^2, \quad \varvec{u}_k \in \mathscr {X}[0,T] \; \forall \; k \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ10.gif)
![$$\begin{aligned} K : \mathscr {L}^p[0,T] \mapsto \mathscr {X}[0,T] \; : K = X K_X, \; K_X : \mathscr {L}^p[0,T] \rightarrow \mathscr {L}^q[0,T]. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ11.gif)
![$$\mathscr {W}[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq52.gif)
![$$\begin{aligned} \varvec{v}_{\infty } := \min _{\varvec{v}} J( \varvec{v} ), \;\;\;\;\; J( \varvec{v} ) = \big \Vert \underbrace{ \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - G_{\mathscr {P}}^e (\hat{\varvec{\varPhi }} + \varvec{v}) }_{\varvec{e}_{\mathscr {P}}^e} \big \Vert ^2, \quad \varvec{v}_k \in \mathscr {W}[0,T] \; \forall \; k. \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ12.gif)
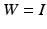
![$$\mathscr {W} = \mathscr {L}^p_2[0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq54.gif)
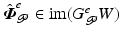
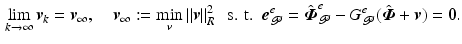
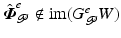
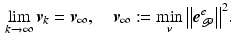
![$$\begin{aligned} \mathscr {L}( \varvec{r}, \varvec{\lambda } )&= \Vert \varvec{v} \Vert _{R}^2 + 2 <\varvec{\lambda }, \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - \bar{G}^e | _{\hat{\varvec{\varPhi }} + \varvec{v}_k} \varvec{v}>\, = \Vert \varvec{r} \Vert _{[R]}^2 + 2 <\varvec{\lambda }, \hat{\varvec{\varPhi }}_{\mathscr {P}}^e - \bar{G}^e | _{\hat{\varvec{\varPhi }} + \varvec{v}_k} W \varvec{r}> \nonumber \end{aligned}$$” src=”/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_Equ54.gif”></DIV></DIV></DIV>which has a stationary point when <SPAN id=IEq84 class=InlineEquation><IMG alt=](/wp-content/uploads/2016/09/A352940_1_En_6_Chapter_IEq84.gif) and
and