, 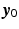 .
.
The ultimate goal of this rehabilitation technology is to translate into patients’ homes, where it can be used without direct supervision from a therapist over longer training periods. Further developments are required to facilitate this, and include:
1.
Lengthy and often fatiguing model identification tests (that may require a therapist to administer) must be reduced or eliminated.
2.
Control scheme parameter tuning must automatically compensate for physiological changes such as fatigue, spasticity and change in electrode position.
3.
ES hardware must be easy to don and doff, and incorporate as few components and wires as possible.
4.
Patient-specific motor re-learning models are necessary to enable tasks and treatment modalities to be automatically chosen to maximize long-term treatment outcomes.
5.
Expensive components (e.g. dSPACE, touch table, SaeboMAS) should be replaced with affordable alternatives (e.g. embedded ‘system on chip’ hardware, tablet/smart TV/smartphone, Bakx Magic Arm/Focal Meditech Balancer/Sammons Preston Stable Slide).
These developments are aligned with the needs of patients, carers and healthcare professionals that have been identified in [1], and in questionnaires reported in [2]. The next section describes an approach which has potential to address points (1) and (2), and the subsequent section provides a route to address point (3).
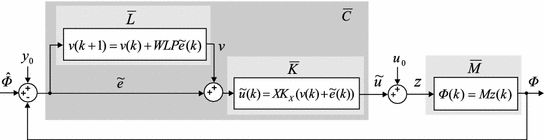

Fig. 10.1
General feedback and ILC control scheme in lifted framework with external disturbance
10.1 Elimination of Identification and Manual Controller Tuning
The control design framework developed in this book involves obtaining a plant model description, 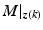 , that captures the plant dynamics about the operating point,
, that captures the plant dynamics about the operating point, 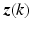 , corresponding to the kth task attempt. The feedback and ILC controllers K and L are then computed using this model. In the case of single-pad electrodes, feedback controller K may alternatively be designed using a global model, M, but L must still be designed using the linearized model
, corresponding to the kth task attempt. The feedback and ILC controllers K and L are then computed using this model. In the case of single-pad electrodes, feedback controller K may alternatively be designed using a global model, M, but L must still be designed using the linearized model 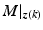 .
.
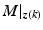 , that captures the plant dynamics about the operating point,
, that captures the plant dynamics about the operating point, 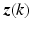 , corresponding to the kth task attempt. The feedback and ILC controllers K and L are then computed using this model. In the case of single-pad electrodes, feedback controller K may alternatively be designed using a global model, M, but L must still be designed using the linearized model
, corresponding to the kth task attempt. The feedback and ILC controllers K and L are then computed using this model. In the case of single-pad electrodes, feedback controller K may alternatively be designed using a global model, M, but L must still be designed using the linearized model 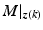 .
.While this provides a powerful framework to enable ES to support functional movements, the need to identify the underlying model is a significant limitation. For example, in the studies of Chaps. 7 and 9 identification took approximately 15 min and was conducted only at the start of each treatment session. Similarly, time constraints also meant that identification of an array model between trials was not undertaken, and incurred further reduction in tracking accuracy. This was also the reason the fully decoupled design of Theorem 9.2 was used instead of the partially decoupled design of Theorem 9.1. A further issue is the presence of fatigue and spasticity which can rapidly change the stimulated arm dynamics leading to degraded levels of performance. It is therefore desirable to reduce, or ideally remove, the need for model identification, while at the same time adapting the controller to maintain satisfactory performance.
An obvious solution is to expand the framework to automatically chose the ‘best’ model that matches observed input-output data from a bank of possible models that are specified by the designer before the experiment or treatment session begins. Such a framework, however, requires carefully selection of the candidate model set, controller properties and switching in order to preserve robust stability bounds (as specified by tracking performance bound (4.43) of Theorem 4.5).
A suitable framework has recently become available in the form of estimation based multiple model switched adaptive control (EMMSAC) developed in [3, 4]. EMMSAC uses a bank of Kalman filters to assess the performance of a set of candidate plant models, and the controller corresponding to the most suitable plant model is then switched into closed-loop. Distinct from other switched multiple model approaches, robust performance bounds for EMMSAC are invariant to the size of the set of possible models chosen by the designer. This means that adding more candidate models does not degrade the resulting closed-loop performance properties. Feasibility of using EMMSAC for ES-based upper limb rehabilitation was established in [5], where it was employed to assist participants perform isometric tracking tasks using ES, while supported by a robotic arm. Results with five unimpaired participants showed that it is possible to eliminate model identification while employing closed-loop ES controllers that maintain high performance in the presence of rapidly changing system dynamics. The axiomatic framework of EMMSAC places no restriction on control structure or plant uncertainty form, but delivers explicit guarantees for robust performance. A comprehensive framework for extension to ILC has recently been formulated in [6] and is termed estimation based multiple model ILC (EMMILC). Experimental results confirm further increased tracking performance due to the addition of ILC.
Acting in the lifted space, EMMILC employs exactly the same lifted structure that has been used extensively in this book to perform stability analysis. However, instead of a single model and controller pair 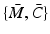 defined by (4.34)–(4.36) we now define n pairs
defined by (4.34)–(4.36) we now define n pairs 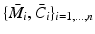 before the experiment or treatment session begins. Note that for simplicity they and the true plant,
before the experiment or treatment session begins. Note that for simplicity they and the true plant, 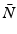 , are assumed to be LTI. For each model
, are assumed to be LTI. For each model 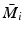 in our candidate model set
in our candidate model set 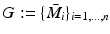 we implement an estimator
we implement an estimator 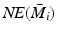 which uses observations
which uses observations 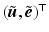 to generate a residual
to generate a residual ![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq13.gif) at the end of trial k. The size of
at the end of trial k. The size of ![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq14.gif) corresponds to the norm of the minimum disturbance needed to explain the observed signals if
corresponds to the norm of the minimum disturbance needed to explain the observed signals if 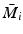 was the true plant (
was the true plant (![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq16.gif) can readily be computed using a Kalman filter running over
can readily be computed using a Kalman filter running over ![$$t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq17.gif) on trial k). These values are fed to the minimization operator H, which returns the index,
on trial k). These values are fed to the minimization operator H, which returns the index, 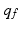 , of the plant with minimal residual. The free switching signal
, of the plant with minimal residual. The free switching signal 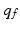 is then delayed long enough to prevent instability effects caused by rapid switching, and thereby ensure overall convergence of the closed-loop signals. For this purpose we implement a delay operator D which ensures that a delay of
is then delayed long enough to prevent instability effects caused by rapid switching, and thereby ensure overall convergence of the closed-loop signals. For this purpose we implement a delay operator D which ensures that a delay of 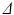 iterations must elapse before another is permitted. The signal q then determines the controller choice
iterations must elapse before another is permitted. The signal q then determines the controller choice 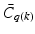 (corresponding to the selected plant) which is switched into closed-loop. Together these components comprise the switching operator
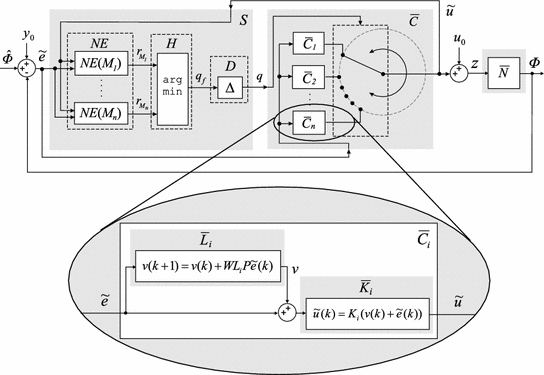
(corresponding to the selected plant) which is switched into closed-loop. Together these components comprise the switching operator 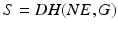 shown in Fig. 10.2. The table summarizes the structural requirements that specify the switching algorithm illustrated in Fig. 10.2, where restriction operator
shown in Fig. 10.2. The table summarizes the structural requirements that specify the switching algorithm illustrated in Fig. 10.2, where restriction operator 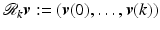 .
.
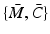 defined by (4.34)–(4.36) we now define n pairs
defined by (4.34)–(4.36) we now define n pairs 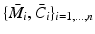 before the experiment or treatment session begins. Note that for simplicity they and the true plant,
before the experiment or treatment session begins. Note that for simplicity they and the true plant, 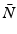 , are assumed to be LTI. For each model
, are assumed to be LTI. For each model 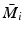 in our candidate model set
in our candidate model set 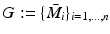 we implement an estimator
we implement an estimator 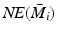 which uses observations
which uses observations 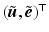 to generate a residual
to generate a residual ![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq13.gif) at the end of trial k. The size of
at the end of trial k. The size of ![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq14.gif) corresponds to the norm of the minimum disturbance needed to explain the observed signals if
corresponds to the norm of the minimum disturbance needed to explain the observed signals if 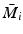 was the true plant (
was the true plant (![$$r_{i}[k]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq16.gif) can readily be computed using a Kalman filter running over
can readily be computed using a Kalman filter running over ![$$t \in [0,T]$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq17.gif) on trial k). These values are fed to the minimization operator H, which returns the index,
on trial k). These values are fed to the minimization operator H, which returns the index, 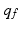 , of the plant with minimal residual. The free switching signal
, of the plant with minimal residual. The free switching signal 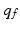 is then delayed long enough to prevent instability effects caused by rapid switching, and thereby ensure overall convergence of the closed-loop signals. For this purpose we implement a delay operator D which ensures that a delay of
is then delayed long enough to prevent instability effects caused by rapid switching, and thereby ensure overall convergence of the closed-loop signals. For this purpose we implement a delay operator D which ensures that a delay of 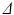 iterations must elapse before another is permitted. The signal q then determines the controller choice
iterations must elapse before another is permitted. The signal q then determines the controller choice 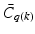 (corresponding to the selected plant) which is switched into closed-loop. Together these components comprise the switching operator
(corresponding to the selected plant) which is switched into closed-loop. Together these components comprise the switching operator 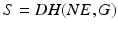 shown in Fig. 10.2. The table summarizes the structural requirements that specify the switching algorithm illustrated in Fig. 10.2, where restriction operator
shown in Fig. 10.2. The table summarizes the structural requirements that specify the switching algorithm illustrated in Fig. 10.2, where restriction operator 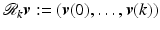 .
.
Fig. 10.2
EMMILC structure: switch 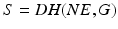 outputs switching signal q to determine which atomic controller choice
outputs switching signal q to determine which atomic controller choice 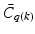 to switch into closed-loop. With no switching (q fixed), this corresponds to the framework of Chap. 6
to switch into closed-loop. With no switching (q fixed), this corresponds to the framework of Chap. 6
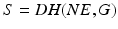 outputs switching signal q to determine which atomic controller choice
outputs switching signal q to determine which atomic controller choice 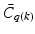 to switch into closed-loop. With no switching (q fixed), this corresponds to the framework of Chap. 6
to switch into closed-loop. With no switching (q fixed), this corresponds to the framework of Chap. 6 ![$$\begin{aligned} \text {Controller:} \quad&\bar{C} : \tilde{\varvec{e}} \mapsto \tilde{\varvec{u}} : \tilde{\varvec{u}}(k) = \bar{C}_{q(k)} \Big [ \Big \{ \begin{array}{ll} 0 &{}\text {if} \quad i < k_s \\ \tilde{\varvec{e}}(k) &{}\text {if} \quad i \ge k_s \end{array} \Big ] (k) \nonumber \\ \text {Estimator:} \quad&NE : r_{i}[k] = \inf \Big \{ \Big \Vert \begin{array}{c} \varvec{u}_0 \\ \varvec{y}_0 \end{array} \Big \Vert : \mathscr {R}_k (\varvec{y}_0 + \varvec{\varPhi } - \tilde{\varvec{e}}) = \mathscr {R}_k \bar{M}_i (\varvec{u}_0 - \tilde{\varvec{u}}) \Big \} \nonumber \\ \text {Minimizer:} \quad&H : q_f(k):= \min _{1 \le i \le n} r_{i}[k],\ \forall k \in \mathbb {N} \nonumber \\ \text {Delay:} \quad&D : q(k):= \Big \{ \begin{array}{cl}q_f(k) &{}\mathrm{if}\; k-k_s(k)\ge \varDelta \\ q(k_s(k)) &{}\mathrm{else}, \quad k_s(k):=\max \{ i \le k,\ q(i) \ne q(i-1) \} \end{array} \nonumber \end{aligned}$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_Equ6.gif)
The comprehensive nature of the axiomatic EMMILC framework of [6] means that there are numerous possible design options with which to specify each controller and estimator. A possible procedure that is appropriate to ES-based rehabilitation is outlined below:
Procedure 10
(EMMILC design procedure)
Select an uncertainty set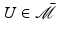 we seek to control. This is the smallest set that contains the true plant description
we seek to control. This is the smallest set that contains the true plant description 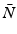 . Here
. Here 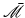 is the set of all lifted LTI models
is the set of all lifted LTI models ![$$\mathscr {L}^m_2[0,T] \times \mathbb {N} \rightarrow \mathscr {L}^p_2[0,T] \times \mathbb {N}$$](/wp-content/uploads/2016/09/A352940_1_En_10_Chapter_IEq29.gif) (which can be directly generated from their non-lifted counterparts
(which can be directly generated from their non-lifted counterparts 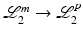 ).
).
Select a candidate model set,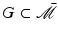 , which satisfies the condition
, which satisfies the condition
This specifies a maximum distance of
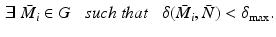
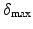 between models, measured using the gap metric (precise computation of
between models, measured using the gap metric (precise computation of 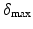 is given in [6]).
is given in [6]).
Associate each model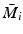 with a stabilizing controller
with a stabilizing controller 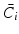 using a control design procedure
using a control design procedure 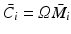 . If hardware allows, then each controller can be computed individually. Alternatively we can select a minimal set of controllers that stabilizes each element in U (computed using robust stability bound (4.42)), and associate multiple estimators with the same controller.
. If hardware allows, then each controller can be computed individually. Alternatively we can select a minimal set of controllers that stabilizes each element in U (computed using robust stability bound (4.42)), and associate multiple estimators with the same controller.
Recall that robust performance bounds computed using (4.43) for the case of a fixed controller 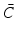 determine how closely the true plant maintains its operating point in the presence of external disturbance. These bounds take the form
determine how closely the true plant maintains its operating point in the presence of external disturbance. These bounds take the form
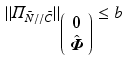 with explicit values of
with explicit values of 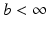 computed in Sects. 4.4 and 6.4. From (4.42), these hold provided the model is sufficiently close to the true plant
computed in Sects. 4.4 and 6.4. From (4.42), these hold provided the model is sufficiently close to the true plant 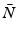 , thereby quantifying robust stability. EMMILC provides the following equivalent condition which holds across the entire uncertainty space U.
, thereby quantifying robust stability. EMMILC provides the following equivalent condition which holds across the entire uncertainty space U.
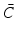 determine how closely the true plant maintains its operating point in the presence of external disturbance. These bounds take the form
determine how closely the true plant maintains its operating point in the presence of external disturbance. These bounds take the form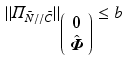
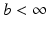 computed in Sects. 4.4 and 6.4. From (4.42), these hold provided the model is sufficiently close to the true plant
computed in Sects. 4.4 and 6.4. From (4.42), these hold provided the model is sufficiently close to the true plant 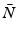 , thereby quantifying robust stability. EMMILC provides the following equivalent condition which holds across the entire uncertainty space U.
, thereby quantifying robust stability. EMMILC provides the following equivalent condition which holds across the entire uncertainty space U.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


