(7.1)
where vj(xyz) are the three dimensional coordinates of the nodes in the finite element mesh, v jd is the corresponding bone density at that node, j = 1,…, number of nodes in the finite element mesh, and i = 1…n = 7 denote each femur in the training set [76]. The mean finite element model of all femurs in the training set is then defined as:
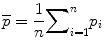
(7.2)
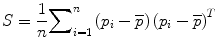
(7.3)
Principal components analysis (PCA) of S results in a set of eigenvalues (λi) and eigenvectors (q i ) [72] that are the principal directions of a shape and bone density space centered at 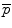 . Each eigenvalue defines the variance of the finite element mesh and corresponding bone density values from the mean in the direction of the corresponding eigenvector. The proportion of the total variance described by each eigenvector is equal to its corresponding eigenvalue normalized by the total variance (sum of all eigenvalues). The finite element mesh with associated bone density for each bone in the training set is now described as a statistical shape and density model (SSDM):
. Each eigenvalue defines the variance of the finite element mesh and corresponding bone density values from the mean in the direction of the corresponding eigenvector. The proportion of the total variance described by each eigenvector is equal to its corresponding eigenvalue normalized by the total variance (sum of all eigenvalues). The finite element mesh with associated bone density for each bone in the training set is now described as a statistical shape and density model (SSDM):
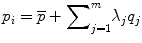
where λj are eigenvalues corresponding to the q i eigenvectors.
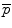 . Each eigenvalue defines the variance of the finite element mesh and corresponding bone density values from the mean in the direction of the corresponding eigenvector. The proportion of the total variance described by each eigenvector is equal to its corresponding eigenvalue normalized by the total variance (sum of all eigenvalues). The finite element mesh with associated bone density for each bone in the training set is now described as a statistical shape and density model (SSDM):
. Each eigenvalue defines the variance of the finite element mesh and corresponding bone density values from the mean in the direction of the corresponding eigenvector. The proportion of the total variance described by each eigenvector is equal to its corresponding eigenvalue normalized by the total variance (sum of all eigenvalues). The finite element mesh with associated bone density for each bone in the training set is now described as a statistical shape and density model (SSDM):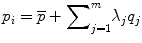
(7.4)
Multiple finite element models were developed using:
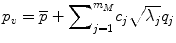
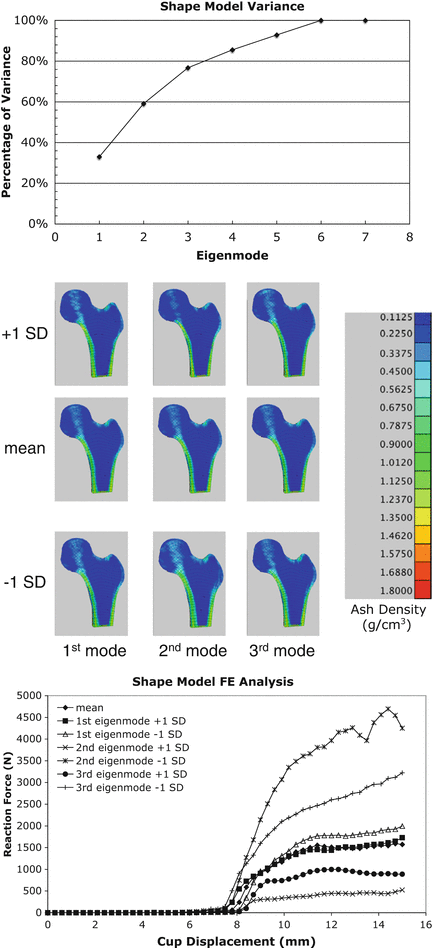
where m M is the number of major eigenvalues (the eigenmodes that describe greater than 75 % of the total training set variability), p v is a vector containing coordinates and apparent bone density value for all nodes in the FE model, and deviation from the average femur was determined as the sum of the products of a set of scalars, c j , and SSDM standard deviations, 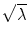 , along the q i direction [87]. FE models were developed for the mean geometry and bone density distribution as well as one each investigating the effects of ±1 standard deviation (SD) for each major independent eigenmode (Fig. 7.1).
, along the q i direction [87]. FE models were developed for the mean geometry and bone density distribution as well as one each investigating the effects of ±1 standard deviation (SD) for each major independent eigenmode (Fig. 7.1).
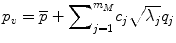
(7.5)
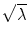 , along the q i direction [87]. FE models were developed for the mean geometry and bone density distribution as well as one each investigating the effects of ±1 standard deviation (SD) for each major independent eigenmode (Fig. 7.1).
, along the q i direction [87]. FE models were developed for the mean geometry and bone density distribution as well as one each investigating the effects of ±1 standard deviation (SD) for each major independent eigenmode (Fig. 7.1).
Fig. 7.1
Top: the SSDM describes over 75 % of the variability in femur shape and BMD distribution using the mean and first three principal components. Middle: clear differences are seen in the proximal femur geometry and BMD distribution (as indicated by the fringe plot). Bottom: finite element models efficiently created using the SSDM were used to predict proximal femur strength in the fall loading condition
In this analysis, elastic- plastic, linear hardening material behavior was assumed. Isotropic elastic moduli and ultimate stress values were determined as functions of ash density for all bone elements using empirical relationships [88]. Post-yield hardening moduli were set as 10 % of the elastic moduli. The models were oriented in a fall position [89, 90], the nodes representing the distal extent of the model at the greater trochanter were fixed, and a uniform displacement was applied through a flexible cup that contacted the femoral head. Models were solved using LS-DYNA (LSTC, Livermore, CA) on a Linux cluster and the vertical reaction force at the greater trochanter was recorded.
Principal components analysis of the statistical shape and density model demonstrated that 78 % of the variation in the set of 7 human proximal femur finite element models was captured by the first three independent modes of variation (eigenmodes) (Fig. 7.1). The finite element model representing the mean – 1 SD variation in the second eigenmode resulted in an increase in neck angle length, decrease in neck-shaft angle, increase in neck diameter, and an increase in cortex width (Fig. 7.2), all of which have been shown to decrease fracture risk [17, 30–36]. This independent mode of variation (eigenmode) resulted in the greatest predicted maximum load in a simulated fall configuration (Fig. 7.2). Thus, this modeling approach directly relates variations in bone geometry and bone density to bone strength through a high fidelity predictive engineering model. The advantage of the approach described herein is that a physics based predictive finite element model is used to directly assess bone strength, rather than a statistical correlation based on epidemiological data of fracture incidents, bone density measures, and geometry in a given population.
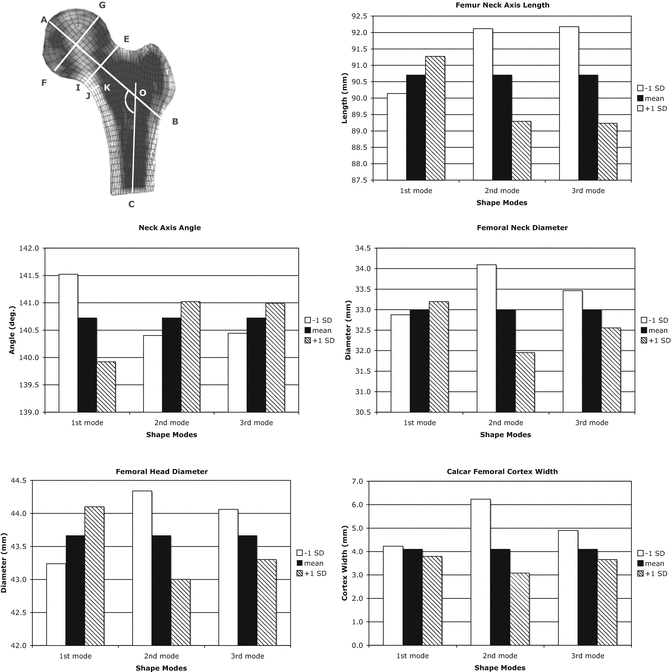

Fig. 7.2
Measures of proximal femur geometry determined for finite element models based on the statistical shape model of the proximal femur. The principal modes of variation from the mean represented by the shape model eigenvalues and eigenvectors generally have no direct physical meaning. However, by tracking the locations of specific points in the FE models that represent common measures of proximal femur geometry, the physical significance of each eigenmode can be discerned. Top Left: cross sectional view of a proximal femur FE model indicating definitions of typical proximal femur geometry measures. A–B femoral neck axis length, AOC neck-shaft angle, E–I femoral neck diameter, G–F femoral head diameter, J–K calcar femoral cortex width; Top right: proximal femur neck axis length; Middle Left: Proximal femur neck axis angle; Middle Right: proximal femur neck axis diameter; Bottom Left: femoral head diameter; Bottom Right: calcar femoral cortex width
A set of verification experiments was performed to verify the performance of the SSDM based finite element model predictions of femur strength. The femurs used to create the SSDM were sectioned transversely at a distance of four inches below the lesser trochanter. The distal portion of the proximal shaft was cleaned and embedded in PMMA within custom cylindrical mounting cups (Fig. 7.3). Using a custom fixture, each femur was mounted in a servo-hydraulic materials test machine (Instron, Canton, MA) in the fall loading configuration [89, 90]. Displacement was applied to the head of the femur through a rubber cup at a rate of 9.94 mm/s to a total displacement of 35 mm. The average maximum load recorded for the set of seven femurs was 1821.4 N +/− 1065.4 N similar to but slightly lower than the average SSDM FE model predictions of 1852.0 N+/− 1129.0 N.
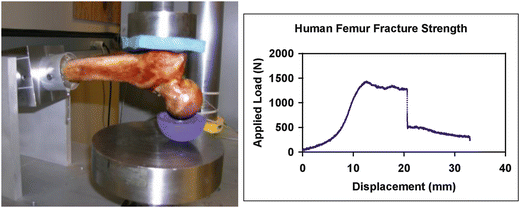

Fig. 7.3
Left: femur experimental test configuration. The human femur was loaded in a simulated fall configuration. Right: the measure load versus displacement response of the proximal femur. The load configuration resulted in an intertrochanteric fracture
7.7 Probabilistic Modeling Accounts for Biological Variability and Uncertainty in Data Parameters
All of the applications of engineering models to predict bone strength fail to account for the inherent variability in biological materials and structures as well as uncertainty in contained in our ability to directly measure these properties in-vivo. In many structural systems, there is a great deal of uncertainty associated with the environment in which the structure is required to function, the material properties of the system components, and in the structure itself (i.e. geometry). This variability or uncertainty has a direct effect on the ability to predict the structural response of the system and therefore its reliability [91–93]. Biological systems are a prime example: uncertainty and variability exist in the physical and mechanical properties of bone tissue and geometry of the bone, ligaments, cartilage, as well as uncertainty in joint and muscle loads. Since these quantities are used as input variables to finite element models, the predicted model response or performance will also be uncertain. Deterministic analyses, the class to which current applications of FEA to predict fracture risk belong, cannot quantify failure probabilities [92, 94, 95] because they do not include statistical information that describes the structure and material behavior. The recognition that predicting the probability of failure requires the use of probabilistic analysis techniques is a major motivation for this work.
Probabilistic analyses incorporate statistical information describing the materials, structural configuration, and environment from the outset whereas deterministic analyses discard this data. Modeling material behavior, structural geometry, and environmental loads and boundary conditions using random variables captures this statistical information. Using an appropriate performance function such as a simple strength-stress function, the probability of failure of a structure is quantified, rather than using a “factor of safety” approach. For example, it is more meaningful to say that a system has a 15 % probability of failing rather than saying the computed stress is 43 % less than the strength of the material or the system has a factor of safety of 1.75 [95–97]. Furthermore, probabilistic analyses identify those random variables that affect the probability of failure the most, thereby identifying where resources can be directed to have the most significant impact on improving either the diagnosis of risk or reducing the risk of failure directly [95–97]. Since deterministic analyses do not incorporate statistical data into the analysis, the effect of variability or uncertainty cannot be quantified. For example, the probability of failure of a structure depends not only on the mean value of the material properties, structural geometry, and environmental variables, but also on their variance and type of distribution these variables follow. In a simple stress-strength performance function, when the variance of the strength of the material is reduced, a deterministic analysis will result in an unchanged failure prediction whereas a probabilistic analysis quantifies the resulting decrease in probability of failure [95–97].
7.8 Bone Damage and Its Effects
Bone damage is known to accumulate as a normal process in living bone [98]. It is believed that the small amounts of normally occurring damage are repaired by ordinary bone turnover processes. However, if left un-repaired, or if accumulation outpaces the normal repair process, bone damage can lead to fatigue failures at stresses below the monotonic yield or failure strength during highly strenuous activities such as running or marching [99, 100]. Laboratory experiments, both in vitro and in vivo, have demonstrated that microdamage is produced by cyclic loading at physiological levels of stress or strain [101, 102].
The actual effects of damage accumulation on the mechanical properties of bone are fairly complex. Fatigue loading has been associated with modulus degradation [98], and a decrease in fracture toughness [100, 103]. When damage is accumulated in compression and the bone is tested in tension, the impact strength is reduced by an average of 40 %, although damage in tension does not reduce the impact strength in compression [104]. It was found that damage induced in machined cortical bone in tension, compression or torsion produced varying levels of stiffness change in all three loading modes [105]. The results of these initial experiments suggest that the variable effects are consistent with the microstructure of the cortical bone.
In addition to damage accumulation due to fatigue loading, damage accumulation in bone is associated with post-yield loading. It has been have postulated that inelastic behavior is primarily associated with damage accumulation, and that both inelastic strain accumulation and viscous property changes reflect the formation of new internal surfaces and voids [106–109]. There is some evidence that damage associated with inelastic strains (creep or low cycle fatigue damage) and damage associated with sub-yield strains (high cycle fatigue) are different mechanisms [110]. However, no physical basis for such a distinction has yet been identified.
Recent results suggest that the inelastic behavior and the failure of cancellous bone involve damage accumulation processes [63, 111, 112]. In cortical bone, which has been studied much more extensively than cancellous bone, the damage accumulation rate is an extremely nonlinear function of stress amplitude. In simple loading such as tension, compression or torsion, it obeys a power law relationship with stress amplitude of the form R = Aσ n , where R is a measure of damage accumulation, A is a proportionality parameter which is usually dependent on accumulated damage level, and n is a constant typically greater than 10 [109, 110]. Sufficient work has been done with cancellous bone to establish that damage is also an inherent process in cancellous bone [111, 113] and gives evidence of a similar nonlinear rate of damage accumulation [114, 115].
7.9 Continuum Damage Mechanics Modeling of Bone
Continuum damage mechanics (CDM) models, particularly when incorporated into FEA models, offer the potential for characterizing the damage accumulation process and the risk of fracture in real skeletal structures. This approach is exemplified by the work of Zysset and co-workers [115], who implemented a quite general damage model in application to cancellous bone. This work can potentially accommodate all the major features that have seen in bone behavior including plastic or viscoplastic flow and damage accumulation. Damage accumulation is incorporated around the central assumption that plastic flow and damage accumulation are intrinsically related. Zysset and Curnier incorporated this material model into a three-dimensional continuum model of anisotropic trabecular bone. Although the general model they proposed had the capability to include greater complexity, they applied the model using an assumption of isotropic damage and time independent plastic flow.
Based on evidence from our own studies [116] and others that time-dependence [117] and damage anisotropy are significant in trabecular bone and a lack of specific experimental basis for assuming an intrinsic link between plastic flow and damage, we developed a unified constitutive model to describe the elastic and inelastic (viscoelastic, plastic, and damage) behavior of human vertebral trabecular bone [116]. Material parameters were defined in terms of measures of trabecular density and architecture. Reasonable predictions of experimental specimen behavior were obtained and the ability to predict damage measures, such as evolving and accumulated modulus degradation, was achieved despite the complicated nature of the material model and limited amount of data for multiaxial material characterization. FEA simulations of specimen-level experiments support the basic assumptions of the model and demonstrated that it is possible to obtain estimates of all model parameters based on experimental data and the literature. This constitutive model was also used to investigate the effects of uniform or focal mass loss on the behavior of finite element models of idealized vertebrae, demonstrating that reduction in bone mineral density leads to an increase in the effect of accumulated damage, especially for focal loss.
7.10 Probabilistic Continuum Damage Modeling of Cortical Bone
7.10.1 Uniaxial Material Modeling
To investigate the applicability of using probabilistic methods in combination with CDM material models to predict bone failure, an initial probabilistic damage model for cortical bone was developed based on isotropic elasto-visco-plastic damage continuum mechanics (CDM) model [118]. Primary model features include the following: (a) Inelastic strains are assumed to result from either plastic flow or damage accumulation. The onset of damage accumulation and plastic flow is governed by two independent threshold surfaces in stress space. The yield criterion and the damage threshold are described by closed, convex surfaces in stress space, both of which can change by a linear hardening rule. Plastic hardening incorporates both isotropic and kinematic hardening. (b) Damage is defined by two scalar damage variables, one associated with the shear stresses and the other associated with a volumetric damage that only accumulates under positive (tensile) volumetric stress. The model incorporates nine material constants including two elastic moduli, three plasticity parameters, three damage parameters, and a time constant. A uniaxial version of the model was implemented in MATLAB for simulating axial loading. An extensive series of simulations were carried out to investigate the roles of the material parameters vis-à-vis known general behavior of bone (from experimental uniaxial test data). Parameter fits from these simulations were used to generate random variable descriptions of the CDM material model internal variables. Probabilistic calculations were then performed using the general-purpose probabilistic analysis software NESSUS (NESSUS v.7.5 Southwest Research Institute, San Antonio, TX).
The initial analysis investigated the probabilistic behavior of the model when driven to a specific strain level by computing the probability of bone failure at that strain level. Probability of bone failure was defined as the probability of reaching a specific reduction in modulus (resulting from the damage process). Modulus reduction at failure for each experimental data set was computed and used as a random variable describing strength. The performance function for this analysis was defined as g = R−S where R is the strength random variable (modulus reduction limit at failure) and S is the model computed response (computed reduction in modulus). The probability of failure is defined as p[g ≤0].
The parameter estimation produced a set of material model random variables that best described the behavior of the material under uniaxial loading. The average reduction in modulus compiled from the curve fits to the experimental results was 52 % (±18 %) The predicted probability of failure for a set of give strain levels is given in Fig. 7.4 as a function of strain rate. At a strain level of 1.5 %, the probabilistic model predicts a probability of bone failure of 62 % for the slowest strain rate to 98 % for the highest strain rate. Slower strain rate simulations resulted in lower probabilities of failure for a given strain level. The uniaxial implementation of the CDM model accurately predicts the experimental behavior of cortical bone uniaxially loaded to failure in tension. Furthermore, using a probabilistic modeling approach, this type of material model can be used to predict the probability of failure given a set of uncertain material model parameters and boundary conditions.
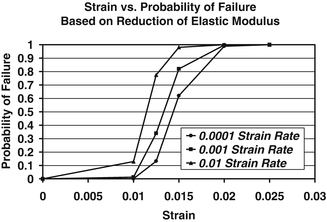

Fig. 7.4
Probability of bone failure at a given strain level. Failure is based on accumulated damage (modulus reduction)
7.10.2 Probabilistic Analysis of Cortical Bone Failure using FEA
To further investigate the utility of probabilistic methods combined with continuum damage mechanics models of bone behavior to predict bone failure, we recently modeled the tensile uniaxial load to failure behavior of cortical bone an existing elastic, viscoplastic, CDM material model available in the commercial finite element analysis code LS-DYNA (LS-DYNA v.960, LSTC, Livermore CA). This CDM model differed from the one described above in that, since it was developed to model the behavior of metals, it does not include viscoelastic effects. Furthermore, damage is dependent upon plastic strain. A non-linear optimization procedure was implemented to determine the material parameters such the computed stress–strain behavior agreed with the experimental behavior (Fig. 7.5). This procedure was performed independently using archival data from five specimens [119] resulting in five sets of material parameters. Random variable descriptions of each material model parameter were determined from this set of material parameters and a probabilistic analysis simulating the uniaxial tensile loading was performed using the maximum stress attained during the simulation as the performance function. Thus, the result of probabilistic analysis is a predicted cumulative distribution function (CDF) of the maximum stress attained during a uniaxial tension test to failure. To quantify the predictive accuracy of the probabilistic analysis, the CDF of maximum attained stress compiled from the results of 60 independent cortical bone tension tests, in which each specimen was loaded to failure, was constructed and compared to the predicted CDF from the probabilistic analysis (Fig. 7.6). The CDF of the experimental data quantifies the variability associated with the tensile behavior of cortical bone.
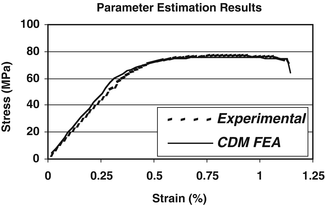
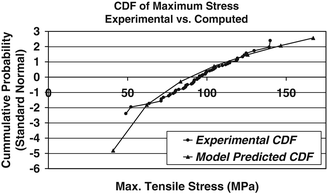

Fig. 7.5
CDM material model parameter estimation results. The results from fits of five independent tensile tests were used to determine the random variable descriptions of each material model parameter

Fig. 7.6
Experimental versus predicted CDF of the maximum stress attained during a probabilistically simulated tensile test of cortical bone
Good agreement is shown between the predicted CDF and CDF based on the measured experimental data. Based on a Kolmogorov-Smirnov goodness of fit test, there is no statistical difference between the experimental data CDF and the computationally predicted CDF. The probabilistic model slightly under predicts the mean value and over predicts the standard deviation of the maximum tensile stress.
A deterministic analysis would only predict the mean value of the maximum stress giving no indication of the variability that can be expected. In contrast, the probabilistic analysis not only accurately predicts the mean value it also accurately predicts the variation in the response. A deterministic analysis can only provide a binary answer when assessing a structure: either the stress is less than the strength in which case the structure does not fail, or the stress is equal to or greater than the strength wherein the structure will fail. A probabilistic analysis, alternatively, will quantify the probability that a stress will be greater than the material strength. Thus, this straightforward application demonstrates the ability of probabilistic analysis methods to successfully model uncertainty and variability in the tensile behavior of cortical bone.
7.10.3 Probabilistic Analysis of Trabecular Bone Damaging Behavior
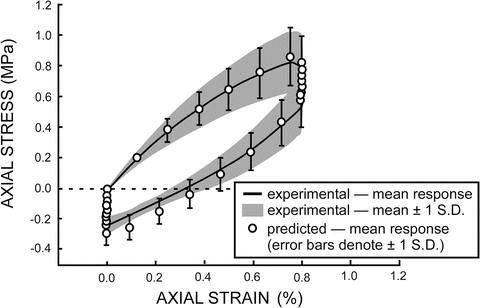
In order to investigate variability in the evolving response of human vertebral trabecular bone, material model parameters were estimated individually for 10 experimental specimens using genetic algorithm based optimization combined with a phenomenological constitutive model (above and [120, 121]). The constitutive model and resulting material parameter distributions were implemented using MATLAB within a probabilistic analysis framework (NESSUS, SwRI) and the mean and variation of the experimental specimen response were successfully determined (Fig. 7.7).