2
Biomechanics of Synovial Joints
THAY Q. LEE, STEFAN FORNALSKI, TOMOYUJI SASAKI, AND SAVIO L.-Y. WOO
Human movement is possible due to the unique design and function of the synovial joint. Whether it is activities of daily living such as walking or high-performance activity in a sporting event, the synovial joint depends on complex interactions that occur between connective tissue structures. These structures include ligaments, tendons, menisci, subchondral bone, fibrous capsule, synovium, and hyaline articular cartilage. Articular cartilage is an integral component in this nearly frictionless system.
Articular cartilage functions under high loads with good tissue integrity into the seventh or eighth decade of life. This is due to the unique structural and biomechanical properties of articular cartilage. The intricate biomechanical behavior of articular cartilage is the result of its multiphasic material property, consisting of both a liquid and solid phase, unique viscoelastic properties, and swelling properties.1 Articular cartilage and synovial joint lubrication allows a large range of joint loading conditions throughout life with minimal cartilage wear. Cartilage injury may occur over time as seen in chronic degenerative osteoarthritis or from acute athletic injuries. Athletic cartilage injuries may occur from acute direct trauma with excessive joint loading or from chronic altered joint biomechanics as observed in the sequelae of anterior cruciate ligament injuries.2 In the elderly, failed nonsurgical management of osteoarthritis is addressed with joint replacement such as total hip or total knee arthroplasty. In the younger, active, athletic patient, joint arthroplasty is not the first line of surgical management. Some of the surgical treatments for the younger athletic patient include arthroscopic joint debridement, abrasion arthroplasty, subchondral drilling, osteochondral allografts, autologous chondrocyte implantation, and autologous osteochondral transplantation.3
This chapter discusses basic biomechanics, the composition and biomechanics of synovial joints with a focus on articular cartilage and joint lubrication, the effects of joint loading and altered biomechanics on articular cartilage, and the biomechanics of current cartilage repair including the surgical procedures of autologous chondrocyte implantation and autologous osteochondral transplantation.
 Biomechanics
Biomechanics
Newton’s Laws
Newton’s first law states that if a zero net external force is applied to a body, that body will remain in constant motion or at rest (sum of external forces applied to body equals zero). Newton’s second law states that the acceleration of an object with a mass is directly proportional to the force applied to the object. Newton’s third law states that for every action there is an equal and opposite reaction.4 Biomechanics applies Newton’s laws of motion to biologic systems to describe the function as well as the mechanical and structural integrity of the system.
Forces, including joint reaction force, are important parameters in understanding joint stability and function. Forces are vector quantities, which have both direction and magnitude. The length of the vector equals magnitude, the tail of the vector is the point of force application, the head of the vector is the direction, and the orientation of the vector is the line of action. Force, velocity, acceleration, and moment are also vector quantities. When a person is standing, a force exists between the foot and floor according to Newtons’s third law (action with opposite reaction).5 The joint forces usually considered are compression and tension in a perpendicular orientation to the articular surface and shear force in a parallel orientation to the articular surface. The principle of the “parallelogram of forces” allows vectors to be added, producing a resultant vector. By the same principle, vectors can also be broken down into component forces such as compression and shear force, which exist in different planes.
Moment is the rotational effect of a force on a body about an axis. A force acting at a distance from an axis produces a moment or torque about the point. For example, the biceps muscle acts at a defined perpendicular distance from the center of elbow rotation. Moment equals the force multiplied by the perpendicular distance to a specified axis of rotation (moment arm). An important concept for understanding muscle forces around joints is the force couple. A couple is a moment created by equal, parallel, but opposite directed forces. The force created by the couple is zero at equilibrium.1,5
Statics
Statics is the study of the action of forces on a joint or body at rest or in equilibrium. Although most biologic systems are normally not in complete equilibrium, the concept of static equilibrium is helpful in determining unknown forces or moments about synovial joints. Assumptions made with this model are that the bodies are completely rigid and that the sum of all forces and moments equal zero.1,5,6 Free body diagrams use the concept of equilibrium and the known forces and moments to solve for unknown forces and moments.
Dynamics
Dynamics is the study of nonequilibrium conditions. An unopposed force acting on a body changes the velocity of the object. This may mean a change in direction or acceleration or deceleration. Acceleration produced by a linear force is termed linear acceleration and that about an axis of rotation with torque is termed angular acceleration. An example of linear deceleration is a basketball player landing from a jump. The downward velocity is being acted upon by the upward ground reaction force. This linear deceleration is proportional to the ground reaction force. By decreasing the deceleration by bending the knees and wearing shock-absorbing tennis shoes, the person can decrease the impact or ground reaction force.1,5 An example of angular acceleration is a baseball pitcher throwing from the late cocking phase to the release phase of throwing.
Kinematics
Kinematics is the study of joint or body motion in terms of displacement, acceleration, and velocity without consideration of forces or moments on the moving body. Range of motion in a joint is constrained by the shape of the articulation (e.g., ball-and-socket or hinge joint), overall osseous architecture, active muscle forces, and by passive soft tissue constraints. To describe joint motion, a reference frame must be assumed. In a three-dimensional coordinate system of x, y, and z axes, the joint motion of translation and rotation occurs in six degrees of freedom. In a two-dimensional reference frame, only two coordinates (i.e., x and y) are required to define the position vector. In three dimensions a total of three coordinates (i.e., x, y, and z) and three orientation angles relative to the reference frame are required to define the position vector.1,5,6
Velocity vectors are defined as the change in displacement with respect to time. Synovial joint motion consists of both translational (sliding) and rolling motion. The amount of translation and rolling motion varies from joint to joint. If two points on a rigid body are moving in the same direction, pure translation is occurring. If two points are moving in different directions, both translation and rotation are occurring.1,5
The instant center of rotation is the point at which the joint rotates. In the knee, the instant center of rotation changes due to the added translation of the joint. The instant center of rotation normally lies on a line perpendicular to the tangent of the joint surface at all contact points. Pure translation has no angular changes and as such no instant center of rotation.1,5,6
 Structural Properties
Structural Properties
When an object is subjected to an external load, it will give a deformation response that is dependent on the magnitude and direction of the applied load, the materials that make up the object, and the shape and size of the object. The load-deformation curve is similar to the stress-strain curve and is derived by plotting the force applied by the deformation produced. The load-deformation curve relates to the structural properties of materials, that is, it is being affected by the size, shape, and intrinsic material properties. The slope in the linear elastic region of the load-deformation curve is referred to as the stiffness of the structure (Fig. 2–1).
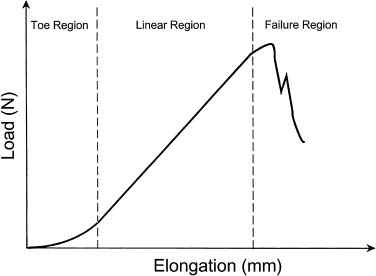
FIGURE 2–1 Load-elongation curve for tendon showing distinct response regions.1
Material Properties
Stress-strain curves relate to material properties. Stress is a physical quantity defined as force per unit area. This concept can be applied to an elderly patient with osteoarthritis. In degenerative joint disease, joint surface congruity is decreased, producing decreased contact area, increased stress on articular cartilage, and in turn the predisposition for degenerative changes. Compressive and tensile stresses refer to the stresses that are perpendicular to the surface, whereas shear stress refers to the stresses that are parallel to the surface. Strain is a relative measure of deformation. It is equal to the change in length of an object divided by the original length of the object. A stress-strain curve is simply the relationship of stress versus strain. In the elastic region of the curve (linear portion) the stress and strain are directly proportional and the elastic deformation is fully recoverable (strain is completely recovered on stress removal). This linear region, calculated as a slope, is known as Young’s modulus of elasticity and represents the ability of a material to resist deformation.1,5 The proportional limit (P) refers to a point at the end of the elastic range where stress-strain is no longer proportional. Past this point a small amount of plastic deformation occurs, and when the force is released a small permanent deformation exists (all of strain is not recovered) due to damage of the internal structure of the tissue. The yield strength (Y) is the point at which a nonrecoverable strain starts to occur, typically 0.2% strain past the proportional limit. Ultimate tensile strength (U) is the point of specimen failure. Stress at failure is usually thought of as the strength of the material. The area beneath the stress-strain curve is the intrinsic material toughness. The stress-strain curves can typically be used to characterize the intrinsic material properties.
Linear elasticity has three important fundamental principles: (1) stress and strain are directly proportional, (2) strain produced is reversible once stress is removed, (3) the material response is insensitive to the rate of loading.1,5,6 In living connective tissue, linear elasticity does not represent a true model, and the property of viscoelasticity must be recognized.
Viscoelasticity
In musculoskeletal tissue, linear elastic behavior is not frequently observed. Muscles, tendons, ligaments, cartilage, and bone exhibit the property of viscoelasticity.1,5–7 Viscoelastic behavior is time dependent and is the manifestation of the internal friction within a biologic material. The stress-strain relationship is dependent on the strain rate, where the force response increases with the increasing rate of deformation.
Viscoelastic materials exhibit the unique behavior of creep and stress relaxation.7,8 Creep is seen when a constant force is applied to a material causing increasing deformation until an equilibrium state is reached. Stress-relaxation is seen with a constantly held deformation, where force decreases over time until some equilibrium is reached.1,5–8 Synovial joints display the viscoelastic properties of creep and stress relaxation.
Isotropy/Anisotropy
Biologic materials also have directional properties termed isotropy and anisotropy. Isotropic materials have intrinsic material properties independent of the direction of loading. Such materials include cancellous bone, plastic, and metals. Isotropic materials have a random internal structure. In contrast, anisotropic materials have intrinsic material properties that are dependent on the result of the direction of loading. An example of this is the trabecular pattern seen in the proximal femur. Anisotropic materials include bone, meniscus, ligaments, tendon, and articular cartilage. Anisotropic materials usually have an organized internal structure.1,5
 Synovial Joints
Synovial Joints
Joint Composition
The proper function of a synovial joint, such as the knee, requires intricate function and coordination of multiple connective tissues. Synovial joint connective tissue structures include ligaments, tendons, meniscus, subchondral bone, the fibrous capsule, synovium, and articular cartilage. Both intraarticular and extraarticular ligaments are important for providing physical restraints, for both joint stability and limiting joint range of motion. Tendons provide a mechanism for transfer of muscle forces to bony insertions and across synovial joints to produce movement. The meniscus functions in force dispersion and in creating an improved functional congruity within a joint. The fibrous capsule and synovial lining constitute the boundaries of the synovial joint and are bathed in synovial fluid. Hyaline articular cartilage lines the subchondral bone of synovial joints, and functions to provide a lubricated and nearly frictionless weight-bearing surface, to protect subchondral bone, and to more evenly distribute forces to subchondral bone.9 Articular cartilage functions under high loads with good tissue integrity into the seventh and eighth decade of life. The following sections discuss the unique composition of articular cartilage, the biomechanics of articular cartilage, and synovium/lubrication theories.
Articular Cartilage Composition
Articular cartilage lines the load-bearing surfaces in synovial joints. Through its unique biomechanical and structural properties, it functions to minimize friction between articulating surfaces, to absorb mechanical loads, and to spread joint loads over larger surface areas and to subchondral bone. Articular cartilage is avascular, aneural, and alymphatic, and it receives nutrients through diffusion in synovial fluid. In turn, cartilage shows poor healing capacity. Both the unique structural and biomechanical properties of articular cartilage allow synovial joints to function in a variety of loading conditions throughout life.1
Structurally cartilage is composed of a large extracellular matrix (ECM) interspersed with specialized cartilage cells called the chondrocytes. The components of the ECM primarily include water (60–80%), collagen type II (10–20%), proteoglycans (4–7%), and other proteins and glycoproteins (<5%). Collagen and proteoglycans are the two major structural macromolecules in the articular cartilage ECM.1,5,10,11
Water
Water makes up about 60 to 80% of the wet weight of articular cartilage. This includes intracellular (chondrocytes) water, although the majority of water in articular cartilage is in the molecular pores of the ECM. Dissolved in water are sodium, calcium, potassium, and chloride. The relative water concentration decreases from the superficial to deeper zones in articular cartilage.10,11 Water moves through the ECM by mechanical compression of the ECM and also due to a pressure gradient. The permeability of articular cartilage is low. As water moves through the molecular pores in the ECM, high frictional resistance is encountered. Pressurization within the ECM, with mechanical loading and frictional resistance of water movement, are critical to articular cartilage biomechanics and its load-bearing capacity. Water flow is also important for nutrient flow within the tissue. In addition, as described in the lubrication section, water is important in the weeping effect of lubrication.12–14 An important quality of articular cartilage is its hydrophilic nature. This is mostly due to the proteoglycans. The interaction among water, proteoglycans, and collagen is critical in forming a solid resilient cartilage matrix.11,15
Chondrocytes
Chondrocytes are specialized cartilage cells derived from mesenchymal cells. They occupy less than 10% of the cartilage volume. Chondrocytes maintain the ECM and produce collagen, proteoglycans, and glycoproteins. These cells respond to growth factors, interleukins, medications, and physical stimulation such as mechanical and hydrostatic pressure changes.5,16,17
Collagens
The major structural component of the ECM is the collagen macromolecule. There are numerous types of collagen in bone, tendon, skin, blood vessels, ligaments, and cartilage. Characteristically collagen consists of a triple-helical structure composed of three polypeptide chains (α chains) (Fig. 2–2).1,16 In articular cartilage, over 50% of the dry weight is collagen. Type II collagen is the predominant (95%) collagen in articular cartilage. Other types in articular cartilage include types V, VI, IX, X, and XI.1,10,15,16 Collagen provides the shear and tensile properties of articular cartilage and also anchors proteoglycans within the ECM. Other collagen functions include type VI in anchoring chondrocytes in the matrix, type X in mineralization in the deeper cartilage layers, and types IX and XI may function to form cross-links between type II collagen fibers.5 Collagen cross-linking increases the insolubility of collagen in the ECM and likely is involved with the tensile properties of articular cartilage.1,6,17
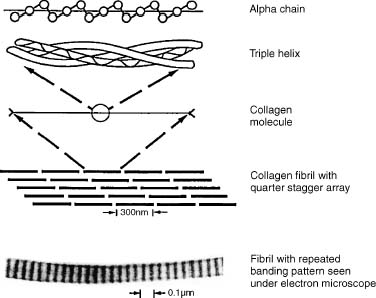
FIGURE 2–2 Illustration showing hierarchical organization and photomicrograph of collagen fibril.1
Proteoglycans
Proteoglycans are large ECM molecules composed of a protein core and covalently bound glycosaminoglycan (GAG) chains. Proteoglycans are hydrophilic, producing the water affinity of articular cartilage.1,14,15 GAGs are long unbranched disaccharide units. The three types most often found in articular cartilage are keratan sulfate, dermatan sulfate, and chondroitin 4- and 6-sulfate. The chondroitin sulfates are the most prevalent and account for over 50% of the GAG.5 GAG chains have repeating sulfate (SO4) and/or carboxyl (COOH) groups that become ionized in solution and in the physiologic environment. These negative charges require positive counter-ions such as calcium and sodium ions (positive ions in solution). These free ions give rise to an osmotic pressure also known as the Donnan effect. In addition, the negative GAG charges result in charge-to-charge repulsive forces. As will be described in later sections both the osmotic pressure and charged repulsive forces are important for maintaining the structural integrity of articular cartilage.5,10,11,14,15
The majority of proteoglycans in articular cartilage are of the aggrecan type. These are composed of a long protein core molecule with up to 100 GAGs covalently bound to the protein core (Fig. 2–3).1,5 Hyaluronate is an unusual GAG that is very large in size, not bound to a protein core, and without sulfate groups. Hyaluronate and numerous aggrecan molecules binding to hyaluronate form large macromolecular complexes similar in structure to that of a bottle brush (Fig. 2–4).1 This large macromolecular size likely aids in stabilizing the aggrecan molecules in the ECM.1,10,11,16 Smaller proteoglycan molecules in articular cartilage include decorin, biglycan, and fibromodulin. The role of these smaller molecules is not as well understood as that of the aggrecan type.1
Structural Matrix
The macromolecular organization of the proteoglycan-collagen and the proteoglycan-proteoglycan interaction and water content within the ECM combine to produce a solid and rigid matrix.1,10 The large proteoglycans trapped within the ECM attract water, creating a swelling pressure. This swelling pressure expands and is countered in force by the cross-linked collagen network (Fig. 2–5). To simplify the discussion, collagen and proteoglycan interact to form a porous resilient matrix and trap water molecules to give cartilage its unique swelling properties. This unique structural organization creates the dynamic biomechanical properties seen in articular cartilage.1,10,11,15
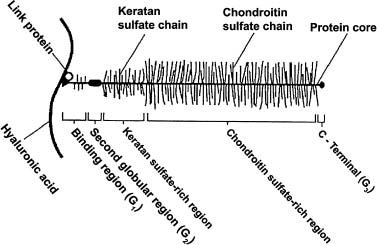
FIGURE 2–3
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


