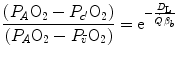–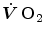 Diagram
Diagram
Abstract
This chapter contains an analysis of the steady-state concept, as it is applied during light exercise. In this case, oxygen consumption increases upon exercise onset to attain a steady level, which can be maintained for a long period of time. The steady-state oxygen consumption is proportional to the exerted mechanical power. Under these circumstances, there is neither accumulation of lactate in blood nor changes in muscle phosphocreatine concentration: aerobic metabolism sustains the entire energy requirement of the exercising body. Once the steady state has been attained, the flow of oxygen is the same at all levels along the respiratory system. The quantitative relations determining the flow of oxygen across the alveoli and in blood are discussed. Special attention is given to the effects of ventilation—perfusion inequality and to the diffusion—perfusion interaction equations. The cardiovascular responses at exercise steady state are analysed in the context of the equilibrium between systemic oxygen delivery and systemic oxygen return. The relationship between oxygen consumption and power is discussed, along with the distinction between external and internal work during cycling. The concepts of mechanical efficiency of exercise and energy cost of locomotion are analysed. Concerning the latter, the distinction between aerodynamic work and frictional work is introduced. The roles of the cross-sectional surface area on the frontal plane and of air density in aerodynamic work are discussed. To end with, an equation linking ventilation, circulation and metabolism at exercise in a tight manner is developed, around the notion that the homeostasis of the respiratory system at exercise is maintained around given values of the constant oxygen return. This equation tells that, as long as we are during steady-state exercise in normoxia, any increase in the exercise metabolic rate requires an increase in ventilation that is proportional to that in oxygen consumption only if the pulmonary respiratory quotient stays invariant does not change, and an increase in cardiac output that is not proportional to the corresponding increase in oxygen consumption. At intense exercise, when lactate accumulation also occurs and hyperventilation superimposes, a new steady state would be attained only at 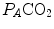 values lower than 40 mmHg: the homeostasis of the respiratory system would be modified. This new steady state, however, is never attained in fact, for reasons that are discussed in Chap. 3.
values lower than 40 mmHg: the homeostasis of the respiratory system would be modified. This new steady state, however, is never attained in fact, for reasons that are discussed in Chap. 3.
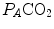 values lower than 40 mmHg: the homeostasis of the respiratory system would be modified. This new steady state, however, is never attained in fact, for reasons that are discussed in Chap. 3.
values lower than 40 mmHg: the homeostasis of the respiratory system would be modified. This new steady state, however, is never attained in fact, for reasons that are discussed in Chap. 3.Introduction
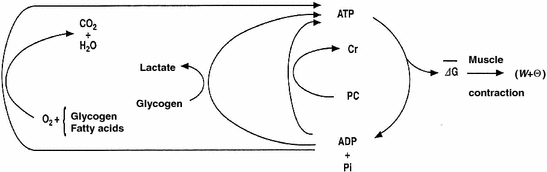
The general theory of the energetics of muscular exercise looks at muscle as a biological engine, in which chemical energy—or metabolic energy—is transformed in mechanical work and heat. The ultimate step of this energy transformation is provided by ATP hydrolysis in the cross-bridge cycle. The low ATP concentration in muscle (on average 5 mmol per kg of wet muscle) requires continuous ATP resynthesis, which we owe to the ensemble of reactions comprised in the concept of intermediate metabolism. The detailed description of these reactions can be found in biochemistry textbooks, and the historical developments that led to them are summarized in Chap. 1. The general theory summarizes these reactions in three basic physiological concepts: aerobic metabolism, anaerobic lactic metabolism and anaerobic alactic metabolism. Aerobic metabolism includes the oxidation of glycogen and fatty acids to pyruvate and acetate, respectively, and their introduction into the Krebs cycle which feeds oxidative phosphorylation. It uses oxygen as oxidizer and has carbon dioxide as end product. Anaerobic lactic metabolism concerns the degradation of glycogen to pyruvate, with subsequent transformation in lactate. It occurs when the rate of energy transformation in the glycolytic pathway exceeds that of further oxidation of pyruvate in the Krebs cycle. Anaerobic alactic metabolism consists of the Lohmann’s reaction. A qualitative representation of these concepts is shown in Fig. 2.1. A practical consequence of this picture of metabolism is that the rate at which metabolic energy is transformed by aerobic metabolism can be determined by a simple measure of oxygen consumption 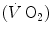 . Similarly, the rate of lactate accumulation in blood (
. Similarly, the rate of lactate accumulation in blood (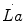 ) is a measure of the rate of anaerobic lactic metabolism, and the rate at which phosphocreatine concentration varies in muscle (
) is a measure of the rate of anaerobic lactic metabolism, and the rate at which phosphocreatine concentration varies in muscle (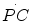 ) defines the rate of anaerobic alactic metabolism.
) defines the rate of anaerobic alactic metabolism.
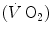 . Similarly, the rate of lactate accumulation in blood (
. Similarly, the rate of lactate accumulation in blood (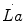 ) is a measure of the rate of anaerobic lactic metabolism, and the rate at which phosphocreatine concentration varies in muscle (
) is a measure of the rate of anaerobic lactic metabolism, and the rate at which phosphocreatine concentration varies in muscle (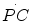 ) defines the rate of anaerobic alactic metabolism.
) defines the rate of anaerobic alactic metabolism.
Fig. 2.1
Schematic representation of the energetics of muscular exercise. ATP hydrolysis liberates the free energy (∆G) that contractile proteins use to generate work (W) and heat (Θ). ATP resynthesis takes place through the indicated pathways. ADP adenosine di-phosphate; Pi inorganic phosphate; PC phosphocreatine; Cr creatine. Modified after di Prampero (1985)
The quantitative representation of the same concepts takes the following algebraic form:
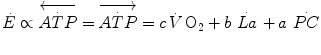
where 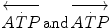 are the rates of ATP hydrolysis and resynthesis, respectively. Equation (2.1) can be defined as the general equation of the energetics of muscular exercise. In this equation,
are the rates of ATP hydrolysis and resynthesis, respectively. Equation (2.1) can be defined as the general equation of the energetics of muscular exercise. In this equation, 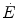 is the overall rate of metabolic energy liberation, whereas the three constants a, b and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolysed, a mole of lactate accumulated, and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1; c (otherwise P/O2 ratio) takes a mean value of 6.17 for glycogen oxidation into glycolysis. For constant b, the situation is a bit more complex than this (di Prampero 1981; di Prampero and Ferretti 1999) and will be discussed in Chap. 6.
is the overall rate of metabolic energy liberation, whereas the three constants a, b and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolysed, a mole of lactate accumulated, and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1; c (otherwise P/O2 ratio) takes a mean value of 6.17 for glycogen oxidation into glycolysis. For constant b, the situation is a bit more complex than this (di Prampero 1981; di Prampero and Ferretti 1999) and will be discussed in Chap. 6.
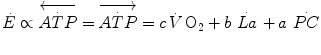
(2.1)
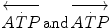 are the rates of ATP hydrolysis and resynthesis, respectively. Equation (2.1) can be defined as the general equation of the energetics of muscular exercise. In this equation,
are the rates of ATP hydrolysis and resynthesis, respectively. Equation (2.1) can be defined as the general equation of the energetics of muscular exercise. In this equation, 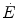 is the overall rate of metabolic energy liberation, whereas the three constants a, b and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolysed, a mole of lactate accumulated, and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1; c (otherwise P/O2 ratio) takes a mean value of 6.17 for glycogen oxidation into glycolysis. For constant b, the situation is a bit more complex than this (di Prampero 1981; di Prampero and Ferretti 1999) and will be discussed in Chap. 6.
is the overall rate of metabolic energy liberation, whereas the three constants a, b and c are proportionality constants indicating the moles of ATP resynthesized, respectively, by a mole of phosphocreatine hydrolysed, a mole of lactate accumulated, and a mole of oxygen consumed. The Lohmann’s reaction tells that a is equal to 1; c (otherwise P/O2 ratio) takes a mean value of 6.17 for glycogen oxidation into glycolysis. For constant b, the situation is a bit more complex than this (di Prampero 1981; di Prampero and Ferretti 1999) and will be discussed in Chap. 6.In humans at rest and during light exercise, 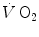 attains a steady level which can be maintained for a long period of time. Under these steady-state conditions, there is neither accumulation of lactate in blood nor changes in muscle phosphocreatine concentration. Thus, Eq. (2.1) reduces to the following:
attains a steady level which can be maintained for a long period of time. Under these steady-state conditions, there is neither accumulation of lactate in blood nor changes in muscle phosphocreatine concentration. Thus, Eq. (2.1) reduces to the following:
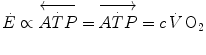
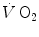 attains a steady level which can be maintained for a long period of time. Under these steady-state conditions, there is neither accumulation of lactate in blood nor changes in muscle phosphocreatine concentration. Thus, Eq. (2.1) reduces to the following:
attains a steady level which can be maintained for a long period of time. Under these steady-state conditions, there is neither accumulation of lactate in blood nor changes in muscle phosphocreatine concentration. Thus, Eq. (2.1) reduces to the following: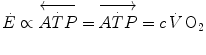
(2.2)
Equation (2.2) indicates that all energy-sustaining body functions at rest plus the mechanical work of exercise derives from aerobic energy sources. This represents a particularly favourable condition for exercise physiologists, because a simple measure of 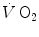 at the mouth informs on the overall metabolic power, which remains invariant in time.
at the mouth informs on the overall metabolic power, which remains invariant in time.
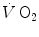 at the mouth informs on the overall metabolic power, which remains invariant in time.
at the mouth informs on the overall metabolic power, which remains invariant in time.In this chapter, I will discuss the steady-state concept and describe the quantitative relationships that characterize it. Making use of the steady-state concept, I will then introduce the concepts of energy cost of locomotion and of mechanical efficiency of exercise. Finally, I will present and discuss the cardiopulmonary responses to exercise at steady state, and I will propose a synthesis of the interrelated phenomena along the respiratory system by which a steady 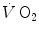 is maintained throughout the exercise.
is maintained throughout the exercise.
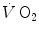 is maintained throughout the exercise.
is maintained throughout the exercise.The Steady-State Concept
The steady-state concept was clearly defined for the first time by Bock et al. (1928). According to them, a steady state implies an invariant 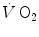 , a steady rate of elimination of carbon dioxide
, a steady rate of elimination of carbon dioxide 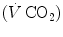 produced by metabolism only, steady heart rate (f h ) and an essentially stable internal environment. If this is so, then (i) the
produced by metabolism only, steady heart rate (f h ) and an essentially stable internal environment. If this is so, then (i) the 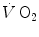 measured at the mouth corresponds to the rate of oxygen consumption by the mitochondria; (ii) both
measured at the mouth corresponds to the rate of oxygen consumption by the mitochondria; (ii) both 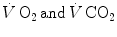 are characterized by equal values at any level along the respiratory system; (iii) as a consequence, the respiratory quotient determined at the lungs (RQ L )—or gas exchange ratio, defined as the ratio between
are characterized by equal values at any level along the respiratory system; (iii) as a consequence, the respiratory quotient determined at the lungs (RQ L )—or gas exchange ratio, defined as the ratio between 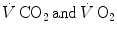 —is equal at any level along the respiratory system, so that it corresponds exactly to the metabolic respiratory quotient (RQ M ), that is, the ratio between the moles of carbon dioxide produced and the moles of oxygen consumed in the cellular aerobic energy transformation processes. Starting from these bases, taken as axioms, several developments in the analysis of the quantitative relationships describing gas flows in the respiratory system at rest and exercise were pursued.
—is equal at any level along the respiratory system, so that it corresponds exactly to the metabolic respiratory quotient (RQ M ), that is, the ratio between the moles of carbon dioxide produced and the moles of oxygen consumed in the cellular aerobic energy transformation processes. Starting from these bases, taken as axioms, several developments in the analysis of the quantitative relationships describing gas flows in the respiratory system at rest and exercise were pursued.
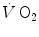 , a steady rate of elimination of carbon dioxide
, a steady rate of elimination of carbon dioxide 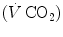 produced by metabolism only, steady heart rate (f h ) and an essentially stable internal environment. If this is so, then (i) the
produced by metabolism only, steady heart rate (f h ) and an essentially stable internal environment. If this is so, then (i) the 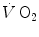 measured at the mouth corresponds to the rate of oxygen consumption by the mitochondria; (ii) both
measured at the mouth corresponds to the rate of oxygen consumption by the mitochondria; (ii) both 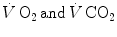 are characterized by equal values at any level along the respiratory system; (iii) as a consequence, the respiratory quotient determined at the lungs (RQ L )—or gas exchange ratio, defined as the ratio between
are characterized by equal values at any level along the respiratory system; (iii) as a consequence, the respiratory quotient determined at the lungs (RQ L )—or gas exchange ratio, defined as the ratio between 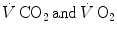 —is equal at any level along the respiratory system, so that it corresponds exactly to the metabolic respiratory quotient (RQ M ), that is, the ratio between the moles of carbon dioxide produced and the moles of oxygen consumed in the cellular aerobic energy transformation processes. Starting from these bases, taken as axioms, several developments in the analysis of the quantitative relationships describing gas flows in the respiratory system at rest and exercise were pursued.
—is equal at any level along the respiratory system, so that it corresponds exactly to the metabolic respiratory quotient (RQ M ), that is, the ratio between the moles of carbon dioxide produced and the moles of oxygen consumed in the cellular aerobic energy transformation processes. Starting from these bases, taken as axioms, several developments in the analysis of the quantitative relationships describing gas flows in the respiratory system at rest and exercise were pursued.Before entering into these details, however, it is necessary to point out that the steady-state concept is a mental creation of some bright physiologists, which represents an oversimplification of what actually occurs in a living organism. In fact, even at steady state, the respiratory system is characterized by oxygen flow discontinuities, heterogeneities and spontaneous variations, depending on the macroscopic and microscopic organization of the system itself. From the macroscopic viewpoint, note that ventilation occurs in a dead-end pathway, so that inhalation and exhalation occur necessarily in alternate manner. Moreover, the heart alternates systoles and diastoles, with associated opening and closing of heart valves. Both mechanisms are sources of discontinuities, the former in air, the latter in blood flow, both in oxygen flow. Moreover, there is a spontaneous variability of respiratory and cardiac rhythms, related to mechanical and neural control mechanisms (Cottin et al. 2008; Perini and Veicsteinas 2003). This being the case, the 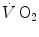 at steady state is not a continuous invariant flow: it rather corresponds to an invariant integral mean of a flow that is highly variable in time, at several levels even discontinuous.
at steady state is not a continuous invariant flow: it rather corresponds to an invariant integral mean of a flow that is highly variable in time, at several levels even discontinuous.
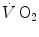 at steady state is not a continuous invariant flow: it rather corresponds to an invariant integral mean of a flow that is highly variable in time, at several levels even discontinuous.
at steady state is not a continuous invariant flow: it rather corresponds to an invariant integral mean of a flow that is highly variable in time, at several levels even discontinuous.From the microscopic viewpoint, blood flow is pulsatile in lung capillaries, because of their heterogeneous recruitment, and of interferences from the rhythmic activity of the heart and the lungs (Baumgartner et al. 2003; Clark et al. 2011; Tanabe et al. 1998). This heterogeneity may be reduced during exercise due to simultaneous recruitment of a larger number of lung capillaries. Similar heterogeneities have been demonstrated also in contracting skeletal muscles, both in space and in time (Armstrong et al. 1987; Ellis et al. 1994; Heinonen et al. 2007; Marconi et al. 1988; Piiper et al. 1985). Heterogeneous muscle blood flow was reported also in non-contracting muscles of exercising humans (Heinonen et al. 2012). Contracting muscle fibres are likely unperfused, because they generate pressure, which compresses and closes muscle capillaries from outside. If this is so, perfusion occurs only in relaxing muscle fibres, so that muscle fibre oxygenation takes place during relaxation, not during contraction. In this case, the alternate recruitment of neighbouring motor units becomes a functional necessity, the inevitable consequence of which is heterogeneity of muscle blood flow distribution during muscular work.
Quantitative Relationships at Steady State
The first relationships to be established in time concern the net amount of gas exchanged in the lungs and in blood, calculated as difference between a flow in and a flow out for the gas at stake. Concerning blood, this gave origin to what is nowadays called the Fick principle, whose algebraic expression is as follows (Fick 1870):
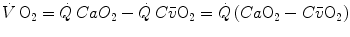
where 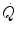 is total blood flow—or more commonly cardiac output—and
is total blood flow—or more commonly cardiac output—and 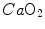 and
and 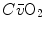 are the oxygen concentrations in arterial and mixed venous blood, respectively. This expression in fact defines the amount of oxygen that leaves the blood in peripheral capillaries to be consumed in cells in a unit of time. By analogy, Geppert and Zuntz (1888) defined
are the oxygen concentrations in arterial and mixed venous blood, respectively. This expression in fact defines the amount of oxygen that leaves the blood in peripheral capillaries to be consumed in cells in a unit of time. By analogy, Geppert and Zuntz (1888) defined 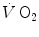 as the difference between inspired and expired oxygen flows, as follows:
as the difference between inspired and expired oxygen flows, as follows:
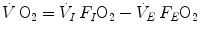
where 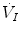 is the total inspired air flow—or more commonly inspiratory ventilation;
is the total inspired air flow—or more commonly inspiratory ventilation; 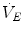 is the total expired air flow—or more commonly expiratory ventilation; and
is the total expired air flow—or more commonly expiratory ventilation; and 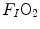 and
and 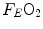 are the oxygen fractions in inspired and expired air, respectively. By definition, at steady state, Eqs. (2.3) and (2.4) have equal solutions.
are the oxygen fractions in inspired and expired air, respectively. By definition, at steady state, Eqs. (2.3) and (2.4) have equal solutions.
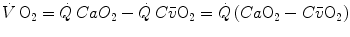
(2.3)
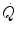 is total blood flow—or more commonly cardiac output—and
is total blood flow—or more commonly cardiac output—and 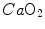 and
and 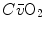 are the oxygen concentrations in arterial and mixed venous blood, respectively. This expression in fact defines the amount of oxygen that leaves the blood in peripheral capillaries to be consumed in cells in a unit of time. By analogy, Geppert and Zuntz (1888) defined
are the oxygen concentrations in arterial and mixed venous blood, respectively. This expression in fact defines the amount of oxygen that leaves the blood in peripheral capillaries to be consumed in cells in a unit of time. By analogy, Geppert and Zuntz (1888) defined 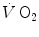 as the difference between inspired and expired oxygen flows, as follows:
as the difference between inspired and expired oxygen flows, as follows: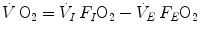
(2.4)
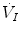 is the total inspired air flow—or more commonly inspiratory ventilation;
is the total inspired air flow—or more commonly inspiratory ventilation; 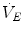 is the total expired air flow—or more commonly expiratory ventilation; and
is the total expired air flow—or more commonly expiratory ventilation; and 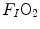 and
and 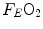 are the oxygen fractions in inspired and expired air, respectively. By definition, at steady state, Eqs. (2.3) and (2.4) have equal solutions.
are the oxygen fractions in inspired and expired air, respectively. By definition, at steady state, Eqs. (2.3) and (2.4) have equal solutions.Similar equations can be written to define 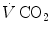 , by replacing its concentrations in blood—or its fractions in air—for the corresponding concentrations or fractions of oxygen. It is noteworthy, however, that the carbon dioxide concentration is higher in alveolar than in inspired air, and in mixed venous than in arterial blood, so that
, by replacing its concentrations in blood—or its fractions in air—for the corresponding concentrations or fractions of oxygen. It is noteworthy, however, that the carbon dioxide concentration is higher in alveolar than in inspired air, and in mixed venous than in arterial blood, so that 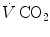 turns out negative. This being so, we have in blood:
turns out negative. This being so, we have in blood:
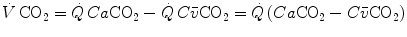
where 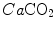 and
and 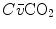 are the carbon dioxide concentrations, respectively, in arterial and mixed venous blood. It is of note that, in spite of its negative values, it soon became customary to express
are the carbon dioxide concentrations, respectively, in arterial and mixed venous blood. It is of note that, in spite of its negative values, it soon became customary to express 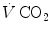 as absolute value, making abstraction of the sign.
as absolute value, making abstraction of the sign.
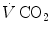 , by replacing its concentrations in blood—or its fractions in air—for the corresponding concentrations or fractions of oxygen. It is noteworthy, however, that the carbon dioxide concentration is higher in alveolar than in inspired air, and in mixed venous than in arterial blood, so that
, by replacing its concentrations in blood—or its fractions in air—for the corresponding concentrations or fractions of oxygen. It is noteworthy, however, that the carbon dioxide concentration is higher in alveolar than in inspired air, and in mixed venous than in arterial blood, so that 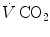 turns out negative. This being so, we have in blood:
turns out negative. This being so, we have in blood: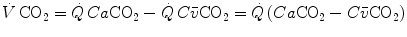
(2.5)
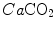 and
and 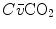 are the carbon dioxide concentrations, respectively, in arterial and mixed venous blood. It is of note that, in spite of its negative values, it soon became customary to express
are the carbon dioxide concentrations, respectively, in arterial and mixed venous blood. It is of note that, in spite of its negative values, it soon became customary to express 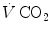 as absolute value, making abstraction of the sign.
as absolute value, making abstraction of the sign.Considering alveolar air, since in respiration physiology the carbon dioxide fraction in inspired air is considered nil, 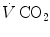 computation turns out simplified, as follows:
computation turns out simplified, as follows:
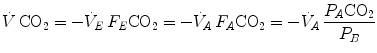
where 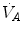 is alveolar ventilation,
is alveolar ventilation, 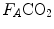 and
and 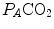 are the fraction and partial pressure, respectively, of carbon dioxide in alveolar air, and P B is the barometric pressure. Equation (2.6) demonstrates that at any given
are the fraction and partial pressure, respectively, of carbon dioxide in alveolar air, and P B is the barometric pressure. Equation (2.6) demonstrates that at any given 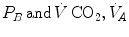 is inversely proportional to
is inversely proportional to 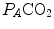 , whereas at any given
, whereas at any given 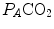 , it is directly proportional to
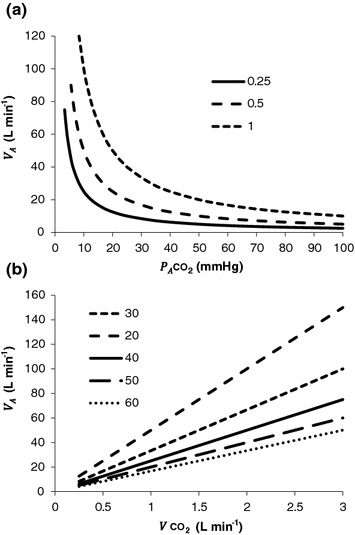
, it is directly proportional to 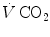 . The former relationship is reported in Fig. 2.2a. The latter relationship, which appears in Fig. 2.2b, is stable on a precise
. The former relationship is reported in Fig. 2.2a. The latter relationship, which appears in Fig. 2.2b, is stable on a precise 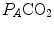 isopleth (that for
isopleth (that for 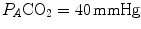 ) as long as a “true” steady state is maintained. This is so if there is no accumulation of lactate in blood. On ordinary non-athletic individuals, blood lactate accumulation starts having an impact on pH regulation at powers corresponding to some two-thirds of the maximal aerobic power. Although the exercise is still submaximal, above this power pH is not sufficiently buffered, hyperventilation superimposes and the
) as long as a “true” steady state is maintained. This is so if there is no accumulation of lactate in blood. On ordinary non-athletic individuals, blood lactate accumulation starts having an impact on pH regulation at powers corresponding to some two-thirds of the maximal aerobic power. Although the exercise is still submaximal, above this power pH is not sufficiently buffered, hyperventilation superimposes and the 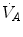 versus
versus 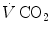 relationship bends upwards—higher
relationship bends upwards—higher 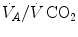 ratio and lower
ratio and lower 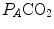 : the steady-state condition is broken. The origin of lactate in steady-state submaximal exercise is discussed in Chap. 3. It is nonetheless noteworthy already at this stage that the buffering of lactic acidosis in these circumstances has nothing to do with the concept, unfortunately deeply rooted in sport science, of shifting from aerobic to anaerobic metabolism.
: the steady-state condition is broken. The origin of lactate in steady-state submaximal exercise is discussed in Chap. 3. It is nonetheless noteworthy already at this stage that the buffering of lactic acidosis in these circumstances has nothing to do with the concept, unfortunately deeply rooted in sport science, of shifting from aerobic to anaerobic metabolism.
 computation turns out simplified, as follows:
computation turns out simplified, as follows: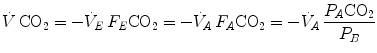
(2.6)
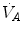 is alveolar ventilation,
is alveolar ventilation, 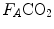 and
and 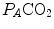 are the fraction and partial pressure, respectively, of carbon dioxide in alveolar air, and P B is the barometric pressure. Equation (2.6) demonstrates that at any given
are the fraction and partial pressure, respectively, of carbon dioxide in alveolar air, and P B is the barometric pressure. Equation (2.6) demonstrates that at any given 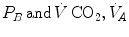 is inversely proportional to
is inversely proportional to 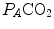 , whereas at any given
, whereas at any given 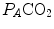 , it is directly proportional to
, it is directly proportional to 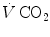 . The former relationship is reported in Fig. 2.2a. The latter relationship, which appears in Fig. 2.2b, is stable on a precise
. The former relationship is reported in Fig. 2.2a. The latter relationship, which appears in Fig. 2.2b, is stable on a precise 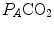 isopleth (that for
isopleth (that for 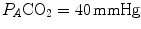 ) as long as a “true” steady state is maintained. This is so if there is no accumulation of lactate in blood. On ordinary non-athletic individuals, blood lactate accumulation starts having an impact on pH regulation at powers corresponding to some two-thirds of the maximal aerobic power. Although the exercise is still submaximal, above this power pH is not sufficiently buffered, hyperventilation superimposes and the
) as long as a “true” steady state is maintained. This is so if there is no accumulation of lactate in blood. On ordinary non-athletic individuals, blood lactate accumulation starts having an impact on pH regulation at powers corresponding to some two-thirds of the maximal aerobic power. Although the exercise is still submaximal, above this power pH is not sufficiently buffered, hyperventilation superimposes and the 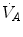 versus
versus 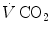 relationship bends upwards—higher
relationship bends upwards—higher 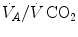 ratio and lower
ratio and lower 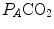 : the steady-state condition is broken. The origin of lactate in steady-state submaximal exercise is discussed in Chap. 3. It is nonetheless noteworthy already at this stage that the buffering of lactic acidosis in these circumstances has nothing to do with the concept, unfortunately deeply rooted in sport science, of shifting from aerobic to anaerobic metabolism.
: the steady-state condition is broken. The origin of lactate in steady-state submaximal exercise is discussed in Chap. 3. It is nonetheless noteworthy already at this stage that the buffering of lactic acidosis in these circumstances has nothing to do with the concept, unfortunately deeply rooted in sport science, of shifting from aerobic to anaerobic metabolism.
Fig. 2.2
Panel a Inverse relationship between alveolar ventilation (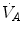 ) and alveolar partial pressure of carbon dioxide (
) and alveolar partial pressure of carbon dioxide (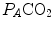 ) at the three indicated levels of steady-state carbon dioxide flow (
) at the three indicated levels of steady-state carbon dioxide flow (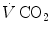 , in L min−1). Panel b Direct relationship between
, in L min−1). Panel b Direct relationship between 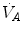 and
and 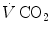 at the indicated levels of
at the indicated levels of 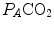 (in mmHg)
(in mmHg)
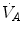 ) and alveolar partial pressure of carbon dioxide (
) and alveolar partial pressure of carbon dioxide (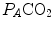 ) at the three indicated levels of steady-state carbon dioxide flow (
) at the three indicated levels of steady-state carbon dioxide flow (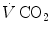 , in L min−1). Panel b Direct relationship between
, in L min−1). Panel b Direct relationship between 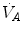 and
and 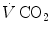 at the indicated levels of
at the indicated levels of 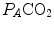 (in mmHg)
(in mmHg)If we express Eq. (2.4) in terms of partial pressures of alveolar gases, and we combine Eqs. (2.4) and (2.6) in the definition of RQ L , we obtain
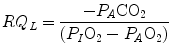
where 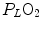 is the oxygen partial pressure in inspired air. The solution of Eq. (2.7) for
is the oxygen partial pressure in inspired air. The solution of Eq. (2.7) for 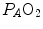 and
and 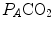 is
is
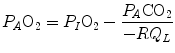
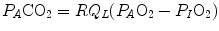
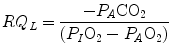
(2.7)
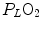 is the oxygen partial pressure in inspired air. The solution of Eq. (2.7) for
is the oxygen partial pressure in inspired air. The solution of Eq. (2.7) for 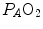 and
and 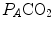 is
is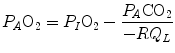
(2.8a)
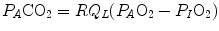
(2.8b)
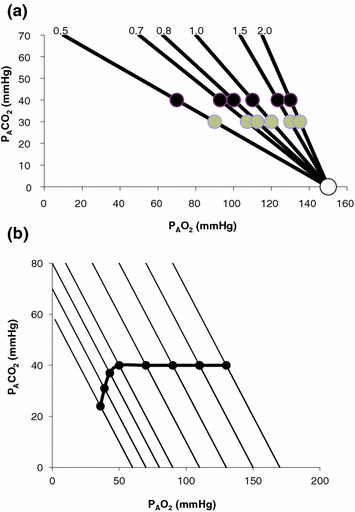
These equations are algebraic expressions of what is generally called the alveolar air equation. Its graphical representation is the O 2 –CO 2 diagram for alveolar gases (Rahn and Fenn 1955, see Fig. 2.3a), wherein we plot 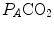 on the y-axis and
on the y-axis and 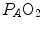 on the x-axis. Equation (2.8b) tells that there is a linear relationship between these two variables, with negative slope equal to −RQ L and x-axis intercept corresponding to the inspired air composition, with
on the x-axis. Equation (2.8b) tells that there is a linear relationship between these two variables, with negative slope equal to −RQ L and x-axis intercept corresponding to the inspired air composition, with 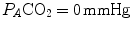 and
and 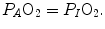 A family of isopleths for RQ L , all converging on a given inspired air composition (e.g.
A family of isopleths for RQ L , all converging on a given inspired air composition (e.g. 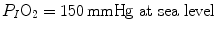 ), can be constructed. At steady state, the only possible combinations of
), can be constructed. At steady state, the only possible combinations of 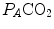 and
and 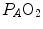 are those that lie on the RQ L isopleth corresponding to the actual RQ M . For any metabolic level below the critical power (see Chap. 5), the
are those that lie on the RQ L isopleth corresponding to the actual RQ M . For any metabolic level below the critical power (see Chap. 5), the 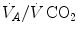 ratio is about 20 and the
ratio is about 20 and the 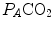 is about 40 mmHg, whereas the steady-state
is about 40 mmHg, whereas the steady-state 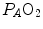 would vary depending on RQ L . Of course,
would vary depending on RQ L . Of course, 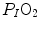 decreases in hypoxia and increases in hyperoxia, so that the inspired air point is accordingly shifted leftwards and rightwards, respectively, and so is the entire family of RQ L isopleths converging on it. In spite of this, as long as the metabolic rate stays below the critical power or the anaerobic threshold and there is no hyperventilation consequent to hypoxaemic stimulation of peripheral chemoreceptors, the
decreases in hypoxia and increases in hyperoxia, so that the inspired air point is accordingly shifted leftwards and rightwards, respectively, and so is the entire family of RQ L isopleths converging on it. In spite of this, as long as the metabolic rate stays below the critical power or the anaerobic threshold and there is no hyperventilation consequent to hypoxaemic stimulation of peripheral chemoreceptors, the 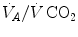 ratio remains about 20, and the steady-state
ratio remains about 20, and the steady-state 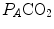 remains equal to 40 mmHg. Conversely, as hyperventilation appears, e.g., due to ventilatory response to hypoxaemia, the
remains equal to 40 mmHg. Conversely, as hyperventilation appears, e.g., due to ventilatory response to hypoxaemia, the 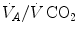 ratio increases and, since it is inversely proportional to
ratio increases and, since it is inversely proportional to 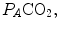 this decreases, moving downwards and rightwards along the corresponding RQ L isopleth, in the direction of the inspired air point. If at all
this decreases, moving downwards and rightwards along the corresponding RQ L isopleth, in the direction of the inspired air point. If at all 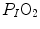 values we connect all the points representing the steady-state alveolar air composition, we obtain a curve like that reported in Fig. 2.3b, which is generally called the normal mean alveolar air curve.
values we connect all the points representing the steady-state alveolar air composition, we obtain a curve like that reported in Fig. 2.3b, which is generally called the normal mean alveolar air curve.
 on the y-axis and
on the y-axis and  on the x-axis. Equation (2.8b) tells that there is a linear relationship between these two variables, with negative slope equal to −RQ L and x-axis intercept corresponding to the inspired air composition, with
on the x-axis. Equation (2.8b) tells that there is a linear relationship between these two variables, with negative slope equal to −RQ L and x-axis intercept corresponding to the inspired air composition, with 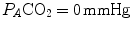 and
and 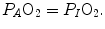 A family of isopleths for RQ L , all converging on a given inspired air composition (e.g.
A family of isopleths for RQ L , all converging on a given inspired air composition (e.g. 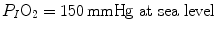 ), can be constructed. At steady state, the only possible combinations of
), can be constructed. At steady state, the only possible combinations of 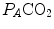 and
and 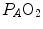 are those that lie on the RQ L isopleth corresponding to the actual RQ M . For any metabolic level below the critical power (see Chap. 5), the
are those that lie on the RQ L isopleth corresponding to the actual RQ M . For any metabolic level below the critical power (see Chap. 5), the 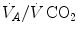 ratio is about 20 and the
ratio is about 20 and the 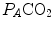 is about 40 mmHg, whereas the steady-state
is about 40 mmHg, whereas the steady-state 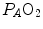 would vary depending on RQ L . Of course,
would vary depending on RQ L . Of course, 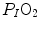 decreases in hypoxia and increases in hyperoxia, so that the inspired air point is accordingly shifted leftwards and rightwards, respectively, and so is the entire family of RQ L isopleths converging on it. In spite of this, as long as the metabolic rate stays below the critical power or the anaerobic threshold and there is no hyperventilation consequent to hypoxaemic stimulation of peripheral chemoreceptors, the
decreases in hypoxia and increases in hyperoxia, so that the inspired air point is accordingly shifted leftwards and rightwards, respectively, and so is the entire family of RQ L isopleths converging on it. In spite of this, as long as the metabolic rate stays below the critical power or the anaerobic threshold and there is no hyperventilation consequent to hypoxaemic stimulation of peripheral chemoreceptors, the 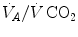 ratio remains about 20, and the steady-state
ratio remains about 20, and the steady-state 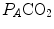 remains equal to 40 mmHg. Conversely, as hyperventilation appears, e.g., due to ventilatory response to hypoxaemia, the
remains equal to 40 mmHg. Conversely, as hyperventilation appears, e.g., due to ventilatory response to hypoxaemia, the 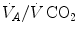 ratio increases and, since it is inversely proportional to
ratio increases and, since it is inversely proportional to 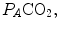 this decreases, moving downwards and rightwards along the corresponding RQ L isopleth, in the direction of the inspired air point. If at all
this decreases, moving downwards and rightwards along the corresponding RQ L isopleth, in the direction of the inspired air point. If at all 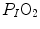 values we connect all the points representing the steady-state alveolar air composition, we obtain a curve like that reported in Fig. 2.3b, which is generally called the normal mean alveolar air curve.
values we connect all the points representing the steady-state alveolar air composition, we obtain a curve like that reported in Fig. 2.3b, which is generally called the normal mean alveolar air curve.
Fig. 2.3
Panel a An O2–CO2 diagram for alveolar air on which six isopleths of pulmonary respiratory quotient are indicated, all converging on the inspired air point corresponding to sea level (barometric pressure of 760 mmHg, white dot). On each isopleth, the points corresponding to alveolar air composition (black dots) and expired air composition (grey dots) are also shown. Panel b An O2–CO2 diagram for alveolar air, on which eight parallel isopleths (thin lines), corresponding to a pulmonary respiratory quotient of 1.0, are indicated, converging on different inspired air points. The lower is the inspired partial pressure of oxygen, the more the isopleth is displaced to the left. The corresponding alveolar air compositions are also shown (black dots) and connected by the alveolar air curve (thick black curve)
Equation (2.7) is a particular case in which nitrogen balance is nil, which is the case only when RQ L = −1. A resting human at steady state takes up 300 ml of oxygen per minute and gives out 250 ml of carbon dioxide per minute, on average, so that his RQ L is equal to −0.83. This means that inspired ventilation, or the air flow inside the alveoli, is higher than expired ventilation, because there is less carbon dioxide that is added to alveolar air than oxygen that is subtracted. Since pressure must equilibrate, this implies that inert gases, namely nitrogen, compensate for pressure differences. Thus, when RQ L ≠ −1, Eq. (2.7) becomes
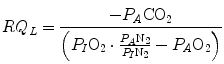
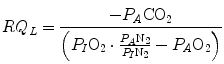
(2.9)
The two theoretical extremes for possible variations of RQ L are represented by RQ L = 0 and RQ L = −∞. The former is the case when 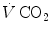 is nil, the latter when
is nil, the latter when 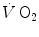 is nil. In the former case, since there is no carbon dioxide addition to the alveoli,
is nil. In the former case, since there is no carbon dioxide addition to the alveoli, 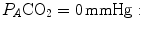 the corresponding isopleth for RQ L coincides with the x-axis. In the latter case, we have carbon dioxide addition to the alveoli in the absence of oxygen uptake: in this condition, there is a progressive dilution of oxygen and nitrogen in carbon dioxide, which goes on until carbon dioxide becomes the only alveolar gas. In this case,
the corresponding isopleth for RQ L coincides with the x-axis. In the latter case, we have carbon dioxide addition to the alveoli in the absence of oxygen uptake: in this condition, there is a progressive dilution of oxygen and nitrogen in carbon dioxide, which goes on until carbon dioxide becomes the only alveolar gas. In this case, 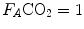 and
and 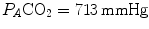 at sea level. As a consequence, the corresponding isopleth for RQ L does not coincide with the y-axis, but connects the point on the x-axis corresponding to inspired air composition to the point on the y-axis representing
at sea level. As a consequence, the corresponding isopleth for RQ L does not coincide with the y-axis, but connects the point on the x-axis corresponding to inspired air composition to the point on the y-axis representing 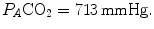
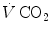 is nil, the latter when
is nil, the latter when 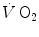 is nil. In the former case, since there is no carbon dioxide addition to the alveoli,
is nil. In the former case, since there is no carbon dioxide addition to the alveoli, 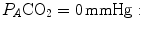 the corresponding isopleth for RQ L coincides with the x-axis. In the latter case, we have carbon dioxide addition to the alveoli in the absence of oxygen uptake: in this condition, there is a progressive dilution of oxygen and nitrogen in carbon dioxide, which goes on until carbon dioxide becomes the only alveolar gas. In this case,
the corresponding isopleth for RQ L coincides with the x-axis. In the latter case, we have carbon dioxide addition to the alveoli in the absence of oxygen uptake: in this condition, there is a progressive dilution of oxygen and nitrogen in carbon dioxide, which goes on until carbon dioxide becomes the only alveolar gas. In this case, 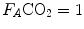 and
and 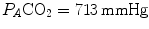 at sea level. As a consequence, the corresponding isopleth for RQ L does not coincide with the y-axis, but connects the point on the x-axis corresponding to inspired air composition to the point on the y-axis representing
at sea level. As a consequence, the corresponding isopleth for RQ L does not coincide with the y-axis, but connects the point on the x-axis corresponding to inspired air composition to the point on the y-axis representing 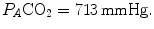
The Effects of Ventilation—Perfusion Heterogeneity
Although the O2–CO2 diagram was established for alveolar air, a similar diagram can be constructed for blood, starting from the computation of the respiratory quotient for blood (RQ B ) after Eqs. (2.3) and (2.5):
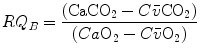
from which we obtain the following solution for  :
:
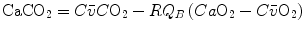
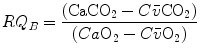
(2.10)
 :
: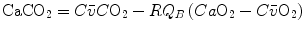
(2.11)
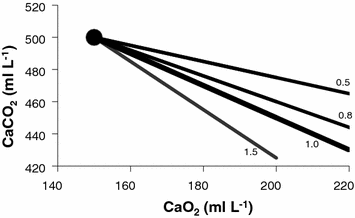
Equation (2.11), which is called the arterial blood equation, tells that, if we plot  as a function of
as a function of 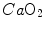 , we obtain a family of straight lines, with negative slopes equal to RQ B , which converge on a point, whose coordinates define the respiratory gas composition of mixed venous blood (Fig. 2.4). This means that, if no gas exchange occurs in the lungs, arterial blood would have the same oxygen and carbon dioxide concentrations as mixed venous blood.
, we obtain a family of straight lines, with negative slopes equal to RQ B , which converge on a point, whose coordinates define the respiratory gas composition of mixed venous blood (Fig. 2.4). This means that, if no gas exchange occurs in the lungs, arterial blood would have the same oxygen and carbon dioxide concentrations as mixed venous blood.
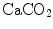 as a function of
as a function of 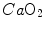 , we obtain a family of straight lines, with negative slopes equal to RQ B , which converge on a point, whose coordinates define the respiratory gas composition of mixed venous blood (Fig. 2.4). This means that, if no gas exchange occurs in the lungs, arterial blood would have the same oxygen and carbon dioxide concentrations as mixed venous blood.
, we obtain a family of straight lines, with negative slopes equal to RQ B , which converge on a point, whose coordinates define the respiratory gas composition of mixed venous blood (Fig. 2.4). This means that, if no gas exchange occurs in the lungs, arterial blood would have the same oxygen and carbon dioxide concentrations as mixed venous blood.
Fig. 2.4
Carbon dioxide concentration in arterial blood (Caco2) as a function of oxygen concentration of arterial blood (Cao2). The large dot refers to the concentrations incurring in mixed venous blood, where the isopleths for blood respiratory quotient (four of them are reported on the Figure, for the indicated values of respiratory quotient) converge
Respiratory gases move across the alveolar–capillary barrier by diffusion, driven by differences in partial pressure, not in concentration, which is dictated by the binding characteristics of respiratory gases to haemoglobin. So, it would have some interest expressing Eq. (2.11) in terms of partial pressures:
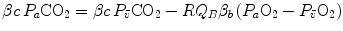
where constants β c and β b are the blood transport coefficients of carbon dioxide and oxygen, respectively, i.e. the slopes of the respective equilibrium curves with haemoglobin. The segment of the carbon dioxide equilibrium curve corresponding to the physiological range is practically linear, so that β c can be taken as invariant. In contrast, this is not so for β b : due to the shape of the oxygen equilibrium curve, β b is lower the higher is the 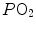 . An analytical solution of Eq. (2.12) thus requires an a priori solution of the oxygen equilibrium curve.
. An analytical solution of Eq. (2.12) thus requires an a priori solution of the oxygen equilibrium curve.
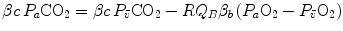
(2.12)
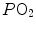 . An analytical solution of Eq. (2.12) thus requires an a priori solution of the oxygen equilibrium curve.
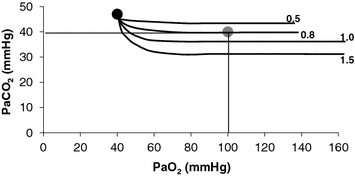
. An analytical solution of Eq. (2.12) thus requires an a priori solution of the oxygen equilibrium curve.All models describing the oxygen equilibrium curve are empirical, except Hill’s logarithmic model (Hill 1910; Ferretti 2012), whose theoretical basis, however, was confuted by the demonstration of the stereochemistry of haemoglobin (Perutz 1970). Although more precise descriptions of the oxygen equilibrium curve were published afterwards, Hill’s model has the great advantage of simplicity, while remaining accurate enough for the purpose of constructing an analytical solution of Eq. (2.12). This solution is presented in Fig. 2.5, which is generally called the O 2 –CO 2 diagram for blood gases (Rahn and Fenn 1955). This plot describes a family of curves, whose shape is dictated by the value that β b takes at any 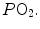 All these curves converge on a point, whose coordinates define the respiratory gas partial pressures of mixed venous blood.
All these curves converge on a point, whose coordinates define the respiratory gas partial pressures of mixed venous blood.
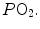 All these curves converge on a point, whose coordinates define the respiratory gas partial pressures of mixed venous blood.
All these curves converge on a point, whose coordinates define the respiratory gas partial pressures of mixed venous blood.
Fig. 2.5
An O2–CO2 diagram for blood on which four isopleths of blood respiratory quotient are indicated, all converging on the mixed venous blood point (black dot). The grey dot refers to the arterial blood gas composition of a man at rest (respiratory quotient of 0.8). Paco2 is the partial pressure of carbon dioxide in arterial blood; Paco2 is the partial pressure of oxygen in arterial blood
At steady state, RQ B = RQ L . If pulmonary gas exchange is complete, and equilibrium is attained on either side of the alveolar–capillary barrier, then arterial blood and alveolar air should have equal oxygen and carbon dioxide partial pressures. This coincidence of partial pressure values must then occur at the same respiratory quotient. Superposition on the same plot of the O2–CO2 diagrams for blood gases and for alveolar air (Fig. 2.6) clearly shows that this occurs at the crossing of two isopleths for a given RQ B and RQ L value (Farhi and Rahn 1955).
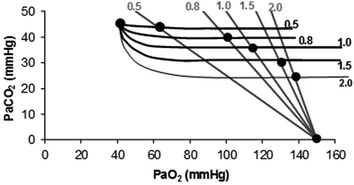

Fig. 2.6
Construction of the ideal air curve on an O2–CO2 diagram. The respiratory quotient isopleths for alveolar air are in grey, the corresponding isopleths for blood are in black. Dots are located at the crossing of each couple of isopleths and on the two extremes: the mixed venous blood composition (upper left dot) and the inspired air composition (lower right dot). The ideal air curve connects all these dots from mixed venous blood to inspired air
Figure 2.6 implies that (i) at any given respiratory quotient, only one combination of oxygen and carbon dioxide partial pressures is in fact possible, if we admit 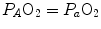 (ideal air, as defined by Farhi and Rahn 1955); (ii) this combination is comprised between two extremes, one represented by
(ideal air, as defined by Farhi and Rahn 1955); (ii) this combination is comprised between two extremes, one represented by 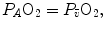 the other by
the other by 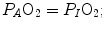 and (iii) connecting all possible combinations of oxygen and carbon dioxide partial pressures at steady state leads to the construction of a curve called the ideal air curve. It is of note that also the ideal air curve reflects the characteristics of the oxygen equilibrium curve: at high
and (iii) connecting all possible combinations of oxygen and carbon dioxide partial pressures at steady state leads to the construction of a curve called the ideal air curve. It is of note that also the ideal air curve reflects the characteristics of the oxygen equilibrium curve: at high 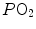 , when we operate on the flat part of the latter curve and we hyperventilate, relatively large drops of
, when we operate on the flat part of the latter curve and we hyperventilate, relatively large drops of 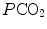 are associated with small increases in
are associated with small increases in 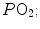 conversely, in the low
conversely, in the low 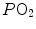 range, when we operate on the steep part of the oxygen equilibrium curve, relatively small increases of
range, when we operate on the steep part of the oxygen equilibrium curve, relatively small increases of 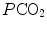 are associated with large drops in
are associated with large drops in 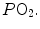
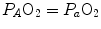 (ideal air, as defined by Farhi and Rahn 1955); (ii) this combination is comprised between two extremes, one represented by
(ideal air, as defined by Farhi and Rahn 1955); (ii) this combination is comprised between two extremes, one represented by 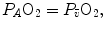 the other by
the other by 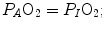 and (iii) connecting all possible combinations of oxygen and carbon dioxide partial pressures at steady state leads to the construction of a curve called the ideal air curve. It is of note that also the ideal air curve reflects the characteristics of the oxygen equilibrium curve: at high
and (iii) connecting all possible combinations of oxygen and carbon dioxide partial pressures at steady state leads to the construction of a curve called the ideal air curve. It is of note that also the ideal air curve reflects the characteristics of the oxygen equilibrium curve: at high 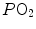 , when we operate on the flat part of the latter curve and we hyperventilate, relatively large drops of
, when we operate on the flat part of the latter curve and we hyperventilate, relatively large drops of 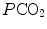 are associated with small increases in
are associated with small increases in 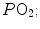 conversely, in the low
conversely, in the low 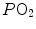 range, when we operate on the steep part of the oxygen equilibrium curve, relatively small increases of
range, when we operate on the steep part of the oxygen equilibrium curve, relatively small increases of 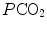 are associated with large drops in
are associated with large drops in 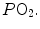
If we solve Eq. (2.6) for 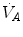 , we have
, we have
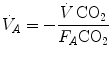
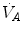 and
and 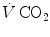 are not expressed in the same condition, since by convention the former is expressed in BTPS and the latter in STPD. Thus, if, after correcting for this inconsistency, we merge all constants and we transform
are not expressed in the same condition, since by convention the former is expressed in BTPS and the latter in STPD. Thus, if, after correcting for this inconsistency, we merge all constants and we transform 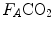 in
in 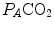 by means of Dalton’s law, we obtain
by means of Dalton’s law, we obtain
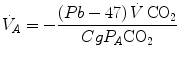
where Cg is the merged constant for STPD–BTPS transformation (0.863). If we replace 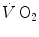 for
for 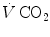 in Eq. (2.14), we get
in Eq. (2.14), we get
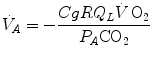
whence
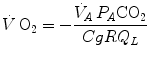
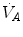 , we have
, we have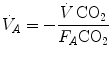
(2.13)
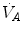 and
and 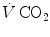 are not expressed in the same condition, since by convention the former is expressed in BTPS and the latter in STPD. Thus, if, after correcting for this inconsistency, we merge all constants and we transform
are not expressed in the same condition, since by convention the former is expressed in BTPS and the latter in STPD. Thus, if, after correcting for this inconsistency, we merge all constants and we transform 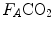 in
in 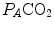 by means of Dalton’s law, we obtain
by means of Dalton’s law, we obtain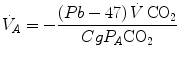
(2.14)
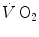 for
for 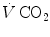 in Eq. (2.14), we get
in Eq. (2.14), we get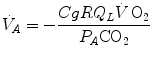
(2.15)
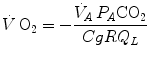
(2.16)
At steady state, since 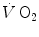 is the same at all levels along the respiratory system, Eqs. (2.16) and (2.3) must provide equivalent
is the same at all levels along the respiratory system, Eqs. (2.16) and (2.3) must provide equivalent 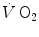 values, so that, when we take their ratio, we have
values, so that, when we take their ratio, we have
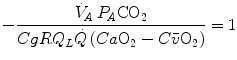
whence, after rearrangement, we get
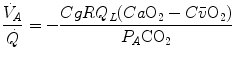
which Hermann Rahn and Wallace Fenn called the ventilation–perfusion equation (Rahn and Fenn 1955). Equation (2.18) tells that at steady state, in any given segment of the lungs, the 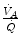 ratio is directly proportional to −RQ L and to
ratio is directly proportional to −RQ L and to 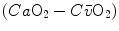 and inversely proportional to
and inversely proportional to 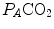 . As a consequence, on the ideal air curve (Fig. 2.6), each point corresponds not only to a specific RQ L value, but also to a unique value of
. As a consequence, on the ideal air curve (Fig. 2.6), each point corresponds not only to a specific RQ L value, but also to a unique value of 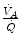 ratio, which is lower the closer is RQ L to zero. Moreover, if we look at the extremes of the ideal air curve, we note that, when
ratio, which is lower the closer is RQ L to zero. Moreover, if we look at the extremes of the ideal air curve, we note that, when 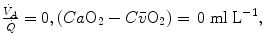 so that the blood that leaves alveolar capillaries in which
so that the blood that leaves alveolar capillaries in which 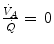 has the same composition of mixed venous blood. On the other side, whenever
has the same composition of mixed venous blood. On the other side, whenever 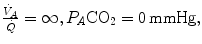 so that the composition of alveolar air becomes equal to that of inspired air.
so that the composition of alveolar air becomes equal to that of inspired air.
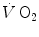 is the same at all levels along the respiratory system, Eqs. (2.16) and (2.3) must provide equivalent
is the same at all levels along the respiratory system, Eqs. (2.16) and (2.3) must provide equivalent 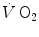 values, so that, when we take their ratio, we have
values, so that, when we take their ratio, we have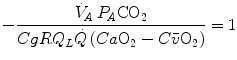
(2.17)
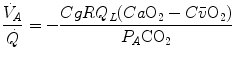
(2.18)
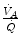 ratio is directly proportional to −RQ L and to
ratio is directly proportional to −RQ L and to 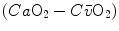 and inversely proportional to
and inversely proportional to 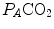 . As a consequence, on the ideal air curve (Fig. 2.6), each point corresponds not only to a specific RQ L value, but also to a unique value of
. As a consequence, on the ideal air curve (Fig. 2.6), each point corresponds not only to a specific RQ L value, but also to a unique value of 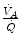 ratio, which is lower the closer is RQ L to zero. Moreover, if we look at the extremes of the ideal air curve, we note that, when
ratio, which is lower the closer is RQ L to zero. Moreover, if we look at the extremes of the ideal air curve, we note that, when 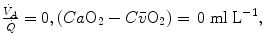 so that the blood that leaves alveolar capillaries in which
so that the blood that leaves alveolar capillaries in which 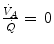 has the same composition of mixed venous blood. On the other side, whenever
has the same composition of mixed venous blood. On the other side, whenever 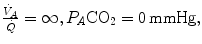 so that the composition of alveolar air becomes equal to that of inspired air.
so that the composition of alveolar air becomes equal to that of inspired air.During light exercise at steady state, as compared to rest, 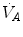 increases in direct proportion to
increases in direct proportion to 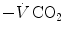 , whereas the increase of
, whereas the increase of 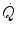 is less. As a consequence, the
is less. As a consequence, the 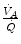 ratio grows. Since in this case
ratio grows. Since in this case 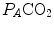 does not move from its controlled value of 40 mmHg, most of the increase of the
does not move from its controlled value of 40 mmHg, most of the increase of the 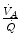 ratio, apart from the changes of RQ M due to the progressively greater fraction of aerobic energy derived from glycogen oxidation (see Chap. 1), is due to the widening of
ratio, apart from the changes of RQ M due to the progressively greater fraction of aerobic energy derived from glycogen oxidation (see Chap. 1), is due to the widening of 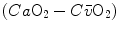 . However, as long as we operate on the flat part of the oxygen equilibrium curve,
. However, as long as we operate on the flat part of the oxygen equilibrium curve, 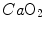 does not vary, so that an increase of
does not vary, so that an increase of 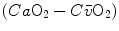 can be sustained only by a fall of
can be sustained only by a fall of 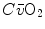 . This is inevitably associated with an increase in
. This is inevitably associated with an increase in 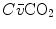 , so it moves the mixed venous point of an O2–CO2 diagram upwards and leftwards. Since the inspired air point is unchanged as long as we breathe air at sea level, the shape of the ideal air curve is modified at exercise with respect to rest, as represented in Fig. 2.7.
, so it moves the mixed venous point of an O2–CO2 diagram upwards and leftwards. Since the inspired air point is unchanged as long as we breathe air at sea level, the shape of the ideal air curve is modified at exercise with respect to rest, as represented in Fig. 2.7.
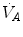 increases in direct proportion to
increases in direct proportion to 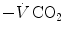 , whereas the increase of
, whereas the increase of 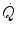 is less. As a consequence, the
is less. As a consequence, the 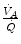 ratio grows. Since in this case
ratio grows. Since in this case 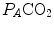 does not move from its controlled value of 40 mmHg, most of the increase of the
does not move from its controlled value of 40 mmHg, most of the increase of the 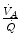 ratio, apart from the changes of RQ M due to the progressively greater fraction of aerobic energy derived from glycogen oxidation (see Chap. 1), is due to the widening of
ratio, apart from the changes of RQ M due to the progressively greater fraction of aerobic energy derived from glycogen oxidation (see Chap. 1), is due to the widening of 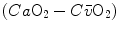 . However, as long as we operate on the flat part of the oxygen equilibrium curve,
. However, as long as we operate on the flat part of the oxygen equilibrium curve, 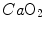 does not vary, so that an increase of
does not vary, so that an increase of 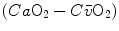 can be sustained only by a fall of
can be sustained only by a fall of 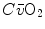 . This is inevitably associated with an increase in
. This is inevitably associated with an increase in 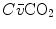 , so it moves the mixed venous point of an O2–CO2 diagram upwards and leftwards. Since the inspired air point is unchanged as long as we breathe air at sea level, the shape of the ideal air curve is modified at exercise with respect to rest, as represented in Fig. 2.7.
, so it moves the mixed venous point of an O2–CO2 diagram upwards and leftwards. Since the inspired air point is unchanged as long as we breathe air at sea level, the shape of the ideal air curve is modified at exercise with respect to rest, as represented in Fig. 2.7.
Fig. 2.7
Displacement of ideal air curve at exercise with respect to rest. The changes in the partial pressures of respiratory gases at exercise move the mixed venous point upwards and leftwards, without changes in inspired air composition. The ideal air curve is modified accordingly. Note that the ideal alveolar air composition is affected also by the change of the metabolic respiratory quotient during exercise
The direct proportionality between 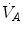 and
and 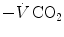 implies invariance of their ratio, and thus of
implies invariance of their ratio, and thus of 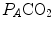 . The tight matching between
. The tight matching between 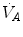 and
and 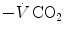 is the result of a fine regulation, mostly centred on the activity of the central chemoreceptors and the characteristics of their response. This equilibrium is broken in case of hyperventilation, when
is the result of a fine regulation, mostly centred on the activity of the central chemoreceptors and the characteristics of their response. This equilibrium is broken in case of hyperventilation, when 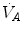 increases in the absence of a proportional increase of metabolism, i.e. of
increases in the absence of a proportional increase of metabolism, i.e. of 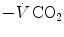 , so that their ratio goes up: in this case, the new steady state is attained at a lower value of
, so that their ratio goes up: in this case, the new steady state is attained at a lower value of 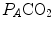 . This is so, e.g. at high altitude, due to hypoxic stimulation of peripheral chemoreceptors, or in case of pathological disturbances of
. This is so, e.g. at high altitude, due to hypoxic stimulation of peripheral chemoreceptors, or in case of pathological disturbances of 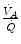 ratio heterogeneity in the lungs. The reverse takes place when hypoventilation occurs, as in case of respiratory failure or of paralysis of the respiratory centres.
ratio heterogeneity in the lungs. The reverse takes place when hypoventilation occurs, as in case of respiratory failure or of paralysis of the respiratory centres.
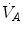 and
and 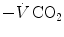 implies invariance of their ratio, and thus of
implies invariance of their ratio, and thus of 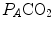 . The tight matching between
. The tight matching between 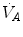 and
and 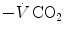 is the result of a fine regulation, mostly centred on the activity of the central chemoreceptors and the characteristics of their response. This equilibrium is broken in case of hyperventilation, when
is the result of a fine regulation, mostly centred on the activity of the central chemoreceptors and the characteristics of their response. This equilibrium is broken in case of hyperventilation, when 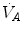 increases in the absence of a proportional increase of metabolism, i.e. of
increases in the absence of a proportional increase of metabolism, i.e. of 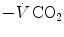 , so that their ratio goes up: in this case, the new steady state is attained at a lower value of
, so that their ratio goes up: in this case, the new steady state is attained at a lower value of 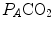 . This is so, e.g. at high altitude, due to hypoxic stimulation of peripheral chemoreceptors, or in case of pathological disturbances of
. This is so, e.g. at high altitude, due to hypoxic stimulation of peripheral chemoreceptors, or in case of pathological disturbances of 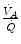 ratio heterogeneity in the lungs. The reverse takes place when hypoventilation occurs, as in case of respiratory failure or of paralysis of the respiratory centres.
ratio heterogeneity in the lungs. The reverse takes place when hypoventilation occurs, as in case of respiratory failure or of paralysis of the respiratory centres.Equilibration between alveolar air and arterial blood is the main assumption behind the ideal air curve. This equilibration in normoxia occurs indeed in each pulmonary capillary which is in contact with an alveolus, provided the contact time between alveolar air and capillary blood is long enough. According to Wagner and West (1972), at rest, full equilibration between the two sides of the alveolar–capillary barrier is attained when the blood has completed about one-third of the capillary length, this fraction increasing at exercise due to higher blood flow. In spite of this, 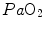 is lower than
is lower than 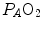 in real lungs. This is a consequence of the combined effect of the heterogeneity of
in real lungs. This is a consequence of the combined effect of the heterogeneity of 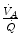 distribution in the lungs and of the shape of the oxygen equilibrium curve. Alveoli perfused by capillaries in a lung segment with elevated
distribution in the lungs and of the shape of the oxygen equilibrium curve. Alveoli perfused by capillaries in a lung segment with elevated 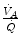 ratio are characterized by high
ratio are characterized by high 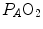 and end-capillary
and end-capillary 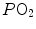 values, in perfect equilibrium; on the other side, alveoli perfused by capillaries in a lung segment with low
values, in perfect equilibrium; on the other side, alveoli perfused by capillaries in a lung segment with low 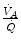 ratio are characterized by low
ratio are characterized by low 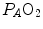 and end-capillary
and end-capillary 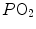 values, again in perfect equilibrium. One would expect that the former capillaries would compensate for the latter capillaries, when capillary blood is mixed to form arterial blood in the pulmonary vein, pretty much as air coming from different alveoli does in the trachea, where it forms the mean alveolar air that is analysed at the end of a prolonged expiration. This averaging of blood coming from different capillaries occurs indeed; however, in contrast with alveolar air, it is the binding of oxygen to haemoglobin with allosteric kinetics that dictates blood oxygen concentration at any
values, again in perfect equilibrium. One would expect that the former capillaries would compensate for the latter capillaries, when capillary blood is mixed to form arterial blood in the pulmonary vein, pretty much as air coming from different alveoli does in the trachea, where it forms the mean alveolar air that is analysed at the end of a prolonged expiration. This averaging of blood coming from different capillaries occurs indeed; however, in contrast with alveolar air, it is the binding of oxygen to haemoglobin with allosteric kinetics that dictates blood oxygen concentration at any 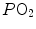 , through an oxygen equilibrium curve that is sigmoidal. On one side, the blood draining from capillaries with low
, through an oxygen equilibrium curve that is sigmoidal. On one side, the blood draining from capillaries with low 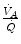 ratio has a decreased end-capillary
ratio has a decreased end-capillary 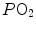 , close to the steep part of the oxygen equilibrium curve, so that their oxygen concentration is reduced indeed. On the other side, the blood draining from capillaries with high
, close to the steep part of the oxygen equilibrium curve, so that their oxygen concentration is reduced indeed. On the other side, the blood draining from capillaries with high 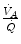 ratio has an increased end-capillary
ratio has an increased end-capillary 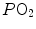 , located on the flat part of the oxygen equilibrium curve, so that their oxygen concentration is not or minimally increased, which prevents them from compensating for the effect of the capillaries with low
, located on the flat part of the oxygen equilibrium curve, so that their oxygen concentration is not or minimally increased, which prevents them from compensating for the effect of the capillaries with low 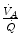 ratio. This is the cause of the reduction of
ratio. This is the cause of the reduction of 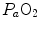 with respect to
with respect to 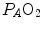 and of the appearance of the alveolar–arterial pressure difference. This state of things is illustrated in Fig. 2.8. The same is not the case for carbon dioxide, because of the steepness of a linear carbon dioxide equilibrium curve in the physiological range.
and of the appearance of the alveolar–arterial pressure difference. This state of things is illustrated in Fig. 2.8. The same is not the case for carbon dioxide, because of the steepness of a linear carbon dioxide equilibrium curve in the physiological range.
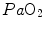 is lower than
is lower than 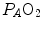 in real lungs. This is a consequence of the combined effect of the heterogeneity of
in real lungs. This is a consequence of the combined effect of the heterogeneity of 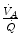 distribution in the lungs and of the shape of the oxygen equilibrium curve. Alveoli perfused by capillaries in a lung segment with elevated
distribution in the lungs and of the shape of the oxygen equilibrium curve. Alveoli perfused by capillaries in a lung segment with elevated 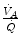 ratio are characterized by high
ratio are characterized by high 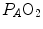 and end-capillary
and end-capillary 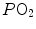 values, in perfect equilibrium; on the other side, alveoli perfused by capillaries in a lung segment with low
values, in perfect equilibrium; on the other side, alveoli perfused by capillaries in a lung segment with low 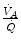 ratio are characterized by low
ratio are characterized by low 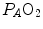 and end-capillary
and end-capillary 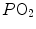 values, again in perfect equilibrium. One would expect that the former capillaries would compensate for the latter capillaries, when capillary blood is mixed to form arterial blood in the pulmonary vein, pretty much as air coming from different alveoli does in the trachea, where it forms the mean alveolar air that is analysed at the end of a prolonged expiration. This averaging of blood coming from different capillaries occurs indeed; however, in contrast with alveolar air, it is the binding of oxygen to haemoglobin with allosteric kinetics that dictates blood oxygen concentration at any
values, again in perfect equilibrium. One would expect that the former capillaries would compensate for the latter capillaries, when capillary blood is mixed to form arterial blood in the pulmonary vein, pretty much as air coming from different alveoli does in the trachea, where it forms the mean alveolar air that is analysed at the end of a prolonged expiration. This averaging of blood coming from different capillaries occurs indeed; however, in contrast with alveolar air, it is the binding of oxygen to haemoglobin with allosteric kinetics that dictates blood oxygen concentration at any 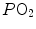 , through an oxygen equilibrium curve that is sigmoidal. On one side, the blood draining from capillaries with low
, through an oxygen equilibrium curve that is sigmoidal. On one side, the blood draining from capillaries with low 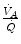 ratio has a decreased end-capillary
ratio has a decreased end-capillary 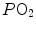 , close to the steep part of the oxygen equilibrium curve, so that their oxygen concentration is reduced indeed. On the other side, the blood draining from capillaries with high
, close to the steep part of the oxygen equilibrium curve, so that their oxygen concentration is reduced indeed. On the other side, the blood draining from capillaries with high 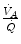 ratio has an increased end-capillary
ratio has an increased end-capillary 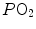 , located on the flat part of the oxygen equilibrium curve, so that their oxygen concentration is not or minimally increased, which prevents them from compensating for the effect of the capillaries with low
, located on the flat part of the oxygen equilibrium curve, so that their oxygen concentration is not or minimally increased, which prevents them from compensating for the effect of the capillaries with low 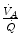 ratio. This is the cause of the reduction of
ratio. This is the cause of the reduction of 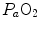 with respect to
with respect to 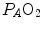 and of the appearance of the alveolar–arterial pressure difference. This state of things is illustrated in Fig. 2.8. The same is not the case for carbon dioxide, because of the steepness of a linear carbon dioxide equilibrium curve in the physiological range.
and of the appearance of the alveolar–arterial pressure difference. This state of things is illustrated in Fig. 2.8. The same is not the case for carbon dioxide, because of the steepness of a linear carbon dioxide equilibrium curve in the physiological range.
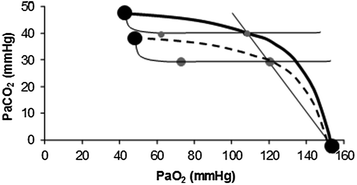
Fig. 2.8
Identification of the alveolar–arterial oxygen pressure difference on the O2–CO2 diagram as the horizontal distance between the two grey dots on a given respiratory quotient isopleth for blood. The effects of hyperventilation (dashed curve) are also shown. Note that hyperventilation does not change the alveolar–arterial oxygen pressure difference
Diffusion–Perfusion Interaction in Alveolar–Capillary Gas Transfer
Alveolar–capillary gas transfer is the result of two interrelated mechanisms: diffusion across the alveolar–capillary barrier, and lung capillary perfusion. At steady state, the flow of gas (e.g. oxygen) leaving the lungs through capillary blood must be equal to the flow of gas that crosses the alveolar–capillary barrier. This can be described with a very simple model of a meta-capillary with steady blood flow, which is in contact for its entire length with a meta-alveolus through a thin, homogeneous membrane. This is tantamount to imagine the mean pulmonary blood flow in contact with the mean alveolar air, with oxygen diffusing across a mean alveolar–capillary barrier. If this is so, the gas flow 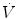 across the membrane of given surface area A and thickness L is directly proportional to the pressure gradient across that membrane:
across the membrane of given surface area A and thickness L is directly proportional to the pressure gradient across that membrane:
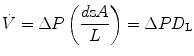
where d and s are the diffusion and solubility constants of the gas at stake in the barrier, and D l is the lumped constant called lung diffusing capacity. ∆P is the effective pressure gradient, i.e. the difference between 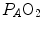 and the pressure existing in the capillary at a given distance δ from the venous entrance [P c (δ)]. For the specific case of oxygen, the diffusive
and the pressure existing in the capillary at a given distance δ from the venous entrance [P c (δ)]. For the specific case of oxygen, the diffusive 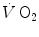 across the barrier at any distance δ is thus equal to
across the barrier at any distance δ is thus equal to
![$$ d\dot{V}\,{\text{O}}_{2} = [P_{A} {\text{O}}_{2} - P_{c} {\text{O}}_{2} ({\updelta})]D_{\text{L}} $$](/wp-content/uploads/2016/09/A322139_1_En_2_Chapter_Equ21.gif)
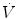 across the membrane of given surface area A and thickness L is directly proportional to the pressure gradient across that membrane:
across the membrane of given surface area A and thickness L is directly proportional to the pressure gradient across that membrane: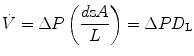
(2.19)
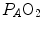 and the pressure existing in the capillary at a given distance δ from the venous entrance [P c (δ)]. For the specific case of oxygen, the diffusive
and the pressure existing in the capillary at a given distance δ from the venous entrance [P c (δ)]. For the specific case of oxygen, the diffusive 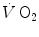 across the barrier at any distance δ is thus equal to
across the barrier at any distance δ is thus equal to![$$ d\dot{V}\,{\text{O}}_{2} = [P_{A} {\text{O}}_{2} - P_{c} {\text{O}}_{2} ({\updelta})]D_{\text{L}} $$](/wp-content/uploads/2016/09/A322139_1_En_2_Chapter_Equ21.gif)
(2.20)
The infinitesimal 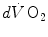 across the barrier progressively raises the
across the barrier progressively raises the 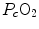 at δ from the venous to the arterial side in inverse proportion to blood flow
at δ from the venous to the arterial side in inverse proportion to blood flow 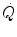 and to the gas transport coefficient in blood (for oxygen, β b )
and to the gas transport coefficient in blood (for oxygen, β b )
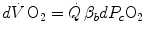
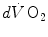 across the barrier progressively raises the
across the barrier progressively raises the 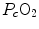 at δ from the venous to the arterial side in inverse proportion to blood flow
at δ from the venous to the arterial side in inverse proportion to blood flow 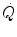 and to the gas transport coefficient in blood (for oxygen, β b )
and to the gas transport coefficient in blood (for oxygen, β b )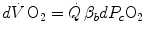
(2.21)
For inert gases, β is a constant that is independent of the gas pressure. For oxygen, β b does depend on 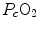 , because of the allosteric characteristics of oxygen binding to haemoglobin. If for simplification we assume β b invariant, i.e. we take the average slope of the oxygen equilibrium curve as the invariant β b value, the rate of increase of
, because of the allosteric characteristics of oxygen binding to haemoglobin. If for simplification we assume β b invariant, i.e. we take the average slope of the oxygen equilibrium curve as the invariant β b value, the rate of increase of 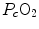 along the capillary tends to an asymptote corresponding to
along the capillary tends to an asymptote corresponding to 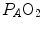 (Krogh 1922). On this basis, at steady state, combination of Eqs. (2.20) and (2.21) and subsequent integration along the capillary length yields
(Krogh 1922). On this basis, at steady state, combination of Eqs. (2.20) and (2.21) and subsequent integration along the capillary length yields
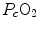 , because of the allosteric characteristics of oxygen binding to haemoglobin. If for simplification we assume β b invariant, i.e. we take the average slope of the oxygen equilibrium curve as the invariant β b value, the rate of increase of
, because of the allosteric characteristics of oxygen binding to haemoglobin. If for simplification we assume β b invariant, i.e. we take the average slope of the oxygen equilibrium curve as the invariant β b value, the rate of increase of 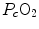 along the capillary tends to an asymptote corresponding to
along the capillary tends to an asymptote corresponding to 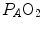 (Krogh 1922). On this basis, at steady state, combination of Eqs. (2.20) and (2.21) and subsequent integration along the capillary length yields
(Krogh 1922). On this basis, at steady state, combination of Eqs. (2.20) and (2.21) and subsequent integration along the capillary length yields