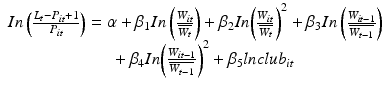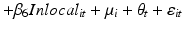A Panel Analysis of the Relationship Between Club Performance and Wages

(9.1)

where L is the number of clubs participating in the J-League, 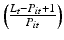$\left(\frac{L_t-{P}_{it}+1}{P_{it}}\right)$ represents the log odds of the league position, and 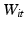${W}_{it}$ is the wage expenditure of club i in season t. 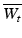$\overline{W_t}$ gives the average wage expenditure in season t. P is the league position.

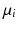$\mu_i$ indicates club i’s fixed effect and 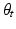${\theta}_t$ indicates the time effect of season t. This is assumed to depend on a club specific fixed effect, which may reflect the history of the club, time effect, and relative wage achieved in the season.

The empirical analogue of Eq. (9.1) is

$\begin{array}{l} In\left(\frac{L_t-{P}_{it}+1}{P_{it}}\right)=\alpha+{\beta}_1 In\left(\frac{W_{it}}{\overline{W_t}}\right)+{\beta}_2 In{\left(\frac{W_{it}}{\overline{W_t}}\right)}^2+{\beta}_3 In\left(\frac{W_{it-1}}{\overline{W_{t-1}}}\right)\\ {} \qquad \qquad \qquad+{\beta}_4 In{\left(\frac{W_{it-1}}{\overline{W_{t-1}}}\right)}^2+{\beta}_5 lnclu{b}_{it}\end{array}$

$+{\beta}_6 Inloca{l}_{it}+{\mu}_i+{\theta}_t+{\varepsilon}_{it}$

(9.2)

The odds transformation works particularly well because its implication is that league positions rise when the club’s wage is above the league average and fall when the club’s wage is below the league average.

Previous studies assumed that there was a linear relationship between a club’s performance and its wages. In this study, because there may be a non-linear relationship between the club’s performance and wages, we introduce a square term for the variable of the wages.³

In addition, we introduce wages of the last season to assess whether they affect the ranking of the current season. Furthermore, because we assume that the performance of the club is related to the competency of its supervision, we introduce the labor costs of managers and players.

We estimate two types of models: a two-way effects model and a fixed effects model. After conducting tests of the estimation equations, we select the most appropriate model.

9.3 Results

9.3.1 Estimation Results

We report our results in Table 9.1. We utilized two versions of the model, the fixed effects estimator (Garcia-del-Barrio and Szymanski 2006) and the two-way effects estimator (Pollard 1986). On the basis of the estimation results, we performed two tests for the formulation of the model. First, the F-test assesses whether the pooling estimate model or the fixed effects model is appropriate. Second, the Hausman test assesses whether the random effects model or the fixed effects model is appropriate.

Table 9.1

League position and wage

	(Garcia-del-Barrio and Szymanski 2006) fixed effects	(Pollard 1986) two-way fixed effects
LogRank(−1)	−0.131(−0.98)	−0.120(−0.90)
Relative wage	0.245(0.50)
Relative wage(square)	−0.462*(−1.96)	−0.405*(−1.72)
Relative wage(−1) (square)	0.256(1.14)	0.299(1.29)
Spectator per game	1.621***(3.74)	1.797***(6.19)
Average age		−1.594(−0.74)
Watching Frequency	−0.509(−1.32)	−0.498(−1.32)
prefectural income per capita	−3.284**(−2.45)
Hausman test	58.826
Hausman test	<7>
AIC	2.007	2.029
Durbin-Watson Stat	2.432	2.326
Adj R²	0.854	0.852
No obs.	111	111

Note 1: *p < .1, **p < .05, ***p < .01

Note 2: Parentheses in the parameter indicates the t-value

The results of the F-test show that the F value of estimation model (Garcia-del-Barrio and Szymanski 2006) is large. We adopted the fixed effects model because the test reject the null hypothesis that the pooling estimate model is correct at the 1 % significance level. In addition, the results of the Hausman test provide a P-value of the statistic of 0 %. The result of Hausman test shows that fixed effects model is more desirable than random effects model.

Thus, from the results of the Hausman test and F-test, the most desirable model is the fixed effects model.

Since the problem of non-uniform dispersion is present in general in the panel data, bias remains in the estimated parameters without a robust estimation of estimation error (Kitamura 2005). Therefore, we modify the standard error by modifying the simultaneous correlation error in the estimation results in this study.

In response to the test results for the formulation of the estimation model (Garcia-del-Barrio and Szymanski 2006), we discuss the significance of the parameters of it. From the estimation results using all variables, we sequentially remove the insignificant variables from the estimated results of estimation model (Garcia-del-Barrio and Szymanski 2006). Only the variable of average age was removed. The t-value of prefectural income per capita, per game admission, and the number of the square of the relative wage are significant. However, the t-value of the log rank of the previous season, relative wage, the square of the previous relative wage, and spectator frequency are not significant.

Estimation model (Pollard 1986) assumes both a time effect and a fixed effect. We performed the Redundant tests to select the desirable model. We used three models. These models were (1) a model that has fixed effects, (2) a model that has time effects and (3) a model that has fixed effects and time effects.

The results of the Redundant test in estimation model (Pollard 1986) show that the null hypotheses of the following three models are rejected at the 1 %, 5 %, and 1 % significance levels, respectively:

(1)

excluding the fixed effects of the cross-section

(2)

excluding the fixed effect of time

(3)

excluding the fixed effect of time and the cross-section.

Therefore, we created: (1) a fixed effects model, (2) a time fixed effects model, and (3) a two-way fixed effects model. We then conducted a comparison of the value of Akaike’s Information Criterion (AIC) for each model.

We selected the two-way fixed effects model because its AIC was the smallest. As a result, the t-value of the square of the relative wage and spectators per game are significant, but the t-value of the log rank of the previous season, the square of the previous relative wage, average age, and spectator frequency are not significant.

In estimation models (Garcia-del-Barrio and Szymanski 2006) and (Pollard 1986), we find that the coefficient of per game average attendance and the square of the relative wage are significant and these variables are stable. In addition, estimation model (Garcia-del-Barrio and Szymanski 2006) is lower when comparing AIC. Thus, we use estimation model (Garcia-del-Barrio and Szymanski 2006) to interpret the estimation results.

9.3.2 Interpretation of the Estimation Results

As a result of the Hausman test, we selected the fixed effects model for the estimation model (Garcia-del-Barrio and Szymanski 2006). This implies that there are individual effects that impact on the club’s rank and these are fixed effects. It means that the club’s fixed effect is larger and that the club has enjoyed a better performance with the same wages. Those clubs likely have a better team management through the employment of excellent supervisors of inexpensive players.

In addition, increases in per game attendance and wages significantly increase the ranking of the club. Spectators provide social support for the players. Schwartz and Barsky (1977) find that spectators directly affect the performance of teams by cheering them on. Pollard (1986) refers to indirect effects in that the pressure of spectators makes referees more likely to make favorable decisions for the home team, although such decisions are likely unconscious. Thus, social support from spectators increases the performance of clubs.

We interpret as follows the estimation results that per capita prefectural income significantly negatively affects performance of clubs. Tickets for soccer games at stadiums are inferior goods, in that demand for tickets is reduced as income increases. Inferior goods are goods that decrease in demand when consumer income rises (or rises in demand when consumer income decreases.) On the other hand, normal goods are those for which consumers’ demand increases when their income increases.

Only gold members can continue reading. Log In or Register to continue